Расчет раствора на фундамент: Калькулятор ленточного фундамента

Калькулятор ленточного фундамента. Расчет материалов.

Поиск для:

---

Ленточный фундамент представляет собой замкнутый контур (ленту) — полосу из железобетона, укладываемую под всеми несущими стенами здания и распределяющую вес здания по всему своему периметру. Таким образом, оказывая сопротивление силам выпучивания почвы, избегая проседания и перекоса здания.

Устройство монолитного ленточного фундамента предполагает вязку арматурного каркаса и заливку его бетоном на самом строительном объекте, за счет чего и достигается целостность, или неразрывность — монолитность основания фундамента.

Калькулятор ленточного фундамента помогает рассчитать:

• Площадь основания фундамента
• Количество бетона для фундамента и плит перекрытия или заливки пола подвала
• Арматура — количество арматуры, автоматический расчет ее веса, исходя из ее длины и диаметра
• Площадь опалубки и количество пиломатериала в кубометрах и в штуках
• Площадь всех поверхностей  и боковых поверхностей и основания
• Расчет стоимости стройматериалов фундамента.

Калькулятор ленточного фундамента

Тип фундамента
вариант 1	вариант 5
вариант 2	вариант 6
вариант 3	вариант 7
вариант 4	вариант 8
Размеры фундамента
Ширина, мм.
Длина, мм.
Высота, мм.
Толщина, мм.
Размер, мм.
Арматура
Горизонтальные ряды	01234567 8910
Вертикальные стержни	012345
Соединительные стержни	012345
Шаг
Диаметр арматуры	68101214161820222528
Опалубка
Толщина доски для опалубки, мм.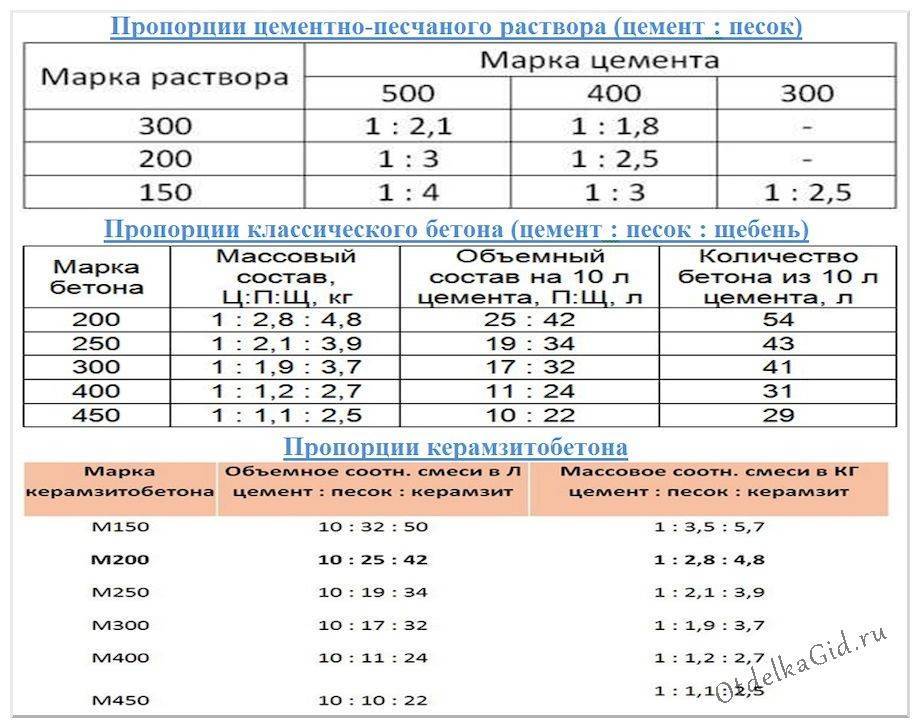
Длина доски, мм.
Ширина доски, мм.
Состав бетона
Вес одного мешка, кг.
Мешков на 1 кубометр бетона
Пропорции бетона по весу
Цемент
Песок
Щебень
Стоимость строительных материалов
Цемент (за мешок)
Песок (за 1 тонну)
Щебень (за 1 тонну)
Доска (за 1 кубометр)
Арматура (за 1 тонну)

Онлайн калькулятор для расчета приблизительной стоимости и количества материалов для заливки монолитного ленточного фундамента для строительства здания

Особенности расчета ленточного фундамента

1. Состав раствора и стоимость материалов, даны для справки.
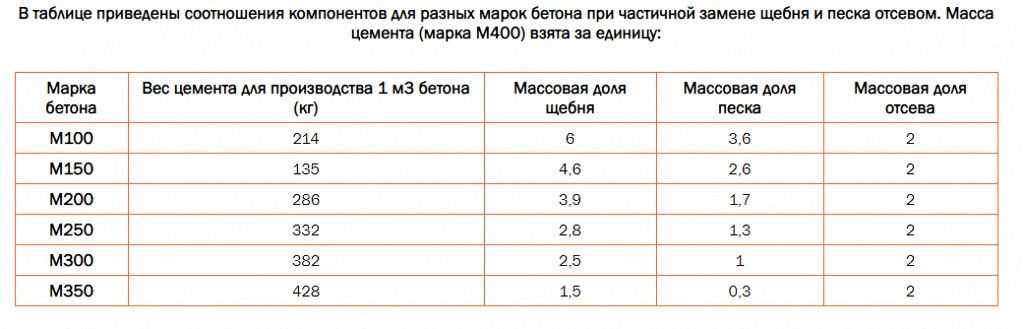
2. Стоимость песка и щебня указывается  за 1 тонну. Поставщики же объявляют цену за кубический метр песка, щебня или гравия. Удельный вес песка зависит от его происхождения. Например, речной песок тяжелее карьерного. 1 кубический метр песка весит 1200-1700 кг, в среднем — 1500 кг.
3. С гравием и щебнем сложнее. По различным источникам вес 1 кубического метра от 1200 до 2500 кг в зависимости от размеров. Тяжелее — более мелкий.

Для того, чтобы избежать чрезмерного давления веса строения на фундамент, ширина его стенок не должна быть уже ширины стен возводимого здания.

Как правило в ленточном фундаменте используют в качестве поперечной арматуры — гладкую арматуру, в качестве продольной арматуры в стальном каркасе фундамента должна быть ребристая арматура

Синонимы: основание, основа, базис, база, опора, fundamentum

людей нашли эту статью полезной. А Вы?

Рассчитать кубатуру фундамента калькулятор

Содержание

1. Калькулятор расчета фундамента.
2. Расчет ленточного фундамента — определяем количество бетона.
3. Как самому рассчитать бетон для фундамента.
4. Калькулятор расчета количества раствора для ленточного фундамента.
5. Калькулятор расчета количества раствора для ленточного фундамента.
6. Пояснения по проведению расчетов.

Калькулятор расчета фундамента.

Фундамент представляет собой основу любого сооружения. Поэтому очень важен выбор правильного и подходящего фундамента, а также грамотный расчет бетона на фундамент, который позволит составить примерную смету строительства.

Рассчитать кубатуру фундамента онлайн калькулятор.

Следует отметить, что смету составлять требуется обязательно, чтобы не пришлось останавливать работы и терять время на приобретение недостающих материалов или же по причине исчерпания бюджета.

Для того чтобы понять сколько средство потребуется затратить на основу сооружения можно использовать специальный калькулятор бетона для фундамента.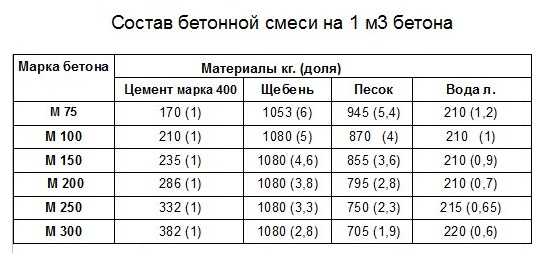

Ленточный фундамент, который может быть монолитным или сборным, представляет собой замкнутую полосу из железобетона, которая разделяет нагрузку сооружения на почву и проходит под несущими стенами конструкции. Такой фундамент предотвращает оседание здания, изменение его формы или деформацию стен. Ленточная основа является самым часто используемым видом фундамента при строительстве частных домов, подвалов и цокольных этажей.

Данный фундамент еще может быть мелкозагубленным или же глубокозагубленным, что зависит от характеристик почвы и предполагаемой нагрузки на него. При возведении любого фундамента важен правильный расчет, что позволит избежать досадных ошибок и лишней траты средств. Калькулятор кубов поможет определить объем требуемого для строительства бетона и заранее запастись всеми составляющими в нужном количестве. Расчет фундамента калькулятор пригодится для определения веса бетонной смеси и нагрузки на почву. Также можно просчитать и расход цементного раствора.

Обычно расчет бетона калькулятор производится по таким характеристикам, как длина, высота и ширина спроектированного фундамента. Для более точных подсчетов можно использовать и дополнительные параметры, например, указать марку используемого бетона и состав смеси. Специализированный калькулятор бетона на фундамент также позволит затем провести анализ, какое количество арматуры может понадобиться или же рассчитать опалубку.

Следует также учитывать, что при приготовлении смеси для строительства
самостоятельно, расчет бетона ведется в зависимости от фракции песка и щебня, их плотность и используемых пропорций.

Калькулятор для ленточного фундамента состоит не только из таких характеристик, как ширина ленты, высота ленты и длина ленты, но и зависит от марки выбранного бетона и толщины ленты.

Расчет ленточного фундамента — определяем количество бетона.

Любая стройка начинается с заложения основания, воспринимающего нагрузку, которую оказывает на него дом или забор. Самым популярным является ленточный фундамент, в состав которого входит бетон и армирующие элементы. Железобетонную ленту закладывают под тяжелые сооружения с массивными перекрытиями. Точный предварительный расчет количества смеси позволяет залить фундамент за один прием, избежать необходимости докупать бетон и тратить деньги на его доставку.

Как рассчитать кубатуру фундамента.

Факторы, влияющие на расчет бетона на ленточный тип фундамента.

Количество бетонной смеси напрямую зависит от линейных размеров основания сооружения. Суммарная длина ленты определяется по проекту: бетон обязательно заливают под наружные стены и несущие простенки. Высота вертикальных граней ленты подбирается с учетом рельефа участка, уровня залегания подпочвенных вод, плотности и пучинистых свойств грунта, а также уровня его промерзания.

Сечение ленты, а затем и ее ширину рассчитывают исходя из характеристик грунта и общей нагрузки на фундамент. Последний параметр определяют как сумму веса сооружения с отделкой, массы жильцов дома, снеговой нагрузки. Расчет площади подошвы выполняют путем деления суммарной нагрузки на табличное значение сопротивления грунта. В формулу включают коэффициент условий работы фундамента – он зависит от сочетания типа грунта и жесткости конструкции.

Полученную опорную площадь умножают на коэффициент надежности. В среднем он составляет 1,2 и соответствует 20%-ному запасу, обеспечивающему снижение давления на основание. Разделив площадь горизонтального сечения ленты на ее высоту, получают искомую величину – ширину ленточного фундамента.

Как самому рассчитать бетон для фундамента.

Определить кубатуру смеси можно самостоятельно, применяя простейшие формулы. Для этого нужно знать ширину ленточного фундамента, его высоту и общую длину. Длина ленты определяется как сумма периметра и несущих простенков. Высота складывается из надземной части и глубины заложения, ширину берут из предварительного расчета несущей способности фундамента.

Условно примем ширину равной 0,3 м, высоту – 1,6 м, длину – 40 м. Бетон рассчитывают как объем параллелепипеда:

V = 0,3 х 1,6 х 40 = 19,2 м3.

Чтобы упростить расчет количества бетона и избежать при этом ошибок, можно использовать программу-калькулятор. Для этого готовят стандартные исходные данные:

• схему ленточного основания;
• длину и ширину дома;
• ширину и высоту ленты.

В программе указано, в каких единицах следует выражать линейные параметры. Обычно калькулятор позволяет рассчитать не только бетон: параллельно выполняется расчет профиля, длины и общего веса арматуры, размеров опалубки, объема теплоизоляционных материалов

Рассчитать кубатуру фундамента.

В качестве примера предлагается определить количество расходных материалов, необходимых для того чтобы заложить основание под дачный однокомнатный домик. В калькулятор вводят параметры из таблицы 1.

Калькулятор расчета количества раствора для ленточного фундамента.

После полного проведения всех подготовительных работ – выкапывания траншей, трамбовки песчано-гравийной подушки, монтажа опалубки и армирующего пояса, переходят к заливке ленты фундамента бетонным раствором. Его можно заказать в готовом виде в соответствующих фирмах, или, при наличии бетономешалки, изготовить на месте самостоятельно.

Рассчитать кубатуру бетона на фундамент калькулятор.

Калькулятор расчета количества раствора для ленточного фундамента.

Но при любом варианте требуется заранее определиться или с объёмом заказа раствора, или с количеством материала для его изготовления. А в этом может оказать помощь размещенный ниже калькулятор расчета количества раствора для ленточного фундамента.

В текстовом блоке ниже калькулятора будут приведены необходимые пояснения.

Калькулятор расчета количества раствора для ленточного фундамента.

Пояснения по проведению расчетов.

Расчет проводится исходя из линейных параметров ленточного фундамента. В программу сразу заложена 10% поправка на создание необходимого запаса.

Для ленточного фундамента в частном строительстве оптимальным станет бетон марки М300 – это обеспечит гарантированную прочность создаваемой конструкции.

Если раствор заказывается в строительной организации, то особых хлопот нет – технологи на производстве знают необходимые пропорции и подготовят бетон нужного качества в требуемых объемах.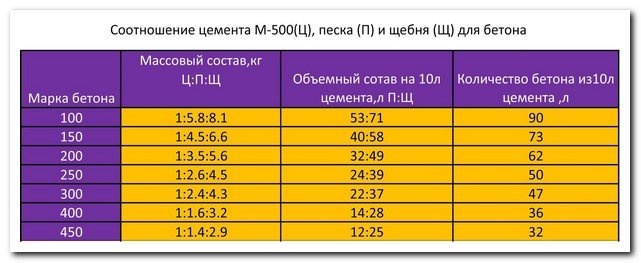

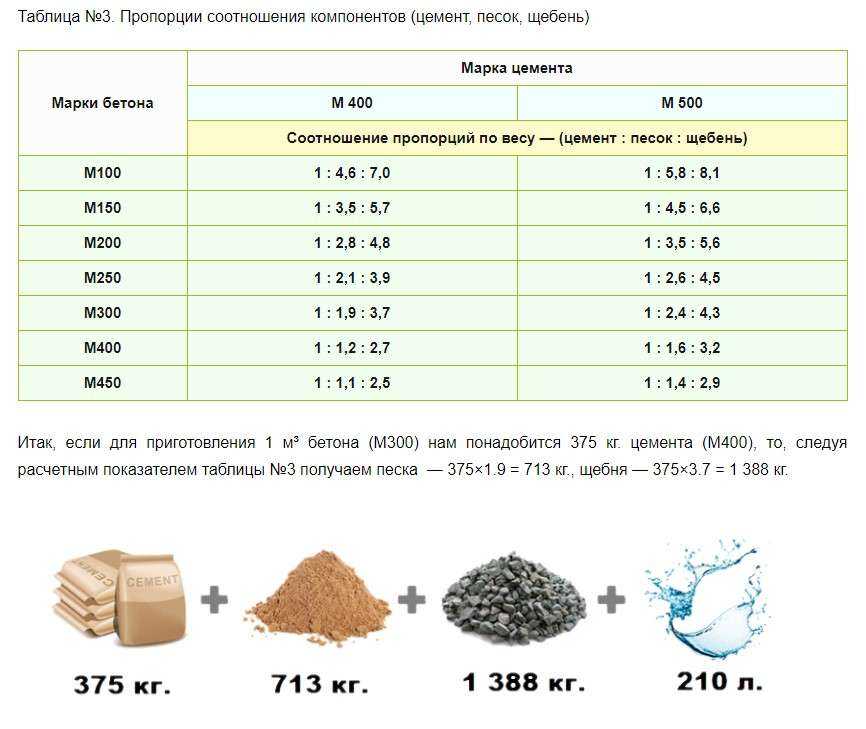
При самостоятельном изготовления бетона количество ингредиентов для замеса придётся отслеживать самому. Для приготовления раствора М300 применяются следующие пропорции:

— портландцемент М400 — 1;

— песок сухой строительный – 1,7;

— гравий (щебень) – 3,2.

Б. По весовому эквиваленту:

— портландцемент М400 — 1;

— песок сухой строительный – 1,9;

— гравий (щебень) – 3,7.

Кроме того, нормативами установлено, что для приготовления 1 кубометра бетона М300 должно расходоваться 0,244 куба цемента М400.

Все эти зависимости внесены в программу калькулятора. В результате будет показано необходимое количество (в весовом и объёмном выражении) всех этих трех компонентов.

Как самостоятельно залить ленточный фундамент?

Помимо проведения необходимых расчетов, требуется знать еще немало технологических нюансов по всем этапам предстоящей работы.

Рассчитать кубатуру фундамента калькулятор.

Калькулятор расчета количества кирпича для кладки цоколя.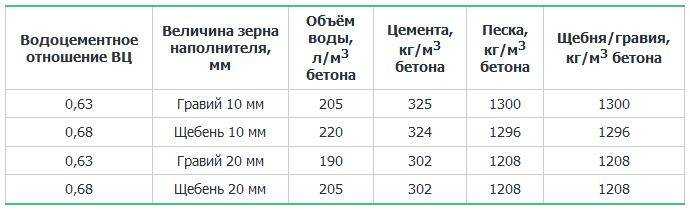

Рассчитать кубатуру фундамента калькулятор.

Калькулятор расчета количества бетона для установки металлических столбов для забора.

Рассчитать кубатуру фундамента калькулятор.

Состав бетона для фундамента пропорции — удобные онлайн-калькуляторы.

Как рассчитать кубатуру фундамента ленточного калькулятор.

Калькулятор количества проволоки для армирования ленточного фундамента.

Рассчитать кубатуру фундамента калькулятор.

Калькулятор расчета несущей способности винтовых свай.

Рассчитать кубатуру фундамента калькулятор.

Калькулятор нагрузки на свайный или столбчатый фундамент.

Рассчитать кубатуру фундамента калькулятор.

Калькулятор количества арматуры для плитного фундамента.

Как рассчитать кубатуру бетона на фундамент.

Калькулятор расчета количества основной арматуры для плитного фундамента.

Рассчитать кубатуру бетона на фундамент калькулятор онлайн.

Калькулятор расчёта минимальной толщины прутьев для основного армирования плитного фундамента.

 

Рекомендация: Это всего лишь обзорная статья, из нее вы только немного узнаете о том как рассчитать кубатуру фундамента калькулятором. Не буду забивать вам голову всякой ерундой. Скажу однозначно, не нужно корчить из себя умников, обратитесь к профессионалам. Зачем ошибаться и терять деньги? Надеюсь, вы разумный человек?!

Расчетные модули > Фундамент > Фундамент общего назначения

 

Нужно больше? Задайте нам вопрос

 

Этот модуль обеспечивает расчет прямоугольного фундамента с приложенной осевой нагрузкой, перекрывающей нагрузкой, моментом и поперечной нагрузкой. Нажмите здесь, чтобы просмотреть видео:

 

Модуль позволяет перемещать положение приложения осевой нагрузки вне центра фундамента и обеспечивает автоматический расчет допустимого увеличения несущей способности грунта на основе размеров фундамента и/или глубины под поверхностью.

 

Модуль проверяет рабочую нагрузку, давление грунта, устойчивость к опрокидыванию, устойчивость к скольжению, изгиб на каждой из четырех поверхностей опоры, сдвиг в одном направлении в точке «d» с каждой из четырех сторон опоры и сдвиг на продавливание по расположенному периметру. ‘d/2’ от граней пьедестала.

Общие

f’c

Прочность бетона на сжатие через 28 дней.

 

fy

Предел текучести арматуры.

 

Ec

Модуль упругости бетона.

 

Плотность бетона

Плотность бетона используется для расчета собственного веса пьедестала и фундамента, если выбран этот параметр.

 

Phi Values ​​

Введите значения снижения производительности, применяемые к Vn и Mn.

 

Двухосный анализ

Выберите «Да» или «Нет», чтобы указать, следует ли выполнять двухосный анализ. Если выполняется двухосный расчет, в решении будут учитываться моменты, действующие одновременно относительно двух ортогональных осей фундамента. Если двухосный анализ НЕ выполняется, решение будет считать, что моменты, приложенные к двум ортогональным осям, действуют не одновременно.

 

Величина длины кромки для M и V (отображается только при выборе двухосного расчета)

При расчете сдвига и момента для фундаментов, где максимальные значения давления ) размера основания от края для использования при расчете моментов и сдвигов из-за переменного давления грунта в этом регионе. Меньшее значение этой переменной приведет к более консервативному расчету, поскольку он будет сосредоточен на более узкой полосе, которая испытывает наибольшее давление грунта.

 

Нажмите, чтобы рассчитать (кнопка отображается только при выборе двухосного анализа)

Из-за итеративного характера расчетов, необходимых для двухосного анализа, было бы нежелательно повторно выполнять весь анализ и проектирование каждый раз, когда изменяется входной параметр. Таким образом, из соображений эффективности программа автоматически переходит в режим ручного пересчета при выборе двухосного анализа. Щелкайте по этой кнопке в любое время, когда вы хотите пересчитать с текущими входными параметрами.

 

Учитывать вес фундамента при определении несущей способности грунта

Выберите этот параметр, чтобы модуль рассчитывал собственный вес фундамента и применял его как нисходящую нагрузку при определении несущей нагрузки грунта. Собственный вес будет умножен на коэффициент статической нагрузки в каждой из комбинаций нагрузок от давления на грунт.

 

Примечание. Обычно следует выбирать этот параметр. Отключение этой опции может привести к неправильным расчетам несущей способности грунта в фундаментах с моментом. Если цель состоит в том, чтобы попытаться сравнить опорное давление грунта с чистым допустимым давлением, то было бы целесообразно использовать параметр на вкладке «Допуски грунта» «Увеличить опорную нагрузку на вес основания».

 

Учитывать вес основания при определении скольжения, опрокидывания и подъема

Выберите этот параметр, чтобы модуль рассчитывал собственный вес основания и применял его в качестве нисходящей нагрузки при определении коэффициентов безопасности скольжения, опрокидывания и подъема. Собственный вес будет умножен на коэффициент статической нагрузки в каждой из комбинаций нагрузки на устойчивость.

 

Игнорировать проверки на скольжение

 Выберите этот вариант, если скольжение по какой-либо конкретной причине не рассматривается при проектировании.

 

Минимальное отношение стали – температура/усадка

Введите минимальное отношение температуры/усадки стали, рассчитанное с использованием полной толщины фундамента. Это вызовет предупреждающее сообщение, если секция недостаточно армирована.

 

Примечание. Эта проверка выполняется при условии, что будет предоставлен только один мат из заданного арматурного стержня. Если конструкция имеет чистое поднятие, так что верхний мат является гарантией, или если верхний мат будет предоставлен в любом случае, имейте в виду, что программа по-прежнему будет учитывать вклад только одного мата в соответствие требованиям к температуре и усадке. В этом случае может оказаться более удобным установить соотношение T&S равным половине общего количества, зная, что двух матов будет достаточно для обеспечения полного требуемого количества.

 

Минимальный коэффициент безопасности при опрокидывании

Введите минимально допустимое отношение момента сопротивления к опрокидывающему моменту.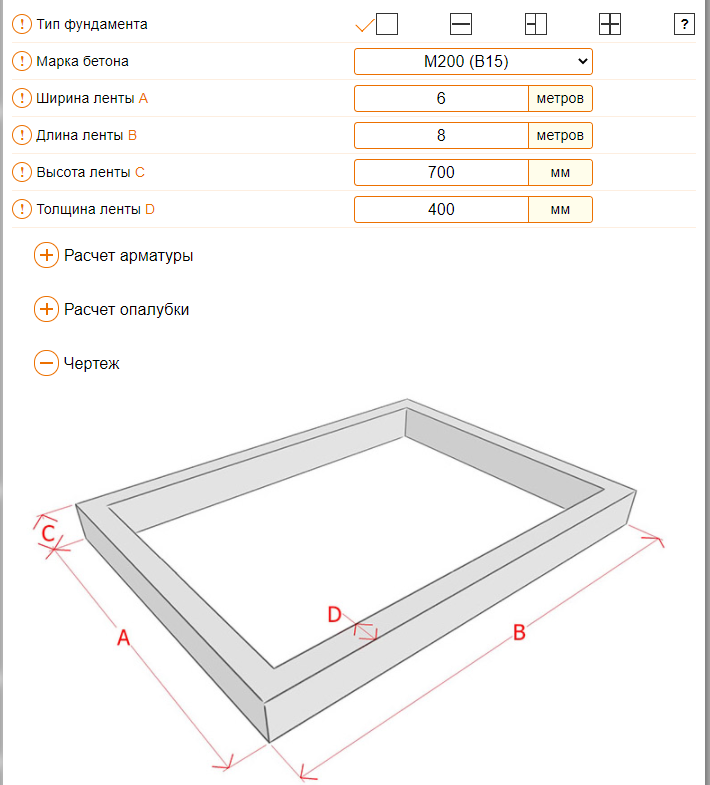 Если фактическое соотношение меньше указанного минимального соотношения, появится сообщение о том, что устойчивость к опрокидыванию неудовлетворительна.

 

Минимальный коэффициент запаса прочности при скольжении

Введите минимально допустимое отношение силы сопротивления к силе скольжения. Если фактическое отношение меньше заданного минимального отношения, появится сообщение о том, что стабильность скольжения неудовлетворительна.

 

Учитывать ACI 10.5.1 и 10.5.3 в качестве минимального усиления

Установите этот флажок, если вы хотите, чтобы модуль учитывал разделы 10.5.1 и 10.5.3 ACI 318 при определении минимального усиления.

 

 

 

Допустимые значения грунта

Допустимое давление грунта

Введите допустимое давление грунта, которому может противостоять грунт. Это сопротивление рабочей нагрузке, которое будет сравниваться с расчетным давлением грунта при рабочей нагрузке (нагрузки не учитываются, как при расчете прочности).

 

Увеличить опору на вес основания

Нажмите [Да], чтобы модуль рассчитал вес одного квадратного фута (вид сверху) веса основания и добавил его к допустимому значению несущей способности грунта. Это приводит к тому, что грунт не подвергается штрафу за собственный вес основания, и полезен в ситуациях, когда в инженерно-геологическом отчете указаны допустимые чистые несущие нагрузки.

 

Пассивное сопротивление грунта скольжению

Введите значение пассивного сопротивления грунта скольжению. Это значение будет использоваться для определения компонента сопротивления скольжению, создаваемого пассивным давлением грунта. Сопротивление скольжению из-за пассивного давления затем добавляется к сопротивлению скольжению из-за трения, чтобы определить общее сопротивление скольжению для каждой комбинации нагрузок.

 

Коэффициент трения между грунтом и бетоном

Введите коэффициент трения между грунтом и основанием для использования в расчетах сопротивления скольжению.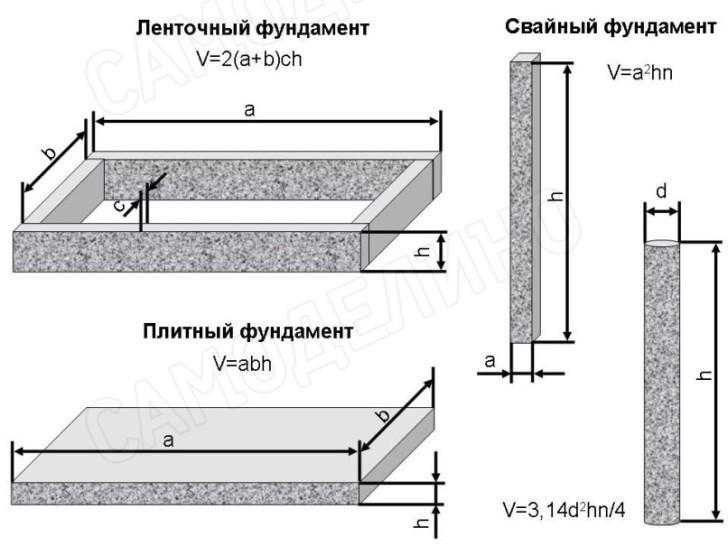

 

Увеличение несущей способности грунта

В этом разделе можно указать некоторые размеры, превышение которых автоматически увеличивает допустимое давление несущей способности грунта.

 

Глубина основания фундамента ниже поверхности почвы: расстояние от нижней части фундамента до верхней части почвы. Это значение используется для определения допустимого увеличения несущей способности грунта и пассивного сопротивления грунта скольжению, но не используется ни в каких других расчетах в этом модуле.

 

Увеличения на основе глубины фундамента: Предоставляет метод автоматического увеличения базового допустимого несущего давления грунта на основе глубины фундамента ниже некоторой опорной глубины. Собирает следующие параметры:  

 

Допустимое увеличение давления на фут: указывает величину, на которую базовое допустимое опорное давление грунта может быть увеличено на каждый фут глубины ниже некоторой контрольной глубины.

 

Если основание фундамента ниже: Указывает требуемую глубину, чтобы начать постепенное увеличение допустимого опорного давления грунта на основе глубины фундамента.

 

Пример: Предположим следующее: Базовое допустимое давление грунта на опору = 3 кгс. Основание фундамента находится на глубине 6 футов-0 дюймов ниже поверхности почвы. В геотехническом отчете указано, что допускается увеличение опорного давления на 0,15 тыс. футов на каждый фут глубины, когда основание находится глубже, чем на 4 фута ниже поверхности почвы. Поскольку вы указали, что если фундамент находится на 6 футов ниже поверхности почвы, модуль автоматически рассчитает скорректированное допустимое давление на грунт как 3 тыс.фут + (6 – 4 фута) * 0,15 тыс.фунт = 3,30 тыс.фунт.0003

 

Увеличения на основе размера фундамента: Предоставляет метод автоматического увеличения базового допустимого несущего давления грунта на основе размеров фундамента, превышающих какой-либо контрольный размер. Собирает следующие параметры:

 

Допустимое увеличение давления на фут: указывает величину, на которую базовое допустимое опорное давление грунта может быть увеличено на каждый фут длины или ширины, превышающей некоторый эталонный размер.

 

Когда максимальная длина или ширина больше: Указывает требуемый размер, чтобы начать поэтапное увеличение допустимого несущего давления грунта на основе размера фундамента.

 

Пример: Предположим следующее: Базовое допустимое давление грунта на опору = 3 кгс. Фундамент измеряет 12′-0″ x 6′-0″. В геотехническом отчете указывается, что допустимо увеличение опорного давления грунта на 0,15 тыс. футов на каждый фут, если наибольший размер фундамента в плане превышает 4 фута. Модуль автоматически рассчитает скорректированное допустимое давление на грунт как 3 тыс. футов + (12 футов — 4 фута) * 0,15 тыс. футов = 4,2 тыс. футов.

 

Примечание. Увеличение в зависимости от глубины фундамента и размеров в плане является кумулятивным.

 

 

 

Размеры основания

На этой вкладке вы вводите размеры основания и пьедестала.

 

Ширина, длина и толщина: определяет габаритные размеры основания.

 

Расположение нагрузки: определяет смещение от центра основания, в котором действует осевая нагрузка. Если двухосный анализ НЕ используется, то можно использовать только одно направление.

 

Размеры пьедестала: Если бетонный пьедестал опирается на фундамент, его размеры можно указать здесь. Размеры px и pz используются для определения мест на всех четырех сторонах, где рассчитывается односторонний сдвиг, двусторонний сдвиг и изгибающий момент. Если вы введете ненулевую высоту, вы можете выбрать, чтобы вес этой призмы был рассчитан и добавлен как статическая нагрузка. Любые приложенные нагрузки от вскрыши будут исключены из области, определяемой как размер основания вдоль осей xx и yy, независимо от заданной высоты призмы.

 

Примечание. Если пьедестал не определен, то центр фундамента будет рассматриваться как поверхность пьедестала при определении критических мест для проверки на сдвиг и изгиб.

 

 

 

Учитывать вес пьедестала при определении: этот параметр позволяет пользователю указать, следует ли учитывать собственный вес пьедестала при определении несущей — при проверках на скольжение, опрокидывание и подъем следует учитывать вес пьедестала.

 

Армирование фундамента

На этой вкладке можно указать армирование в каждом направлении фундамента.

 

 

Приложенные ВЕРТИКАЛЬНЫЕ нагрузки

На этой вкладке можно указать осевую нагрузку, приложенную к расположению пьедестала, и нагрузку от перекрывающих пород, приложенную ко всему размеру фундамента в плане (за исключением области, обозначенной как пьедестал).

 

Введите нагрузки с положительным знаком для направления вниз.

 

Внимание! Этот модуль не допускает поднятия сетки на фундаменте. Если результат факторизованных осевых нагрузок (стационарная, динамическая, ветровая и т. д.) дает отрицательный знак нагрузки, модуль не будет пересчитывать и уведомит вас о том, какая комбинация нагрузок привела к чистому подъему.

 

 

Приложенные изгибающие нагрузки

На этой вкладке можно ввести приложенные моменты.

 

 

Приложенные сдвиговые нагрузки

На этой вкладке можно ввести приложенные поперечные силы. Эти нагрузки приложены в месте расположения пьедестала. Если указана высота пьедестала, сдвиг будет применяться на этой высоте и создаст момент на основании, равный поперечной нагрузке * (толщина основания + высота пьедестала).

 

 

Сочетания нагрузок — обслуживание

Это типичная вкладка сочетаний нагрузок, используемая в библиотеке проектирования конструкций. Вкладка «Комбинации услуг» используется для расчета давления на грунт, которое необходимо сравнить с допустимым давлением на грунт. «Увеличение грунта» — это коэффициент, который можно указать отдельно для каждой комбинации нагрузок и который применяется к допустимому давлению на грунт.

 

 

Сочетания нагрузок — с учетом фактора

Это типичная вкладка сочетаний нагрузок, используемая в Библиотеке проектирования конструкций для расчета прочности. Эти комбинации нагрузок используются для расчета моментов и сдвигов в фундаменте для определения напряжений и требуемой арматуры.

 

Примечание. Модуль «Общее основание» применяет факторизованные нагрузки к основанию и определяет другой эксцентриситет, чем тот, который был определен с использованием эксплуатационных нагрузок для проверки опорного давления грунта.

 

 

Вкладка «Результаты»

На этой вкладке представлена ​​сводка всех рассчитанных значений. Сообщаются коэффициенты напряжений, применяемые и допустимые значения, а также сочетания нагрузок для этих основных значений.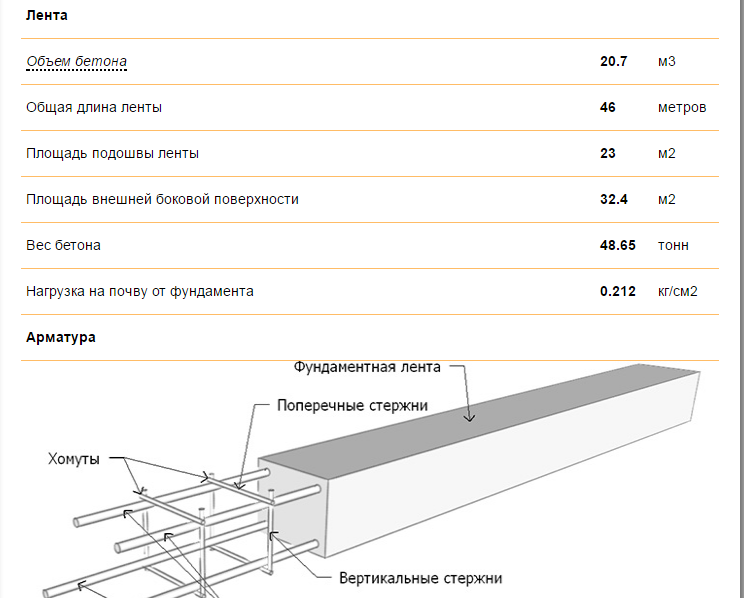

 

 

Вкладка «Давление грунта»

На этой вкладке приведены расчетные значения давления грунта на рабочую нагрузку для моментов и сдвигов, приложенных к указанной оси, для каждой комбинации нагрузок.

 

 

Вкладка «Устойчивость к опрокидыванию»

На этой вкладке представлены расчеты устойчивости фундамента к опрокидыванию и моменту сопротивления относительно каждой оси и для каждой комбинации нагрузок. Обратите внимание, что используемые здесь сочетания нагрузок генерируются внутренними силами, а НЕ из сочетаний эксплуатационных нагрузок, которые вы ввели для оценки несущего давления грунта.

 

Обратите внимание, что программа настроена на индивидуальный поиск сил опрокидывания и сопротивления. Например, возьмем ситуацию, когда основание подвергается равным и противоположным сдвигам на заданной высоте. Здравый смысл подсказывает, что эти силы компенсируют друг друга, и основание не испытывает от них чистого приложенного опрокидывающего момента.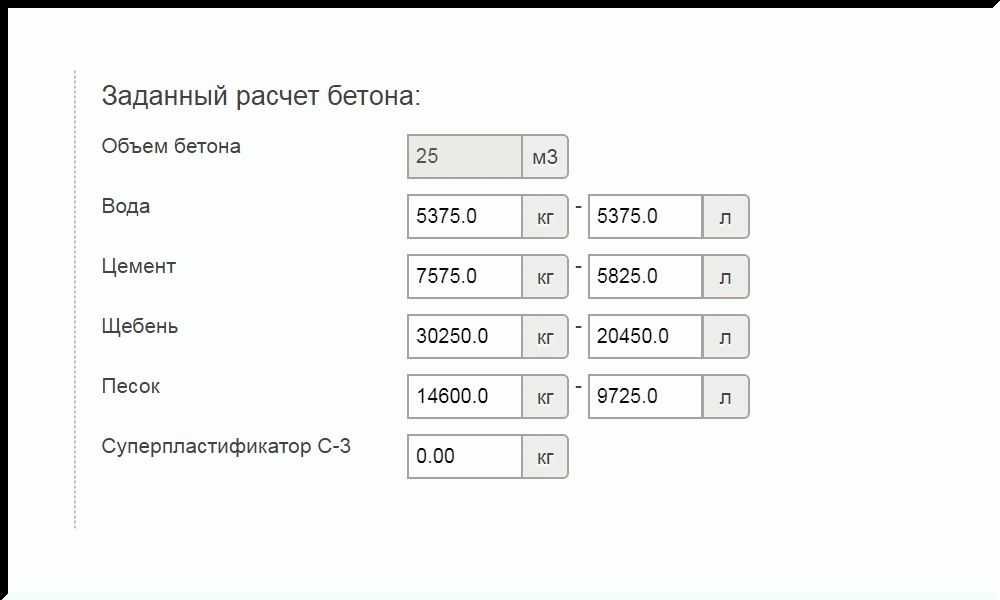 Но программа рассматривает одну из двух равных и противоположных сил как опрокидывающую силу, а другую — как противодействующую. Таким образом, для этих двух сил сообщается чистый опрокидывающий момент, но момент сопротивления ТАКЖЕ учитывает влияние противодействующей нагрузки, поэтому учет, используемый для определения коэффициента опрокидывания, является правильным.

 

 

Вкладка «Устойчивость к скольжению»

На этой вкладке представлены расчеты приложенной и сопротивляющейся устойчивости фундамента к скольжению в каждом направлении оси и для каждого сочетания нагрузок. Обратите внимание, что используемые здесь сочетания нагрузок генерируются внутренними силами, а НЕ из сочетаний эксплуатационных нагрузок, которые вы ввели для оценки несущего давления грунта.

 

 

Вкладка для изгиба основания

На этой вкладке представлены сводные данные расчетного момента нагрузки с учетом факторов на всех четырех краях периметра опоры для каждого сочетания нагрузок.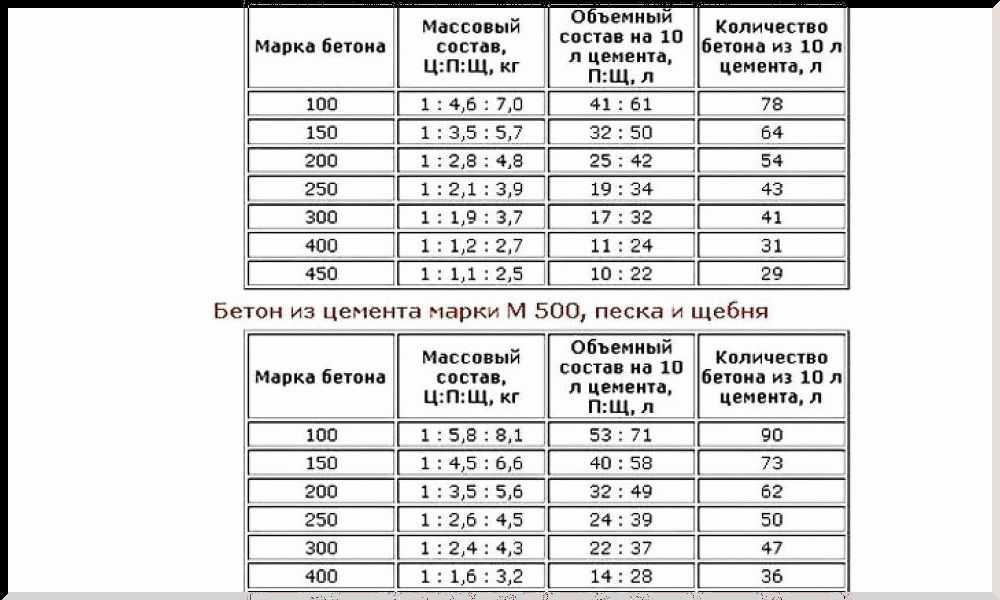 Он указывает, вызывает ли указанное сочетание нагрузок растяжение верхней или нижней поверхности фундамента.

 

Примечание. В случаях, когда напряжение возникает в верхней части фундамента, проверка на изгиб будет основываться на предположении, что на верхней поверхности фундамента предусмотрен определенный арматурный мат. Пользователь должен просмотреть результаты и определить, действительно ли для каких-либо комбинаций нагрузок требуется армирующий верхний мат или можно ли усилить основание только нижним матом.

 

 

Вкладка «Сдвиг основания»

На этой вкладке представлены сводные данные расчетного сдвига с учетом факторов нагрузки на всех четырех краях периметра опоры для каждой комбинации нагрузок. Также рассчитывается двухсторонний или продавливающий сдвиг.

 

 

Вкладка «Эскиз»

 

 

Исследование метода расчета нелинейной осадки фундамента на этой странице

Загрузка на месте0003

РезюмеВведениеВыводыДоступность данныхКонфликты интересовБлагодарностиСсылкиАвторское правоСтатьи по теме

В данной статье предлагается метод нелинейного модуля деформации для расчета осадки фундамента. В предлагаемом методе модуль нелинейной деформации при различных уровнях напряжения получается из кривой нагрузки-осадки испытания на нагрузку на месте, которые затем применяются к методу послойного суммирования для расчета осадки фундамента. На этой основе и со ссылкой на модель Дункана-Чанга далее предлагается конститутивная модель переменного модуля, подходящая для численного расчета осадки фундамента. Требуемые параметры этой модели такие же, как и у метода нелинейного модуля деформации, и их можно определить с помощью испытания на нагрузку на месте. Правомерность предложенных методов расчета осадки фундамента подтверждается испытаниями на нагрузку на месте при различных размерах плит. Результаты показывают, что как метод нелинейного модуля деформации, так и определяющая модель переменного модуля достаточно хорошо согласуются с результатами испытаний, а полученные результаты могут лучше отражать нелинейность осадки фундамента.

1. Введение

Расчет осадки фундамента является основным и важным содержанием в области механики грунтов. Обычно используемые методы расчета осадки в основном ориентированы на отбор проб грунта и лабораторные испытания на сжатие, а выведенная кривая сжатия используется для расчета осадки. Несмотря на то, что этот метод относительно прост и практичен, существуют два серьезных теоретических недостатка, которыми нельзя пренебречь: (i) во время отбора проб почвы может произойти нарушение целостности образца; (ii) условия напряжения и деформации лабораторного испытания на сжатие сильно отличаются от полевых условий, что затрудняет оценку погрешности расчета. Поскольку лабораторные испытания не могут точно отразить фактические характеристики деформации грунта на месте, трудно вывести точные результаты осадки фундамента даже с использованием современных передовых методов численного расчета. Таким образом, лучшим способом является улучшение получения расчетных параметров, а именно расчет осадки фундамента на основе параметров, полученных в результате испытаний на месте. Это может повысить точность расчета осадки фундамента, что может более точно отражать деформационные характеристики фундамента. В настоящее время известны некоторые методы расчета осадки фундамента на основе результатов натурных испытаний [1–5]. Например, Ли [4] предложил метод расчета осадки фундамента, основанный на тесте на проникновение конуса с учетом различных условий пласта. Чжан и др. В [5] предложен нелинейный метод расчета осадки, основанный на расчетных параметрах, полученных в результате прессиометрических испытаний. Однако большинство из этих методов в основном обеспечены опытом.

Испытание под нагрузкой на месте считается одним из самых надежных методов определения предельной несущей способности фундамента. Одновременная кривая нагрузки-осадки может реалистично отражать характеристики деформации фундамента в процессе нагружения. Кроме того, можно определить модуль деформации натурного грунта, что может быть эффективно применено при расчете осадки фундаментов [6–10]. Кроме того, фактический процесс осадки фундамента является нелинейным, и использование одного постоянного модуля деформации не может точно отражать характеристики нелинейной деформации фундамента, на которые воздействуют нагрузки. Таким образом, в этом исследовании модуль нелинейной деформации при различных уровнях напряжения получается из кривой нагрузки-осадки испытания на нагрузку на месте, которые затем применяются к методу послойного суммирования и численной определяющей модели для расчета осадки фундаментов. На основе этих обработок устанавливается и предлагается метод расчета нелинейной осадки фундамента, основанный на нагрузочных испытаниях на месте. Правомерность предлагаемого метода расчета подтверждается испытаниями на нагрузку на месте при различных размерах пластин.

2. Метод нелинейного модуля деформации для расчета осадки фундамента

2.1. Метод нелинейного модуля деформации

Предполагая, что слой грунта толщиной, расположенной на глубине, подвергается малой добавочной нагрузке , деформацию этого слоя грунта можно приблизительно представить как линейный процесс и представить следующим образом. где – модуль деформации слоя грунта на глубине при внешнем нагружении; является коэффициентом распределения напряжения и определяет приращение напряжения, создаваемое дополнительной нагрузкой.

Тогда, в соответствии с методом послойного суммирования, общая осадка всех слоев при возрастающей нагрузке может быть суммирована как где относится к общему количеству слоев почвы.

Ключевым аспектом вышеуказанного метода расчета является обоснованное определение модуля деформации. Из предыдущего анализа видно, что кривая нагрузки-осадки, полученная при испытании на нагрузку на месте, может более точно отражать деформационные характеристики фундаментов в процессе нагружения, и соответственно можно определить модуль деформации грунта фундамента. Предыдущие исследования [11–14] показывают, что кривая нагрузки-осадки (-), полученная в результате испытания на нагрузку на месте, обычно выражается гиперболической функцией. где и – неизвестные коэффициенты, которые необходимо определить. Согласно характеристикам гиперболической функции и теории упругой механики [11] где длина стороны или диаметр пластины для испытания на нагрузку на месте; – коэффициент Пуассона почвы; – коэффициент, отражающий форму и жесткость пластины, для жестких квадратных и круглых пластин, значения которых соответственно равны 0,88 и 0,79; – начальный модуль деформации грунта; в то время как предельная нагрузка.

Кроме того, осадку фундамента, вызванную испытанием на нагрузку на месте, можно приблизительно рассчитать с помощью решения Буссинеска механики упругости: где – модуль деформации грунта в нижней части плиты, соответствующий приложенной нагрузке.

Преобразование из уравнения (5) можно найти, что

Из уравнения (3) касательная производная кривой -, полученная в результате испытания на нагрузку на месте, в любой точке может быть выражена как

Предполагая, что и подставляя уравнения (7) и (4) в уравнение (6), модуль деформации грунта в нижней части нагрузочной плиты равен

В приведенном выше уравнении – это отношение нагрузки к предельной нагрузке грунта основания в нижней части нагрузочной плиты, которое отражает влияние уровня напряжения на модуль деформации грунта. Для грунтов разной глубины дополнительная нагрузка после диффузии уменьшается, а соответствующая предельная нагрузка увеличивается с увеличением глубины, что приводит к увеличению модуля деформации по уравнению (8).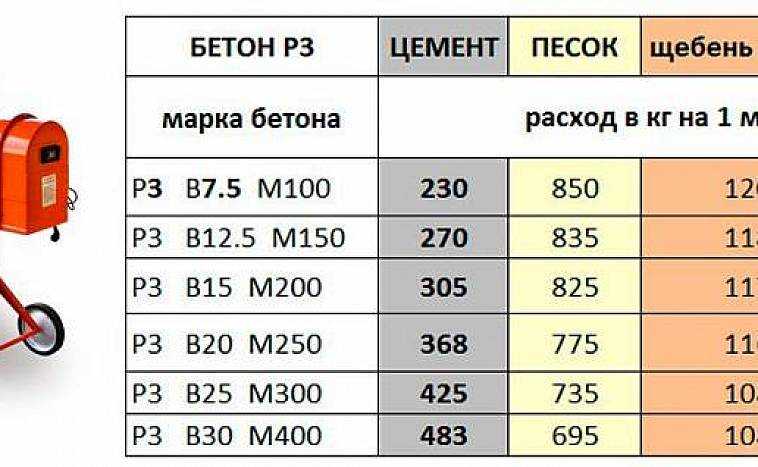 Это соответствует характеристикам нелинейной деформации фундамента. Затем, применяя модуль деформации грунта на разных глубинах к методу послойного суммирования, а именно, подставляя уравнение (8) в уравнения (1) и (2), производят расчет осадки основания, который называется нелинейным модулем деформации метод в этой статье.

2.2. Определение параметров на основе испытаний на нагрузку на месте

Из приведенного выше раздела можно сделать вывод из уравнения (8), что метод нелинейного модуля деформации должен определять предельную нагрузку грунта и начальный модуль деформации , при этом можно рассчитать в соответствии с сцепление и угол внутреннего трения грунта и размер плиты. Следовательно, для метода нелинейного модуля деформации необходимо определить три параметра грунта (т.е. , , и ). Чтобы преодолеть недостатки определения параметров в лабораторных испытаниях, в этом исследовании эти три параметра получены на основе испытаний на нагрузку на месте.

Обратите внимание, что кривую оседания нагрузки (- s ) можно легко получить из испытаний на нагрузку на месте.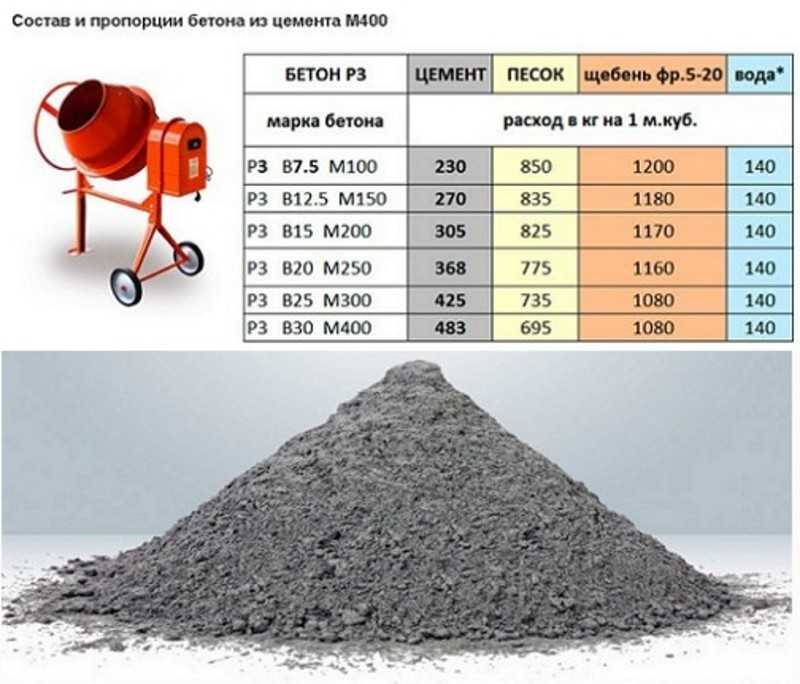 Используя гиперболическую функцию в качестве входных данных для подбора кривой — s , можно легко вывести коэффициенты и , которые можно непосредственно применить для обратного расчета параметров , и для метода нелинейного модуля деформации.

Значения и могут быть рассчитаны обратным образом из уравнения предельной несущей способности Vesic. где , , и – коэффициенты несущей способности и могут быть получены по значению; , , и – коэффициенты формы пластины при испытании на нагрузку на месте; дополнительная нагрузка, приложенная к обеим сторонам пластины; — удельный вес грунта, который равен эффективному весу ниже уровня грунтовых вод.

Следует отметить, что в уравнении (9) есть только два неизвестных параметра, а именно, и . Для песка и может быть обратно рассчитана из предельной несущей способности () грунтов основания, полученной в результате испытаний на нагрузку на месте. Таким образом, для глины один из этих двух параметров принимается эмпирически, а значение другого параметра может быть рассчитано обратно пропорционально предельной несущей способности ().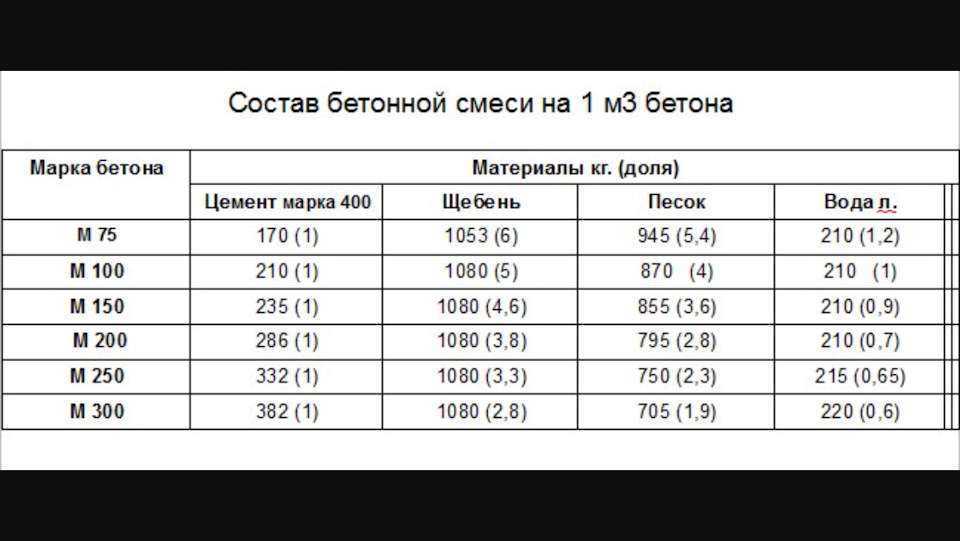

Начальный модуль деформации грунта определяется решением Буссинеска механики упругости. Когда коэффициент гиперболической функции подобран в соответствии с — кривая нагрузочных испытаний на месте, выражение для значения

3. Конститутивная модель переменного модуля для расчета осадки фундамента

В настоящее время определение параметров конститутивной модели грунтов в основном сосредоточено на лабораторных испытаниях. Однако для сильных структурных грунтов на результаты лабораторных испытаний может сильно повлиять снятие напряжения и возмущение, вызванное отбором проб, что приводит к совершенно другим результатам по сравнению с фактическими. Таким образом, трудно обеспечить точность расчетных результатов по параметрам лабораторных испытаний. Между тем, поскольку конститутивные свойства почв весьма сложны, установить конститутивную модель, объединяющую все характеристики почв, практически невозможно. В таком конкретном случае создание практической конститутивной модели, отражающей основные характеристики и параметры, которые легко измерить, более эффективно и имеет большое значение.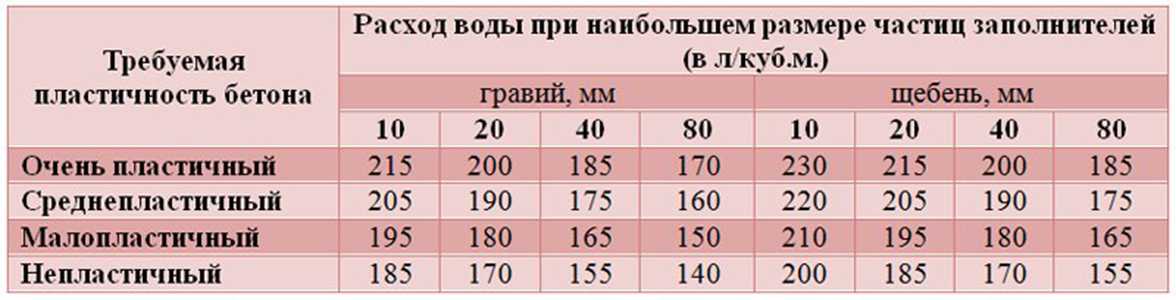

Следует отметить, что основной особенностью задачи осадки фундамента является то, что деформации грунтов носят нелинейный характер [15–17]. Модель Дункана-Чанга, основанная на обобщенном законе Гука, широко используется в практической инженерной практике, поскольку позволяет легко определить необходимые параметры и в дальнейшем может отражать наиболее заметные характеристики деформации (т. е. нелинейность) грунтов. Однако, поскольку эти требуемые параметры обычно определяются с помощью обычного испытания на трехосное сжатие в лаборатории, оно также имеет определенные ограничения, особенно для некоторых прочных структурных грунтов. Чтобы объединить преимущества и компенсировать ограничения в определении параметров модели Дункана-Чанга, предлагается упрощенная модель Дункана-Чанга, называемая в этой статье конститутивной моделью с переменным модулем, на основе метода нелинейного модуля деформации и метода Дункана. -Модель Чан. Следовательно, конститутивная модель где , , , , , и – компоненты приращения напряжения; , , , , , – компоненты приращения деформации; представляет собой упругую матрицу и определяется выражением где и определяют модуль деформации и коэффициент Пуассона грунта соответственно. В конститутивной модели переменного модуля упрощенные выражения этих двух параметров следующие:

В приведенных выше двух уравнениях и , соответственно, относятся к начальному модулю деформации и коэффициенту Пуассона грунта. – коэффициент Пуассона грунта в состоянии предельного разрушения и обычно равен 0,49. — предел прочности грунтов по критерию разрушения Мора-Кулона и выражается как

Из приведенного выше анализа можно сделать вывод, что основные параметры конститутивной модели переменного модуля включают сцепление , угол внутреннего трения , начальный модуль деформации и начальный коэффициент Пуассона . Как правило, он приблизительно равен 0,3, а другие три параметра грунта (т. е. , , и ) можно определить с помощью испытаний на нагрузку на месте. Следовательно, определяющая модель переменного модуля, основанная на параметрах испытаний на месте, может быть легко установлена ​​как простая, но практичная определяющая модель для расчетов осадки фундамента.

4.

Испытания и проверки на месте

4.1. Испытания на месте

Чтобы проверить как метод нелинейного модуля деформации, так и определяющую модель переменного модуля для расчета осадки фундамента, был выбран репрезентативный прочный структурный гранитный остаточный грунт в Гуанчжоу (Китай) и проведено несколько серий испытаний на нагрузку на месте с размер квадратных пластин, равный 1 м ² () и 2 м ² (). Полученный — кривые испытаний плиты на нагрузку на месте показаны на рисунке 1. Видно, что испытание 1 # нагружалось на 50 кПа на каждом этапе, а испытания 2 # и 3 # нагружались на 60 кПа на каждом этапе, а — Кривые двух испытаний под нагрузкой на месте 1# и 2# с одинаковым размером плиты (1  м ² ) в основном одинаковы. Кроме того, быстрое увеличение осадки свидетельствует о том, что нагрузка, приложенная к испытанию 2#, почти достигает предельной несущей способности гранитного остаточного грунта.

Для сравнения, лабораторные испытания, включая испытания физических свойств почвы и обычные испытания на трехосное сжатие, также проводились с образцами почвы. Глубина отбора проб составляет 1,0 м и 2,5 м соответственно. Полученные результаты испытаний представлены в таблице 1 и на рисунке 2.

4.2. Проверки

4.2.1. Проверка метода нелинейного модуля деформации

Согласно предыдущему анализу, метод нелинейного модуля деформации требует трех параметров грунта: , , и , и эти три параметра могут быть легко получены из результатов испытаний на нагрузку на месте. В настоящем исследовании параметры , , и гранитного остаточного грунта определяются на основе результатов нагрузочного испытания на месте 2# (как показано на рисунке 1). Затем используется метод нелинейного модуля деформации для расчета — , которые сравниваются с результатами нагрузочных испытаний на месте 1# и 3# и подтверждают рациональность метода нелинейного модуля деформации.

По результатам испытания на нагрузку на месте 2# (как показано на рисунке 1) наблюдалось быстрое увеличение осадки, когда приложенная нагрузка увеличивается с 780 кПа до 840 кПа, что указывает на то, что эта приложенная нагрузка почти достигает предельная несущая способность гранитного остаточного грунта. Принимая среднее значение двухступенчатых нагрузок в качестве предельной несущей способности, таким образом, значение равно 815 кПа, а параметры и могут быть вычислены обратным образом после подстановки значений в уравнение (9).). По эмпирическому значению параметров грунта в Гуанчжоу принято, что угол трения гранитного остаточного грунта () равен 25°; тогда расчетное сцепление грунтов () равно 25 кПа.

После перезаписи уравнения (3) упрощенное выражение формы будет

Используя уравнение (15) для подгонки кривой — испытания на нагрузку на месте 2#, полученное соотношение

На рис. 3 показана согласованная зависимость результатов испытания на нагрузку на месте 2#. Как видно из рисунка 3, эти результаты могут быть очень хорошо выражены в виде гиперболических функций, а подобранный коэффициент гиперболической функции равен 0,0261. Таким образом, начальный модуль деформации гранитного остаточного грунта может быть получен из уравнения (10) и представлен следующим образом.

В таблице 2 представлены расчетные параметры , , и метода нелинейного модуля деформации, полученные по результатам испытания на нагружение на месте 2#. Расчетные результаты кривых — с идентичными условиями нагружения, как и при испытаниях на месте 1# и 3# методом нелинейного модуля деформации, показаны на рисунке 4. Также включены соответствующие результаты испытаний на месте. Видно, что кривые — , рассчитанные методом нелинейного модуля деформации, очень хорошо согласуются с результатами испытаний на месте, что в первую очередь подтверждает рациональность метода нелинейного модуля деформации.

4.2.2. Проверка определяющей модели с переменным модулем

Для определяющей модели с переменным модулем также требуются три параметра , и , и они также могут быть получены по результатам испытаний на нагрузку на месте. Аналогичным образом значения , , и гранитного остаточного грунта определены по результатам нагрузочных испытаний 2# на месте и представлены в табл. 3. В этом разделе рациональность модели переменного модуля проверяется сравнением численных результаты с использованием FLAC ^3D и результаты нагрузочных испытаний на месте 1# и 3#. Расчетная сетка показана на рис. 5, а соответствующие сравнения показаны на рис. 6. Кривые –, рассчитанные с помощью численного анализа на основе конститутивной модели с переменным модулем, хорошо согласуются с результатами полевых испытаний, которые подтверждают рациональность предложенная конститутивная модель переменного модуля.

Известно, что модель Дункана-Чанга может отражать характеристики нелинейной деформации грунтов основания, но требуемые параметры в основном получают из обычных трехосных испытаний. Для сравнения с расчетными результатами конститутивной модели переменного модуля соответствующие численные результаты модели Дункана-Чанга также включены в рисунок 6. Расчетные параметры модели Дункана-Чанга показаны в таблице 4.

Как видно из рисунка 6, численные результаты модели Дункана-Чанга, основанные на обычных параметрах трехосных испытаний, сильно отличаются от результатов испытаний на нагрузку на месте и численных результатов определяющей модели с переменным модулем. Основная причина может заключаться в том, что гранитный остаточный грунт имеет сильные структурные характеристики [18–21], а эффекты снятия напряжения и возмущения, вызванные отбором проб, приводят к большим различиям между параметрами лабораторных испытаний и фактическими. Несмотря на то, что конститутивная модель переменного модуля является упрощенной моделью, основанной на модели Дункана-Чанга, она может отражать нелинейную деформацию грунта основания, а ее параметры получены в результате испытаний на месте. Сравнивая численные результаты с результатами испытаний на нагрузку на месте, конститутивная модель переменного модуля, основанная на параметрах испытаний на месте для расчета нелинейной осадки фундамента, имеет некоторое преимущество перед моделью Дункана-Чанга, основанной на обычных параметрах трехосного испытания.

5. Выводы

В этом исследовании предложены нелинейный метод модуля деформации и определяющая модель переменного модуля для расчета осадки фундамента на основе испытания на нагрузку на месте. Достоверность этих двух расчетных моделей подтверждается сравнением результатов расчетов с результатами испытаний на нагрузку на месте при различных размерах пластин. Основные выводы можно резюмировать следующим образом: (1) Параметры расчета, которые могут отражать ненарушенный характер и нелинейность деформации грунта при фактическом напряженном состоянии, являются ключевыми факторами, которые непосредственно влияют на точность расчета осадки фундамента. Метод нелинейного модуля деформации и определяющая модель переменного модуля, предложенные на основе испытания на нагрузку на месте в этой статье, могут лучше учитывать эти два ключевых фактора. это исследование очень хорошо сравнивается с результатами испытаний на нагрузку на месте при различных размерах пластин, которые также могут лучше отражать нелинейность осадки фундамента (3). Требуемые параметры как метода нелинейного модуля деформации, так и определяющей модели переменного модуля: сцепление угол внутреннего трения и начальный модуль деформации грунтов, которые являются общими параметрами для практического проектирования и могут быть легко определены

Доступность данных

Некоторые или все данные, модели или код, подтверждающие результаты этого исследования, можно получить у соответствующего автора по обоснованному запросу.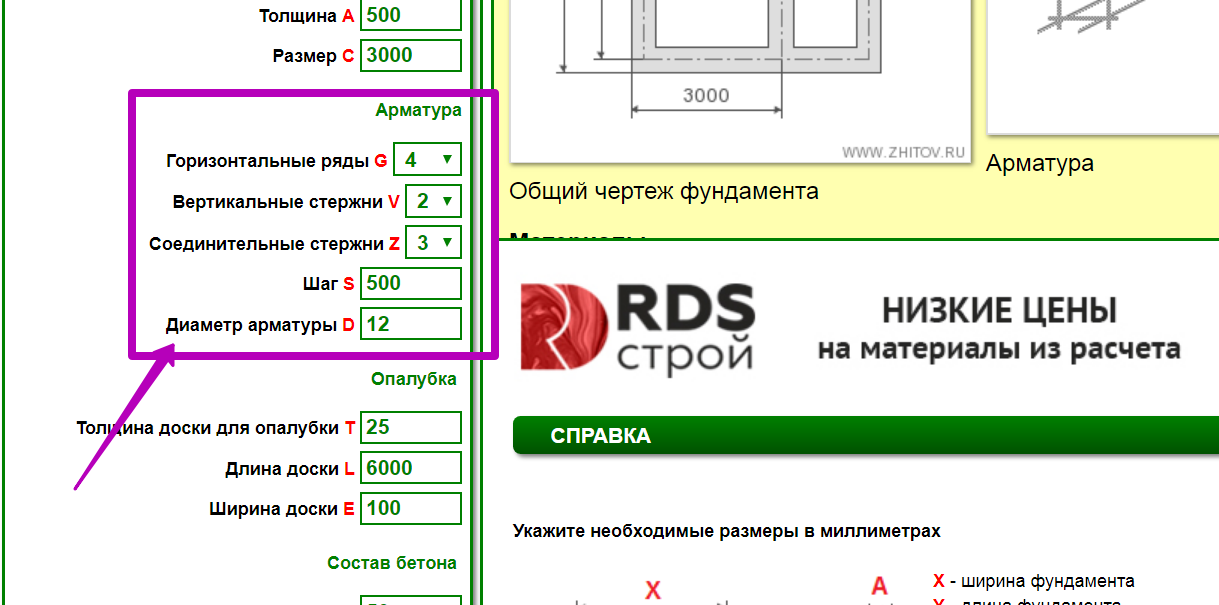

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Благодарности

Это исследование поддерживается Гуандунским фондом фундаментальных и прикладных фундаментальных исследований (№ 2020A1515110215) и Национальным фондом естественных наук Китая (№ 52078143).

Ссылки

1. Г. Чжан, П. К. Робертсон и Р. В. И. Брахман, «Оценка осадки грунта, вызванной разжижением, по CPT для ровного грунта», Canadian Geotechnical Journal , vol. 39, нет. 5, стр. 1168–1180, 2002.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

2. П. Пишга и Р. Дж. Ченари, «Меры надежности для расчета консолидации с помощью данных CPT», International Journal of Civil Engineering , том. 12, нет. 2, pp. 180–185, 2014.

   Просмотр по адресу:

   Google Scholar

3. М. Мир, А. Буафия, К. Рахмани, Н. Ауали, «Анализ характеристик нагрузки при осадке мелкозаглубленных фундаментов» в насыщенных глинах на основе испытаний СРТ и ДПТ», Геомеханика и машиностроение , вып. 13, нет. 1, стр. 119–139, 2017.

   Посмотреть по адресу:

   Google Scholar

4. П. Ли, «Расчет осадки фундамента на основе технологии испытаний на проникновение конуса», China Railway Science , vol. 39, нет. 3, pp. 8–14, 2018.

   Просмотр по адресу:

   Google Scholar

5. Ю. К. Чжан, Х. Ю. Ху, Г. Х. Ян, З. Х. Чжун, К. Лю и С. Ю. Лю, «Метод расчета нелинейной осадки» на основе параметров грунта, полученных в результате прессометрических испытаний», Китайский журнал геотехнической инженерии , том. 42, нет. S1, стр. 38–44, 2020.

   Посмотреть по адресу:

   Google Scholar

6. В. Ю. Цзяо, «Новый параметр в расчете теории осадки грунтового основания и применении модуля хорды», Гидрогеология и инженерная геология , вып. 1, стр. 30–33, 1982 г. (на китайском языке)).

   Посмотреть по адресу:

   Google Scholar

7. Дж. Б. Андерсон, Ф. К. Таунсенд и Л. Рахелисон, «Испытания под нагрузкой и прогнозирование осадки мелкозаглубленного фундамента», Journal of Geotechnical and Geoenvironmental Engineering , vol. 133, нет. 12, стр. 1494–1502, 2007.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

8. Г. Х. Ян, «Новый метод расчета осадок грунтовых оснований», Китайский журнал горной механики и инженерии , том. 27, нет. 4, стр. 679–686, 2008.

   Просмотр по адресу:

   Google Scholar

9. Р. П. Ли, «Анализ нелинейной осадки фундаментов на основе полевых испытаний», Rock and Soil Mechanics , vol. 30, нет. 2, pp. 345–351, 2009.

   Просмотр по адресу:

   Google Scholar

10. Тарауна Б., Нусайрат Дж. и Хакам Й. Испытание под нагрузкой и осадка мелкозаглубленного фундамента на песках пустыни, стр. Геотехническая инженерия , том. 171, нет. 1, стр. 52–63, 2018 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

11. Г. Х. Ян, «Метод гиперболической модели для расчета нелинейной осадки фундамента [J]», Ground Improvement , vol. 8, нет. 1, стр. 50–53, 1997.

    Просмотр по адресу:

    Google Scholar

12. Р. П. Ли, «Нелинейная осадка грунта, рассчитанная с помощью уравнения касательного модуля гиперболической кривой», Rock and Soil Mechanics , том. 29, нет. 7, стр. 1987–1992, 2008.

    Просмотр по адресу:

    Google Scholar

13. Акбас С.О. и Кулхави Ф.Х. Осевое сжатие фундаментов в несвязных грунтах. I: поведение при нагрузке», Journal of Geotechnical and Geoenvironmental Engineering , vol. 135, нет. 11, стр. 1562–1574, 2009.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

14. Л. К. Ивана, С. Н. Власта, М. Предраг, «Прямой метод определения малозаглубленных осадок фундаментов», Градевинар , том. 69, нет. 6, стр. 467–477, 2017.

    Просмотр по адресу:

    Google Scholar

15. Юань В. Х., Лю К., Чжан В., Дай Б. Б. и Ван Ю. «Динамическое моделирование обрушения откоса при больших деформациях» с использованием метода конечных элементов сглаженных частиц», Landslides , vol. 17, pp. 1591–1603, 2020.

    Посмотреть по адресу:

    Google Scholar

16. W. H. Yuan, HC Wang, K. Liu, W. Zhang, D. Wang, and Y. Wang, «Analysis of large деформационно-геотехнических задач с использованием неявного метода обобщенной интерполяции материальных точек» Журнал Чжэцзянского университета НАУКА A , том. 22, нет. 11, стр. 909–923, 2021.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

17. WH Yuan, JX Zhu, K. Liu, W. Zhang, BB Dai и Y. Wang, «Динамический анализ задач большой деформации в насыщенных пористых средах методом конечных элементов сглаженных частиц», Computer Methods в прикладной механике и технике , том. 392, нет. 3, статья 114724, ст. 124, 2022.

    Просмотр:

    Сайт издателя | Google Scholar

18. Б. С. Юань, М. Дж. Чен, В. Дж. Чен, К. З. Луо и Х. З. Ли, «Влияние относительной жесткости сваи-грунта на деформационные характеристики поперечно нагруженной сваи», Достижения в области материаловедения и инженерии , том . 2022 г., идентификатор статьи 4913887, 13 страниц, 2022 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

19. Б. С. Юань, В. Дж. Чен, Дж. Чжао и др., «Добавление щелочных растворов и волокон для армирования каолинитсодержащего гранитного остаточного грунта», Прикладная наука о глине , том. 228, 2022.

    Просмотр по адресу:

    Google Scholar

20. Б. С. Юань, В. Дж. Чен, Дж. Чжао, Ф. Ян, К. З. Луо, Т. Ю. Чен, «Влияние органических и неорганических модификаторов на физические свойства гранитной остаточной почвы», Достижения в области материаловедения и инженерии , том.

    No related posts.