Расчет диагонали онлайн калькулятор: Калькулятор диагоналей

Профессиональные строительные онлайн калькуляторы

Сервис расчета строительных материалов, строительные калькуляторы и конструкторы.
Бесплатный онлайн сервис. Более 50 видов расчета.

У нас Вы можете сделать бесплатно: Расчет размеров и углов стропил, Расчеты количества материалов для двускатной крыши, Расчеты количества материалов для односкатной крыши, Расчеты количества материалов для мансардной крыши, Расчеты стропильной системы шатровой крыши, Расчеты деревянной стропильной фермы, Расчет размеров прямой лестницы, Расчет размеров поворотной лестницы на 90 градусов, Расчет размеров поворотной лестницы с поворотными ступенями на 90°, Расчет лестниц с поворотом на 180 градусов, Расчет размеров поворотной лестницы с поворотными ступенями на 180 градусов, Расчет размеров лестницы с тремя пролетами и ровными площадками, Расчет размеров лестницы с тремя пролетами и поворотными ступенями, Расчет размеров винтовой лестницы, Расчет размеров прямой металлической лестницы, Расчет размеров сварной металлической лестницы с тетивой зигзаг, Расчет размеров металлической лестницы с поворотом на 90 градусов, Расчет размеров металлической лестницы с поворотом на 90 градусов и тетивой зигзаг, Расчет размеров металлической лестницы с поворотом на 180 градусов, Расчет размеров металлической лестницы с поворотом на 180 градусов и тетивой зигзаг, Расчет размеров и количества материалов прямой бетонной монолитной лестницы, Расчет количества стройматериалов для ленточного фундамента, Расчет количества материалов для столбчатого фундамента с ростверком, Расчет материалов для фундаментной плиты, Расчет материалов для изготовления бетонных колец, Расчет количества бетонной тротуарной плитки, брусчатки для дорожки или площадки, Расчет диагонали для разметки фундамента, Расчет диагонали, Расчет количества бетонной тротуарной плитки, брусчатки для дорожки или площадки, Расчет состава бетона, Калькулятор объемов пиломатериала, Калькулятор арматуры, Расчет керамической плитки, Расчет перегородок из гипсокартона, Расчет количества материалов сруба из оцилиндрованного бревна, Расчет материалов стен, Расчет материалов заборов, Расчет кирпичного забора, Расчет арки для забора из штакетника, Расчет материалов для устройства пола, Расчет материалов для наливного пола, Расчет козырька, Расчет площади сложного участка, Расчет объемов земляных работ, Расчет объема траншеи или канавы, Расчет рулонного газона, Расчет бассейна, Расчет объема труб, Расчет объема жидкости в цистерне, Расчет объема жидкости в бочке, Расчет объема жидкости в прямоугольной емкости, Расчет объема песка или гравия в куче, Расчет теплицы, Расчет полукруглой теплицы, Расчет размеров хомута, Калькулятор кредита, Конструктор шкафа-купе

—————————————— Было полезно? Поддержите проект?! ——————————————-

Если Вам понравился данный материал, пожалуйста, посоветуйте его своим друзьям в социальных сетях с помощью кнопок расположенных ниже.

При копировании материала на другие сайты ссылка на наш сайт как источник обязательна, потому, как даже в сети можно и нужно оставаться вежливыми людьми.

Мы рады видеть Вас на нашем сайте!

Диагональ прямоугольника

как правильно и точно разметить фундамент для дома своими руками. Несколько способов разметки, примеры и схемы.

Скачать, сохранить результат

Выберите способ сохранения

• Вы можете сохранить результат расчёта в формате PDF на ваше устройство.

• Распечатайте результат расчёта конструкции на бумагу любого формата.

• Отправьте результат расчета в формате PDF на ваш е-мейл.

Расчет диагоналей для разметки фундамента

Укажите необходимые размеры в миллиметрах

X – длина фундамента

Y

– ширина фундамента

Возможности программы.

Расчет диагонали для разметки фундамента или стен.

Используется для установления точного угла в 90 градусов.

Онлайн калькулятор

Посчитать чему равна диагональ (d) любого прямоугольника (в том числе и квадрата) можно зная длины его сторон (a и b).

Просто подставьте их в калькулятор и получите результат.

Чему равна диагональ прямоугольника если сторона

a = ,

а сторона

b = ?

Ответ:

d

=

Теория

Чему равна диагональ прямоугольника d если известны длина стороны a и длина стороны b?

Формула

d = √a2 + b2

Пример

Если сторона a = 10 см, а сторона b = 5 см, то:

d = √102 + 52 = √100 + 25 ≈ 11.18 см

Необходимость расчета диагонали фундамента

При неверном расчете диагонали все дальнейшее строительство будет расходиться с планом

Проект предполагает подбор конструктивных элементов точно в размер, чтобы при строительстве не возникало перекосов.

Длина балки или плиты перекрытия берется с требуемой глубиной опирания, которая принимается по конструктивному расчету. Во время разметки фундамента нужна предельная точность, т.к. отклонение в размерах повлечет расхождение вертикальных конструкций.

Горизонтальные элементы могут не влезть в проектное положение или вываливаться из монтажного пространства, поэтому потребуется перерасчет длины, а также других показателей.

Правильная разметка основания ведет к приятным бонусам при возведении здания:

• простота строительства стен и применения сборных элементов;
• соблюдение предусмотренной проектом экономии средств и материалов;
• сооружение объекта без отклонений от проекта.

Перед тем как вымерить диагональ фундамента, нужно выровнять строительную площадку, чтобы удобно было размечать линии на местности. Почти всегда строительные конструкции и материалы от утеплительных матов до досок и стеновых щитов имеют прямые углы, поэтому фундамент также размечают с учетом этих требований.

Если диагонали прямоугольника оказываются равными, геодезист выполнил идеальную разметку. Если диагонали неодинаковые, спроектирован не прямоугольник. Но у равнобедренной трапеции также получаются диагонали одинаковой длины, поэтому проверяют стороны угла по принципу золотого сечения с помощью длинного шнура и рулетки.

Калькулятор для расчета диагонали прямоугольника зная стороны

прямоугольник

Об этой статье

Эту страницу просматривали 461 902 раза.

Общие правила для любого фундамента

Выбираем точку отсчета. Первую сторону нашего фундамента нужно привязать к какому-нибудь объекту нашего участка.

Пример. Сделаем так, чтобы наш фундамент (дом) был параллелен  одной из сторон забора.  Следовательно, первую бечевку натягиваем равноудалено от этой стороны забора на нужное нам расстояние.

Построение прямого угла (90⁰). В качестве примера будем рассматривать прямоугольный фундамент, в котором все углы максимально близки к 90⁰.

Существует несколько способов как это сделать. Мы рассмотрим 2 основных.  © www.gvozdem.ru

Способ 1. Правило золотого треугольника

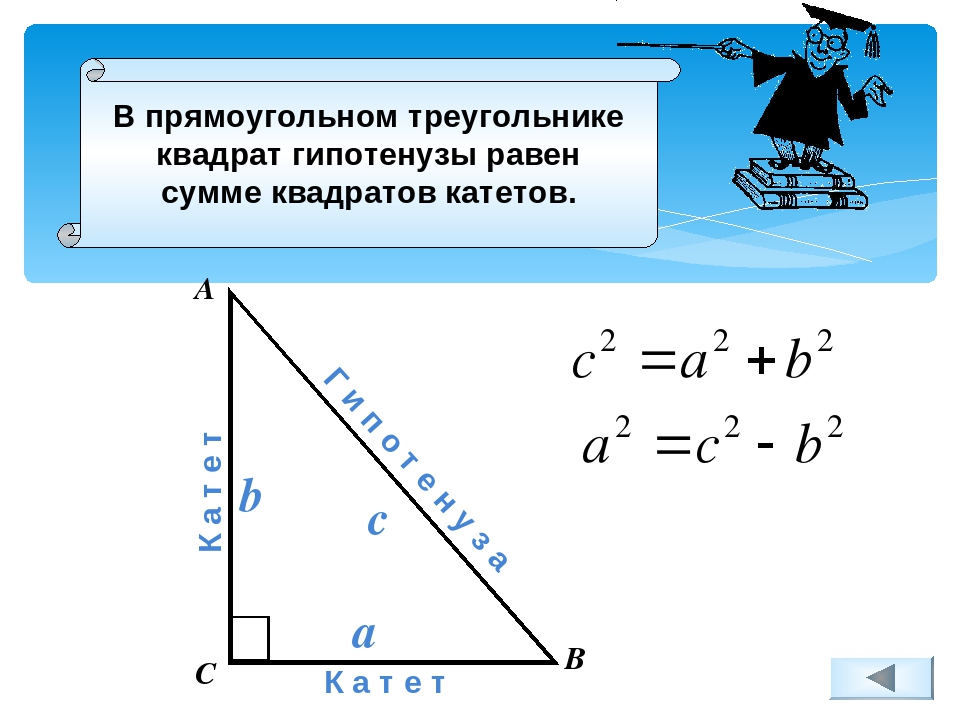
Для построения прямого угла будем применять теорему Пифагора.

Формула   

Чтобы не углубляться в геометрию попробуем описать проще.  Чтобы между двумя отрезками a и b сделать угол в 90⁰ нужно сложить длины этих отрезков и вывести корень из этой суммы. Получившиеся число будет являться длинной нашей диагонали соединяющей наши отрезки.  Очень просто расчет сделать с помощью калькулятора. 

Обычно при разметке фундамента берут размеры сторон, чтобы при выведении из корня получалось целое число. Пример: 3х4х5; 6х8х10.

Если у вас есть рулетка, то в целом проблем не возникнет, если вы будете брать отрезки отличные от общеиспользуемых. Например: 3х3х4,24; 2х2х2,83; 4х6х7,21

Если измерения мы производили в метрах, то значения получаются очень даже понятными: 4м24см; 2м83см; 7м21см.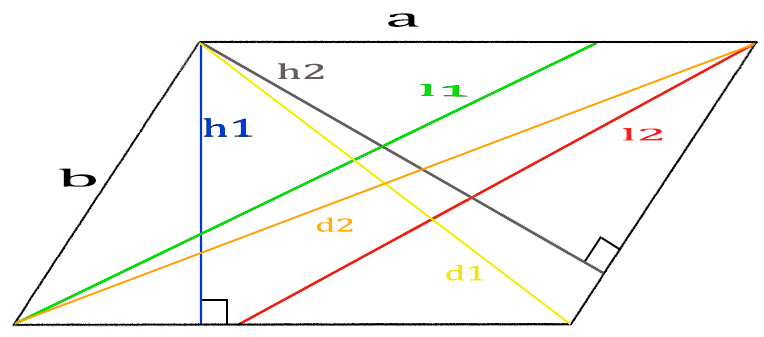

Калькулятор

Также стоит отметить, что измерения можно производить в любых системах измерения длины главное использовать известное нам соотношение сторон: 3х4х5 метра, 3х4х5 сантиметра и т.п. То есть, если даже у вас нет инструмента для измерения длины, то можно взять, например, рейку (длина рейки не имеет значения) и померить ей (3 рейки х 4 рейки х 5 реек).

Теперь давайте посмотрим как это применить на практике.

См. также

Посчитать площадь прямоугольника

Посчитать периметр прямоугольника

Правильный расчет диагонали фундамента

После изучения плана основания нужно приступать к разметке одной из сторон. Это может быть боковая часть, фасадная или задняя, в данном случае это не является важным условием, т.к. принимается во внимание только ориентирование направления.

Длина фундаментной стены не учитывается, можно взять на 1,0 метр больше от места предстоящих углов. В этих точках забивают колья, и натягивают шпагат.

Запас по длине дается, чтобы при копке траншеи не вытащить колышек, и он остался для обозначения направления стороны.

Колышки заменяют доской длиной 1 – 2 метра с прибитыми кольями в торце. Привязанный к ним шнур можно оперативно передвигать из стороны в сторону при необходимости. Такое приспособление для работы называют обноской, оно позволяет расчертить участок с точностью до нескольких миллиметров.

Порядок работы:

• После натяжки шпагата находят точку отсчета по длине и определяют угол фундамента, на шпагате в этой точке цепляют прищепку или забивают кол в грунт, так появляется 2 угла.
• Идентично поступают с перпендикулярной стороной и определяют направление.
• Перед тем как рассчитать диагональ прямоугольного треугольника, по сторонам откладывают 3 и 4 равные части, отмечают их на шпагате (например, 3 и 4 метра).
• Зависимость расстояния между отмеченными точками такова, что гипотенуза должна быть равна пяти частям (5 метров) и не отличаться даже сантиметром, иначе пойдет скос.

Сразу трудно получить правильный результат разметки. Расстояние меньше пяти частей будет означать острый угол, а больше — говорить о величине, превышающей 90°.

Выравнивание величины прямоугольника

В прямоугольнике все углы должны равняться 90°, иначе получится неравнобедренная фигура с перекосами стен. Абрис фундамента имеет наружную и внутреннюю сторону, поэтому требование к прямоугольности касается обоих контуров. Легче всего выровнять величину для дома простой прямоугольной формы, который имеет четыре стены.

Иногда фундаменты в плане имеют сложное строение, например, делаются дополнительные монолитные ленты под пристройку или веранду, а каминный зал рассматривается как вынесенное помещение. В таком случае разметка усложняется тем, что площадь дома будет складываться из отдельных прямоугольников, которые размечаются отдельно.

Каждая фигура после распланировки поверяется на соответствие с другими частями и между составными элементами также устанавливаются прямые углы. Первоначальная сторона привязывается к какой-нибудь основе на местности, которая выглядит прямолинейно. Это может быть ограда, забор, трамвайные пути или бордюр асфальтированной трассы. От этой линии откладывается одинаковое расстояние для обозначения первой стороны искомого плана фундамента.

После окончательной разметки нужно правильно рассчитать диагональ и сравнить расстояние между первой-третьей и второй-четвертой вершиной прямоугольника на местности. Должны получиться идеально одинаковые расстояния. Проверяют и длину противоположных сторон, которые также должны быть равны.

( 1 оценка, среднее 5 из 5 )

Расчет диагоналей параллелограмма

Данный калькулятор специально разработан для нахождения диагоналей четырехугольника ( а именно параллелограмма) по углу и двоим сторонам, которые и делают данный угол.

Для начала давайте же вспомним теорему косинусов, которую мы и используем для данной задачки:

И так:

c2 = a2 + b2 — 2abcosℽ

Сначала нам нужно по теореме косинусов рассчитать диагональ (d1). Дальше, так как в параллелограмме сумма 2 углов = 180 градусов, то не трудно высчитать второй угол. Следующим шагом по той же самой теореме косинусов находим уже вторую диагональ (d2). Ну, а дальше, по старой схеме находим все остальные углы. Чтобы найти углы между диагоналями — нужно помнить, что тут уже сумма 3-х углов = 180 градусов.

Как видите, если разобраться, то нет ничего трудного.



The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 . . %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

Su

Mo

Tu

We

Th

Fr

Sa

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v. d.

z.d.

yes

no

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

minutes

minutes

minute

minutes

minutes

minutes

minutes

minutes

minutes

minutes

minutes

minutes

minutes

hour

hours

hours

hours

hours

hours

hours

hours

hours

hours

hours

days

day

day

day

day

days

days

days

days

days

days

days

month

month

month

month

months

months

months

months

months

months

months

year

of the year

of the year

of the year

years

years

years

years

years

years

years

ago

%1 minutes ago

%1 minutes ago

%1 minutesу ago

%1 minutes ago

%1 minutes ago

%1 minutes ago

%1 minutes ago

%1 minutes ago

%1 minutes ago

%1 minutes ago

%1 minutes ago

%1 minutes ago

%1 minutes ago

%1 hour ago

%1 hours ago

%1 hours ago

%1 hours ago

%1 hours ago

%1 hours ago

%1 hours ago

%1 hours ago

%1 hours ago

%1 hours ago

%1 hours ago

%1 days ago

%1 day ago

%1 day ago

%1 day ago

%1 day ago

%1 days ago

%1 days ago

%1 days ago

%1 days ago

%1 days ago

%1 days ago

%1 days ago

%1 month ago

%1 month ago

%1 month ago

%1 month ago

%1 months ago

%1 months ago

%1 months ago

%1 months ago

%1 months ago

%1 months ago

%1 months ago

%1 year ago

%1 of the year ago

%1 of the year ago

%1 of the year ago

%1 years ago

%1 years ago

%1 years ago

%1 years ago

%1 years ago

%1 years ago

%1 years ago

Диагонали параллелограмма

 Второй угол параллелограмма:

 Угол между d1 и d2:

 Угол между d1 и a:

 Угол между d1 и b:

 Угол между d2 и a:

 Угол между d2 и b:

Площадь параллелограмма, онлайн калькулятор

Наш онлайн калькулятор позволяет вычислить площадь параллелограмма тремя способами: через основание и длину высоты, через диагонали или через две стороны и угол между ними.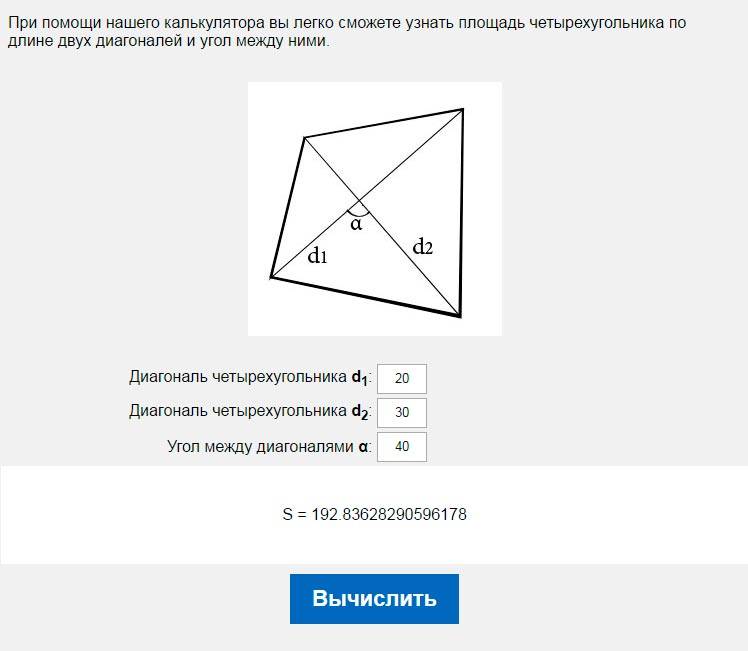 Для того чтобы найти площадь параллелограмма выберите подходящий способ, заполните все нужные поля и нажмите кнопку «Вычислить», калькулятор выдаст ответ и подробное решение!

Введите данные для расчета площади  

Выберите cпособ расчета площади:

через основание и высоту через две стороны и угол через две диагонали

Формула через основание и высоту:

Решили сегодня: раз, всего раз

Понравился сайт? Расскажи друзьям!

Как найти площадь параллелограмма

Площадь наклоненного прямоугольника – параллелограмма узнать не так сложно, как может показаться с первого взгляда. В разных заданиях указываются разные значения, известные изначально. Именно поэтому наш онлайн калькулятор позволяет посчитать площади данного многоугольника несколькими способами:

1. Через основание и высоту параллелограмма;
2. По имеющимся значениям двух сторон и угла между ними;
3. Через две диагонали и угол между ними.

Благодаря нашему сервису вас не надо долго и муторно искать информацию по данным формулам, особенно, если она вам нужна только сегодня и только сейчас. Лучше сэкономить время на подсчет и довериться нашему онлайн калькулятору.

Введите имеющиеся у вас значения в отведенные для этого поля и нажмите на «Вычислить». Ваш результат будет готов до того, как вы уберете руку от клавиатуры, что ценят студенты, школьники и люди, чья профессия требует постоянного подсчета некоторых площадей – строители, архитекторы, монтажники и т.д.

Калькулятор расчета площади прямоугольника

Полезный калькулятор для школьников и взрослых позволяет быстро вычислить площадь прямоугольника по двум его сторонам.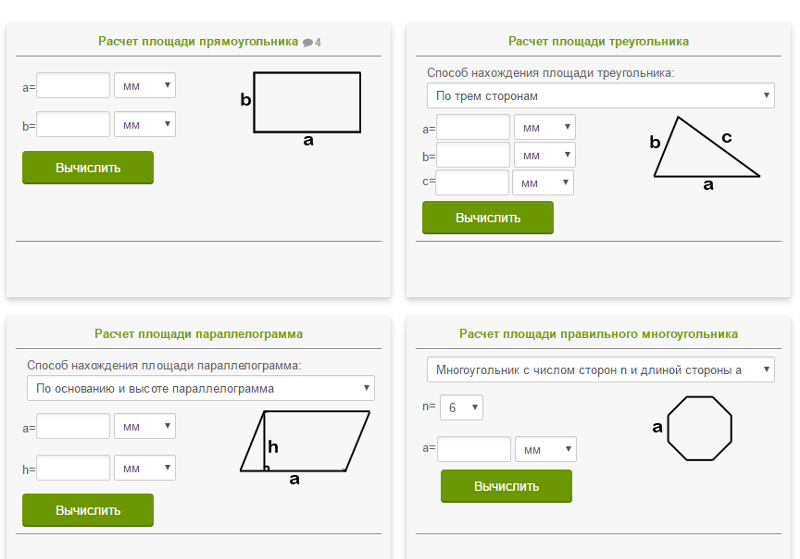 Подобный расчет мы часто производим не только в рамках школьного курса геометрии, но и в  повседневной жизни. Например, если нужно посчитать площадь комнаты при ремонте квартиры, для расчета необходимого количества материалов.

Удобная навигация по статье:

Как рассчитать площадь прямоугольника

Прямоугольником принято называть геометрическую плоскую фигуру, которая имеет параллельно расположенные противоположные стороны при углах в 90 градусов. В качестве длины этой геометрической фигуры выступает величина, которая имеет большую сторону. При этом, за ширину принимается величина меньшей стороны. Для правильного вычисления площади прямоугольника Вам необходимо знать определённые параметры, которыми обладает данная фигура. В их числе:

• диагональ;
• ширина;
• так называемый угол наклона к одной из сторон диагонали;
• длина.

Таким образом, произвести расчёт площади прямоугольника можно различными способами.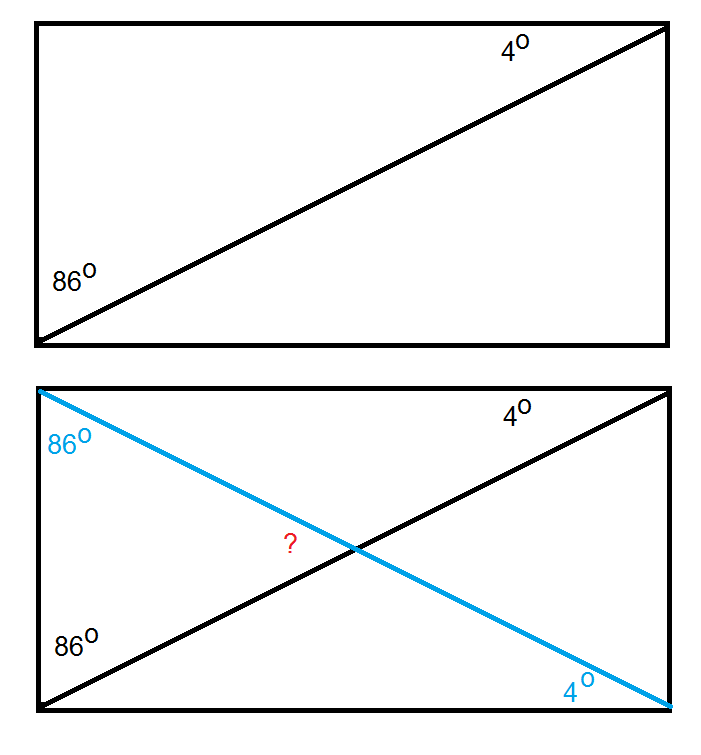 Всё зависит от количества информации о фигуре, а именно, какие величины нам точно известны.

Как вычислить площадь прямоугольника, имея линейные параметры его сторон?

Давайте в качестве обозначения длины прямоугольника будем использовать букву «а», для его ширины – букву «b», а площадь геометрической фигуры обозначим буквой «S». Согласно этому, наша формула будет выглядеть следующим образом: S = a x b.

Зная линейные параметры прямоугольника, можно легко определить его периметр последующей формуле: P = 2(a + b), где в качестве обозначения периметра мы используем букву «P».

Как можно вычислить площадь прямоугольника, зная величину одну из его сторон и диагональ?

Как нам известно, диагональ делит любой прямоугольник на два так называемых прямоугольных треугольника. Давайте присвоим диагонали индекс «с», а длину стороны обозначим буквой «а». Теперь необходимо произвести следующий порядок действий:

1. для начала необходимо найти длину неизвестной стороны. Для этого мы используем формулу Пифагора: b = V c2 – a2.
2. После этого, нам следует определить площадь нашей основной геометрической фигуры (прямоугольника) как площадь треугольника, умноженную на два: Sтр = ½ (а х в).
3. Согласно вышеописанной схеме расчёта площадь прямоугольника в данном случае будет равна: S = 2 x Sтр = а х в.

В том случае, если нам известны периметр прямоугольника, а также длина одной из его сторон, то площадь этой геометрической фигуры можно вычислить, определив длину второй стороны (b = (P – 2xa), по такой формуле: S = a x b.

Если же нам известны размер диагонали прямоугольника, а также угол между стороной и самой диагональю, то площадь можно вычислить при помощи следующих тригонометрических функций: Sтр = ½ х с2 х sinФ х cosФ.

При этом, общая площадь в данном случае будет составлять S = 2 x Sтр.

Площадь прямоугольника. Видео-урок.

Площадь ромба: онлайн калькулятор, формулы, примеры решений

Ромб — это четырехугольник, все стороны которого одинаковы. Ромб представляет собой частный случай параллелограмма, а квадрат — частный случай ромба. Следовательно, каждый квадрат — это ромб, а каждый ромб — параллелограмм.

Геометрия ромба

Термин «ромб» с греческого языка означает «бубен», который в древности выполняли в виде четырехугольника, а не круга. Ромб — равносторонний параллелограмм с неравными углами. Любой равносторонний четырехугольник, который имеет два острых и два тупых угла может называться ромбом. Таким образом, ромб в отличие от квадрата является косоугольником. Параллелограмм будет считаться ромбом, если фигура соответствует хотя бы одному из условий:

• две смежные стороны равны, соответственно, равны все стороны;
• диагонали фигуры пересекаются под прямым углом;
• все высоты косоугольника равны;
• диагонали делят четырехугольник на 4 одинаковых прямоугольных треугольника;
• одна из диагоналей является биссектрисой для внутренних треугольников.

Данная фигура в своей классической форме не часто встречается в реальной жизни. Чаще всего ромбы можно найти в металлообработке: пластины резцов различных инструментов имеют именно ромбовидную форму. Кроме того, ромбические элементы встречаются в архитектуре и строительстве, а наиболее очевидным примером реального ромба является тротуарная плитка. Встречая ромбы в реальности, вам может понадобиться определить площадь данной фигуры для решения практических задач.

Площадь ромба

Площадь ромба — это плоскость, ограниченная периметром фигуры. Площадь такого четырехугольника можно найти шестью способами, используя для расчетов такие параметры как величины углов, длины сторон или диагоналей. Наиболее простая формула для определения площади ромбовидной фигуры оперирует диагоналями. Диагональ ромба — это отрезок, который соединяет вершины противоположных углов косоугольника. Зная длину диагоналей ромба, вы можете вычислить площадь по следующей формуле:

S = 0,5 d1 × d2

Для определения площади ромба вы можете использовать наш онлайн-сервис, который позволяет найти не только площадь или периметр фигуры, но и определяет ее углы, длину сторон и высоту. Для вычислений вам потребуется ввести в форму два параметра на выбор:

• две диагонали;
• высоту и сторону.

Зная эти два значения, программа рассчитает все остальные свойства ромба, которые могут вам понадобиться при решении практических задач. Рассмотрим пару примеров.

Примеры из реальной жизни

Плитка

Ранее мы выяснили, что тротуарная плитка — это самый банальный пример ромбических фигур в реальной жизни. Допустим, есть участок, который вы хотите замостить такой плиткой. Для определения необходимого количества плитки, которое нужно закупить, вам потребуется узнать два параметра: площадь участка и площадь одного элемента тротуарного покрытия. Пусть площадь участка составляет 20 квадратных метров, а диагонали плитки равны 20 см и 10 см. Для правильного расчета необходимо выразить длину диагоналей в метрах (0,2 и 0,1 м) и ввести их в поля «Диагонали». Вы получите результат в виде:

S = 0,01

Следовательно, площадь одного элемента составляет 0,01 квадратных метров, и вам понадобится 2 000 маленьких ромбов для обустройства участка.

Геральдика

Большая часть гербов исполняется на ромбовидных геральдических щитах. Если вы захотите сделать собственный ромбовидный герб для фестиваля исторической реконструкции, то вам понадобится узнать, сколько ткани нужно для его создания. Вы можете прикинуть только длину стороны и высоту ромба. Пусть высота фигуры составляет 0,3 м, а сторона — 0,5 м. Тогда площадь герба будет равна:

S = 0,15

Таким образом, для создания герба вам понадобится 0,15 квадратных метров ткани.

Заключение

Ромб не занимает в реальной жизни человека значимое место: фигура встречается нечасто, в основном в машиностроении, архитектуре и дизайне. Для решения практических задач или школьных заданий вы можете воспользоваться онлайн-калькулятором, который мгновенно выдаст вам не только правильный результат, но и вычислит углы, стороны и высоту ромба.

Калькулятор расчета вагонки

Популярность применения вагонки возрастает с каждым днем. И для этого есть веские основания:

• вагонка – универсальный материал, который подходит для отделки как внешних, так и внутренних стен;
• стоимость делает ее доступной для широких масс населения;
• богатый ассортимент используемых материалов при изготовлении, позволяет применять ее в самых разных дизайнерских проектах.

Но какая бы вагонка не была выбрана, ошибки в расчете нужного количества материала, могут не только нарушить текущий процесс ремонта, но и существенно изменить предполагаемый результат отделки.

Выбор древесины

На сегодняшний день строительный рынок наполнен разнообразными вариантами отделочных материалов, поэтому для новичка в делах ремонта и стройки, выбор вагонки может стать серьезным испытанием.

Основное, с чем покупатель должен идти на рынок, это понятие точного значения нужного количества материала. Такой подход поможет предотвратить некоторые неудобные ситуации. Ведь покупка лишних материалов приводит не только к потере денежных средств, но и времени, на его возможный возврат.

Важно! Выбирая деревянную вагонку, особое внимание стоит уделить породе дерева, из которого она изготовлена. Наиболее распространенные варианты – это лиственные и хвойные породы дерева.

Рассмотрим наиболее часто используемые в производстве вагонки виды деревьев:

1. Сосна. Отличается высокими показателями прочности, чем и привлекает потребителя. Однако нужно знать, что сосновая вагонка быстро теряет свой первоначальный цвет, если ее не обработать защитными лаками или морилкой.
2. Дуб. Красивая структура дерева, которая практически не поддается гниению, делает такую вагонку лидером в рейтинге популярности отделочных материалов. Ее единственный минус – высокая цена, доступная не всем.
3. Ясень. Его используют не очень часто потому как обработка такой древесины занятие довольно трудоемкое и затратное. Но при этом древесина ясеня очень прочная и при сушке не меняет свою структуру и форму.
4. Липа – это идеальный вариант для обустройства парилок в бане или сауне. Она отлично сохраняет тепло, не выделяя при этом вредные для здоровья человека масла смолы.

Сорта древесины

Качество пиломатериала и как следствие конечный вид изделия, существенно влияет на цену вагонки.

Различают четыре основных сорта древесины, которые могут влиять на показатель стоимости:

• категория «Экстра». Это наивысший класс древесины, который на своей поверхности не имеет сучков, трещин и других дефектов;
• класс «А» присваивается древесине, у которой может быть один два сучка на один погонный метр доски;
• класс «В» предполагает, что на поверхности дерева имеются дефекты темного цвета, диаметром до 1см;
• класс «С» присваивается самой низкопробной древесине, из которой производят вагонку соответствующей цены и качества.

Произвести расчет необходимого количества материала не сложно. Если возникнут затруднения, на помощь всегда придет продавец товара. Главное все расчеты произвести вовремя, до совершения сделки. Это поможет сохранить денежные средства и предотвратить ситуацию, когда после ремонта остается очень большое количество обрезков.

Запас вагонки, конечно же, должен быть, но в разумных пределах. Как правило, специалисты рекомендуют к расчетному значению необходимого количества материала прибавлять 10-15 % запаса.

Важно! При выборе выгонки, учитывать функциональное предназначение помещения, где будут проходить отделочные работы.

Какими единицами реализуется вагонка

Вагонка в основном продается кубометрами, что может создавать некоторые неудобства при расчете нужного количества материала. Для большего удобства стоит запомнить какую приблизительно площадь может укрыть вагонка определенного размера:

• панель, размеры которой составляют 6000*200*8 мм, займет собой площадь 1,2 м2;
• если параметры вагонки составляют 6000*250*5, то размер площади будет 1,5 м2;
• панель с габаритами 2600*148*6 укроет площадь в 7,07 м2.

Как видно габариты материала учитывают показатель толщины. Если вагонка продается поштучно, то показатель толщины никакого значения не имеет, и не применяется при выполнении расчета.

Однако в случае продажи материала в единицах объема, параметр толщины оказывает существенное влияние на конечный результат при расчете нужного количества вагонки.

Расчет количества вагонки

Расчет количества вагонки производится по следующему алгоритму:

Определяем общую площадь для обшивки:

S = (2АН +2ВН) – (ahn + bh1n1), где А – длина помещения; Н – высота комнаты; В – ширина комнаты; a – ширина окна; b – ширина двери; h, h2 – высота окна и двери; n, n1 – количество окон и дверей.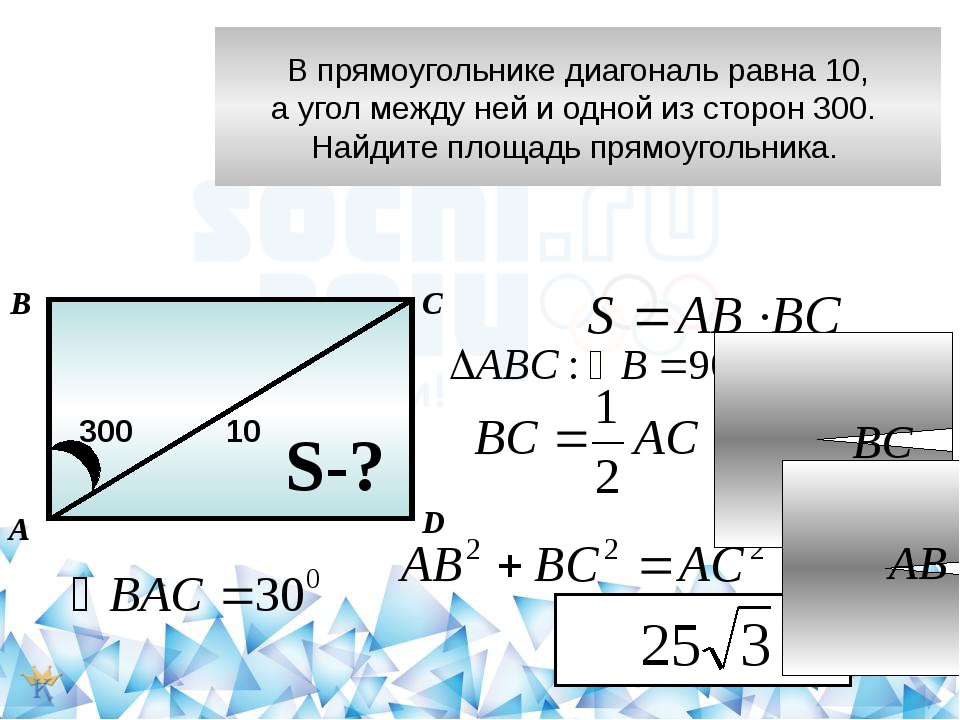

Если учитывается площадь потолка, то формула расчета выглядит следующим образом:

S= (2AH + 2BH +AB) – (ahn + bh2n1).

Определяем площадь вагонки для мансарды, потолок которой представлен двумя поверхностями и вертикальным фронтом без переборок:

S = 2AB + 2b (4A2-b2)/4, где А – расстояние от конька до основания ската.

Если требуется расчет количества вагонки для мансарды с переборками, формула выглядит следующим образом:

Площадь = 2AB + 2b (4A2-b2)/4 + Ph, где Р является показателем периметра переборок, h – высота стенки.

Вычислить площадь одной панели можно путем несложных математических вычислений. Для определения площади одной панели необходимо длину этой панели умножить на ширину. В полученном результате необходимо вычесть площадь паза, который не является элементом поверхности обшивки.

Для расчета требуемого количества материала в штуках, нужно общую площадь обшивки поделить на площадь одной панели.

Расчеты можно проводить вручную, но этот процесс, как правило, занимает достаточно большое количество времени и сил. Ускорить его и сделать более легким помогут специальные компьютерные программы онлайн калькуляторов. Как показывает практика, итоговые значения при использовании такого способа не будут существенно отличаться от тех, которые бы получились при ручном вычислении.

Заключение

Расчет необходимого количества вагонки для обшивки любых поверхностей вашего дома выполнить не сложно. Расчет можно осуществить самостоятельно вручную, или воспользоваться компьютерными программами онлайн калькулятора. Для этого нужно только знать точные значения основных параметров поверхности: ширину, высоту, длину, а также толщину вагонки.

Точность вычислений не только сохранить бюджет ремонта от лишних трат, но и избавит от большого количества обрезков. Но все-таки вычисляя значение нужного количества вагонки, помните, дробное значение всегда округляют в большую сторону и прибавляют к нему до 15% стратегического запаса материала.

После того, как выполнен расчет необходимого количества вагонки, можно приступать к ее монтажу

диагоналей прямоугольника с калькулятором

диагоналей прямоугольника с калькулятором — Math Open Reference

Попробуй это Перетащите любую вершину прямоугольника ниже. Он останется прямоугольником, и будет рассчитана длина диагонали.

Прямоугольник имеет две диагонали. Каждый из них отрезок нарисованный между противоположным вершины (углы) прямоугольника. Диагонали обладают следующими свойствами:

• Две диагонали конгруэнтные (одинаковой длины).На рисунке выше нажмите «показать обе диагонали», затем перетащите оранжевую точку в любую вершину прямоугольника и убедитесь, что это так.
• Каждая диагональ делит пополам другой. Другими словами, точка, где диагонали пересечь (крест), делит каждую диагональ на две равные части
• Каждая диагональ делит прямоугольник на две части. равные прямоугольные треугольники. Поскольку треугольники совпадают, они имеют одинаковую площадь, и каждый треугольник имеет половину площади прямоугольника
.

Длина по диагонали

На рисунке выше нажмите «Сброс».Как видите, диагональ прямоугольника делит его на две части. прямоугольные треугольники, BCD и DAB. Диагональ прямоугольника — это гипотенуза этих треугольников. Мы можем использовать Теорема Пифагора чтобы найти длину диагонали, если мы знаем ширину и высоту прямоугольника.

В виде формулы: где:
w — ширина прямоугольника
h — высота прямоугольника

Калькулятор

Используйте калькулятор выше, чтобы вычислить свойства прямоугольника.

Введите длину двух сторон, и оставшаяся часть будет рассчитана. Например, введите длину двух сторон. Будут найдены площадь, периметр и длина диагонали.

Что попробовать

1. На рисунке вверху страницы нажмите «сбросить» и «скрыть детали». Затем перетащите углы, чтобы создать произвольный прямоугольник. Рассчитайте длину диагоналей. Нажмите «Показать подробности», чтобы проверить свой ответ.
2. Прямоугольник имеет высоту 12 и диагональ 31.Найдите ширину прямоугольника и используйте анимацию или калькулятор выше, чтобы проверить свой ответ.

Другие темы о многоугольниках

Общие

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с полигонами

Именованные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

Калькулятор диагонали прямоугольника

Прямоугольник — это четырехугольник, в котором все четыре угла составляют 90 ^o , противоположные стороны параллельны и равны по длине

Что такое диагональ у калькулятора прямоугольника?

Прямоугольник — это четырехугольник, в котором все четыре угла составляют 90 ^o , противоположные стороны параллельны и равны по длине, две диагонали имеют равную длину и пересекаются друг с другом в середине.

Онлайн-калькулятор диагонали прямоугольника

Cuemath позволяет вам найти длину диагонали прямоугольника.

Как использовать калькулятор диагонали прямоугольника?

Следуйте инструкциям ниже, чтобы найти длину диагонали прямоугольника.

• Шаг 1: Введите длину прямоугольника.
• Шаг 2: Введите ширину прямоугольника.
• Шаг 3: Нажмите «Рассчитать», чтобы найти длину диагонали прямоугольника.
• Шаг 4: Нажмите «Сброс», чтобы найти длину диагонали прямоугольника для различных наборов длины и ширины.

Что такое диагональ прямоугольника?

Диагональ разрезает прямоугольник на 2 прямоугольных треугольника. В котором стороны равны сторонам прямоугольника и с гипотенузой. Эта гипотенуза диагональна.

Длина диагонали прямоугольника определяется по следующей формуле:

Диагональ прямоугольника = √ (l² + w²)

Здесь «l» обозначает длину прямоугольника, а «w» обозначает ширину прямоугольника.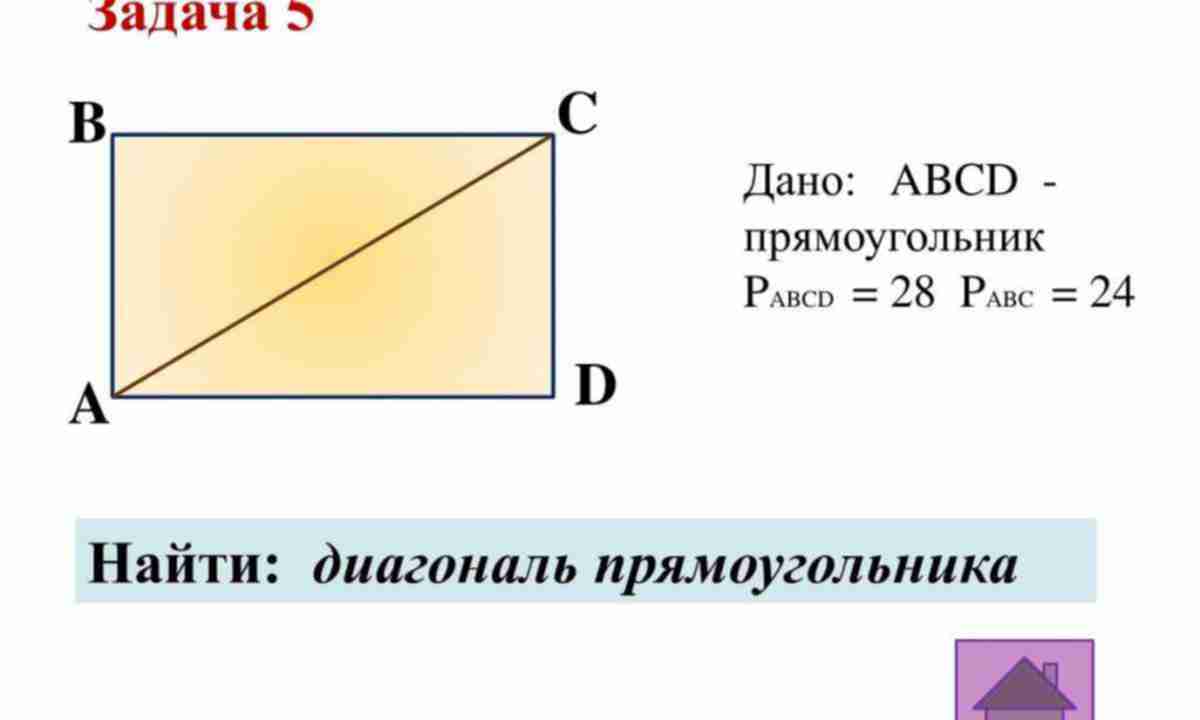

Калькулятор диагонали прямоугольника использует ту же формулу для вычисления длины диагонали прямоугольника.

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

Решенный пример:

Найдите длину диагонали прямоугольника, длина которого 4 единицы, а ширина 3 единицы.

Решение:

Длина прямоугольника = 4 единицы

Ширина прямоугольника = 3 единицы

Подставляя значения длины и ширины в формулу, получаем

Диагональ = √ (l² + w²)

= √ (4² + 3²)

= √ (25²).

= 5 единиц.

∴ Длина диагонали прямоугольника = 5 единиц.

Теперь используйте калькулятор, чтобы найти длину диагонали для следующих прямоугольников с

• Длина = 8 шт. Ширина = 6 шт.
• Длина = 6 шт. Ширина = 8 шт.

Калькулятор прямоугольников

Что такое площадь и периметр прямоугольника?

Четырехугольник с четырьмя равными углами — это прямоугольник. Слово «прямоугольник» происходит от латинского «rectangulus». Это комбинация «rectus», что означает «прямо», и «angulus», что означает «угол».o $$

Длины его сторон обозначены $ a $ и $ b $, а длина диагонали обозначена $ d $. Прямоугольник также называют равносторонним четырехугольником, поскольку все его углы совпадают.
Прямоугольник — это параллелограмм, но параллелограмм не является прямоугольником, потому что в прямоугольнике каждый угол является прямым углом, тогда как в параллелограмме это не так. Это означает, что все свойства параллелограмма можно применить и к прямоугольникам. Напомним, что параллелограмм имеет следующие свойства:

• Противоположные стороны параллелограмма равны;
• Противоположные углы параллелограмма равны;
• Последовательные углы параллелограмма дополняют друг друга;
• Диагонали параллелограмма делят друг друга пополам

Прямоугольник удовлетворяет еще одному свойству:

• Диагонали прямоугольника равны;

Если мы знаем длины сторон прямоугольника, легко вычислить длину диагонали, используя теорему Пифагора. 2} $$

Прямоугольник имеет только две линии симметрии. Эти линии соединяют середины противоположных сторон прямоугольника. Прямоугольник имеет центральную симметрию и вращательную симметрию. Центр симметрии — это точка пересечения диагоналей $ O $.
Расстояние вокруг прямоугольника называется периметром прямоугольника. Обычно обозначается $ P $. Чтобы найти периметр прямоугольника, складываем длины его сторон. Таким образом, периметр прямоугольника длиной $ a $ и шириной $ b $ равен

$$ P = a + b + a + b = 2 \ times a + 2 \ times b = 2 \ times (a + б) $

Площадь прямоугольника или другого многоугольника — это количество квадратных единиц, необходимых для заполнения прямоугольника.2) $ и т. Д.

Работа с площадью и периметром прямоугольника с шагом показывает полный пошаговый расчет для нахождения периметра, площади и длины диагонали прямоугольника с длиной $ 5 \; в $ и шириной $ 10 \; in $ по формулам периметра, площади и длины диагонали. Для любые другие значения для длины и ширины прямоугольника, просто введите два положительных вещественных числа и нажмите кнопку GENERATE WORK. Учащиеся начальной школы могут использовать эту площадь и периметр прямоугольника для создания работы, проверки результатов периметра и площади двумерных фигур или эффективного выполнения домашних заданий.

Онлайн калькулятор: Площадь четырехугольника

Есть несколько способов рассчитать площадь четырехугольника

https://en.wikipedia.org/wiki/File:Tetragon_measures.svg

Изображение: wikipedia

1. Площадь четырехугольника по диагоналям и угол между ними. В этом случае формула будет
   

Калькулятор:

Выпуклый четырехугольник

Точность вычисления

Цифры после десятичной точки: 2

content_copy Ссылка сохранить Сохранить расширение Виджет

2. Площадь четырехугольника с четырьмя сторонами и двумя противоположными углами.В данном случае это будет формула Бретшнайдера
.

,
где s — полупериметр

Калькулятор:

Площадь общего четырехугольника с учетом четырех сторон и двух противоположных углов

Точность вычисления

Цифры после десятичной точки: 2

content_copy Ссылка сохранить Сохранить extension Widget

3. Площадь четырехугольника с учетом четырех сторон и двух диагоналей. В данном случае это будет нетригонометрическая формула Бретшнейдера
.

,
где s — полупериметр

Калькулятор:

Площадь общего четырехугольника с учетом четырех сторон и двух диагоналей.

Точность вычисления

Цифры после десятичной точки: 2

content_copy Ссылка сохранить Сохранить расширение Виджет

4. Площадь четырехугольника с учетом четырех сторон и того факта, что это вписанный четырехугольник. Это частный случай формулы Бретшнайдера (мы знаем, что сумма двух противоположных углов равняется 180), известной как формула Брахмагупты
.

,
где s — полупериметр

Для этого вы можете использовать калькулятор выше, введя произвольные углы, сумма которых равна 180.

Доказательство формул Бретшнайдера можно найти здесь

Стоит отметить, что невозможно найти четырехугольник, учитывая ТОЛЬКО четыре стороны. Вам потребуются дополнительные условия, подобные приведенным выше. Таким образом, по многочисленным просьбам мы создали модельный калькулятор, который вычисляет площади четырехугольника по четырем сторонам — для бесконечного количества четырехугольников. Вы можете найти его в области неправильного четырехугольника с заданными сторонами.

Расчет трапеции — онлайн калькулятор и формула

Рассчитайте длину стороны \ (a \) трапеции
	\ (\ displaystyle a = \ frac {A · 2} {h} -c \)	\ (а = т · 2 -с \)
Рассчитайте длину стороны \ (b \) трапеции
	\ (\ displaystyle b = \ frac {h} {sin (β)} \)	\ (\ Displaystyle b = \ гидроразрыва {h} {грех (γ)} \)
Рассчитайте длину стороны \ (c \) трапеции
	\ (\ displaystyle c = \ frac {A · 2} {h} — a \)	\ (\ Displaystyle с = м · 2 — а \)
Рассчитайте длину стороны \ (d \) трапеции
	\ (\ Displaystyle d = час / грех (α) \)	\ (d = h / sin (δ) \)
Вычислить диагональ \ (e \) трапеции
	\ (\ Displaystyle е = \ sqrt {a ^ 2 + b ^ 2 — 2 · a · b · соз (β)} \)
Вычислить диагональ \ (f \) трапеции
	\ (\ Displaystyle f = \ sqrt {a ^ 2 + d ^ 2-2 · a · d · cos (α)} \)
Вычислить высоту \ (h \) трапеции
	\ (\ displaystyle h = \ frac {2 · A} {a + c} \)	\ (h = b · sin (β) \)
Вычислить среднюю ширину \ (м \) трапеции
	\ (\ Displaystyle м = \ гидроразрыва {а + с} {2} \)	\ (\ Displaystyle м = А / час \)
Вычислить площадь \ (A \) трапеции
	\ (\ Displaystyle А = \ гидроразрыва {(а + с) · ч} {2} \)	\ (А = м · ч \)
Вычислить периметр \ (P \) трапеции
	\ (\ Displaystyle P = a + b + c + d \)
Вычислить угол \ (α \) трапеции
	\ (\ Displaystyle α = asin \ влево (\ гидроразрыва {h} {d} \ right) \)	\ (\ Displaystyle α = 180 — δ \)
Вычислить угол \ (β \) трапеции
	\ (\ Displaystyle β = asin \ left (\ frac {h} {b} \ right) \)	\ (\ Displaystyle β = 180 — γ \)
Вычислить угол \ (γ \) трапеции
	\ (\ Displaystyle γ = 180 — β \)
Вычислить угол \ (δ \) трапеции
	\ (\ Displaystyle δ = 180 — α \)
Вычислить превышение \ (x \) трапеции
	\ (\ Displaystyle х = \ sqrt {d ^ 2-h ^ 2} \)
Вычислить превышение \ (y \) трапеции
	\ (\ Displaystyle у = \ sqrt {b ^ 2-h ^ 2} \)

Калькулятор квадрата фундамента

Этот калькулятор требует использования Javascript и поддерживающих браузеров. Этот калькулятор предназначен для получения результата математического расчета, позволяющего убедиться, что фундамент (или комната, стропильный фундамент или другая 90-градусная конструкция) действительно квадратный и имеет правильную планировку. (Будьте квадратными или ремонтируйте …) Расчет основан на теореме Пифагора. Сведенный к простым строительным терминам, он говорит, что квадрат длины фундамента плюс квадрат ширины фундамента равняется квадрату диагонального расстояния фундамента (от противоположного угла до противоположного угла). В строительной отрасли он также известен как 3-4-5, что означает, что если длина равна 3 (в квадрате = 9), а ширина равна 4 (в квадрате = 16), то диагональ равна 5 (в квадрате = 25).Проверка верна в том, что 9 плюс 16 равно 25, из которых квадратный корень равен 5. Хотя транспортиры и Т-образные квадраты очень полезны, чем больше расстояние для измерения, тем оно точнее. (Если вы не хотите на самом деле измерять, но можете определить с помощью жала, обе диагонали должны быть равны для квадратного фундамента. ) Всего лишь небольшая часть градуса отклонения от 90 градусов, более 20 футов или более, является существенной ошибкой при вычислении. заставляя стены не быть прямыми или квадратными. Немного дополнительных усилий на начальных этапах дает в конечном итоге гораздо более профессиональную структуру. Калькулятор может работать в американской системе футов и дюймов, а также в метрической системе метров. Сначала выберите американскую или метрическую систему счисления. В режиме футов и дюймов (американская система) введите значение футов, обозначенное как футы, а затем дюймы, если они есть, в поле, обозначенное как дюймы. Если у вас есть доля дюйма, вы можете ввести его. Учтите, что это десятичная дробь; например, 0,5 — 1/2 дюйма, а 0,75 — 3/4 дюйма. Если вы не уверены в преобразовании, вы можете использовать наши таблицы преобразования для точности до 64-х долей дюйма в десятичной системе счисления.(Если вы уже знаете, как преобразовать дюймы в десятичную дробь, вы можете просто ввести его как футы. Например, вы можете ввести 5 футов 6 дюймов как 5 в поле футов и 6 в поле дюймов, или просто 5,5 в футах. поле и нет ввода в поле дюймов.) В метрическом режиме используется только первое поле для длины и ширины; система и калькулятор принимают десятичные числа. В американском режиме ответ возвращается в футах, дюймах и строительных дробях (до 64-х), в то время как в метрическом режиме возвращаются метры и десятичные значения.Если вы выполняете более одного расчета, не забудьте между попытками нажимать кнопку «Очистить значения».

Калькулятор равнобедренного треугольника — Расчет высокой точности

[1] 2021/08/06 07:53 Уровень 30 лет / Инженер / Очень /

Назначение

Расчет треугольной плитки рисунка маркетри.

[2] 2021/06/10 15:24 Уровень 30 лет / Инженер / Полезный /

Цель использования

Инженер-химик выполняет некоторые вычисления крутящего момента в машиностроении между двумя руками заданной длины.

[3] 2021/06/04 09:04 Уровень 40 лет / Другое / — /

Цель использования

Создание драгоценного камня бриллиантовой огранки векторной графики

[4] 2021/05/ 06 05:04 Уровень 20 лет / Учитель / Исследователь / Очень /

Цель использования

Модель Lego

[5] 2021/05/04 11:25 До 20 лет / Средняя школа / ВУЗ / аспирант / Very /

Цель использования

Помогает при выполнении домашних заданий (геометрия для старших классов).

[6] 2021/04/25 21:30 Уровень 50 лет / Самозанятые люди / Очень /

Цель использования

Попытка подсчитать, сколько годного к употреблению масла у меня осталось в циклической (горизонтальной! ) бак. Требуется для вычисления углов треугольника по известной гипотенузе (радиус круга) и высоте треугольника (уровень масла). Получилось удовольствие. Осталось еще 195 литров! (заменяем бак).

[7] 2021/04/21 10:12 Уровень 30 лет / Инженер / Очень /

Цель использования

Слишком долго не ходил в школу. Изготовление стола из эпоксидной смолы, необходимого для подрезки стальных ножек, пока смола мокрая. Вырисовал ножки для прямоугольной основы, забыл некоторые геометрические доказательства. Смотрел их и вручную делал расчеты. Проверил с помощью этого калькулятора -> получилось с такими же точными числами и углами. Хороший инструмент для проверки, не ленитесь и полагайтесь на технологии, которые сделают все за вас. Вот почему у нас есть манекены, которые не могут решать математические уравнения Facebook.

[8] 2021/04/17 22:19 60 лет и старше / Пенсионер / Очень /

Назначение

Пошив шторки для горки для муниципального бассейна.Это пирамида, состоящая из 4-х треугольников. Стороны легко измерить, углы нужны.

Комментарий / запрос

Отлично и быстро. Спасибо.

[9] 2021/04/05 04:56 Уровень 40 лет / Другое / Очень /

Цель использования

Рассчитать размер детской палатки для двора 🙂

[10] 2021 / 03/02 23:20 До 20 лет / Старшая школа / ВУЗ / Аспирант / Очень /

Цель использования

быстрее разобраться в вещах

.