Кубатура доски калькулятор: Калькулятор доски для точного расчета количества материала

Содержание

Как рассчитать объем пиломатериалов ⭐️ Глазов-Леспром

Чтобы правильно рассчитать пиломатериал в кубах, который нужен для строительства, используйте простую формулу:
Кубатура = Длина х Толщина х Ширина.

Ширина – по ГОСТ 24454-80 может быть от 75 до 275 мм, а подбирать оптимальное значение нужно с учетом актуализированной версии СП 64.13330.2011;
Толщина – с учетом перечисленных стандартов может варьироваться от 16 до 250 мм;
Длина – варьируется от 1000 до 6000 мм;

Наши консультанты помогут вам произвести расчет объема пиломатериалов, которые требуются для строительства и отделки дома, бани и других сооружений.

Почему важно точно рассчитать количество пиломатериалов?

Пиломатериалы используются везде: в строительной и мебельной сфере, при создании ограждений, тары и прочих полезных вещей. Древесина является отличным тепло- и звукоизолятором, экологически безопасна и универсальна.

Расчет погонажа для крыши позволит вам не переплачивать за ненужное сырье и не ломать голову над тем, как заказать нехватающее количество кубов на кровлю. Вы сэкономите время, финансы и силы, если заранее просчитаете объем лесоматериалов.

Онлайн-калькулятор помогает подсчитать число пиломатериалов. Однако программа не отвечает на вопросы по подсчетам, а консультанты «Глазов-Леспром» помогут разобраться в технических нюансах.

Как узнать, сколько материала потребуется?

Наша компания производит следующие виды пиломатериалов из прочной лиственницы и других пород древесины:

вагонка;
планкен;
имитация бруса;
блок-хаус;
половая, террасная, палубная доска.

Чтобы узнать объем сырья в кубометрах, следует использовать следующие формулы расчета пиломатериалов:

E = W x H x L,

где W – толщина, H – ширина, L – длина. Предварительно нужно перевести миллиметры в метры. В итоге вы узнаете объем доски в метрах кубических – E.

Чтобы рассчитать число бруса в одном кубометре (N), нужно 1 м3 разделить на полученный показатель Е. В результате получится необходимое количество изделий для строительства.

N = 1 / E.

Таблица расчета пиломатериалов для вагонки

Толщина, мм	Ширина, мм	Длина, мм	Количество досок в м3, шт	Объем доски в м3
14	90	3000	264,55	0,00378
14	110	3000	216,45	0,00462
14	138	3000	172,53	0,005796

Таблица расчета для планкена

Толщина, мм	Ширина, мм	Длина, мм	Количество досок в м3, шт	Объем доски в м3
20	90	2000	277,8	0,0036
20	95	2000	263,2	0,0038
20	115	2000	217,4	0,0046
20	120	2000	208,3	0,0048
20	140	2000	178,6	0,0056
20	165	2000	151,5	0,0066
20	190	2000	131,6	0,0076

Сколько половой, террасной, палубной доски в кубе

Толщина, мм	Ширина, мм	Длина, мм	Количество досок в м3, шт	Объем доски в м3
20	110	2000	227,3	0,0044
28	90	2000	198,4	0,00504
28	120	2000	148,8	0,00672
28	140	2000	127,6	0,00784
35	115	2000	124,2	0,00805
35	140	2000	102,1	0,0098
45	115	2000	96,6	0,01035
45	140	2000	79,4	0,0126

Чтобы рассчитать объем пиломатериалов в м2, используйте формулу:

H (ширину) x L (длину) = S (площадь доски).

После этого площадь помещения нужно разделить на полученную площадь лесоматериала. И получится число в штуках, которое необходимо для работы.

Важно! Брать лесоматериалы рекомендуется с запасом 10–20%. Чтобы в случае форс-мажоров в процессе работы вам не пришлось докупать поштучно.

Точный расчет в метрах кубических будет полезен, чтобы:

снизить цену – вы можете купить нужное число погонажа, не переплачивая за лишнее;
правильно подобрать транспорт – чтобы не переплачивать за услуги большегрузов и не делать повторных рейсов.

Обращайтесь в «Глазов-Леспром» за пиломатериалами и помощью в их подборе

Наши менеджеры помогут вам рассчитать пиломатериал. Чтобы вы приобрели ровно столько обрезных и необрезных материалов, сколько нужно для решения задачи.

Собственное производство и складские мощности позволяют нам предлагать изделия из дерева по удобной для клиентов стоимости.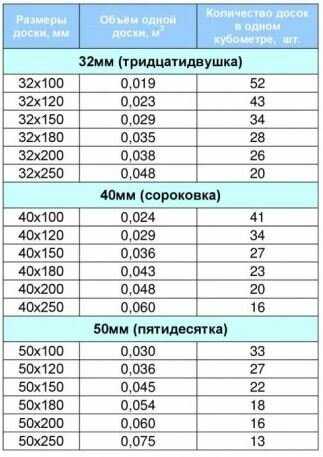

Компания доставляет товары по Москве и Московской области собственным грузовым транспортом, по Санкт-Петербургу и другим регионам России – проверенными транспортными службами.

Чтобы заказать продукцию и узнать стоимость, звоните по тел. +7 (495) 248-20-52 или пишите на [email protected].

Онлайн калькулятор расчета объема пиломатериалов

Поиск для:

Пиломатериалы — продукция из древесины установленных размеров и качества, имеющая, как минимум, две плоско-параллельные пласти.

Пиломатериалы получают в результате продольного деления круглых лесоматериалов (брёвен), а также продольного и поперечного деления полученных частей.

Виды пиломатериалов

В зависимости от ориентации в бревне:

Пиломатериал радиальной распиловки — пиломатериал, полученный ориентированной распиловкой круглых лесоматериалов или брусьев с преимущественным направлением пропилов, близкий к радиусам годичных слоев древесины.
Пиломатериал тангентальной распиловки — пиломатериал, полученный ориентированной распиловкой круглых лесоматериалов с преимущественным направлением пропилов по касательной к годичным слоям древесины.

В зависимости от опилености кромок, обработки строганием и калибрования:

Обрезной пиломатериал — пиломатериал с кромками, опиленными перпендикулярно пластям и с обзолом не более допустимого по соответствующей нормативно-технической документации (обрезной пиломатериал может быть с параллельными и непараллельными (по сбегу) кромками).
Односторонне-обрезной пиломатериал — пиломатериал с одной кромкой, опиленной перпендикулярно пластям, и с обзолом на этой кромке не более допустимого в обрезном пиломатериале.
Необрезной пиломатериал — пиломатериал с неопиленными или частично опиленными кромками, с обзолом более допустимого в обрезном пиломатериале.
Строганый пиломатериал — пиломатериал, у которого обработаны строганием хотя бы одна пласть или обе кромки.
Калиброванный пиломатериал — пиломатериал, высушенный и обработанный до заданного размера.
В зависимости от гарантированности прочностных показателей:
Конструкционные пиломатериалы — пиломатериалы с гарантированными показателями прочности для изготовления деталей несущих конструкций.

В зависимости от вида сортировки:

Пиломатериалы машинной сортировки — конструкционные пиломатериалы, рассортированные с помощью механического устройства, действие которого основано на зависимости между модулем упругости и пределом прочности при изгибе, растяжении, сжатии.
Пиломатериалы визуальной сортировки — пиломатериалы, рассортированные путем внешнего осмотра, основанного на учете размеров, количества, характера и местоположения пороков древесины.

В зависимости от обработки торцов:

Торцованные — пиломатериалы обрезаные в размер по длине.
Неторцованные — пиломатериалы не обрезаные в размер по длине.

По сортименту:

Брус
Брусок
Доска
Шпалы
Обапол
Горбыль

людей нашли эту статью полезной. А Вы?

распределение точек на сфере и соответствующие кубатурные формулы | Журнал численного анализа IMA

Фильтр поиска панели навигации IMA Journal of Numerical AnalysisЭтот выпускIMA JournalsNumerical AnalysisBooksJournalsOxford Academic Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации IMA Journal of Numerical AnalysisЭтот выпускIMA JournalsNumerical AnalysisBooksJournalsOxford Academic Введите поисковый запрос

Расширенный поиск

Журнальная статья

Получить доступ

Дж Флиге,

Джей Флидж

Ищите другие работы этого автора на:

Оксфордский академический

Google Scholar

У Майер

Ищите другие работы этого автора на:

Оксфордский академический

Google Scholar

Журнал численного анализа IMA , том 19, выпуск 2, апрель 1999 г. , страницы 317–334, https://doi.org/10.1093/imanum/19.2.317

Опубликовано:

01 апреля 1999 г.

Цитировать

Cite

J Fliege, U Maier, Распределение точек на сфере и соответствующие кубатурные формулы, Журнал численного анализа IMA , Том 19, Выпуск 2, 19 апреля99, страницы 317–334, https://doi. org/10.1093/imanum/19.2.317

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Разрешения

Закрыть

Advanced Search

Abstract

В приложениях, например, в оптике и астрофизике, требуются высокоточные формулы интегрирования функций на сфере.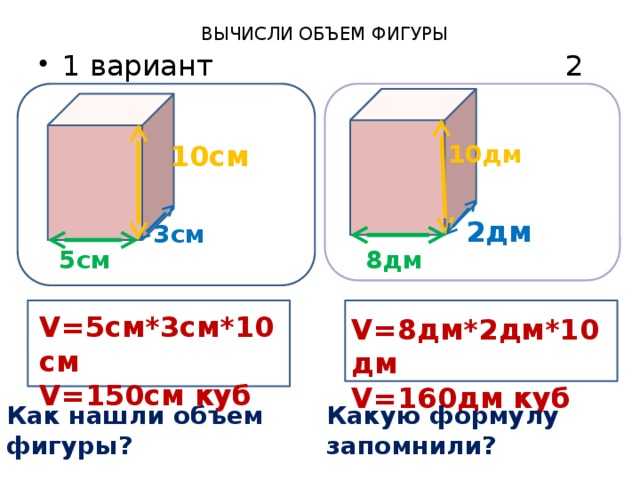 Для построения лучших формул, чем использовались ранее, требуются почти равноудаленные узлы на сфере и веса, принадлежащие этим узлам. Эта проблема тесно связана с задачей оптимальной дисперсии на сфере, а также с теориями сферических планов и многомерными квадратурными формулами Гаусса.

Мы предлагаем двухэтапный алгоритм для вычисления оптимальных положений точек на единичной сфере и соответствующий алгоритм для вычисления соответствующих весов кубатурных формул. Очки, а также веса вычисляются с высокой точностью. Эти алгоритмы могут быть распространены на другие задачи интеграции. Численные примеры показывают, что построенные формулы дают впечатляюще малые ошибки интегрирования до 10 ^-12 .

Этот контент доступен только в формате PDF.

Раздел выпуска:

Артикул

В настоящее время у вас нет доступа к этой статье.

Скачать все слайды

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок.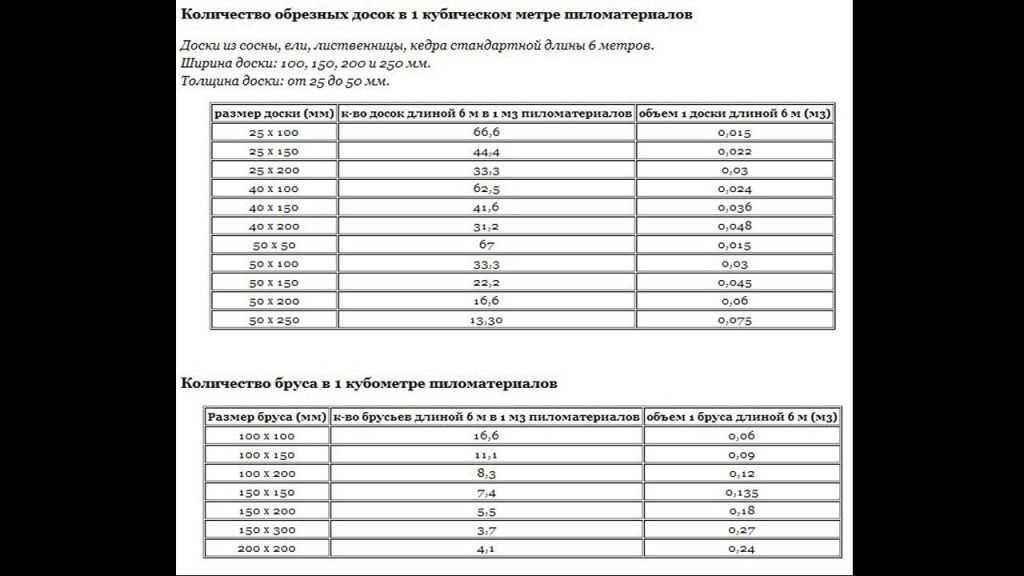 Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

Нажмите Войти через свое учреждение.
Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

Щелкните Войти через сайт сообщества.
Находясь на сайте общества, используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

Просмотр вашей личной учетной записи, в которой выполнен вход, и доступ к функциям управления учетной записью.
Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Стоимость подписки и заказ этого журнала

Варианты покупки книг и журналов в Oxford Academic

Кратковременный доступ

Чтобы приобрести краткосрочный доступ, пожалуйста, войдите в свой личный аккаунт выше.

У вас еще нет личного кабинета? регистр

Распределение точек на сфере и соответствующие кубатурные формулы — Доступ 24 часа

ЕВРО €36,00

32 фунта стерлингов

39 долларов США.

Цитаты

Альтметрика

Дополнительная информация о метриках

Оповещения по электронной почте

Оповещение об активности статьи

Предварительные уведомления о статьях

Оповещение о новой проблеме

Получайте эксклюзивные предложения и обновления от Oxford Academic

Ссылки на статьи по телефону

Последний
Самые читаемые
Самые цитируемые

Новый низкорегулярный интегратор второго порядка для кубического нелинейного уравнения Шредингера

Анализ устойчивости и сходимости численных схем высокого порядка с поглощающими граничными условиями типа DtN для нелокальных волновых уравнений

Случайные точки оптимальны для аппроксимации функций Соболева

О скорости сходимости численной схемы для дробных законов сохранения с шумом

Многократный анализ стохастических гиперболических законов сохранения

Кубатурный фильтр Калмана при минимальной энтропии ошибки с опорными точками для интеграции INS/GPS

[1]	Б. Паркинсон, Дж. Спилкер, П. Аксельрад и П. Энге, Глобальная система позиционирования: теория и приложения . Норвуд, Массачусетс, США: Artech House, 2008.
[2]	Л. Чанг, Дж. Ли и К. Ли, «Выравнивание на основе оптимизации бесплатформенной инерциальной навигационной системы: сравнение и расширение», IEEE Trans. Аэросп. Электрон. Сист. , том. 52, нет. 4, стр. 1697–1713, август 2016 г. doi: 10.1109/TAES.2016.130824
[3]	Д. Титтертон и Дж. Уэстон, Бесплатформенная инерциальная навигационная техника . Лондон, Великобритания: Инженерно-технологический институт, 2004 г. .
[4]	PD Groves, Принципы интегрированных GNSS, инерциальных и мультисенсорных навигационных систем . Вашингтон, США: Американский институт аэронавтики и астронавтики, 1996. .
[5]	М. Гревал, Л. Вейл и А. Эндрюс, Системы глобального позиционирования, инерциальная навигация и интеграция . Хобокен, Нью-Джерси: John Wiley & Sons, 2007. .
[6]	Ф. Чжао, К. Чен, В. Хе и С. Сэм Ге, «Подход к фильтрации на основе MMAE для интегрированной навигационной системы БИНС/ЦНС», IEEE/CAA Journal of Automatica Sinica , vol. 5, нет. 6, стр. 1113–1120, ноябрь 2018 г. doi: 10.1109/JAS.2017.7510445
[7]	Y. Huang, Y. Zhang и L. Chan, «Новый быстрый метод грубой настройки в движении для недорогих SINS с помощью GPS», IEEE/ASME Trans. Мехатроника , вып. 23, нет. 3, pp. 1303–1313, May 2018. doi: 10.1109/TMECH.2018.2835486
[8]	К. Б. Медейрос и М. М. Вандерли, «Многомодельный линейный фильтр Калмана для непредсказуемых сигналов», IEEE Sensors J. , vol. 14, нет. 4, стр. 979–991, апрель 2014 г. doi: 10.1109/JSEN.2013.2291683
[9]	А. Сингх, «Основное развитие гауссовой фильтрации после использования фильтра Калмана без запаха», IEEE/CAA Journal of Automatica Sinica , vol. 7, нет. 5, стр. 1308–1325, сентябрь 2020 г.
[10]	С. Джулиер и Дж. Ульманн, «Новое расширение фильтра Калмана для нелинейных систем», в Проц. 11-й междунар. Симп. Аэрокосмическая/оборонная служба, Simul. Controls , 1997, стр. 182–193.
[11]	К. Х. Ким, Дж. Г. Ли и К. Г. Парк, «Адаптивный двухэтапный расширенный фильтр Калмана для отказоустойчивой слабосвязанной системы INS/GPS», IEEE Trans. Аэросп. Электрон. Сист. , том. 45, нет. 1, стр. 125–137, январь 2009 г. doi: 10.1109/TAES.2009.4805268
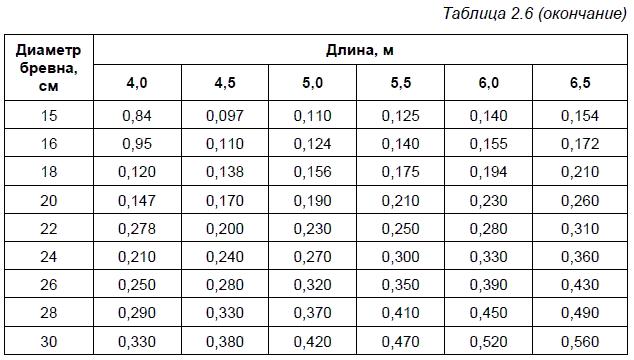[12]	Д. Сан, М. Г. Петовелло и М. Э. Кэннон, «Сверхплотная интеграция GPS/уменьшенный IMU для навигации наземных транспортных средств», IEEE Trans. Аэросп. Электрон. Сист. , том. 49, нет. 3, стр. 1781–1791, июль 2013 г. doi: 10.1109/TAES.2013.6558019
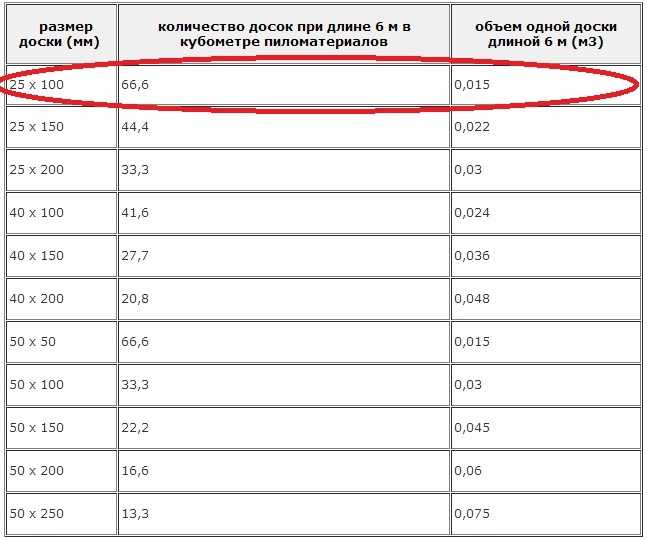[13]	Дж. Вендел, Дж. Мецгер, Р. Моэникес, А. Майер и Г. Ф. Троммер, «Сравнение производительности тесно связанных систем навигации GPS/ИНС на основе расширенных и сигма-точечных фильтров Калмана», Навигация , том. 53, нет. 1, стр. 21–31, август 2014 г.
[14]	J. Zhou, Y. Yang, J. Zhang, E. Edwan и O. Loffeld, «Сильная связь INS/GPS с использованием фильтра Калмана без запаха на основе кватернионов», в Proc. AIAA Guid., Navigat., Control Conf. , Портленд, штат Орегон, США, 2011 г., стр. 1–14.
[15]	Л. Чанг, К. Ли и Б. Ху, «Надежный фильтр M на основе оценки неопределенности процесса Huber для интегрированной INS/GPS», IEEE Sensors J. , vol. 15, нет. 6, стр. 3367–3374, июнь 2015 г. doi: 10.1109/JSEN.2014.2384492
[16]	И. Арасаратнам и С. Хайкин, «Кубатурные фильтры Калмана», IEEE Trans. автомат. Контроль , том. 54, стр. 1254–1269, июнь 2009 г. doi: 10.1109/TAC.2009.2019800
[17]	B. Cui, X. Chen и X. Tang, «Улучшенный кубатурный фильтр Калмана для GNSS/INS на основе преобразования апостериорной ошибки сигма-точек», IEEE Trans. Сигнальный процесс. , том. 65, нет. 11, стр. 2975–2987, март 2017 г. doi: 10.1109/TSP.2017.2679685
[18]	Ю. Чжао, «Оценка эффективности кубатурного фильтра Калмана в тесно связанной навигационной системе GPS/IMU», Сигнальный процесс. , том. 119, стр. 67–79, февраль 2016 г. doi: 10.1016/j.sigpro.2015.07.014
[19]	B. Cui, X. Chen, Y. Xu, H. Huang и X. Liu, «Анализ производительности улучшенного повторяющегося кубатурного фильтра Калмана и его применение к GNSS/INS», ISA Trans. , том. 66, стр. 460–468, январь 2017 г. doi: 10.1016/j.isatra.2016.09.010
[20]	М. Д. Фам, К. С. Лоу, С. Т. Гох и С. С. Чен, «Расширенный фильтр Калмана с планированием усиления для системы определения ориентации наноспутников», IEEE Trans. Аэросп. Электрон. Сист. , том. 51, нет. 2015. Т. 2. С. 1017–1028. doi: 10.1109/TAES.2014.130204
[21]	С. В. Бордонаро, П. В., Ю. Бар-Шалом и Т. Лугинбул, «Сигма-точечный фильтр Калмана с преобразованными измерениями для бистатического гидролокатора и радиолокационного слежения», IEEE Trans. Аэросп. Электрон. Сист. , том. 55, нет. 1, стр. 147–159, февраль 2019 г. doi: 10.1109/TAES.2018.2849179
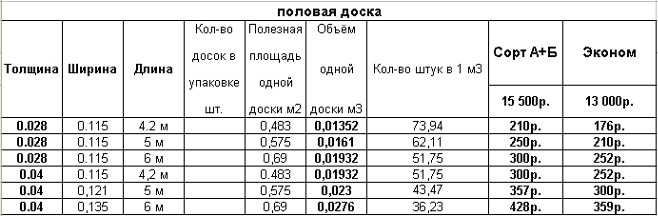[22]	K. Feng, J. Li, X. Zhang, X. Zhang, C. Shen, H. Cao, Y. Yang и J. Liu, «Улучшенный кубатурный фильтр Калмана с сильным отслеживанием для интегрированных навигационных систем GPS/INS, Датчики , об. 18, нет. 6, статья № 1919, июнь 2018 г. doi: 10.3390/s18061919
[23]	X. Chen, C. Shen, WB Zhang, M. Tomizuka, Y. Xu и KL Chiu, «Новый гибрид сильного фильтра Калмана и вейвлетной нейронной сети для GPS/INS во время сбоев GPS», Measurement , vol. 46, нет. 10, стр. 3847–3854, декабрь 2013 г. doi: 10.1016/j.measurement.2013.07.016
[24]	Арулампалам М. С., Маскелл С., Гордон Н. и Клапп Т., «Учебное пособие по фильтрам частиц для онлайн-нелинейного/негауссовского байесовского отслеживания», IEEE Trans. Сигнальный процесс. , том. 50, нет. 2, стр. 174–188, февраль 2002 г. doi: 10.1109/78.978374
[25]	X. Liu, H. Qu, J. Zhao и P. Yue, «Кубатурный фильтр Калмана с квадратным корнем максимальной коррентропии с применением к интегрированным системам SINS/GPS», ISA Trans. , том. 80, стр. 195–202, май 2018 г. doi: 10.1016/j.isatra.2018.05.001
[26]	JC Príncipe, Информационно-теоретическое обучение: энтропия Реньи и перспективы ядра , Нью-Йорк, штат Нью-Йорк, США: Springer, 2010.
[27]	Д. Л. Алспах и Х. Соренсон, «Нелинейная байесовская оценка с использованием приближений суммы Гаусса», IEEE Trans. автомат. Контроль , том. 17, нет. 4, стр. 439–448, август 1972 г. doi: 10.1109/TAC.1972.1100034
[28]	Y. Huang и Y. Zhang, «Новый устойчивый к неопределенности процесса фильтр Калмана на основе t Стьюдента для интеграции SINS/GPS», IEEE Access , vol. 5, стр. 14391–14404, июль 2017 г. doi: 10.1109/ACCESS.2017.2726519
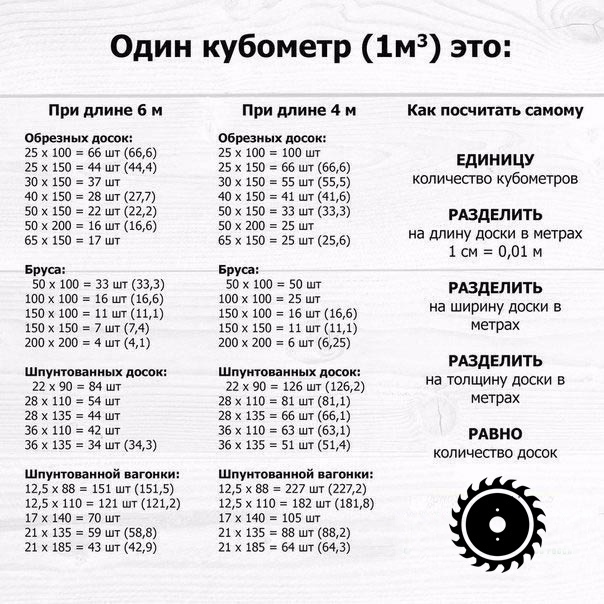[29]	О. Страка и Й. Дуник, «Стохастическая интеграция Студенческая − t filter», в Proc. 20-й междунар. конф. Инф. Fusion , стр. 1–8, июль 2017 г.
[30]	Ю. Хуанг и Ю. Чжан, «Надежный стохастический кубатурный фильтр Стьюдента на основе t для нелинейных систем с шумами процессов и измерений с тяжелыми хвостами», IEEE Access , vol. 5, нет. 5, стр. 7964–7974, май 2017 г.
[31]	F. Sun и L. Tang, «Кубатурный фильтр частиц», Syst. англ. Электрон. , том. 33, нет. 11, стр. 2554–2557, ноябрь 2011 г.
[32]	B. Cui, X. Chen, X. Tang, H. Huang и X. Liu, «Надежный кубатурный фильтр Калмана для GNSS/INS с отсутствующими наблюдениями и цветным шумом измерений», ISA Trans. , том. 72, стр. 138–146, январь 2018 г. doi: 10.1016/j.isatra.2017.09.019
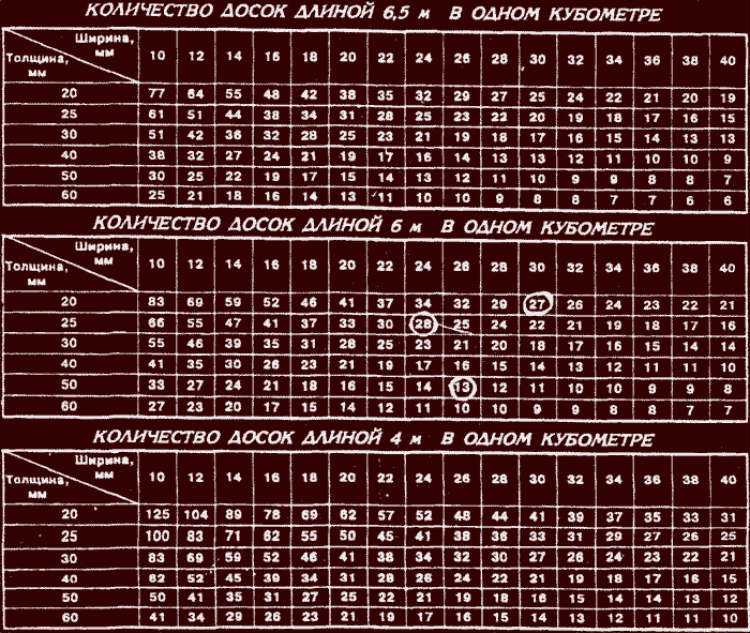[33]	Мили Л., Стино Г., Добрака Ф. и Френч Д. Надежный метод оценки для выявления топологических ошибок // IEEE Trans. Система питания , том. 14, нет. 4, стр. 1469–1476, ноябрь 1999 г. doi: 10.1109/59.801932
[34]	Л. Мили и К. В. Коукли, «Надежная оценка в структурированной линейной регрессии», Энн. Статист. , том. 24, нет. 6, стр. 2593–2607, декабрь 1996 г.
[35]	Ю. С. Шмалий, «Итеративный алгоритм типа Калмана, игнорирующий шум и начальные условия», IEEE Trans. Сигнальный процесс. , том. 59, нет. 6, стр. 2465–2473, июнь 2011 г. doi: 10.1109/TSP.2011.2129516
[36]	Т. Чиен-Хао, С. Ф. Лин и Дж. Дах-Цзин, «Надежный кубатурный фильтр Калмана на основе Губера для обработки GPS-навигации», J. Navigat , vol. 229, нет. 7, том. 70, стр. 527–546, Otc. 2016.
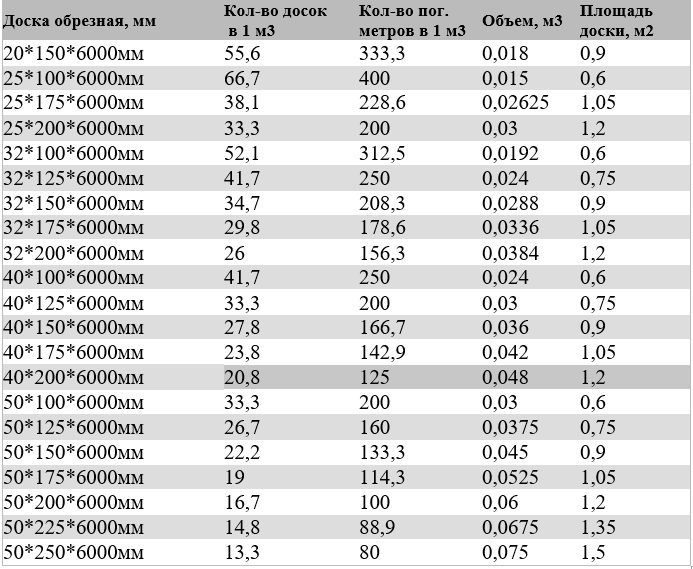[37]	К. Ли, Б. Ху, Л. Чанг и Ю. Ли, «Надежный квадрат — кубатурный корневой фильтр Калмана на основе методологии оценки Хубера», Proc. Инст. мех. англ. Г-Дж. воздух , том. 229, нет. 7, стр. 1236–1245, июнь 2015 г. doi: 10.1177/0954410014548698
[38]	А. Сингх и Дж. К. Принсипе, «Использование коррентропии как функции стоимости в линейных адаптивных фильтрах», в Proc. Междунар. Совместная конф. Нейронная сеть (IJCNN) , июль 2009 г., стр. 2950–2955.
[39]	Б. Чен, Дж. Ван, Х. Чжао, Н. Чжэн и Дж. К. Принсипи, «Сходимость алгоритма с фиксированной точкой по критерию максимальной коррентропии», IEEE Signal Process. лат. , том. 22, нет. 10, стр. 1723–1727, Otc. 2015. doi: 10.1109/LSP.2015.2428713
[40]	B. Chen, X. Liu, H. Zhao, JC Príncipe, «Максимальный корретропный фильтр Калмана», Automatica , vol. 76, стр. 70–77, февраль 2017 г. doi: 10.1016/j.automatica.2016.10.004
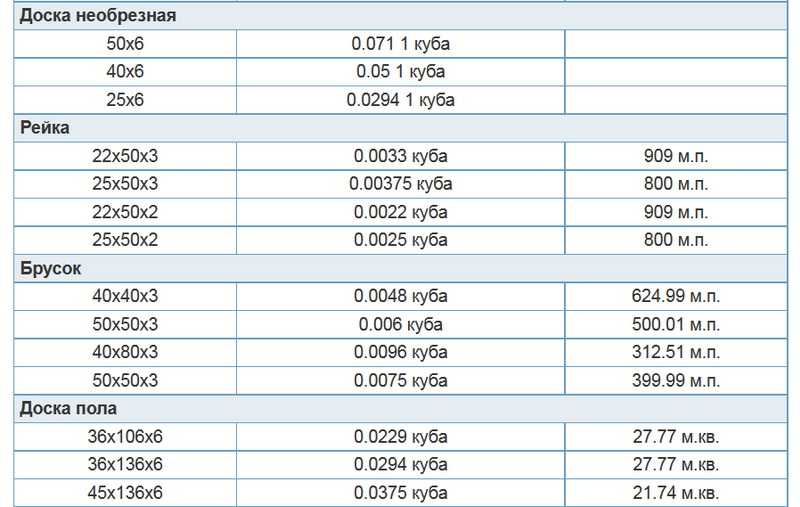[41]	H. Wang, H. Li, J. Zuo, W. Zhang, and H. Wang, «Надежный фильтр Калмана без производной максимальной коррентропии и сглаживатель», Доступ IEEE , том. 6, стр. 70794–70807, ноябрь 2018 г. doi: 10.1109/ACCESS.2018.2880618
[42]	С. Ван, С. Инь, Г. Цянь, Ю. Фенг, С. Кай и Л. Ван, «Кубатурный фильтр Калмана с максимальной корретропией, основанный на статистической линейной регрессии», C.N. Патент, 106487358 A, 8 марта 2017 г. [Онлайн]. Доступно: https://ieeexplore.ieee.org/document/9546666.
[43]	Б. Чен, Л. Син, Б. Сюй, Х. Чжао и Дж. К. Принсипи, «Понимание надежности оценки энтропии с минимальной ошибкой», IEEE Trans. Нейронная сеть. Учиться. Сист. , том. 29, нет. 3, стр. 731–737, март 2018 г. doi: 10.1109/TNNLS.2016.2636160
[44]	Д. Эрдогмус и Дж. К. Принсипе., «Минимизация энтропии ошибки для контролируемого обучения нелинейных адаптивных систем», IEEE Trans. Сигнальный процесс. , том. 50, нет. 7, стр. 1780–1786, июль 2002 г. doi: 10.1109/TSP.2002.1011217
[45]	Y. Zhang, B. Chen, X. Liu, Z. Yuan, JC Príncipe, «Сходимость алгоритма энтропии минимальной ошибки с фиксированной точкой», Entropy , vol. 17, нет. 8, стр. 5549–5560, август 2015 г.
[46]	Чен Б., Данг Л., Гу Ю., Чжэн Н. и Принцип Дж. К., «Энтропийный фильтр Калмана с минимальной ошибкой», IEEE Trans. Сист. , Человек , Кибер. , Сист. , том. 51, нет. 9, стр. 5819–5829, сентябрь 2021 г.
[47]	Лю В., Покхарел П. П. и Принсипе Дж. К., «Энтропия ошибок, коррентропия и М-оценка», в Proc. 16-й семинар IEEE по машинному обучению. Сигнальный процесс ., 2006, стр. 179–184.
[48]	Дж. Чжао и Л. Мили, «Надежный фильтр Калмана с обобщенным максимальным правдоподобием для оценки динамического состояния энергосистемы», IEEE J. Sel. Темы Сигнальный процесс. , том. 12, нет. 4, стр. 578–592, август 2018 г. doi: 10.1109/JSTSP.2018.2827261
[49]	К. Андреу и В. Каратанасси, «Оценка количества конечных элементов с использованием надежного метода обнаружения выбросов», IEEE J. Сел. Темы Наблюдение за Землей. Дистанционный датчик , том. 7, нет. 1, стр. 247–256, январь 2014 г. doi: 10.1109/JSTARS.2013.2260135
[50]	B. Chen, X. Wang, Y. Li, and JC Príncipe, «Критерий максимальной корретропии с переменным центром», IEEE Signal Process. лат. , том. 26, нет. 8, стр. 1212–1216, август 2019 г. doi: 10.1109/LSP.2019.2925692
[51]	Б. Чен, С. Ван, З. Юань, П. Рен и Дж. Цинь, «Многоядерная корретропия для надежного обучения», [онлайн]. Доступно: https://ieeexplore.ieee.org/document/9546666. Дата обращения: 15 октября 2021 г.
[52]	Б. No related posts. Категория: Разное Навигация по записям Ои мкд: Содержание общего имущества многоквартирного дома Мангал с двойным дном: жаровня с колосником своими руками Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт © 2019 Ассоциация ЖКХ «Развитие» и Компания «ЖКХ Девелопмент». При использовании материалов ссылка на первоисточник обязательна. 2024 © Все права защищены.