Онлайн-калькулятор расчета досок, расчет кубов, количества, стоимости
Оставить комментарий
Содержание
- Расчет кубатуры
- Расчет количества
- Расчет стоимости
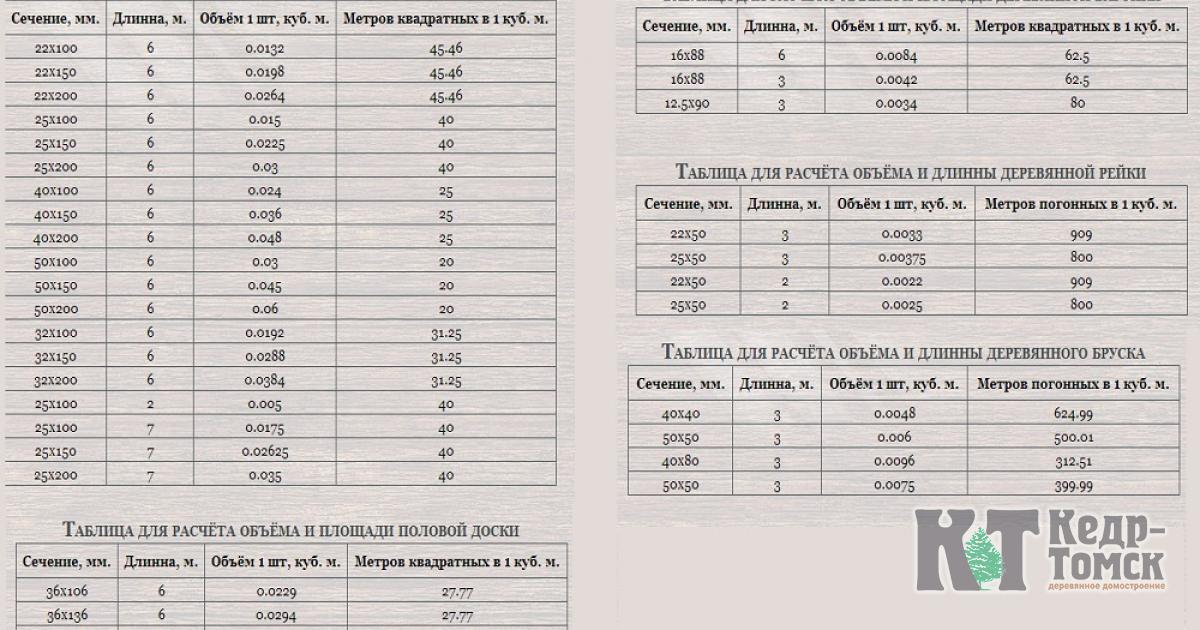
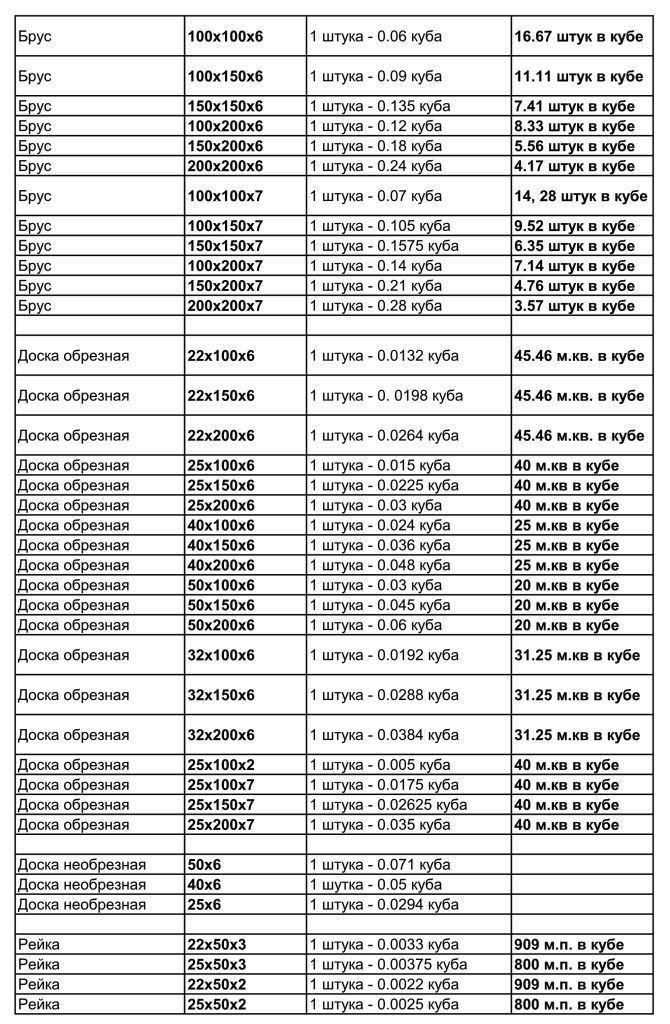
Бесплатный онлайн-калькулятор позволит Вам быстро и просто рассчитать количество, кубатуру и стоимость досок, поможет предварительно оценить предстоящий уровень расходов на строительство. Удобный калькулятор не требует специальных навыков и знаний. Вы сможете легко провести предварительную калькуляцию после ввода простых исходных данных.
Доска относится к основным видам пиломатериалов, широко применяемых в домостроении, при возведении подсобных и хозяйственных построек. Поставки традиционно рассчитываются в кубических метрах. В кубах калькулируются и цены. Поэтому при проектировании строительства важно точно просчитать объем пиломатериала.
Для быстрой калькуляции вам потребуется минимум исходных данных. В соответствующие поля необходимо ввести следующие основные параметры:
- габариты применяемого в строительстве пиломатериала – длину, ширину, толщину;
- число используемого древесного материала в штуках;
- цену за кубический метр.
После ввода данных программа моментально проведет расчет кубов доски. В итоге вы получите такие результаты, как объем одной единицы, так и всей партии. Также программа посчитает, стоимость за штуку и за указанное количество.
При планировании закупки материала для строительства часто возникает необходимость определить его численность в определенном объеме. Например, это нужно для того, чтобы узнать, сколько кубов вам потребуется заказать, если известно сколько штук требуется для выполнения определенных отделочных или строительных работ.
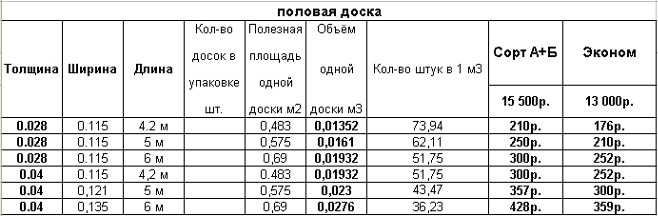Для проведения калькуляции необходимо ввести следующие исходные данные:- размеры единицы пиломатериала – длина, ширина, толщина;
- кубатура;
- цену материала за 1 кубический метр.
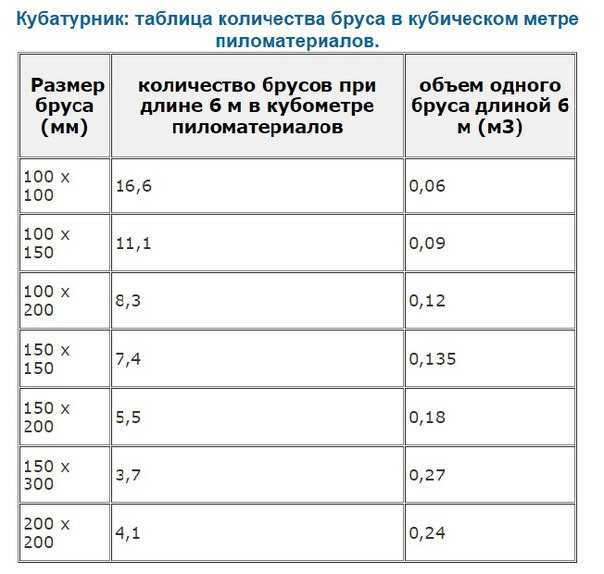
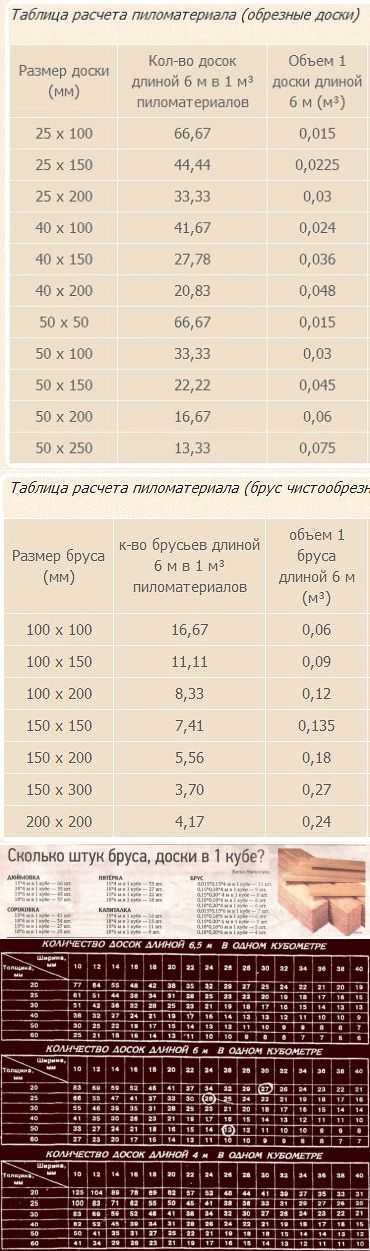
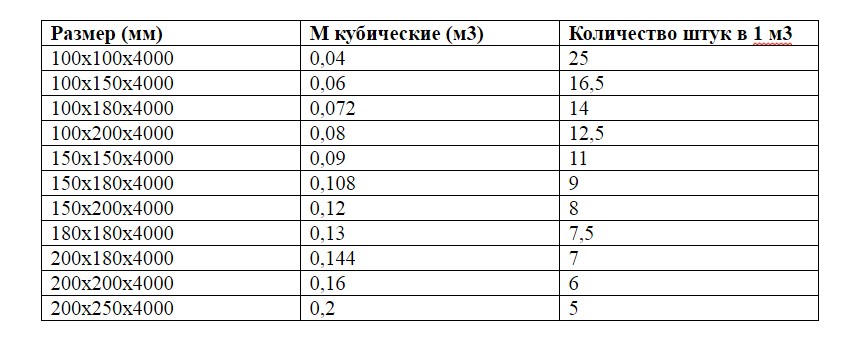
После этого достаточно нажать кнопку «Рассчитать», и Вы сразу же получите требуемые значения. В том числе с помощью приложения можно узнать, сколько единиц заданного размера как в одном кубическом метре, так и в указанном.
Любого застройщика всегда интересует уровень расходов на стройматериалы. При ведении деревянного строительства значительные затраты приходятся именно на пиломатериалы. С нашим калькулятором вы сможете легко определить необходимые затраты. Расчет стоимости доски предусмотрен при калькуляции как кубатуры, так и количества материала. В том числе можно узнать цену одной единицы, за указанную численность или за указанные исходные кубометры.
РубрикаРасчет пиломатериалов
Калькулятор расчета объема груза — Avrora Logistic
- На главную
- Расписание
движения - КАЛЬКУЛЯТОР
ТАМОЖЕННЫХ
ПЛАТЕЖЕЙ - КАЛЬКУЛЯТОР
СБОРНЫХ
ГРУЗОВ - КАЛЬКУЛЯТОР
ЦЕЛЫХ
КОНТЕЙНЕРОВ - РАСЧЕТ ОБЪЕМА
ГРУЗА
Рассчитайте объем вашего груза
РАСЧЕТ ОБЪЕМА ГРУЗА
ШИРИНА (W) *
ДИАМЕТР (D) *
РАСЧЕТ ОБЪЕМА КоробкиЦилиндр
ВЫСОТА (H) * ЕДИНИЦА ИЗМЕРЕНИЯ * ммсмм
ДЛИНА (L) *
КОЛИЧЕСТВО КОРОБОК *
КОЛИЧЕСТВО ЦИЛИНДРОВ *
ИТОГО:
Объем одной коробки Объем одного цилиндра | 0 м³ |
| Общий объем | 0 м³ |
ИСПОЛЬЗУЙТЕ ПОЛУЧЕННЫЕ РАСЧЕТЫ
ДЛЯ ОФОРМЛЕНИЯ ЗАЯВКИ
Далее
- На главную
-
Расписание
движения -
РАСЧЕТ ОБЪЕМА
ГРУЗА -
КАЛЬКУЛЯТОР
ТАМОЖЕННЫХ
ПЛАТЕЖЕЙ -
КАЛЬКУЛЯТОР
СБОРНЫХ
ГРУЗОВ -
КАЛЬКУЛЯТОР
ЦЕЛЫХ
КОНТЕЙНЕРОВ
Возникли вопросы?
Я согласен на обработку персональных данных в порядке и на условиях, указанных по ссылке
Прикрепить файл (максимальный размер 20 Мб)
Калькулятор размера и веса (прямоугольная коробка)
Создано Mateusz Mucha
Отзыв от Jack Bowater
Последнее обновление: 30 января 2023 г.
позволяет определить, сколько весит прямоугольная коробка (например, кирпич, книга, дверь, куб-компаньон и т. д.) на основе размера и плотности . Он также может найти плотность объекта, если вы знаете его объем и вес. Например, если у вас есть кирпич размером 92 × 57 × 203 мм и плотностью 2,4 кг/л, вы обнаружите, что вес этого объекта составляет 2,555 кг.
Наш калькулятор объема и калькулятор плотности решают проблемы, связанные с этим. Калькулятор бетона позволяет рассчитать, сколько мешков бетона вам нужно, а калькулятор кирпича отвечает на вопрос: сколько мне нужно кирпичей?.
Как определить вес коробки без весов?
Чтобы найти вес коробки без весов, вы можете использовать соотношение между массой и объемом: масса = плотность × объем .
Начните с измерения размеров коробки.
Найдите объем коробки
Оцените или найдите плотность интересующего материала.
Убедитесь, что единицы соответствуют (например, используйте кубические метры для объема и килограммы на кубический метр для плотности), и рассчитайте массу, используя:
масса = плотность × объем.
Сколько весит железный куб со стороной 40 см?
Куб весит примерно 504 кг . Чтобы найти этот результат:
Вычислить объем куба:
V = l × l × l = 0,4 × 0,4 × 0,4 = 0,064 м³
Определить плотность железа: d = 7874 кг/м³ .
Найдите массу, используя:
масса = плотность × объем = 7874 кг/м³ × 0,064 м³ = 503,94 кг
Куб со стороной 40 см из железа весит более полтонны!
Как преобразовать объем в вес?
Чтобы преобразовать объем в вес, вам необходимо знать плотность материала , с которым вы работаете.
Плотность — это мера массы известного объема: чем выше плотность, тем выше вес объекта фиксированного размера. Вы можете найти плотность многих материалов в Интернете или измерить ее самостоятельно по образцу.
Вес пропорционален размеру?
Да , вес и размер пропорциональны — по крайней мере, если учесть один и тот же материал. Константа пропорциональности известна как плотность , свойство материи, характеризующее вес данного объема.
Матеуш Муха
Размер
Длина
Высота
Объем
Вес
Плотность
Вес
Оформить заказ 6 похожих конструкций0003
Борт-футКубический ярдГаллонов на квадратный фут… Еще 3
Калькулятор вероятности игры в кости
Создано Wojciech Sas, PhD
Отзыв от Bogna Szyk и Jack Bowater кости
Калькулятор вероятности игры в кости — отличный инструмент, если вы хотите оценить вероятность броска кубиков по множеству вариантов .
В набор входит множество различных многогранных кубиков, так что вы можете исследовать вероятность выпадения 20-гранного кубика и обычного кубического кубика.
Итак, просто оценивайте шансы и играйте! Вы также найдете краткие описания каждой опции в тексте.
🔎 У тебя нет физических кубиков? Нет проблем — попробуйте наш калькулятор игры в кости!
Многогранная кость
Все знают, что такое обычная шестигранная кость, и, скорее всего, многие из вас уже сыграли тысячи игр, где использовалась одна (или более) t Но знаете ли вы, что существует разные типы штампов ? Из бесчисленных возможностей самые популярные игральные кости включены в набор игральных костей Dungeons & Dragons , который содержит семь различных многогранных игральных костей: равносторонний треугольник;
💡 Вы можете отточить свою стратегию D&D, используя калькулятор покупки очков Omni 5e.
Не волнуйтесь, мы учитываем каждый из этих кубиков в нашем калькуляторе вероятности. Вы можете выбрать то, что вам нравится, и, например, притвориться, что бросаете сразу пять 20-гранных кубиков!
Как рассчитать вероятность броска костей?
Что ж, вопрос сложнее, чем кажется на первый взгляд, но вскоре вы убедитесь, что ответ не так уж и страшен! Все дело в математике и статистике.
Прежде чем приступать к каким-либо вычислениям, давайте определим некоторые переменные, которые мы будем использовать в формулах. n – количество игральных костей, s – количество отдельных граней кости, p – вероятность выпадения любого значения с кости, а P – общая вероятность решения задачи.
Существует простое соотношение – p = 1/с , поэтому вероятность получить 7 на 10-гранном кубике в два раза больше, чем на 20-гранном кубике.
Вероятность выпадения одного и того же значения на каждом кубике — хотя шанс выпадения определенного значения на одном кубике равен p , нам нужно только умножить эту вероятность на саму себя столько раз, сколько игральных костей. Другими словами, вероятность P равна p в степени n , или P = pⁿ = (1/s)ⁿ . Если мы рассмотрим три 20-гранных кубика, шанс выпадения 15 на каждом из них составляет: P = (1/20)³ = 0,000125 (или P = 1,25·10⁻⁴ в научной записи). И если вы заинтересованы в прокатке набора из любых одинаковых значений, просто умножьте результат на общее количество граней кубика: P = 0,000125 · 20 = 0,0025 .
Вероятность выпадения всех значений, равных или превышающих y – задача аналогична предыдущей, но на этот раз p равно 1/с , умноженным на все возможности, удовлетворяющие начальному условию. Например, допустим, у нас есть обычный кубик и y = 3 . Мы хотим, чтобы прокатанное значение было либо 6 , 5 , 4 , либо 3 . Тогда переменная p равна 4 · 1/6 = 2/3 , а окончательная вероятность равна P = (2/3)ⁿ .
Вероятность выпадения всех значений, равных или меньших y — этот вариант почти такой же, как и предыдущий, но на этот раз нас интересуют только числа, равные или меньшие нашей цели. Если мы возьмем одинаковые условия ( s=6 , y=3 ) и применим их в этом примере, мы увидим, что значения 1 , 2 и 3 удовлетворяют правилам, а вероятность равно: P = (3 · 1/6)ⁿ = (1/2)ⁿ .
Вероятность выпадения ровно X одинаковые значения (равные y ) из набора — представьте, что у вас есть набор из семи 12-гранных игральных костей, и вы хотите узнать шансы получить ровно две девятки . Это как-то отличается от предыдущего, потому что только часть всего набора должна соответствовать условиям . Здесь на помощь приходит биномиальная вероятность. Формула биномиальной вероятности:
P(X=r) = nCr · pʳ · (1-p)ⁿ⁻ʳ ,
где r — количество успехов, а nCr — количество комбинаций (также известное как « n выбрать r »).
В нашем примере мы имеем n = 7 , p = 1/12 , r = 2 , nCr = 21 , поэтому окончательный результат: P(X=2) = 21 · (1 /12)² · (11/12)⁵ = 0,09439 или P(X=2) = 9,439% в процентах.
🙋 Более подробную информацию по этой теме вы можете найти в нашем калькуляторе биномиального распределения.
Вероятность выпадения как минимум X одинаковых значений (равных y ) из набора — задача очень похожа на предыдущую, но на этот раз результатом является сумма вероятностей для X =2,3,4,5,6,7 . Переходя к числам, мы имеем: P = P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X= 7) = 0,11006 = 11,006% . Как и следовало ожидать, результат немного выше. Иногда точная формулировка проблемы увеличивает ваши шансы на успех. 9k&\binom{n}{k}\\ &\binom{r\!-s\!\cdot\!k\!-\!1}{n\!-\!1} \end{split}P(r,n,s)=sn1k=0∑⌊(r−n)/s⌋(−1)k(kn)(n−1r−s⋅k−1 )
Однако мы также можем попробовать решить эту задачу вручную. Один из подходов состоит в том, чтобы найти общее количество возможных сумм. С парой обычных игральных костей мы можем получить 2,3,4,5,6,7,8,9,10,11,12 , но эти результаты не эквивалентны !
Взгляните; есть только один способ получить 2 : 1+1 , но за 4 , есть три разных варианта: 1+3 , 2+2 , 3+1 , а для 12 опять же только один вариант: 6+6 .
Оказывается, 7 является наиболее вероятным результатом с шестью вариантами: 1+6 , 2+5 , 3+4 , 4+3 , 5+2 и 6+ 1 . Количество перестановок с повторениями в этом наборе равно 36 . Наш калькулятор перестановок может быть полезен для поиска перестановок для других типов игральных костей. Мы можем оценить вероятности как отношение благоприятных исходов ко всем возможным исходам: P(2) = 1/36 , P(4) = 3/36 = 1/12 , P(12) = 1/36 , P(7) = 6/36 = 1/6 .Чем больше игральных костей, тем ближе функция распределения сумм к нормальному распределению. Как и следовало ожидать, по мере увеличения количества игральных костей и граней все больше времени уходит на оценку результата на листе бумаги. К счастью, это не относится к нашему калькулятору вероятности игры в кости!
Вероятность выпадения суммы из множества, не ниже X — как и в предыдущей задаче, мы должны найти все результаты, которые соответствуют начальному условию, и разделить их на количество всех возможностей.
Учитывая набор из трех десятигранных игральных костей, мы хотим получить сумму не менее 27 . Как мы видим, мы должны сложить все перестановки для 27 , 28 , 29 и 30 , то есть 10, 6, 3 и 1 соответственно. Всего из 1000 возможностей 20 хороших исходов, поэтому конечная вероятность: P(X ≥ 27) = 20/1000 = 0,02 .Вероятность выпадения суммы из множества, не выше X — процедура точно такая же, как и для предыдущей задачи, но мы должны складывать только суммы меньше или равные цели. Имея тот же набор костей, что и выше, какова вероятность того, что выпадет не более 26 ? Если бы вы делали это шаг за шагом, потребовались бы годы, чтобы получить результат (суммировать все 26 сумм). Но, если подумать, мы только что вычислили дополнительное событие в предыдущей задаче. Суммарная вероятность дополнительных событий точно равна 1 , поэтому вероятность здесь равна: P(X ≤ 26) = 1 — 0,02 = 0,98 .
Когда использовать калькулятор вероятности игры в кости?
Существует множество настольных игр, в которых вы по очереди бросаете кубик (или игральные кости), и результаты могут использоваться в различных контекстах. Допустим, вы играете в Dungeons & Dragons и атакуете. Класс брони вашего противника 17 . Вы бросаете 20-гранный кубик, надеясь, что выпадет как минимум 15 с вашим модификатором +2. Этого должно быть достаточно. При этих условиях вероятность успешной атаки равна 0,30 . Если вы знаете шансы на успешную атаку, вы можете выбрать, хотите ли вы атаковать эту цель или выбрать другую с лучшими шансами.
Или, может быть, вы играете в The Settlers of Catan и надеетесь выбросить ровно 8 на двух шестигранных кубиках, так как этот результат принесет вам драгоценные ресурсы. Просто воспользуйтесь нашим калькулятором вероятности в костях, и вы увидите, что вероятность составляет около 0,14 – вам лучше повезти на этом ходу!
Играть или пасовать? — Давай сыграем в игру!
Существуют различные виды игр, например, лотереи, где ваша задача состоит в том, чтобы сделать ставку в зависимости от шансов.
Бросание игральных костей является одним из них. Хотя некоторые риски неизбежны, вы можете выбрать наиболее выгодный вариант и максимизировать свои шансы на победу. Взгляните на этот пример.Представьте, что вы играете в игру, в которой у вас есть один из трех вариантов на выбор , а именно:
- Сумма пяти десятигранных костей не менее 30 ;
- Сумма пяти 12-гранных игральных костей не превышает 28 ;
- Сумма пяти 20-гранных костей не меньше 59 .
Вы выиграете, только если выпадет выбранный вами вариант. Вы также можете отказаться, если чувствуете, что ничего из этого не произойдет. Интуитивно трудно оценить наиболее вероятный успех, но с нашим калькулятором вероятности в костях для оценки всех вероятностей требуется всего лишь мгновение ока.
Полученные значения:
- P₁ = 0,38125 для 10-гранного игрального кубика;
- P₂ = 0,3072 для 12-гранной кости; и
- P₃ = 0,3256 для 20-гранной кости.
Вероятность успешного прохода равна произведению дополнительных событий остальных вариантов:
- P₄ = (1-P₁) · (1-P₂) · (1-P₃) = 0,61875 · 0,6928 · 0,6744 = 0,2891 .
Мы видим, что самый благоприятный вариант — первый, а прохождение — наименее вероятное событие. Мы не можем гарантировать, что вы всегда будете выигрывать, но мы настоятельно рекомендуем вам выбрать для игры 10-гранный набор костей.
Часто задаваемые вопросы
Что такое вероятность?
Вероятность определяет, насколько вероятны определенные события . Простая формула для вероятности: число желаемых исходов/количество возможных исходов . В настольных играх или азартных играх вероятность выпадения костей используется для определения вероятности выпадения определенного числа , например, какова вероятность выпадения определенного числа одним кубиком?
Сколько возможных исходов может быть при бросании двух игральных костей?
Есть 36 исходов при бросании двух игральных костей .
Для одного игрального кубика есть шесть граней, и для любого броска есть шесть возможных исходов . Для две кости , вы должны перемножить количество возможных исходов вместе, чтобы получить 6 × 6 = 36 . При последующих бросаниях просто умножьте результат на 6 . Если вы используете кости другой формы, вместо 6 введите число их граней .Какова вероятность того, что при броске 2 игральных костей выпадет 7?
Это 1/6 или 0,1666667 . Предположим, что всего 7 встречается хотя бы один раз . Для 2 игральных костей существует 6 способов бросить сумму 7 — (1,6), (2,5), (3,4), (4,3), (5,2), (6 ,1) . Общее количество комбинаций для пары кубиков равно 36 . Таким образом, вероятность суммирования до 7 равна 6/36 = 1/6 = 0,1666667 .
Сколько раз я выбрасываю 5 на паре костей?
20 .
Оказывается, 7 является наиболее вероятным результатом с шестью вариантами: 1+6 , 2+5 , 3+4 , 4+3 , 5+2 и 6+ 1 . Количество перестановок с повторениями в этом наборе равно 36 . Наш калькулятор перестановок может быть полезен для поиска перестановок для других типов игральных костей. Мы можем оценить вероятности как отношение благоприятных исходов ко всем возможным исходам: P(2) = 1/36 , P(4) = 3/36 = 1/12 , P(12) = 1/36 , P(7) = 6/36 = 1/6 .
Учитывая набор из трех десятигранных игральных костей, мы хотим получить сумму не менее 27 . Как мы видим, мы должны сложить все перестановки для 27 , 28 , 29 и 30 , то есть 10, 6, 3 и 1 соответственно. Всего из 1000 возможностей 20 хороших исходов, поэтому конечная вероятность: P(X ≥ 27) = 20/1000 = 0,02 .
Бросание игральных костей является одним из них. Хотя некоторые риски неизбежны, вы можете выбрать наиболее выгодный вариант и максимизировать свои шансы на победу. Взгляните на этот пример.
Для одного игрального кубика есть шесть граней, и для любого броска есть шесть возможных исходов . Для две кости , вы должны перемножить количество возможных исходов вместе, чтобы получить 6 × 6 = 36 . При последующих бросаниях просто умножьте результат на 6 . Если вы используете кости другой формы, вместо 6 введите число их граней .