Емкость конденсаторов: определение, формулы, примеры.
Определение 1Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C=qφ1-φ2=qU.
Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
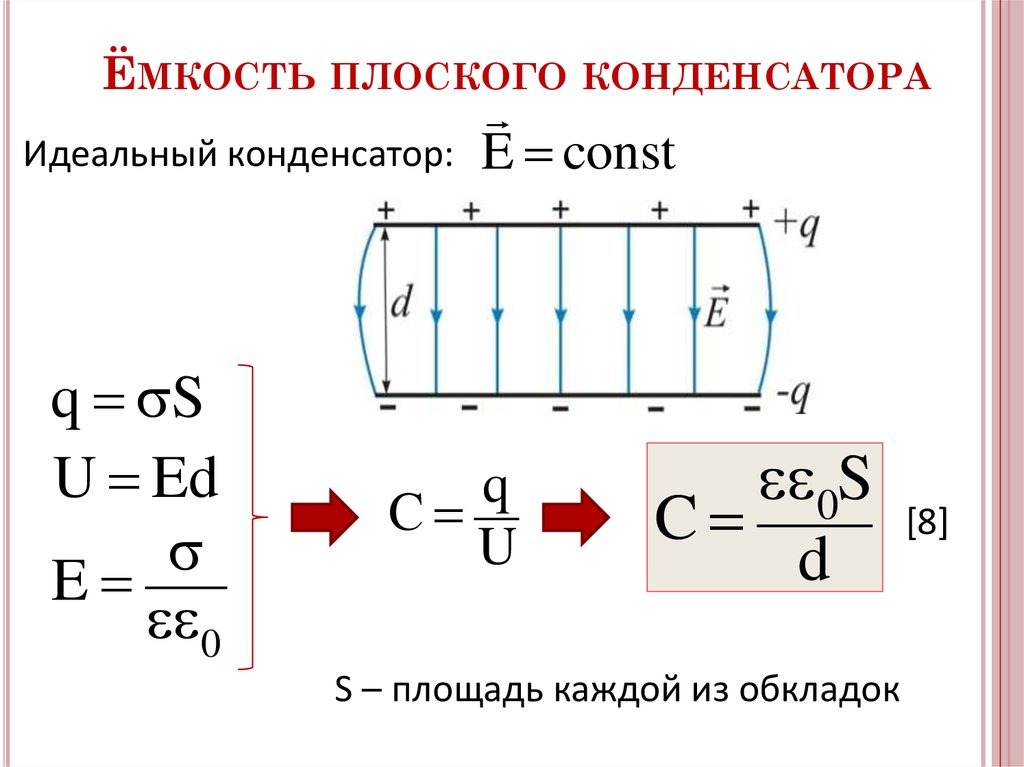
Плоский конденсатор
Определение 2Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.
Формула для расчета электроемкости записывается как
C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε — диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
Рисунок 1
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:
C=ε0Sd1ε1+d2ε2+…+dNεN.
Сферический конденсатор
Определение 3Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2.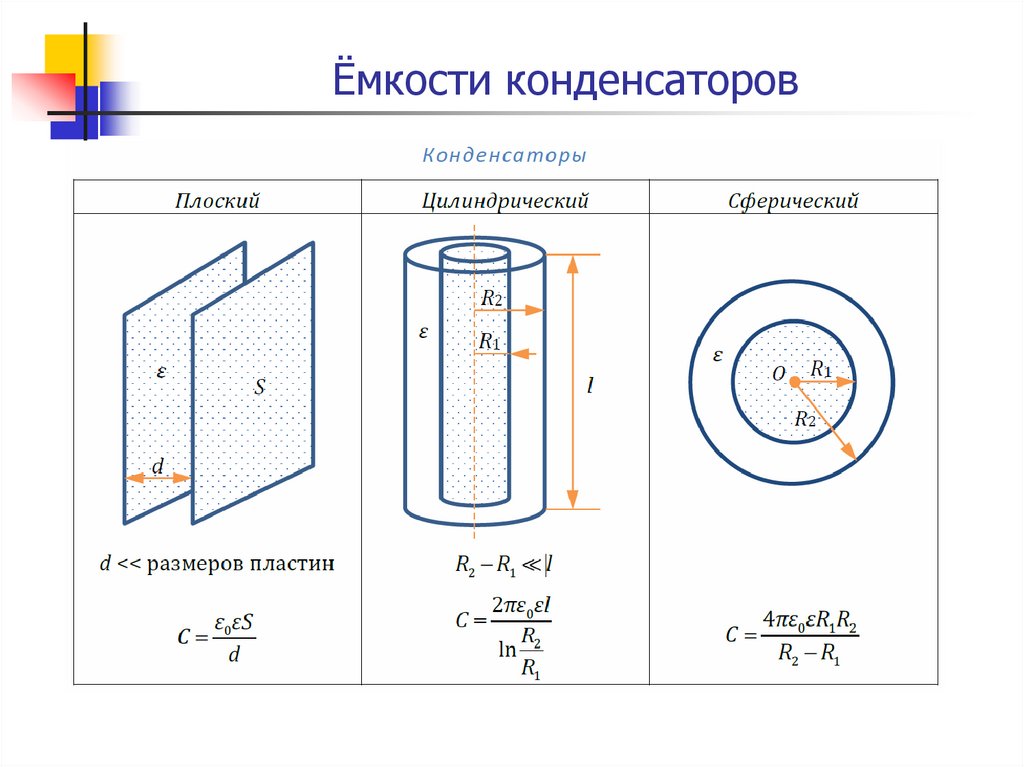 Емкость рассчитывается по формуле:
Емкость рассчитывается по формуле:
C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.
Рисунок 2
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
C=2πεε0llnR2R1, где l — высота цилиндров, R1 и R2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.
Рисунок 3
Определение 4Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.
Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:
C=∑i=1NCi.
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Пример 1Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.
Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
C=εε0Sd.
Значения:
ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.
Подставим числовые выражения и вычислим:
C=8,85·10-12·10-410-3=8,85·10-13 (Ф).
Ответ: C≈0,9 пФ.
Пример 2Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения — 103 В.
Значение напряжения — 103 В.
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x — расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
q=CU.
Для сферического конденсатора предусмотрена формула вида
C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.
Производим подстановку выражений для получения искомой напряженности:
E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.
Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:
E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.
Ответ: E=3,45·104 Вм.
Автор: Роман Адамчук
Преподаватель физики
По какой формуле найти ёмкость (объем) конденсаторов
Содержание
- 1 Расчёт конденсаторов
- 1.
 1 Расчет плоской конструкции
1 Расчет плоской конструкции - 1.2 Расчет конструкции цилиндрической формы
- 1.3 Расчёт сферической конструкции
- 1.4 Ёмкость одиночного проводника
- 1.
- 2 Способы соединения элементов
- 2.1 Параллельное соединение
- 2.2 Последовательное соединение
- 2.3 Смешанное соединение
- 3 Видео
Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.
Конденсаторы
Расчёт конденсаторов
Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:
C=q/U, где:
- C – ёмкость,
- q – заряд одной из обкладок элемента,
- U – разность потенциалов между обкладками.
В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».
Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:
Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:
С=Co*ε, где:
- С – реальная ёмкость,
- Со – идеальная, при условии, что между пластинами вакуум или воздух,
- ε – диэлектрическая проницаемость материала между ними.
Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.
Устройство конденсатора
Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).
Расчет плоской конструкции
Если нужно рассчитать плоский конденсатор, то необходимо учесть площадь обкладок и расстояние между ними. Это отражено в формуле, по которой рассчитывается ёмкость плоского конденсатора:
C=ε/d, где:
- ε – диэлектрическая проницаемость изолирующего материала,
- d – расстояние между пластинами.
Расчет конструкции цилиндрической формы
Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.
Вычисляются параметры такого устройства по формуле:
C=(2π*l*R*ε)/d, где:
- l – длина устройства,
- R – радиус цилиндра,
- ε – диэлектрическая проницаемость изолятора,
- d – его толщина.
Расчёт сферической конструкции
Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:
C=(4π*l*R1*R2*ε)/(R2-R1), где:
- R1 – радиус внутренней сферы,
- R2 – радиус внешней сферы,
- ε – диэлектрическая проницаемость.
Формулы ёмкости конденсаторов различной формы
Ёмкость одиночного проводника
Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников.
C=Q/φ, где:
- Q – заряд,
- φ – потенциал проводника.
Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.
Способы соединения элементов
Что измеряется в фарадах
Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.
Соединение конденсаторов
Параллельное соединение
Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.
При таком соединении напряжение на контактах всех элементов будет одинаковым.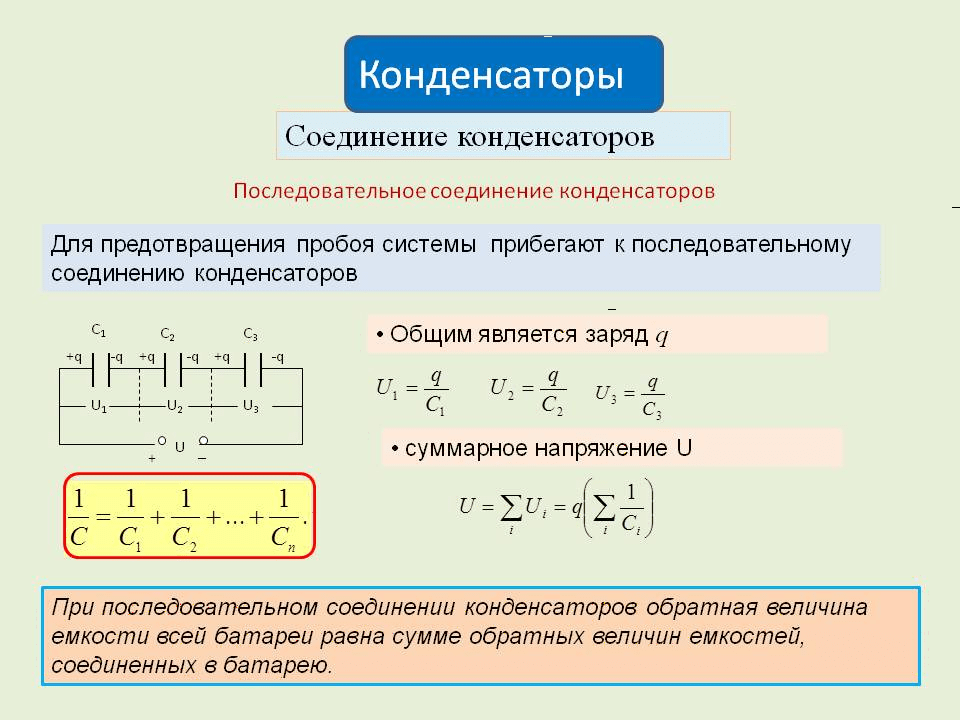 Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:
Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:
C=C1+C2+…Cn,
где C1-Cn – параметры деталей, участвующих в параллельном соединении.
Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.
Последовательное соединение
Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.
При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов.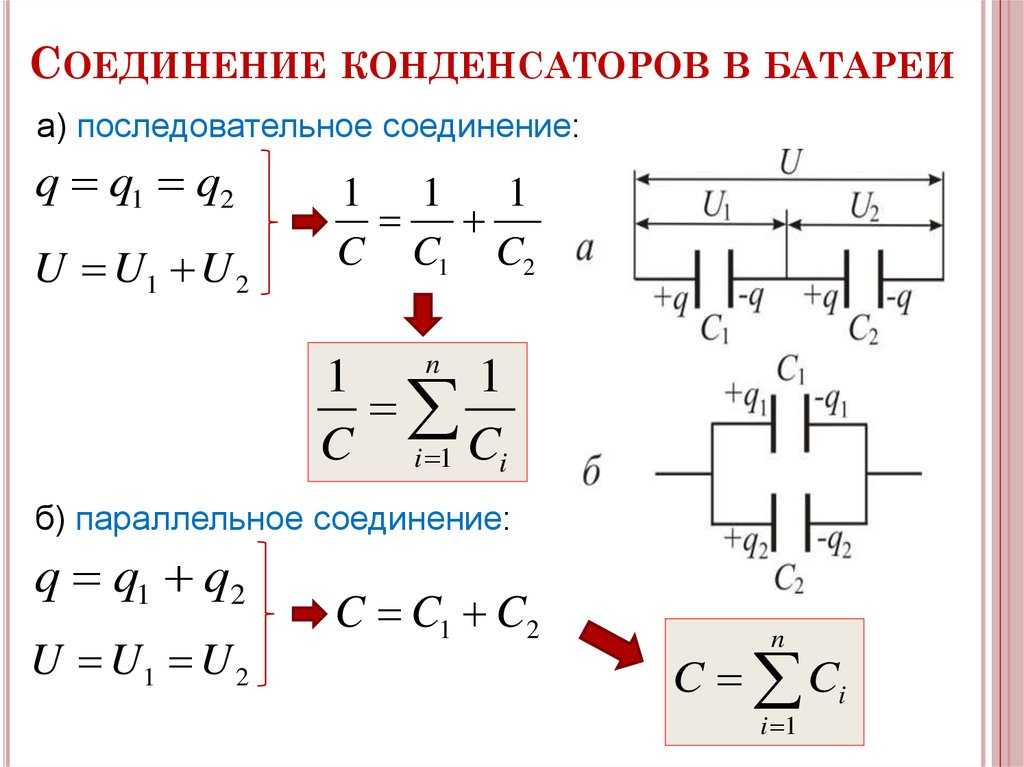
Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.
Рассчитываются эти параметры следующим образом:
- Допустимое напряжение:
Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;
- Общая ёмкость:
1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.
Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).
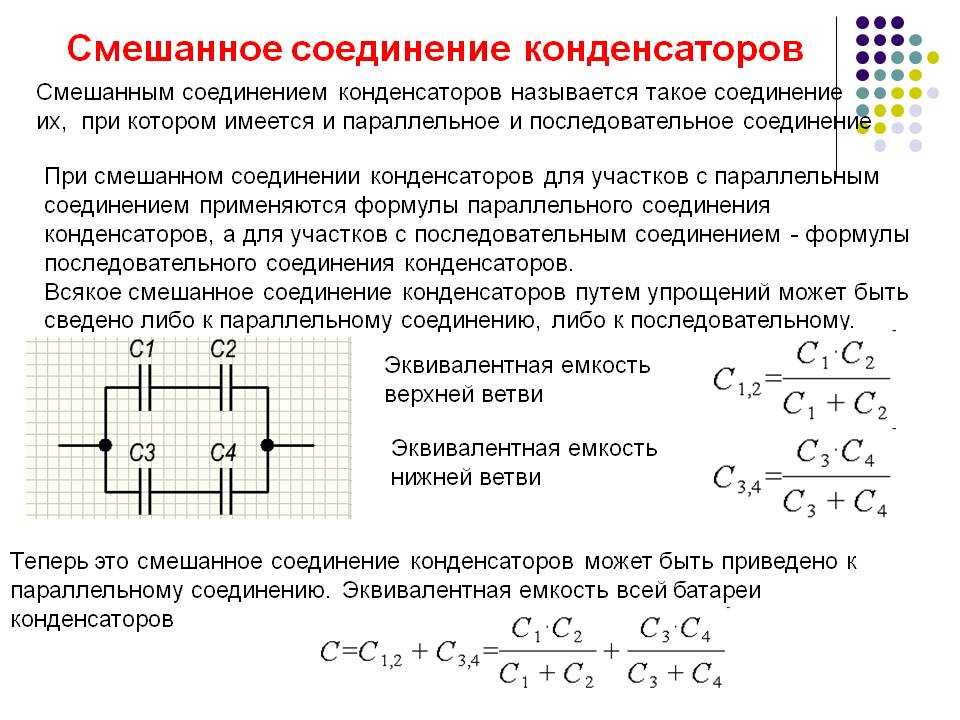
Смешанное соединение
Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:
- определяются группы элементов, соединённые параллельно;
- для каждой группы в отдельности рассчитывается эквивалентные значения;
- рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
- получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.

Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.
Видео
Оцените статью:
|
| ||||||||||||||||||||||||||||
Конденсатор и емкость – формулы и уравнения
Следующие формулы и уравнения могут быть использованы для расчета емкости и соответствующих величин конденсаторов различной формы следующим образом.
Содержание
Емкость конденсатора:Емкость — это количество заряда, накопленного в конденсаторе, на вольт потенциала между его пластинами. Емкость можно рассчитать, если известны заряд Q и напряжение V конденсатора:
C = Q/V
Заряд, накопленный в конденсаторе:Если известны емкость C и напряжение V, то можно рассчитать заряд Q. по:
Q = C V
Напряжение конденсатора:И вы можете рассчитать напряжение конденсатора, если известны две другие величины (Q и C):
В = Q/C
Где
- Q — это заряд между обкладками в кулонах
- Кл — емкость в фарадах
- В это разность потенциалов между пластинами в Вольтах
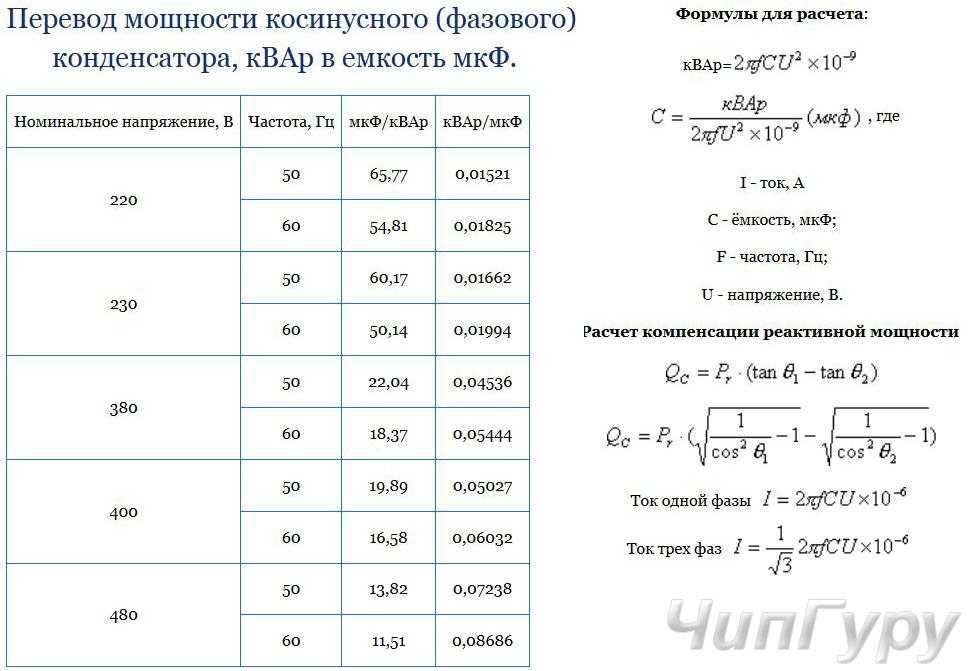
Реактивное сопротивление – это сопротивление конденсатора переменному току, которое зависит от его частоты и измеряется в Омах, как сопротивление. Емкостное реактивное сопротивление рассчитывается по формуле:
Емкостное реактивное сопротивление рассчитывается по формуле:
Где
- X C — емкостное реактивное сопротивление
- F — применяемая частота
- Кл это емкость
Коэффициент добротности или добротность – это эффективность конденсатора с точки зрения потерь энергии, которая определяется по формуле:
QF = X C /ESR
ГдеD-фактор или коэффициент рассеяния является обратным коэффициенту добротности, он показывает рассеивание мощности внутри конденсатора и определяется как:
DF = tan δ = ESR/X C
Где
- DF — коэффициент рассеяния
- δ — угол между емкостной реактивностью победителя и отрицательной осью.

- X C — емкостное реактивное сопротивление .
- ESR — эквивалентное последовательное сопротивление цепи.
Похожие сообщения:
- Емкость и индуктивность из калькулятора реактивного сопротивления
- Почему ток увеличивается при увеличении емкости или уменьшении емкостного реактивного сопротивления?
Энергия E, запасенная в конденсаторе, определяется по формуле:
E = ½ CV 2
Где
- E — энергия в джоулях
- Кл — емкость в фарадах
- В это напряжение в вольтах
Средняя мощность конденсатора дается:
P AV = CV 24/ 2T 9024 Когда конденсатор заряжается через резистор R, для полного заряда требуется до 5 постоянных времени или 5 Тл. Напряжение в любой момент времени можно найти с помощью следующих формул зарядки и разрядки: Напряжение конденсатора в любой момент разрядки определяется по формуле: Где Похожие сообщения: Емкость между двумя проводящими пластинами с диэлектриком между ними можно рассчитать по формуле: Где Где: C 2 ≈ (0,256479 ч 2 + 1,57292 r 2 ) pF Где: C 2b ≈ 4πε o r Где: 9002 r 90 Где: Q = CV Дифференцируя уравнение, получаем: где 9024 2 9024 9024 9024 9024 9024 9024 9024 9024 9024 9024 9024 9024 9024 9024 9024 9024 9024 9024 .  секунды. Напряжение конденсатора во время зарядки/разрядки:
секунды. Напряжение конденсатора во время зарядки/разрядки:
Формулы емкости
Емкость пластинчатого конденсатора Формула
Собственная емкость катушки (формула Медхерста)
Формула собственной емкости сферы
Закон Ома для конденсатора:


 Изначально были конденсаторы.
называемые «конденсаторами» по причине, которая восходит ко временам Лейденской банки, где считалось, что электрические заряды
накапливаться на тарелках в результате процесса конденсации.
Изначально были конденсаторы.
называемые «конденсаторами» по причине, которая восходит ко временам Лейденской банки, где считалось, что электрические заряды
накапливаться на тарелках в результате процесса конденсации. В последовательной цепи полное сопротивление току на резонансной частоте
равен нулю с идеальными компонентами. В параллельной цепи (справа) полное сопротивление протеканию тока бесконечно с идеальными компонентами.
В последовательной цепи полное сопротивление току на резонансной частоте
равен нулю с идеальными компонентами. В параллельной цепи (справа) полное сопротивление протеканию тока бесконечно с идеальными компонентами. Следовательно, необходимо тщательное рассмотрение SRF, когда
подбор конденсаторов. Симуляторы типа SPICE используют эту или еще более сложную модель для облегчения более точных расчетов.
в широком диапазоне частот.
Следовательно, необходимо тщательное рассмотрение SRF, когда
подбор конденсаторов. Симуляторы типа SPICE используют эту или еще более сложную модель для облегчения более точных расчетов.
в широком диапазоне частот.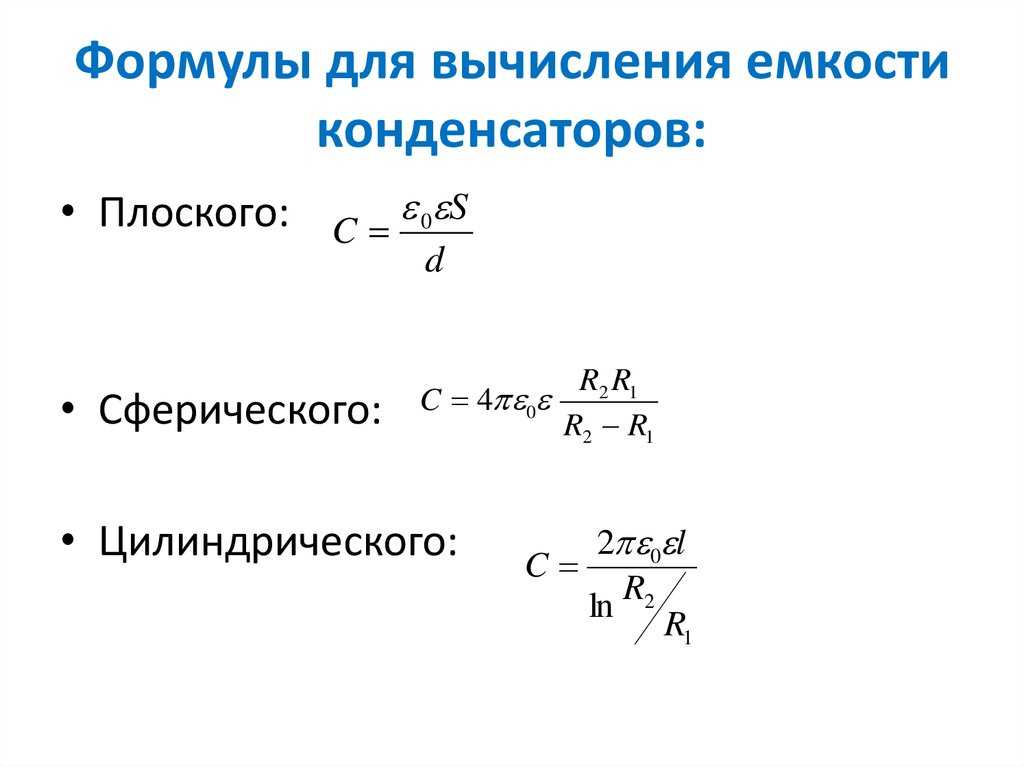 Сохраняйте единицы измерения постоянными.
Сохраняйте единицы измерения постоянными. (Х С ). Это мера скорости потери накопленного заряда. DF обычно используется в низкочастотных приложениях, в то время как
тангенс δ чаще используется в высокочастотных приложениях.
(Х С ). Это мера скорости потери накопленного заряда. DF обычно используется в низкочастотных приложениях, в то время как
тангенс δ чаще используется в высокочастотных приложениях.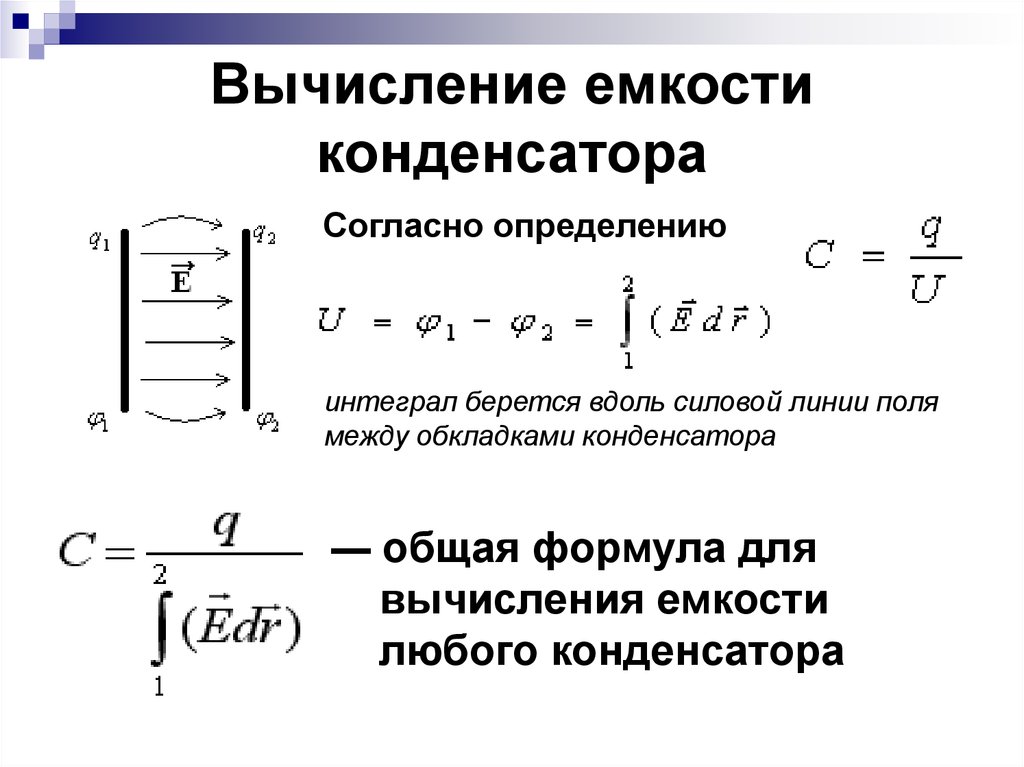 во избежание двусмысленности.
во избежание двусмысленности. на тарелках.
на тарелках. 2 МБ. Его основная цель состояла в том, чтобы предоставить мне быстрый доступ к обычно необходимым
формулы и справочный материал при выполнении моей работы в качестве радиочастотной системы и схемы
инженер-проектировщик. Всемирная паутина (Интернет) была в значительной степени неизвестной сущностью в то время.
время и пропускная способность были дефицитным товаром. Модемы с коммутируемым доступом стремительно развивались со скоростью 14,4 кбит/с
привязывая вашу телефонную линию, и приятный женский голос объявил: «У вас есть
Mail», когда пришло новое сообщение…
2 МБ. Его основная цель состояла в том, чтобы предоставить мне быстрый доступ к обычно необходимым
формулы и справочный материал при выполнении моей работы в качестве радиочастотной системы и схемы
инженер-проектировщик. Всемирная паутина (Интернет) была в значительной степени неизвестной сущностью в то время.
время и пропускная способность были дефицитным товаром. Модемы с коммутируемым доступом стремительно развивались со скоростью 14,4 кбит/с
привязывая вашу телефонную линию, и приятный женский голос объявил: «У вас есть
Mail», когда пришло новое сообщение…