Вычисляем площадь квадрата: по стороне, диагонале, периметру
Площадь квадрата – базовое понятие, благодаря которому можно без проблем рассчитать расход материалов для ремонта, высчитать верные габариты мебели при замерах помещения, понять, сколько нужно удобрения и семян для высадки важных культур на огромном поле.
Приведенными формулами площади квадрата пользуются и строители, и мебельные производители, и представители сельского хозяйства.
Что такое квадрат?
Квадрат – правильный прямоугольник с равными сторонами. Каждый угол фигуры равен 90⁰. Квадрат относится к простым геометрическим фигурам, расположенным на плоскости. Найти площадь квадрата можно несколькими способами вычислений: по диагонали, по стороне, по периметру.
Формулы площади, примеры расчетов
Площадь простой фигуры – положительная величина, обладающая перечисленными ниже свойствами:
- Равные геометрические фигуры обладают равными площадями.
- В случае, если простая фигура разделена на несколько частей, ее общая площадь будет всегда равна сумме площадей всех элементов.
- Площадь квадрата всегда равна единице, если его сторона соответствует единице измерения.
По стороне
В геометрии площадь всегда обозначается как S, а маленькие латинские буквы (например, а и b) – это стороны простой фигуры.
В основе вычисления площади любого прямоугольника по стороне лежит простая формула: S = ab , но в случае с квадратом формулу преобразовывают в S = а² , так как две стороны одинаковы по длине.
Отсюда следует утверждение, что площадь квадрата равна квадрату его стороны.
Пример 1: Дан квадрат, сторона которого равна 5 см. Чему равна площадь?
Решение: S = 5² = 25 см
Пример 2: Сторона фигуры 3 см. Найдите площадь.
Решение: S = 3² = 9 см
По диагонали
Еще один вариант найти площадь – это произвести вычисления относительно диагонали фигуры (d). Правда, для этого нужно сперва найти длину самой диагонали. Известно, что диагональ делит квадрат на два равнобедренных треугольника.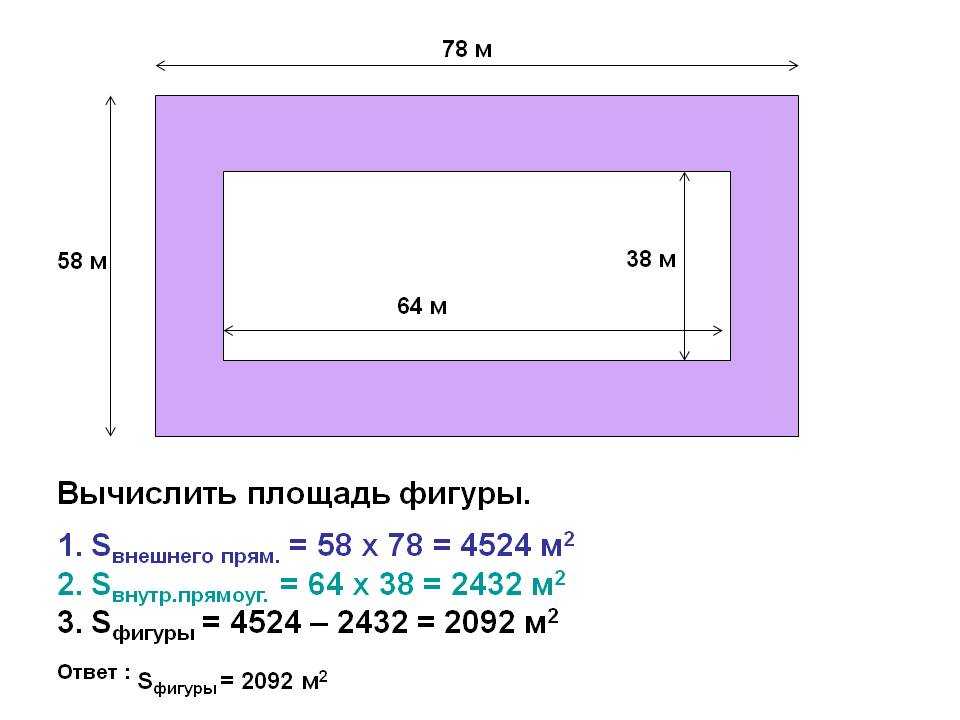
Расчет площади по диагонали производится по принципу: площадь квадрата равна квадрату длины диагонали (вычисленной по теореме Пифагора) и поделенному на два.
Пример: Дан квадрат, диагональ которого составляет 10 см. Как вычислить площадь?
Решение: Согласно формуле, приведенной выше, вычисления производятся так: S = 10²/2 = 100/2 = 50 cм²
По периметру
Периметр – сумма всех длин сторон квадрата. Обозначается периметр латинской буквой Р. Беря во внимание определение квадрата, получаем универсальную формулу расчета периметра для равностороннего четырехугольника:
Вычисления площади квадрата относительно суммы всех сторон необходимо в том случае, если в задаче задано только значение периметра.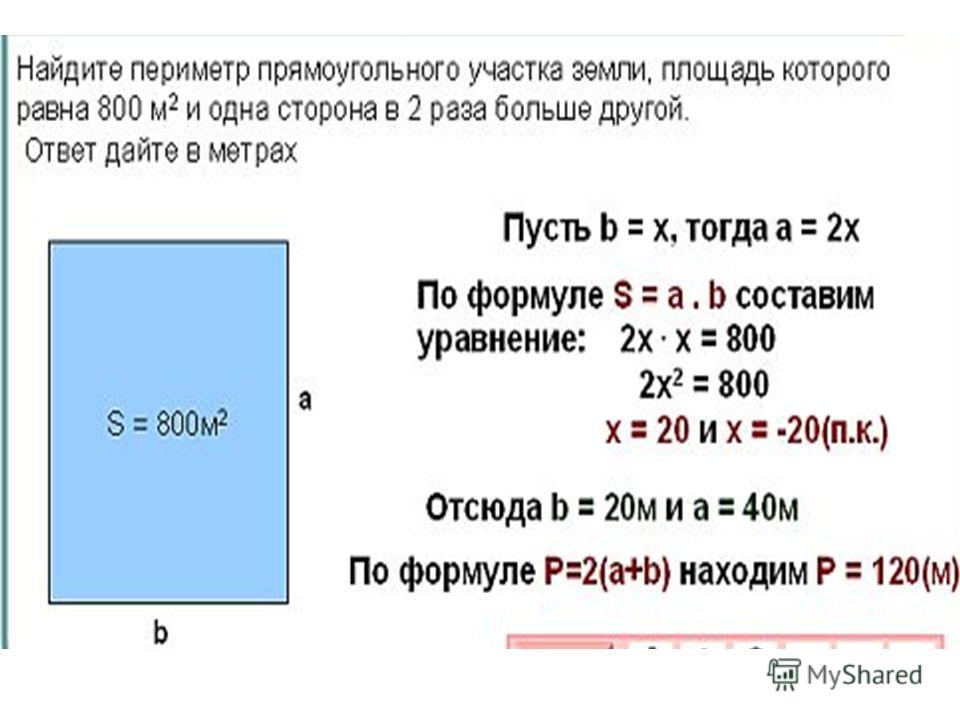
Зная формулу вычисления периметра, очень легко найти площадь.
Если Р = 4а , то а = Р/4 . Далее уже нужно использовать формулу расчета площади по стороне.
Решение: Сторона квадрата будет равна 100/4 = 25 мм. Ну, а площадь квадрата дальше вычисляется по формуле, где площадь квадрата равна квадрату сторон. То есть, S = 25² = 625 мм²
Площадь квадрата вписанного в окружность
Этот вариант используется как следствие формулы, полученной ранее (расчет по диагонали). Согласно математическим данным, диаметр круга как раз и будет равен диагонали квадрата. Поэтому, чтобы оперативно рассчитать площадь равностороннего четырехугольника, достаточно будет знать диаметр круга. А далее используется уже известная формула: S = d²/2
Типовая задача: например, дана окружность с диагональю 8 см и в нее вписан квадрат. Какая площадь четырехугольника?
Видео урок
youtube.com/embed/n2DuIBjJFIo» frameborder=»0″ allowfullscreen=»»> § Площадь фигур. Площадь квадрата. Площадь прямоугольника. Площадь сложной фигуры
Определение площади Формулы площадей фигур
Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная определение степени, можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.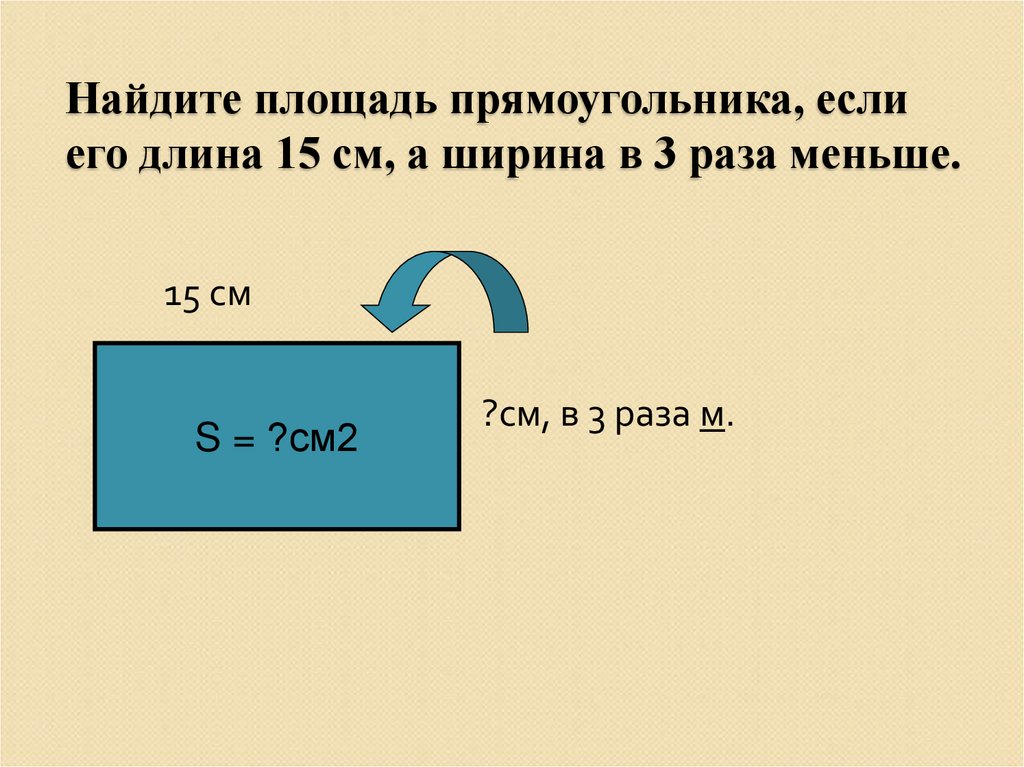
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + S
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.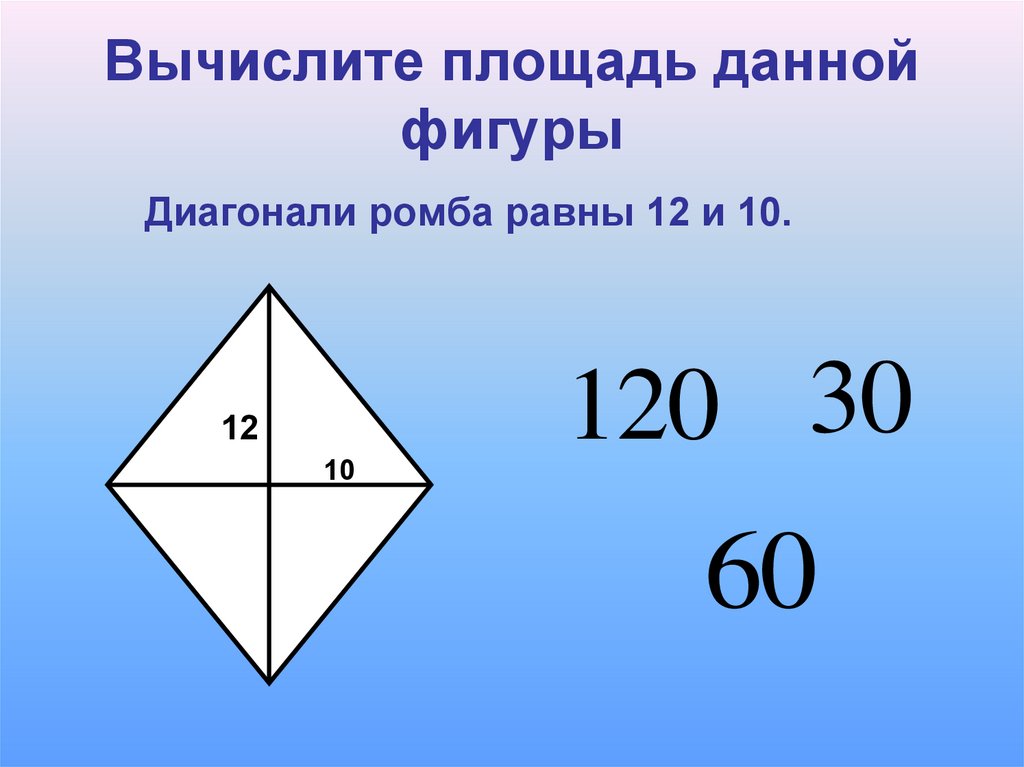
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника ABCD. Найдём площадь треугольников ABC и ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S ABC = SABCD : 2
S ABC = 20 : 2 = 10 см2
S ABC =
S ACD = 10 см2
Определение площади Формулы площадей фигур
Калькулятор площади прямоугольника
Длина(a)
Ширина(b)
Площадь(A)
Периметр(P)
Диагональ(d)
Перейти к вычислению площади прямоугольника
Площадь прямоугольника
Перейти к периметру прямоугольника
Перейти к вычислению периметра прямоугольника
Перейти к диагонали прямоугольника
Перейти к вычислению диагонали прямоугольника
Перейти к их практическому применению Расчеты
Вернуться на страницу калькуляторов
Как вычислить площадь прямоугольника Если вам нужно найти площадь и периметр прямоугольника, этот калькулятор — удобный инструмент, который вам понадобится.
Просто введя длину и ширину, этот калькулятор почти мгновенно найдет периметр (P) и площадь (A).
Если вас интересуют калькуляторы для различных других форм, вы можете посмотреть другие наши удобные калькуляторы. Но вы можете остаться здесь и узнать больше о нахождении площади прямоугольника.
Прямоугольник имеет четыре угла по 90 градусов. Если длины всех сторон одинаковы, то прямоугольник также является квадратом. Длины сторон будут указаны как a или b , или вы можете использовать l и w для «длины» и «ширины». Диагональ, идущая от одной вершины к противоположной, делящей прямоугольник на два квадрата, называется диагональю и обозначается как d .
Вот основные формулы, используемые калькулятором.
Площадь(A) = a(b)
Периметр (расстояние вокруг внешней стороны прямоугольника) = a + a + b + b или 2 a + 2
0 b и обозначается как (P) Диагональ равна d ² = a ² + b ², что является теоремой Пифагора (см.
наш калькулятор теоремы Пифагора).
Пример вычисления площади прямоугольника:
Предположим, что длина равна а = 6 дюймов, а ширина равна b = 4 дюйма
A = a * b , поэтому A = 6(4) = 24 дюйма²
Используя те же размеры, мы можем вычислить периметр.
Периметр равен 2 a + 2 b , поэтому в этом примере периметр
P = 2(6) + 2(4) = 20 дюймов
Чтобы найти диагональ, используя те же размеры:
d ² = 6² + 4² = 36 + 16 = 52
Возьмите квадратный корень из обеих сторон, и диагональ d будет приблизительно 7,2 дюйма
Эти примеры иллюстрируют, как вычислить площадь, периметр и диагональ прямоугольника вручную, но если вы предпочитаете использовать калькулятор для получения более быстрых результатов или просто для проверки своей работы, не стесняйтесь делать это. Отличительной особенностью калькулятора является то, что вы можете найти либо длину, либо ширину, если знаете периметр и длину одной из сторон.
На этой странице показано, как измерять площадь прямоугольника. Мы рассмотрим следующие темы:
Каковы площадь, периметр и диагональ прямоугольника?
Как вычислить площадь, периметр и диагональ прямоугольника?
Реальное приложение для вычисления площади, периметра и диагонали прямоугольника
Площадь прямоугольникаПредставьте площадь прямоугольника в виде клеток внутри прямоугольника. Прямоугольник ниже имеет покрытую площадь 12 «квадратов»
Пространство внутри двумерной формы — это площадь или количество закрытой формы.
На этой диаграмме показаны ширина, длина и площадь прямоугольника:
Вычисление площади прямоугольника
Чтобы найти площадь прямоугольника, нужно умножить длину и ширину прямоугольника.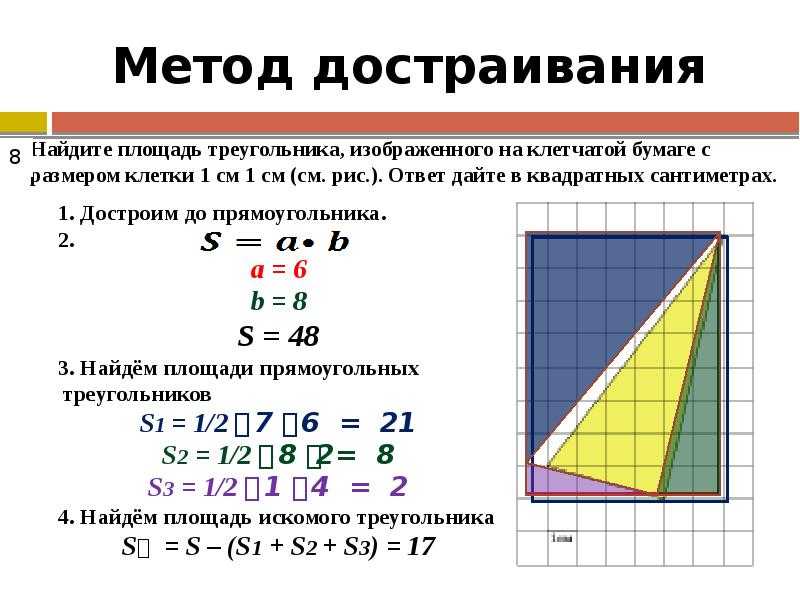
. Мы можем получить площадь прямоугольника по следующей формуле:
A = L * W
A — площадь, L — длина, W — ширина.
Пример 1Вычислите площадь прямоугольника, имеющего длину 7 сантиметров и ширину 5 сантиметров.
Формула:A = L * W
Ответ:A = 35. Данная длина ( L ). W ). При умножении вы получите 35 в качестве вашей площади.
Периметр прямоугольникаПосмотрите на изображение ниже, человек ходит вокруг коробки. Путь, который он проходит от начальной точки и обратно, является периметром. Зная длину и ширину прямоугольника, мы можем теперь получить периметр прямоугольника. Обе противоположные стороны прямоугольника конгруэнтны, что означает, что сложив эти стороны, мы можем вычислить периметр.
Вычисление периметра прямоугольника
Сложив все стороны прямоугольника, мы теперь можем получить его периметр.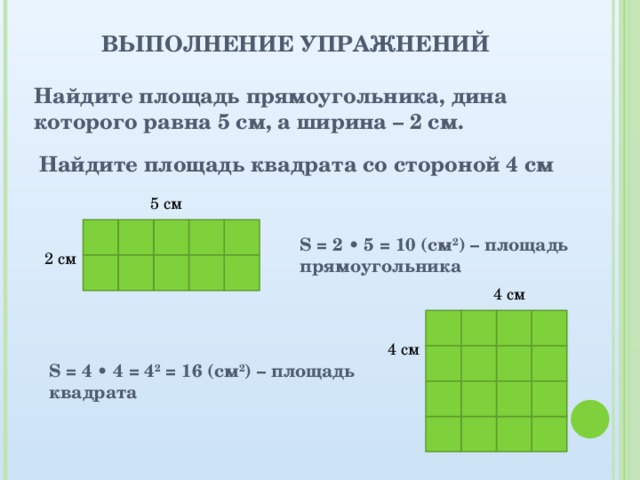
Вот уравнение для получения периметра прямоугольника:
P = L + W + L + W
Поскольку мы знаем, что обе противоположные стороны прямоугольника идентичны, мы можем упростить уравнение, используя это уравнение :
P = 2L + 2W
Пример 1Найдите периметр прямоугольника, длина которого 12 сантиметров, а ширина 7 сантиметров.
Формула:P = L + W + L + W или
P = 2L + 2W
9
Ответ: 9004 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 . 12 + 7 илиP = 2(12) + 2(7)
Ответ будет P = 38.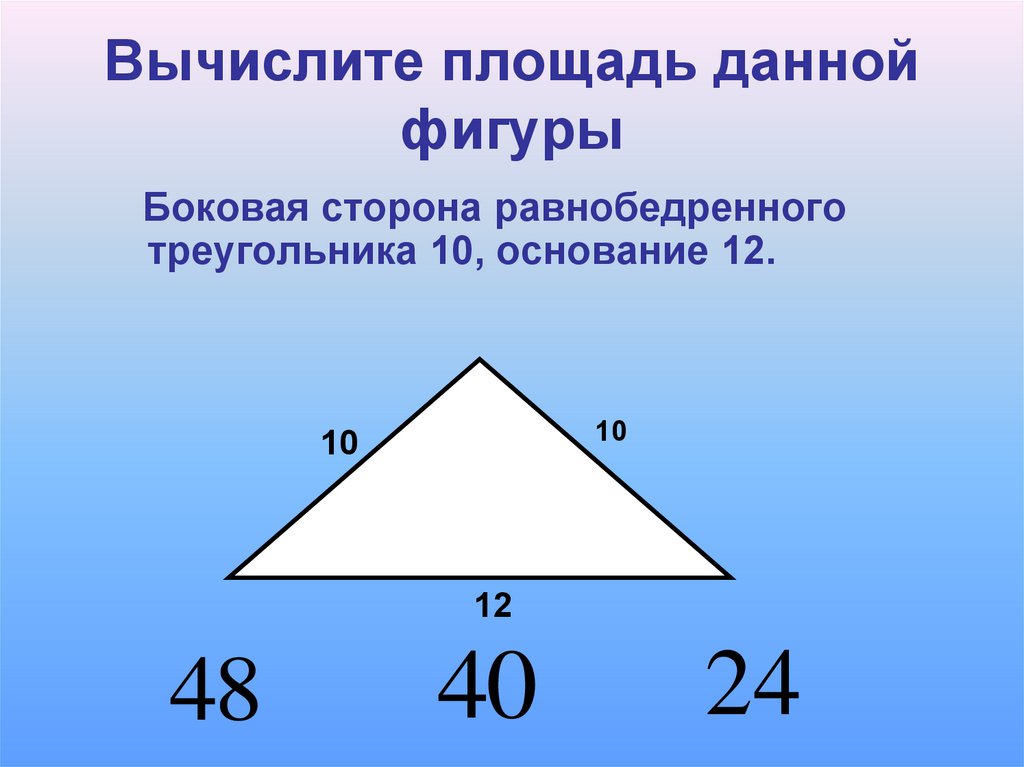
Прибавив 12 ( L ) + 7 ( W ) + 39 (
Если присмотреться, прямоугольник представляет собой комбинацию двух прямых углов. Диагональ — это деление прямоугольника на два одинаковых прямоугольных треугольника.
Вычисление диагонали прямоугольника
Мы знаем, что прямоугольник представляет собой комбинацию двух прямоугольных треугольников. Диагональ этого прямоугольника равна 9.{2}}\) \(D = \sqrt{289}\)
D = 17
Диагональ прямоугольника равна 17. Возведите в квадрат значения ширины (W) и длины (L), затем получите сумму из двух квадратов. Зная сумму двух квадратов, найдите квадратный корень из суммы.
Вычислите длину диагонали прямоугольника длиной 5 футов и шириной 3 фута.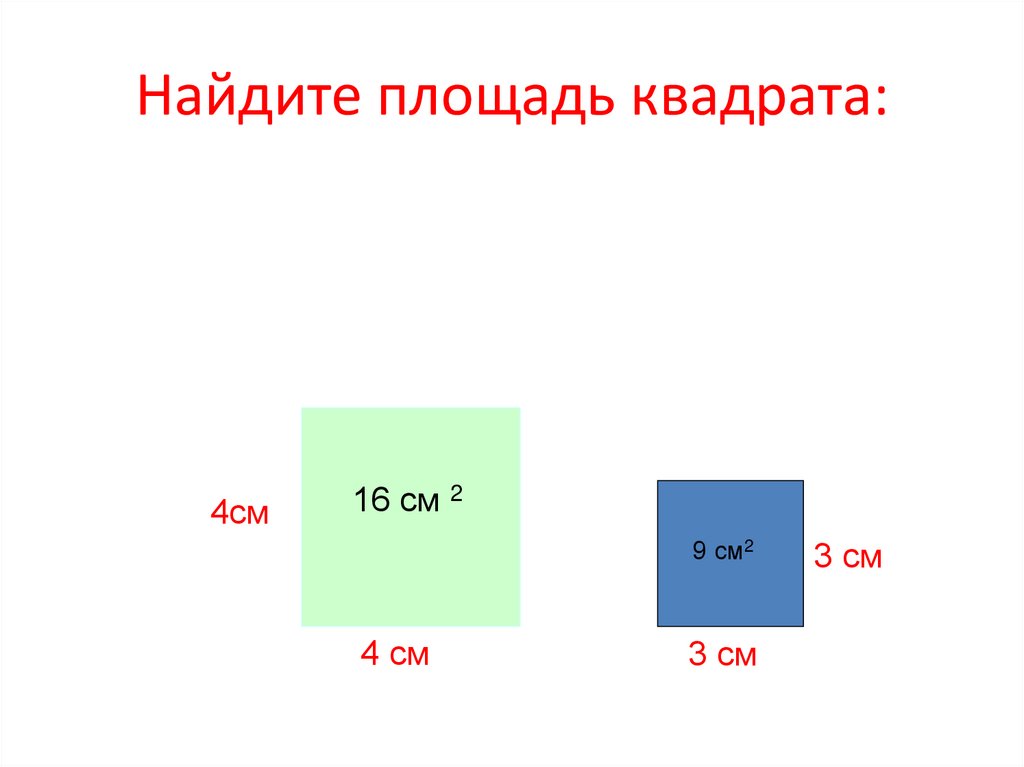
{2}}\)
\(D = \sqrt{34}\)
D = 5,83
Реальные приложения для получения площади прямоугольникаМолодожены хотят положить плитку на пол в главной спальне. Комната имеет длину 20 футов и ширину 30 футов. Плитка, которую они выбрали, имеет длину 24 дюйма и ширину 36 дюймов. Решите, сколько плиток нужно, чтобы заполнить главную спальню.
Советы:
1. Найдите площадь, занимаемую главной спальней.
2. Вычислите площадь плитки
3. Выберите единицу измерения. В этом примере будут использоваться ноги.
Solution:A = L * W
A = 20 ft x 30 ft
A = 600 ft²
Tip:
Прежде чем мы получим площадь каждой плитки, переведем футы в дюймы
Пример преобразования:
1 Фут = 12 дюймов
2 фута = 24 дюйма
3 фута = 36 дюймов
Площадь 1 Tile = L × W
999999999999999999999999999999999999999999999999999999999999999999999999999999999н = 2 × 3Площадь 1 плитки = 6 футов²
Это означает, что каждая плитка имеет площадь 6 футов² и должна покрывать площадь комнаты, которая составляет 600 футов².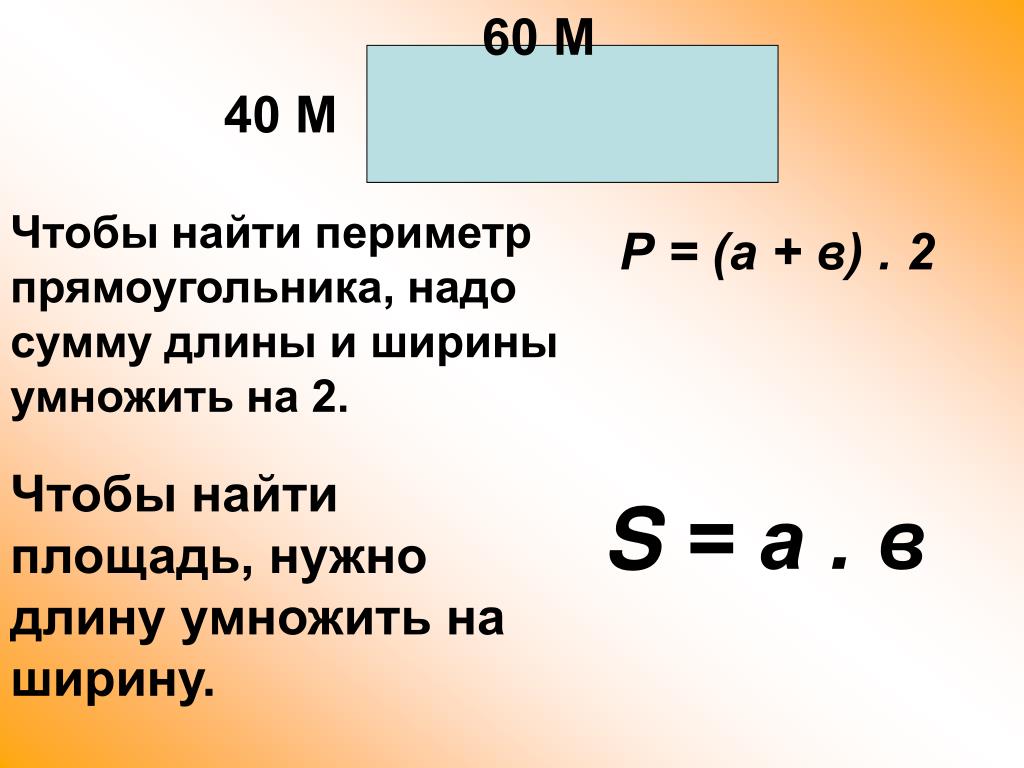
Итак, 6 × 100 = 600,
Количество плиток, необходимых для заполнения главной спальни, составляет 600.
Реальные приложения для получения периметра прямоугольникаФермер хочет добавить клетку для своих цыплят. Он хочет добавить новый забор возле своего дома и свободное пространство длиной 30 метров и шириной 16 метров. Найдите периметр свободного пространства.
Решение:P = 2L + 2W
Ответ:Периметр = 2(длина свободного пространства) + 2(ширина свободного пространства)
P = 2(30) + 2(16)
0 P = 63 9 + 32
P = 92
Периметр свободного пространства 92 метра.
Реальные приложения для получения диагонали прямоугольника Бутерброд имеет длину 12 дюймов и ширину 8 дюймов.
Если вы хотите поровну разделить его на два прямых угла, какова будет длина диагонали? 9{2}}\)
\(D = \sqrt{236}\)
D = 14,42
должно быть 14,42 дюйма.
Как рассчитать площадь?
Геометрия рассматривается в школе как набор формул, отвечающих на вопрос, как вычислить площадь? Геометрия — это гораздо больше: она включает в себя всю часть математики, которая решает проблемы пространства, отвечает на вопросы о форме плоских и трехмерных фигур и, идет гораздо дальше, пытаясь ответить на вопрос о форме нашей Вселенной… Но давайте не будем заходить так далеко, прежде чем ответить на этот вопрос, важно, чтобы мы знали, что мы имеем в виду, когда спрашиваем себя о площади многоугольника.
Путаница между площадью и периметром
Когда нас спрашивают о площади, нас спрашивают о поверхности, а не о том, что ее окружает. Очень типичная путаница заключается в том, что вместо измерения или расчета поверхности мы измеряем «то, что ее окружает», периметр.
В прямоугольной картине с тонкой металлической или деревянной рамой площадь будет окрашенной частью, холстом или бумагой, а периметром будет длина рамы.
В видео ниже используется другой пример, огород с несколькими поверхностями, на которых будут высаживаться разные культуры. В их вершинах размещаются колья, а веревки ограничивают их. В этом сценарии длина этих веревок будет периметром.
Периметр всегда является мерой длины.
Видеоруководство по вычислению периметра любой фигуры
В этом видеоруководстве Smartick вы можете простым способом научиться вычислять периметр любой фигуры.
Разобравшись, надеюсь, с возможной путаницей, рекомендую прочитать: Как вычислить периметр? Если это то, что вас интересует.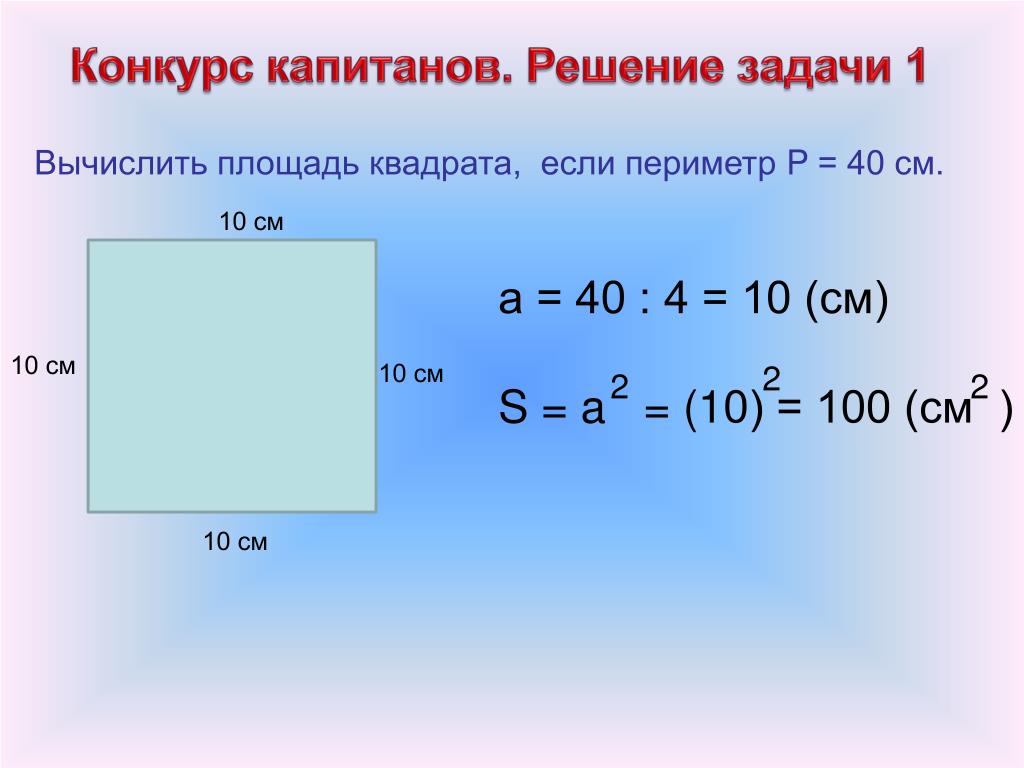
Как вычислить площадь многоугольника на сетке?
Если многоугольник, площадь которого вы хотите узнать, находится в сетке, существует очень простой способ вычислить его площадь: посчитайте квадраты, которые он покрывает. Но будьте осторожны, площади являются мерами поверхности, поэтому вы также должны указать единицы измерения. Это могут быть квадратные метры, квадратные сантиметры… они всегда будут квадратными единицами, потому что они исходят из квадратного счета, о котором мы писали.
Теперь посмотрите на следующий пример, потому что есть деталь, которую вы не можете упустить:
Под сеткой есть маленький квадрат, который говорит нам, сколько измеряет каждый квадрат, это легенда этой фигуры, и говорит нам, что каждый квадрат равен одному квадратному сантиметру . Но оно могло быть и другим и могло быть равно квадратному метру (если это был план комнаты) или квадратному километру (если это была карта региона), а могло быть так, что каждый квадрат был равен 2 см² и тогда площадь прямоугольника будет 28 на 2, 56 см².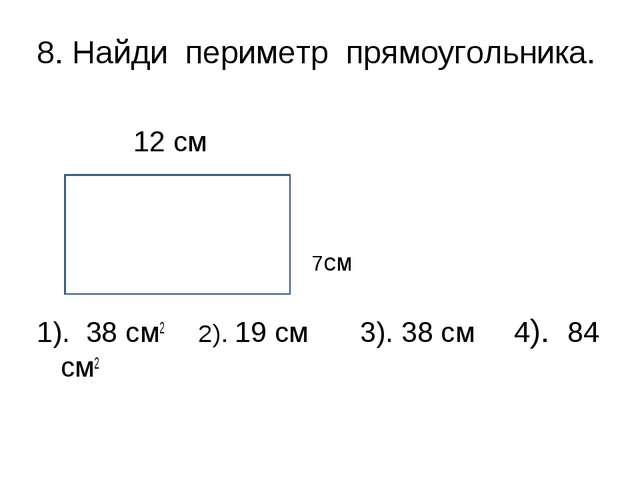
Этот простой способ ответить, как вычислить площадь, можно применить, когда фигура состоит из нескольких многоугольников, что называется составным многоугольником. Как в примере ниже:
В этом случае нам придется считать квадраты и полуквадраты.
Как вычислить площадь прямоугольника?
Подсчет квадратов — это хорошо, но если квадратов много, вы можете пропустить некоторые из них или пересчитать их дважды. Если фигура, площадь которой вы хотите узнать, представляет собой прямоугольник размером есть более быстрый способ. Подумайте об этом, в прямоугольниках квадраты организованы в строки и столбцы. Итак, если вы хотите узнать, сколько там квадратов, вам просто нужно… умножить количество строк на количество столбцов!
Что делать, если внизу нет сетки, но вы знаете ширину и высоту прямоугольника? Ну, так как нужно было посмотреть, сколько единичных квадратов было в прямоугольнике, их будет столько, сколько произведение ширины на высоту, знаменитое основание на высоту.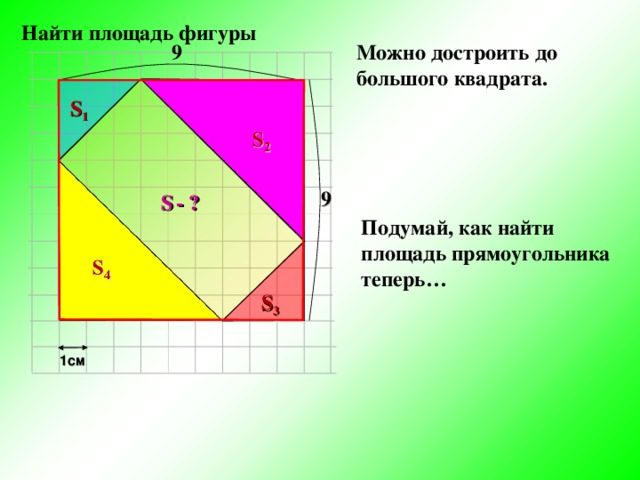
Вы должны убедиться, что оба измерения находятся в одной и той же единице, то есть в сантиметрах, в дециметрах, в метрах… Таким образом, вы также сможете узнать единицы площади: квадратные сантиметры, квадратные дециметры или что угодно, но квадратные.
Площадь прямоугольника= основание × высота
Как вычислить площадь прямоугольного треугольника?
Самый простой случай — прямоугольный треугольник. Вдумайтесь, прямоугольный треугольник — это половина прямоугольника, который делится своей диагональю.
Как мы уже знаем из предыдущего раздела, площадь прямоугольника вычисляется путем умножения основания на высоту, площадь треугольника будет равна половине этого произведения. Если расстояние между двумя стержнями геоплана на нашем рисунке равно 1 сантиметру, прямоугольник будет иметь 3 × 6 = 18 см², а треугольник будет иметь половину, ровно 9 см².
Кстати, для рисования мы использовали этот онлайн-геоплан, на случай, если вы захотите использовать его для тестирования.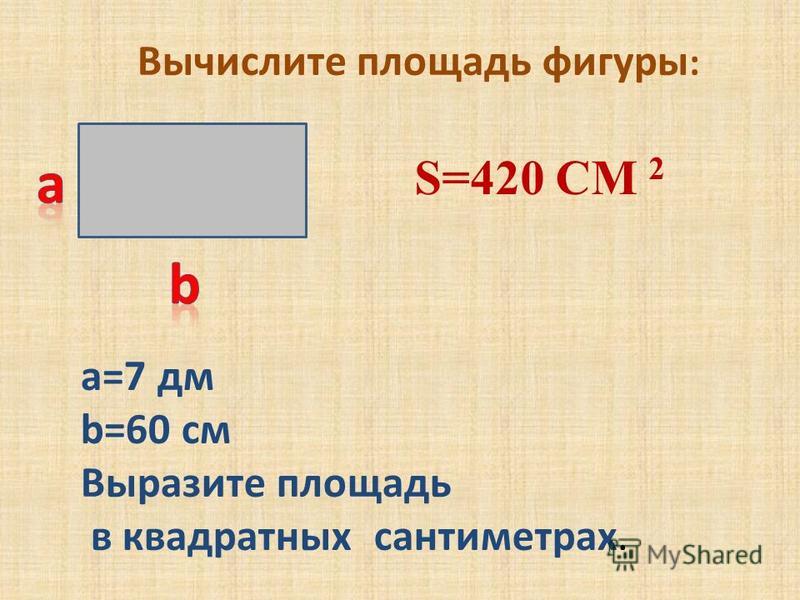
Площадь прямоугольного треугольника = (основание × высота) ⁄ 2
Эта формула будет полезна для вычисления площади и непрямоугольных треугольников, но если вы хотите узнать причину, вам придется прочитать раздел об этом.
Как вычислить площадь ромбоида?
Ромбоид – это четырехугольник, стороны которого параллельны попарно. Например, вот этот:
Если подумать, любой бумажный ромб можно преобразовать с помощью ножниц, вырезав прямоугольный треугольник и переместив его на противоположный конец.
Получился прямоугольник! Таким образом, прямоугольник и ромб используют один и тот же способ вычисления площади, основанной на высоте.
Площадь ромба = основание × высота
Как вычислить площадь треугольника, который не является прямоугольным?
Как остроугольные, так и тупоугольные треугольники можно рассматривать как полуромбы. Если вы скопируете и вставите треугольник рядом, вы сможете проверить его.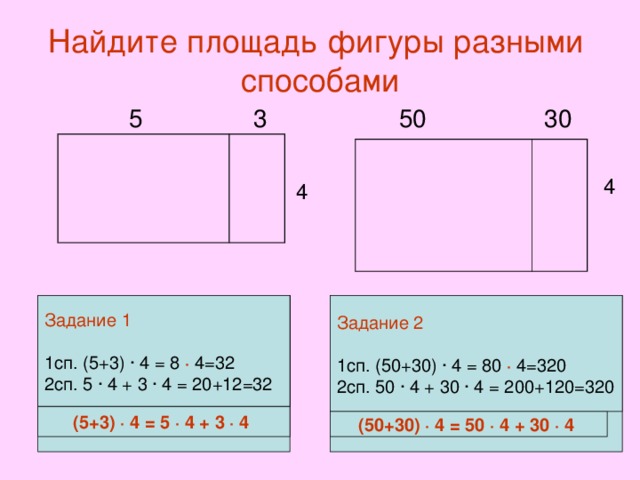
Следовательно, и поскольку площадь ромбоида равна основанию, умноженному на высоту, площадь этих треугольников — и любого треугольника — равна основанию, умноженному на высоту, умноженную на два:
Площадь любого треугольника = (основание × высота) ⁄ 2
Как вычислить площадь трапеции?
Трапеция — это четырехугольник с двумя параллельными сторонами и двумя основаниями, как этот:
Если вы хотите узнать площадь трапеции, проще всего это сделать… то же самое мы сделали с треугольники! Просто скопируйте трапецию в сторону, и она станет ромбом!
Основание этого ромба равно сумме двух оснований трапеции, а высота остается неизменной. Таким образом, площадь ромбоида будет (основание 1 + основание 2) × высота и, поскольку трапеция является половиной ромбоида:
Площадь трапеции = [(основание 1 + основание 2) × высота] ⁄ 2
Как вычислить площадь ромба?
Ромб – это четырехугольник, у которого четыре стороны равны.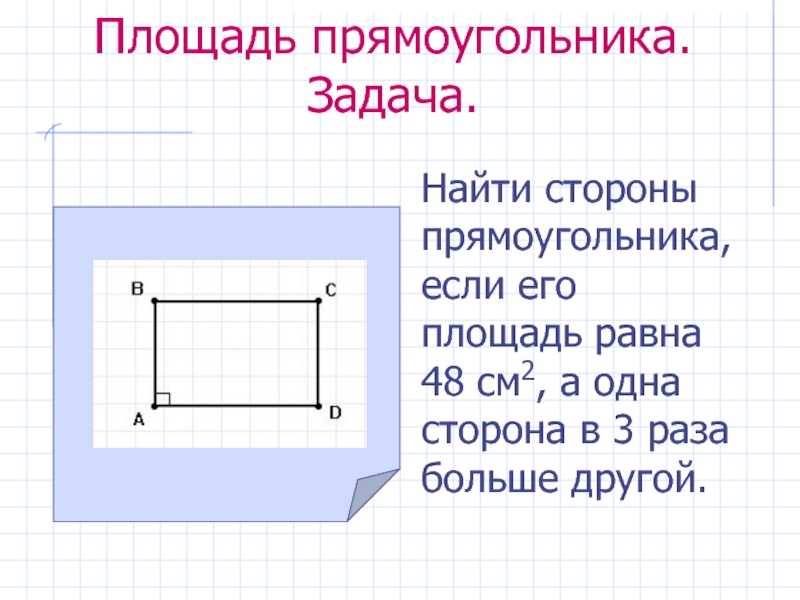
Кстати, у квадратов 4 равные стороны. Таким образом, мы можем думать о квадратах как о «предельных случаях» ромбов. Но для этой записи нас интересует ромб, который выглядит примерно так:
Чтобы вычислить площадь ромба, нужно знать длину его диагоналей. Мы будем называть D длинной диагональю, а d короткой диагональю (которые являются вертикальной и горизонтальной линиями на чертеже соответственно).
На изображении уже виден возможный способ вычисления площади ромба. Вы можете сделать это, вычислив площадь четырех одинаковых треугольников, образованных диагоналями.
Площадь любого из этих треугольников будет равна основанию, умноженному на высоту, деленному на два. Его основание составляет половину диагонали d, а высота — половину диагонали D. Следовательно, площадь одного из этих треугольников равна D, умноженному на d, деленное на 8. А так как таких треугольников у нас 4, площадь ромба равна:
Площадь ромба = (D по диагонали × d по диагонали) ⁄ 2
Как вычислить площадь правильного многоугольника с более чем 4 сторонами?
У правильного многоугольника все стороны равны, равно как и все углы.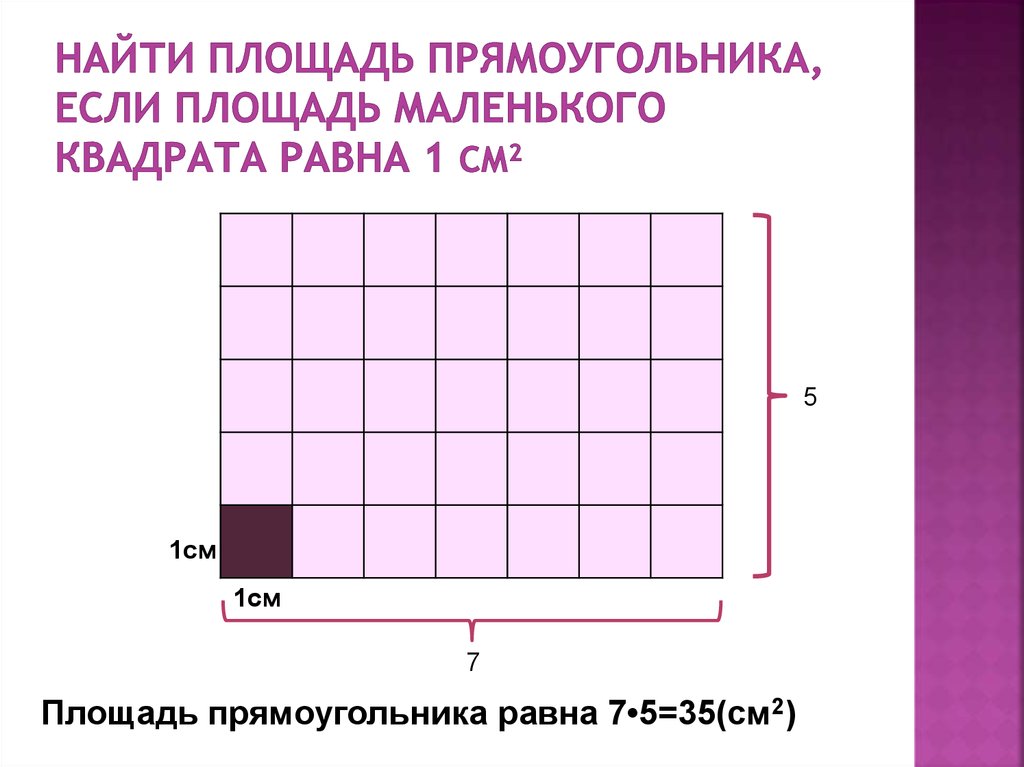
Например, посмотрите на следующий семиугольник, правильный многоугольник с 7 сторонами:
Чтобы вычислить его площадь с помощью инструментов начальной или средней школы, вам нужна длина его стороны (любой из них, они ВСЕ равны) и его апофема, которая представляет собой линию, соединяющую центр многоугольника с половиной стороны. В семиугольнике мы могли бы нарисовать 7 таких сегментов, но все они были бы одинакового размера.
Обратите внимание, что произойдет, если соединить пару последовательных вершин многоугольника с центром:
Образуется равнобедренный треугольник (в случае шестиугольника это будет равносторонний треугольник), основанием которого является сторона многоугольника и как высота апофема многоугольника. Многоугольник состоит из треугольников, равных количеству сторон, в нашем случае 7.
Площадь одного из этих треугольников будет равна стороне, умноженной на апофему, деленной на два. А так как треугольников у нас 7, то общая площадь будет 7 умножить на сторону умножить на апофему разделить на два.
Но подождите, разве сторона, умноженная на 7, не будет периметром всего многоугольника? Это верно! Тогда у нас есть формула, которая не требует вычисления каждого треугольника, а затем умножения на количество треугольников:
Площадь правильного многоугольника = (периметр × апофема) ⁄ 2
Как рассчитать площадь любого неправильного или составного многоугольника?
Как мы видели в начале, если нам дан составной многоугольник или неправильный многоугольник, нам нужно будет искать части многоугольника, которые мы знаем, как вычислить, потому что у нас достаточно данных. сделать это.
Заключение
Как мы видели на протяжении всей этой длинной статьи, вычисление площадей заключается не только в изучении формул и их правильном применении, но также в рассуждениях и понимании того, что числа можно разделить на более простые. Иногда это будут стороны, иногда высоты, иногда диагонали…. Но скорее всего это будут треугольники. Треугольники — это простейшие многоугольники и ключевые элементы геометрии.