Расчет балки на изгиб | Блог Александра Воробьева
Опубликовано 28 Апр 2013
Рубрика: Механика | 98 комментариев
Расчет балки на изгиб «вручную», по-дедовски, позволяет познать один из важнейших, красивейших, четко математически выверенных алгоритмов науки сопротивление материалов. Использование многочисленных программ типа «ввел исходные данные…
…– получи ответ» позволяет современному инженеру сегодня работать гораздо быстрее, чем его предшественникам сто, пятьдесят и даже двадцать лет назад. Однако при таком современном подходе инженер вынужден полностью доверять авторам программы и со временем перестает «ощущать физический смысл» расчетов. Но авторы программы – это люди, а людям свойственно ошибаться. Если бы это было не так, то не было бы многочисленных патчей, релизов, «заплаток» практически к любому программному обеспечению. Поэтому, мне кажется, любой инженер должен уметь иногда «вручную» проверить результаты расчетов.
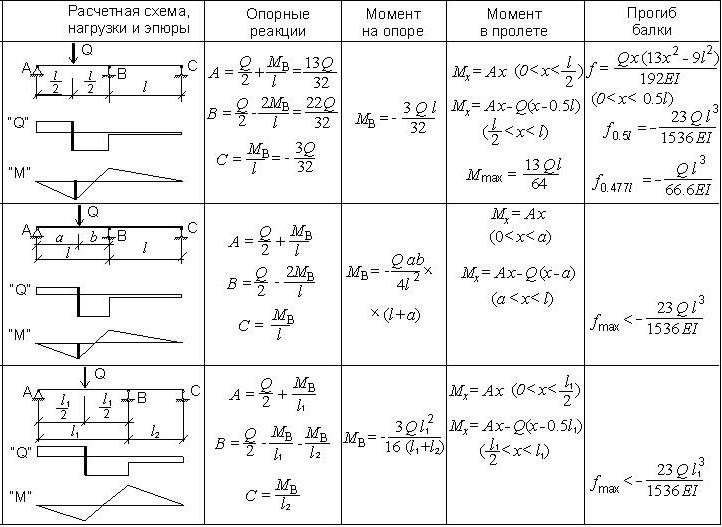
Справка (шпаргалка, памятка) для расчётов балок на изгиб представлена ниже на рисунке.
2
По прочности на изгиб расчет показал трехкратный запас прочности – турник можно смело делать из имеющегося прутка диаметром тридцать два миллиметра и длиной тысяча двести миллиметров.
Таким образом, вы теперь легко можете произвести расчет балки на изгиб «вручную» и сравнить с результатами, полученными при расчете по любой из многочисленных программ, представленных в Сети.
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Расчет балки на прогиб
вернуться в раздел РАСЧЕТЫ КМ И КЖ
Здесь представлены формулы расчета для нахождения значений изгибающих моментов и прогибов для различных балок.
| Однопролетные балки на двух шарнирных опорах | ||
| 1 | Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 2 | Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 3 | Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 4 | Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 5 | Расчет балки на двух шарнирных опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на двух опорах | ||
| 6 | Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 7 | Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 8 | Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 9 | Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 10 | Расчет балки с жестким защемлением на опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на одной опоре (консольные) | ||
| 11 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке | Смотреть расчет |
| 12 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 13 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 14 | Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента | Смотреть расчет |
| Балки двухпролетные | ||
| 15 | Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке | Смотреть |
| 16 | Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках | Смотреть |
| 17 | Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке | |
| 18 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
| 19 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
Прогиб балки: как рассчитать
Существует множество ситуаций, когда линейная направляющая или исполнительный механизм поддерживаются не полностью по всей длине.
В этих случаях прогиб (из-за собственного веса компонента и из-за приложенных нагрузок и усилий) может повлиять на ходовые качества подшипников и вызвать плохую работу в виде преждевременного износа и заедания.
Изделия, которые могут монтироваться только с концевыми опорами, такие как линейные валы или приводные узлы, или с консольной ориентацией, такие как телескопические подшипники, обычно имеют характеристики максимально допустимого отклонения. Важно проверить приложение и убедиться, что это максимальное отклонение не превышено. К счастью, большинство линейных направляющих и приводов можно смоделировать в виде балок, а их отклонение можно рассчитать с помощью обычных уравнений отклонения балки.
Соображения по материалам и конструкции
При расчете прогиба необходимо знать свойства направляющей или привода и условия приложенной нагрузки. С точки зрения направляющей или привода важными критериями являются модуль упругости и плоский момент инерции компонента.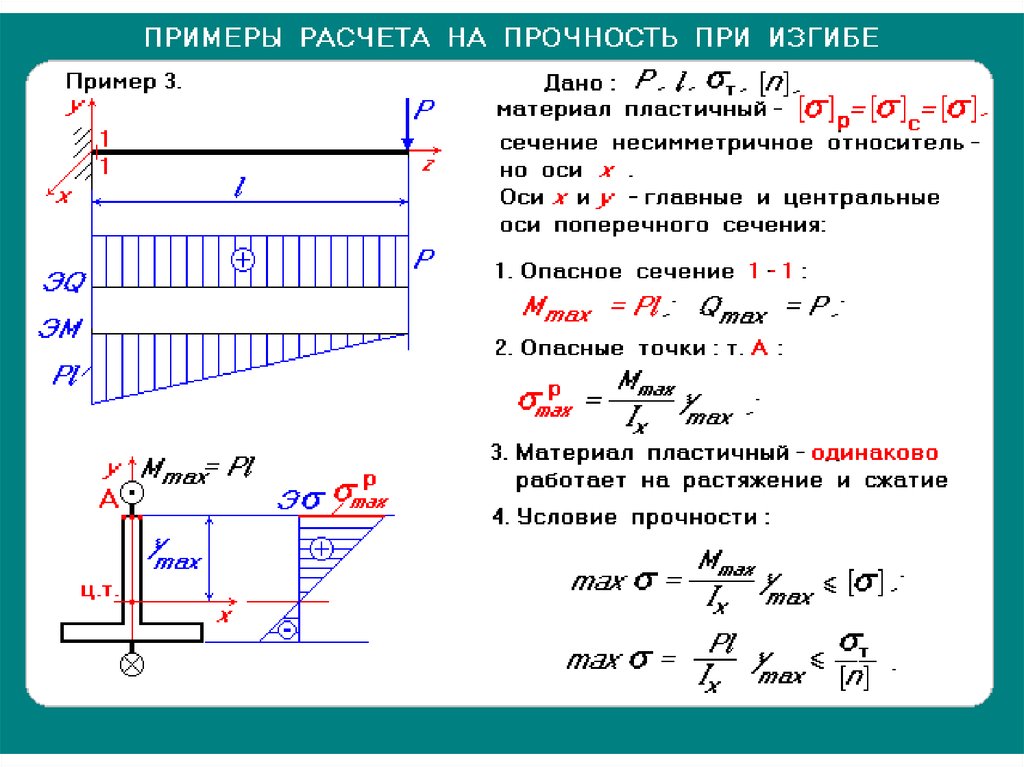
Модуль упругости является мерой жесткости материала, и обычно его можно найти в каталоге продукции. Момент инерции описывает сопротивление объекта изгибу и иногда предоставляется производителем компонента. Если момент инерции не указан, его можно разумно аппроксимировать, используя уравнение момента инерции для сплошного или полого цилиндра (для линейного круглого вала) или прямоугольника (телескопический подшипник или линейный привод).
Модуль упругости, также известный как модуль Юнга или модуль упругости при растяжении, может быть определен как отношение напряжения (силы на единицу площади) на оси к деформации (отношение деформации по длине) вдоль этой оси.
Плоский момент инерции (также называемый вторым моментом площади или моментом инерции площади) определяет, как точки площади распределяются относительно произвольной плоскости и, следовательно, ее сопротивление изгибу.
С точки зрения применения и конструкции критериями, влияющими на прогиб балки, являются тип опоры на концах направляющей или привода, приложенная нагрузка и неподдерживаемая длина.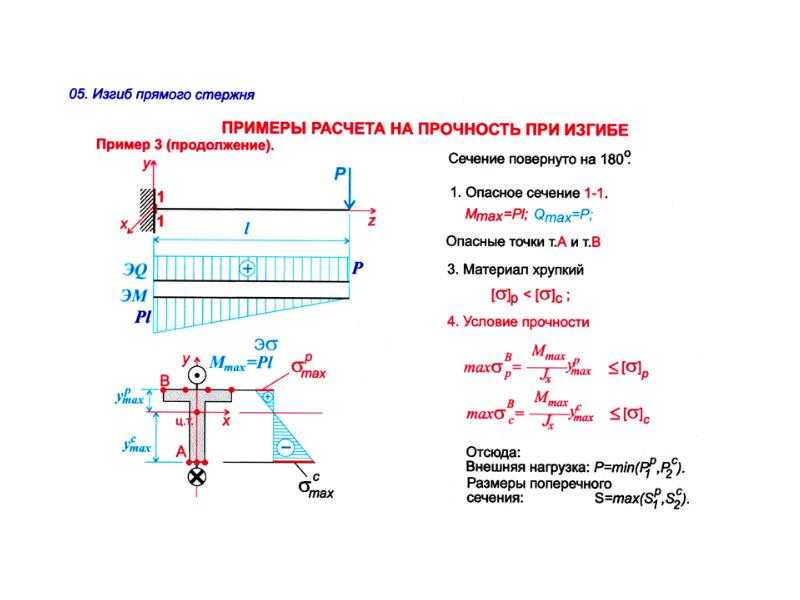
Когда компонент является консольным, его можно смоделировать как фиксированную балку, а когда он поддерживается с обоих концов, его обычно можно смоделировать как просто поддерживаемую балку. Для консольных балок максимальный прогиб будет иметь место, когда нагрузка будет находиться на свободном конце балки, а для свободно опертых балок максимальный прогиб произойдет, когда нагрузка будет находиться в центре балки.
При определении полного прогиба имейте в виду, что будут две нагрузки, вызывающие прогиб: вес самой направляющей или привода и приложенная нагрузка. Собственный вес компонента почти всегда можно смоделировать как равномерно распределенную нагрузку, а приложенную нагрузку оценить как точечную нагрузку в месте максимального прогиба (на свободном конце консольной балки или в центре свободно опертой балки). обычно обеспечивает наихудший сценарий полного отклонения.
Отклонение консольных балок
Телескопические подшипники часто бывают консольными, а некоторые конфигурации декартовых роботов приводят к консольному приводу по оси Y или Z.
В этом случае вес балки, достаточно равномерный по ее длине, вызывает максимальный прогиб на конце балки.
Это отклонение рассчитывается как:
Где:
q = усилие на единицу длины (Н/м, фунт-сила/дюйм)
L = длина без опоры (м, дюймы)
E = модуль упругости (Н/м 2 , фунт-сила/дюйм 2 )
2 )
2 )
2 ) 4 , in 4 )
Чтобы создать сценарий прогиба в наихудшем случае, мы рассматриваем приложенную нагрузку как точечную нагрузку (F) на конце балки, и результирующий прогиб можно рассчитать как:
Суммируя прогиб из-за равномерной нагрузки и прогиб из-за приложенной (точечной) нагрузки, получаем общий прогиб на конце балки:
Прогиб свободно опертых балок
Линейные валы и приводы часто закрепляются на концах, оставляя их длину неподдерживаемой, как у свободно опертой балки.
Равномерная нагрузка на балку (собственный вес вала или привода) вызовет максимальное отклонение в центре балки, которое можно рассчитать как:
моделируется как точечная нагрузка в центре балки для наихудшего сценария.
Изображение предоставлено: wikipedia.orgПрогиб из-за приложенной нагрузки в этом состоянии рассчитывается как:
Общий прогиб в центре балки:
Прогиб валов с двумя подшипниками
7 При использовании двух подшипников на свободно опертой балке, как это обычно бывает с направляющими круглого вала, приложенная нагрузка распределяется между двумя подшипниками, и максимальный прогиб происходит в двух местах: в месте
каждый подшипник , когда узел подшипника (иногда называемый кареткой или столом) находится в середине вала. Изображение предоставлено: Thomson LinearРасчет прогиба балки для этого условия:
Опять же, мы должны добавить прогиб из-за собственного веса балки плюс прогиб из-за приложенной нагрузки, чтобы получить общий прогиб из:
Существуют дополнительные сценарии монтажа и нагрузки, которые могут встречаться в некоторых приложениях, например, в приводе с фиксированной опорой на обоих концах.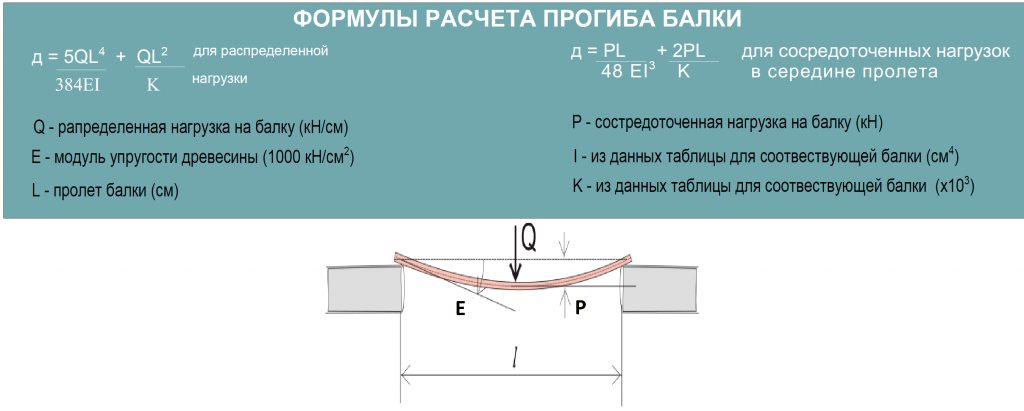
Но, как и в приведенных выше примерах, их можно оценить с помощью стандартных уравнений отклонения балки. Полный список сценариев поддержки балки и уравнений прогиба см. на этой странице Корнельского университета.
Источник изображения: wikipedia.org
Калькуляторы прогиба балки — EngineerExcel
Расчет прогиба балки применим к нескольким сценариям проектирования конструкций. Например, расчет отклонения консольной балки может определить силы, действующие на крыло самолета.
Калькуляторы прогиба балки
Самый простой способ определить прогиб балки под действием силы или момента — использовать калькулятор и параметры балочной системы. В зависимости от балочной системы, консольной, просто поддерживаемой или неподвижно-фиксированной, были оценены различные случаи, чтобы получить уравнение для расчета отклонения балки как функции расстояния вдоль балки.
Калькуляторы прогиба консольной балки
Существует пять общих случаев для учета прогиба консольной балки.
Консольная балка с конечным усилием
Первый – это прогиб под действием силы на свободном конце балки, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
где:
- F сила, приложенная к концу балки (Н)
- х — позиция вдоль балки, где оценивается прогиб (м)
- E — модуль Юнга материала балки (Па)
- I – момент инерции площади (м4)
- L общая длина балки (м)
Консольная балка с нагрузкой в любой точке
Второе отклонение консольной балки — это отклонение из-за силы, приложенной в какой-либо точке, отличной от конца, как показано ниже:
Прогиб балки можно рассчитать с помощью следующих уравнений:
где a — расстояние от поддерживаемого конца до места действия силы (м).
Консольная балка с равномерно распределенной нагрузкой
Третье отклонение консольной балки представляет собой отклонение из-за силы, приложенной равномерно по длине балки, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
где w равномерная нагрузка (Н/м).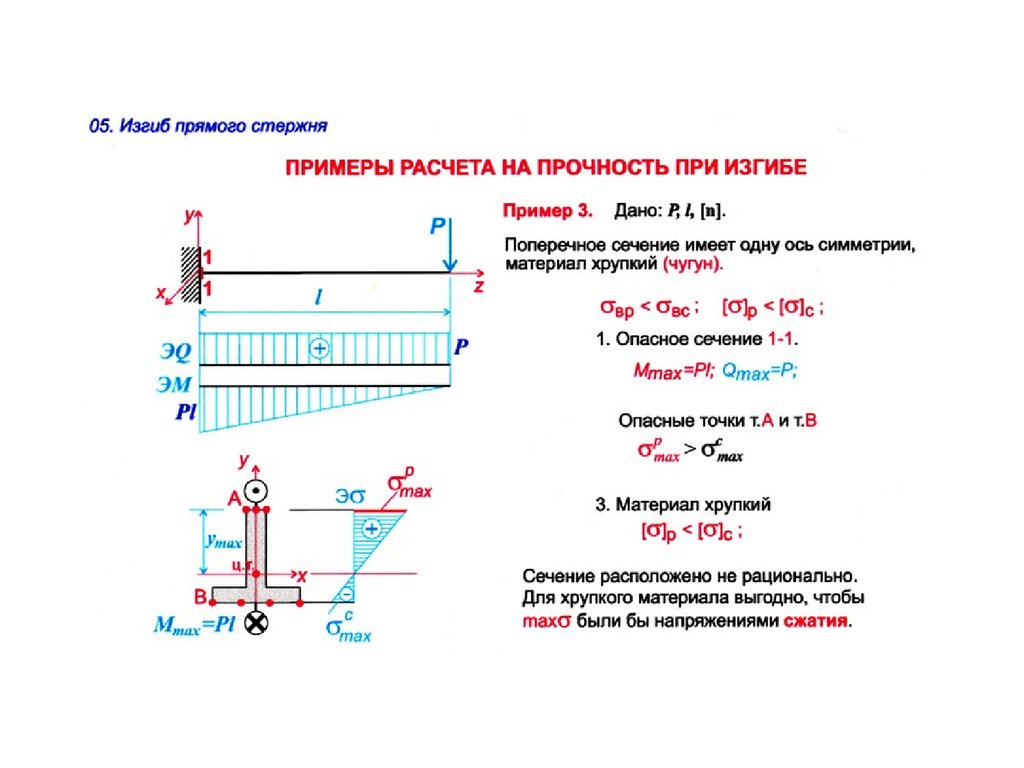
Консольная балка с треугольной распределенной нагрузкой
Четвертое отклонение консольной балки представляет собой отклонение из-за треугольной распределенной силы, приложенной по длине балки, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения :
где w 1 — максимальное значение силы (Н).
Консольная балка с конечным моментом
Конечным прогибом консольной балки является прогиб из-за момента на свободном конце балки, как показано ниже:
Прогиб балки можно рассчитать по следующему уравнению:
где M 0 — момент, приложенный к свободному концу (Н∙м).
Калькуляторы прогиба свободно опертой балки
Просто опертая балка с нагрузкой в любой точке
Существует семь общих случаев для рассмотрения прогиба свободно опертой балки. Первый – это отклонение из-за промежуточной силы, как показано ниже:
Отклонение балки можно рассчитать с помощью следующего уравнения:
, где a и b — расстояния по обе стороны от приложенной силы (м).
Свободно опертая балка с нагрузкой в середине пролета
Второй прогиб свободно опертой балки — это прогиб из-за силы, приложенной к центру балки, как показано ниже:
Прогиб балки можно рассчитать с помощью Следующее уравнение:
Свободно опертая балка с равномерно распределенной нагрузкой
Третье отклонение свободно опертой балки — это отклонение из-за равномерно распределенной силы, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
Свободно опертая балка с моментом на каждом конце
Четвертый прогиб свободно опертой балки представляет собой прогиб из-за моментов на обеих опорах, как показано ниже:
прогиб можно рассчитать по следующему уравнению:
Свободно опертая балка с моментом на одном конце
Пятый прогиб свободно опертой балки — это прогиб из-за момента на одной опоре, как показано ниже:
Прогиб балки можно рассчитать по следующему уравнению:
Свободно опертая балка с моментом в центре
Окончательный прогиб свободно опертой балки — это прогиб из-за момента в центре балки, как показано ниже :
Прогиб балки можно рассчитать по следующему уравнению:
Калькуляторы отклонения фиксированной-фиксированной балки
Фиксированная-фиксированная балка с нагрузкой в середине пролета
Существуют два общих случая для рассмотрения фиксированной-фиксированной отклонение луча.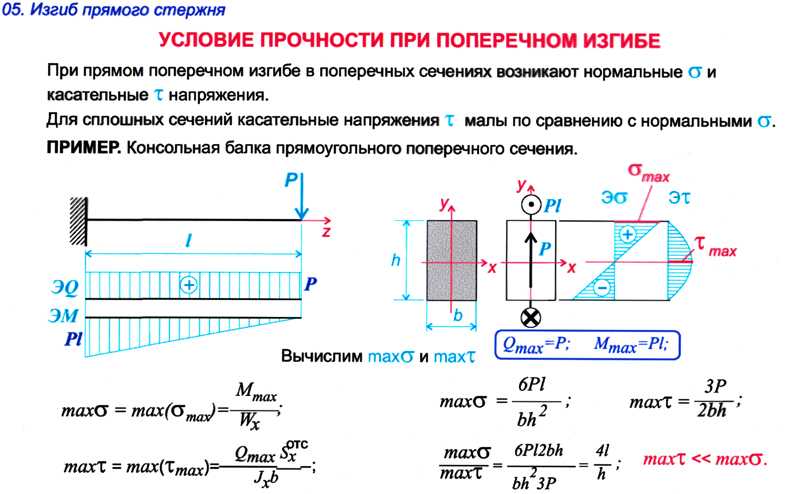
Первый — это отклонение из-за силы в центре, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
Неподвижно-неподвижная балка с равномерно распределенной нагрузкой
Другое фиксированно-неподвижное отклонение балки представляет собой отклонение из-за равномерно распределенной силы, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
Дифференциальный расчет прогиба балки
Другой метод расчета прогиба балки включает использование дифференциального уравнения кривой прогиба для оценки поведения балки при изгибе. Здесь представлен обзор этого метода, однако конкретные детали выходят за рамки этого введения.
В этом методе используется общее уравнение, и его можно применять к любой комбинации сил и моментов, действующих в любой точке балки. Используемое уравнение:
где:
- v — прогиб балки (м)
- d 2 v/dx 2 — вторая производная прогиба относительно положения вдоль балки
- M — изгибающий момент вдоль балки в зависимости от положения (Н∙м)
Изгибающий момент в каждой секции балки рассчитывается как функция x .