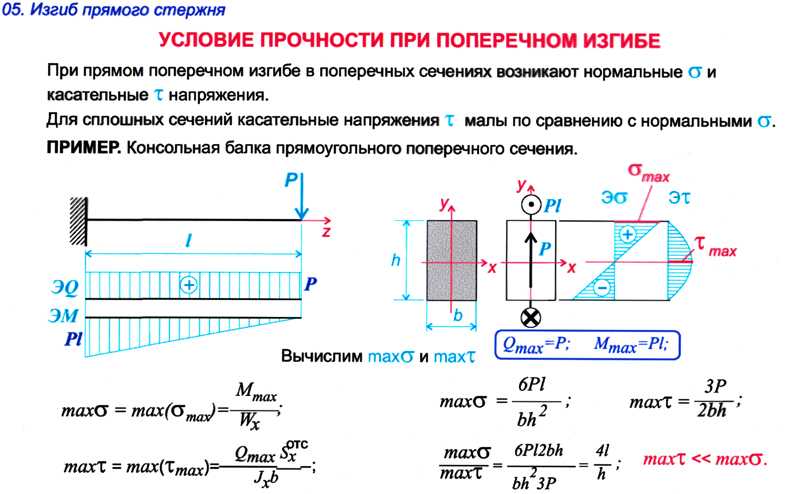
- Онлайн-калькулятор для расчета деревянных балок перекрытия
- Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность. • AST3D
- (Отклонение — TotalConstructionHelp)
- , для этих Например, было использовано значение 119000. Если используется сталь, то значение E будет около 2
- 00, как показано в примерах. Момент инерции (I) будет либо рассчитан, либо выбран из таблиц. предоставлено или вычислено. (См. раздел «Расчет момента инерции») Допустимый прогиб: опорные полы и потолки L/360, опорные Крыши с уклоном менее 3 из 12 L/240 и несущие крыши больше чем 3 в 12 наклон L/180. L = пролеты, например: 12 футов, умножить 12 футов на 12 дюймов = 144 дюйма, разделенных на 360, 240 или 180, в зависимости от того, что применимо. Наконец, сравните расчетное отклонение с допустимым отклонением. Если Расчетное отклонение больше, чем допустимое отклонение, то вы должны выберите элемент балки большего размера и выполните повторный расчет. Простая балка с сосредоточенной нагрузкой на опорной точке с уравнениями и решениями: Как рассчитать размеры деревянных балок
Онлайн-калькулятор для расчета деревянных балок перекрытия
Skip to content
Рубрика: Черновая отделка
Хотите разместить рекламу ваших товаров или услуг на сайте cdelayremont.ru? Перейдите на страницу реклама, чтобы узнать о вариантах и условиях сотрудничества.
Одним из самых популярных решений при устройстве межэтажных перекрытий в частных домах является использование несущей конструкции из деревянных балок. Она должна выдерживать расчетные нагрузки, не изгибаясь и, тем более, не разрушаясь. Прежде чем приступить к возведению перекрытия рекомендуем воспользоваться нашим онлайн-калькулятором и рассчитать основные параметры балочной конструкции.
Высота балки (мм):
Ширина балки (мм):
Материал древесины:
СоснаЕльЛиственница
Пролет (м):
Шаг балок (м):
Коэффициент надежности:
1,11,21,31,41,51,61,71,81,92,0
- Высота и ширина определяют площадь сечения и механическую прочность балки.

- Материал древесины: сосна, ель или лиственница – характеризует прочность балок, их стойкость к прогибам и излому, другие особые эксплуатационные свойства. Обычно отдают предпочтение сосновым балкам. Изделия из лиственницы применяют для помещений с влажной средой (бань, саун и т.п.), а балки из ели используют при строительстве недорогих дачных домов.
- Сорт древесины влияет на качество балок (по мере увеличения сорта качество ухудшается).
- 1 сорт. На каждом однометровом участке бруса с любой стороны могут быть здоровые сучки размером 1/4 ширины (пластевые и ребровые), размером 1/3 ширины (кромочные). Могут быть и загнившие сучки, но их количество не должно превышать половины здоровых. Также нужно учитывать, что суммарные размеры всех сучков на участке в 0,2 м должны быть меньше предельного размера по ширине. Последнее касается всех сортов, когда речь идет о несущей балочной конструкции. Возможно наличие пластевых трещин размером 1/4 ширины (1/6, если они выходят на торец).

- 2 сорт. Такой брус может иметь здоровые сучки размером 1/3 ширины(пластевые и ребровые), размером 1/2 ширины (кромочные). По загнившим сучкам требования, как и для 1 сорта. Материал может иметь глубокие трещины длиной 1/3 длины бруса. Максимальная длина сквозных трещин не должна превышать 200 мм, могут быть трещины на торцах размером до 1/3 от ширины. Допускается: наклон волокон, крень, 4 кармашка на 1 м., прорость (не более 1/10 по длине или 1/5 – по толщине или ширине), рак (протяжением до 1/5 от длины, но не больше 1 м).

- 3 сорт. Тут допуски по порокам больше: брус может иметь сучки размером 1/2 ширины. Пластевые трещины могут достигать 1/2 длины пиломатериала, допускаются торцевые трещины размером 1/2 от ширины. Для 3 сорта допускается наклон волокон, крень, кармашки, сердцевина и двойная сердцевинаы, прорость (не более 1/10 по длине или 1/4 — по толщине или ширине), 1/3 длины может быть поражена раком, грибком, но гнили не допускаются. Максимальное количество червоточин — 3 шт. на метр. Обобщая: 3 сорт даже невооруженным глазом выделяется не самым лучшим качеством. Но это не делает его непригодным для изготовления перекрытий по балкам.Подробнее про сорта читайте ГОСТ 8486-86 Пиломатериалы хвойных пород. Технические условия;
- 1 сорт. На каждом однометровом участке бруса с любой стороны могут быть здоровые сучки размером 1/4 ширины (пластевые и ребровые), размером 1/3 ширины (кромочные). Могут быть и загнившие сучки, но их количество не должно превышать половины здоровых. Также нужно учитывать, что суммарные размеры всех сучков на участке в 0,2 м должны быть меньше предельного размера по ширине. Последнее касается всех сортов, когда речь идет о несущей балочной конструкции. Возможно наличие пластевых трещин размером 1/4 ширины (1/6, если они выходят на торец).
- Пролет – расстояние между стенами, поперек которых укладываются балки.

- Шаг балок определяет частоту их укладки и во многом влияет на жесткость перекрытия;
- Коэффициент надежности вводится для обеспечения гарантированного запаса прочности перекрытия. Чем он больше, тем выше запас прочности
Наш онлайн-калькулятор позволит вам рассчитать параметры деревянных балок и подобрать оптимальную конфигурацию перекрытия.
4
Понравилась статья? Поделиться с друзьями:
Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность. • AST3D
Skip to content
 Главная › Инфо › Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность.
При проектировании и изготовлении конструкций из металла и других материалов очень важно соблюдать и выполнять физико-механические расчеты на прочность, одним из которых является расчет балок на изгиб (прогиб). Выполнять расчет прогиба балки онлайн — очень удобно и быстро. Поэтому специалисты нашего предприятия подготовили онлайн калькулятор для расчетов.
Выполнять расчет прогиба балки онлайн — очень удобно и быстро. Поэтому специалисты нашего предприятия подготовили онлайн калькулятор для расчетов.
Расчет прогиба балки онлайн
Профиль
Материал
СтальЧугунАлюминийДеревоФанераМедьФторопластАкрилПоликарбонат
Способ фиксации
Шарнир-Шарнир (распределенная) Шарнир-Шарнир (точечная) Заделка-Шарнир (распределенная) Заделка-Шарнир (точечная) Заделка-Заделка (распределенная) Заделка-Заделка (точечная) Свободный конец (распределенная) Свободный конец (точечная)Схема фиксации
Значения
Выберите профиль
Результаты расчетов
Площадь поперечного сечения профиля:
—
Расчетный вес профиля (балки):
—
Прогиб балки F
—
Описание
При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр». Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.
Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Сделать расчет вала ЧПУ на прогиб также можно произвести на данном калькуляторе. Следовательно Вы будете знать предварительные прочностные показатели перед сборкой ЧПУ станка.
Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)
Ключевые слова: расчет балки на прогиб, расчет балки на прочность, расчет балки на двух опорах, расчет балки на изгиб, расчет балки онлайн бесплатно, расчет балки перекрытия, расчет балки на прогиб пример, расчет балки онлайн, расчет прогиба деревянной балки, расчет прогиба балки, расчет прогиба профильной трубы онлайн, расчет прогиба балки на двух опорах, расчет прогиба плиты перекрытия, расчет прогиба швеллера, beam deflection calculator, free, calculator online, Free Online Beam Calculator, Elastic beam deflection calculator, расчет прогиба металлической балки, расчет прогиба листа, расчет прогиба фанеры, расчет на прочность онлайн, расчет на прочность при изгибе, расчет на прогиб деревянной балки, расчет на прогиб металлической балки, расчет на прогиб, расчет на прогиб уголка
Редакция AST3D 17. 09.2018 11:11
09.2018 11:11
(Отклонение — TotalConstructionHelp)
(Отклонение — TotalConstructionHelp)(Здесь мы будем обращаться к конструкционным балкам, лагам и перемычкам, а не к искусственным Балки)
| Балки и перемычки на самом деле просто балки. Балка – это конструктивный элемент, обычно располагаемый горизонтально и способный
выдерживать нагрузки, в первую очередь за счет сопротивления изгибу. Изгибающая сила
индуцированных в материале балки в результате нагрузок, включающих ее
собственный вес (вес балки) и дополнительные нагрузки (другие нагрузки, называемые динамическими нагрузками).
и неподвижные грузы, такие как люди и мебель). Эти нагрузки производят то, что
называются изгибающими моментами в балке, а также могут иметь изгибающие моменты в каждой
поддерживаемый конец, когда концы закреплены на торцевых опорах. Балки бывают разных размеров и форм. Они, как правило, либо однородны или композитный. Однородный пучок — это пучок из одного материала, например, дерево или сталь. Композит – это материал, изготовленный из разных материалов, таких как как, бетонная балка со стальной арматурой. Некоторые типы балок: |
| Все это может показаться чрезмерным, но это не так.  Некоторые эксперты говорят, что инженерия состоит на 80% из логики и на 20% из приложений. Некоторые могут обсудить это. но здесь мы предоставим вам основную инженерную информацию и приложения, которые вы не всегда можете найти доступными. Пока балки нагружены по-разному. Свободно опертая балка представляет собой обычно используемый луч (как показано выше). Ниже вам будет показано, как все это работает и как выбрать балку (деревянную или сталь). Мы также коснемся выбора бетонной балки в разделе Балка. Простая опорная равномерно распределенная балка с уравнениями и решениями:В приведенном выше примере есть шаги, необходимые для выбора и проектирования дерева. Луч. Если вы хотите выбрать и спроектировать стальную балку, шаги будут такими: такой же. Есть несколько вещей, которые меняются, например, напряжение на изгиб в Материал, момент инерции, модуль упругости и сечение Модуль.  Обычные этапы проектирования балки:
Простая балка с сосредоточенной нагрузкой на опорной точке с уравнениями и решениями: |
Как рассчитать размеры деревянных балок
Последнее обновление: 8 ноября 2022 г.
После того, как мы рассмотрели все необходимые основы, мы наконец можем определить размеры деревянной балки. Если вы не читали посты о Статических системах деревянных крыш, Нагрузках и Комбинациях нагрузок, я рекомендую вам взглянуть, прежде чем начать читать этот пост в блоге.
Во-первых: Что мы имеем в виду, когда размер или размер балки ?
Для расчета размеров/размеров деревянных балок необходимо выполнить расчеты как ULS (предельное состояние), так и SLS (предельное состояние эксплуатационной пригодности).
В конструкции ULS размеры деревянной балки определяются по предельным напряжениям изгиба и сдвига деревянного материала. В конструкции SLS деревянная балка проверяется на предмет непревышения предела прогиба.
Я знаю, что все это звучит довольно сложно🤔 но не волнуйтесь, мы объясним это практически на примерах и картинках. Позвольте мне объяснить вам шаги, которые мы должны сделать, чтобы измерить балку.
Давайте посмотрим на шаги, которые нам нужно выполнить. Вы можете увидеть их визуально на следующем рисунке.
- Выберите статическую систему, например, свободно опертую балку
- Рассчитайте все типичные нагрузки (постоянные, снеговые, ветровые, динамические нагрузки и т. д.)
- Рассчитайте все комбинации нагрузок
- Выберите древесный материал и найдите свойства материала ($k_{mod}$, $f_{c.0.k}$, $f_{m.k}$, $\gamma_{M}$)
- Примем ширину w и высоту h поперечного сечения
- Проверьте балку на изгиб. Если не проверено, увеличьте ширину или высоту балки и повторите расчет
- Проверьте балку на сдвиг.
 Если не проверено, увеличьте ширину или высоту балки и повторите расчет
Если не проверено, увеличьте ширину или высоту балки и повторите расчет - Проверьте балку на соответствие критерию мгновенного отклонения. Если не проверено, увеличьте ширину или высоту балки и повторите расчет.
- Проверьте балку на соответствие окончательным критериям прогиба. Если не проверено, увеличьте ширину или высоту балки и повторите расчет
- Если все эти проверки выполнены, значит, вы определили правильные размеры балки.
Мы рассмотрим свободно опертую балку, которая используется в плоской крыше.
Статическая система свободно опертой балки может быть визуализирована, как показано на следующем рисунке. Он состоит из одного ролика (воспринимает вертикальную силу V2) и одной шарнирной опоры (воспринимает вертикальную V1 и горизонтальную силу h2).
Статическая система | Просто поддерживаемая балка. Чтобы сохранить контекст, эта свободно опертая балка может быть второстепенной балкой в плоской крыше.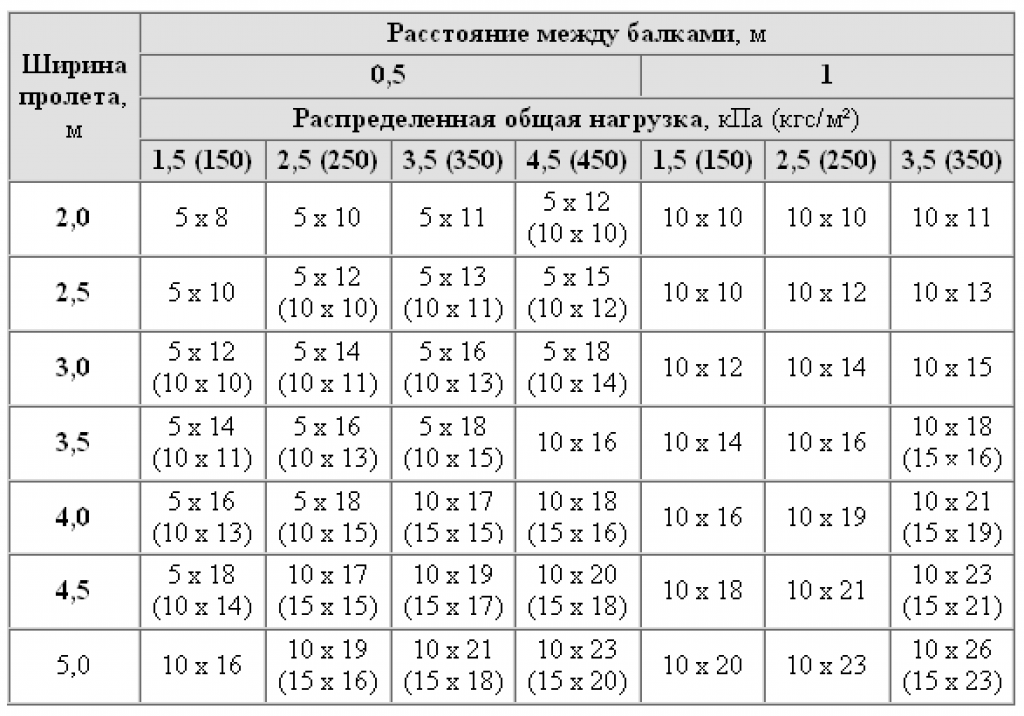
Теперь, когда мы визуализируем второстепенные балки (пунктирные на рисунке) в 2D разрезе, мы можем легко сравнить их со статической системой.
Статическая система второстепенных балокВ этом посте вы можете узнать больше о различных типах деревянных крыш и о том, как работают их статические системы.
Нагрузки
Мы будем использовать нагрузки, которые мы предполагали в нашем блоге о сочетаниях нагрузок. Если вы хотите узнать больше о различных типах нагрузок, что они собой представляют и как их применять, вы можете прочитать это в этом посте.
| . | Характерная стоимость живой нагрузки | ||
| $ s_ {k} $ | 1,0 кН/м2 | Характеристическая стоимость снежной нагрузки | |
| $ W_ {K} $ | -1,0292023 3 | 92023 92023 920232 | 32 | .
Материал балки
Во-первых, проектировщику необходимо выбрать между конструкционной древесиной и инженерной древесиной, такой как Glulam (клееный брус) или LVL (ламинированный шпон).
Выбор дизайнера зависит от проекта, пролетов, стоимости и личного вкуса.
Итак, для нашего примера балки мы используем конструкционную древесину C24.
Теперь нам нужно найти свойства этой древесины, и мы можем найти их либо в Еврокоде, либо найти производителя в Интернете, у которого есть таблицы его изделий из древесины. 92}$
Коэффициент модификации $k_{mod}$
Коэффициент модификации $k_{mod}$ учитывает влияние влажности и продолжительности нагрузки на свойства древесины .
Этот коэффициент будет использоваться для расчета расчетных напряжений в деревянных элементах.
Содержание влаги делится на 3 категории или так называемые классы обслуживания.
Эти классы эксплуатации показывают, насколько деревянный элемент подвергается воздействию влаги, а это означает, что элемент, подвергающийся воздействию дождя, может быть отнесен к классу эксплуатации 3, а элемент внутри здания может быть отнесен к классу эксплуатации 1.
Подробное описание можно найти в EN 1995-1-1 2.3.1.3.
Классы длительности нагрузки показывают, как долго нагрузка действует на конструкцию, поскольку чем дольше нагрузка, тем сильнее ухудшаются свойства древесины.
Статическая нагрузка, например, действует на конструкцию постоянно, в то время как ветровая нагрузка действует только в течение короткого времени и поэтому может быть классифицирована как мгновенная нагрузка.
Классы продолжительности нагрузки приведены в таблице 2.2 стандарта EN 1995-1-1.
Теперь в нашем случае мы предполагаем, что проектируем плоскую крышу жилого дома. Балки не подвержены влиянию погодных условий. Поэтому у нас есть Класс обслуживания 1 .
Кроме того, мы также можем определить продолжительность нагрузок, действующих на нашу плоскую крышу, в соответствии с таблицей 2.2 стандарта EN 1995-1-1.
| Собственная/собственная нагрузка | Постоянная |
| Временная нагрузка, снеговая нагрузка | Среднесрочная |
| Ветровая нагрузка | Мгновенная |
Теперь мы можем найти значения $k_{mod}$ для конструкционной древесины C24 (массивная древесина) и наших различных нагрузок согласно EN 1995-1-1 Таблица 3.1
| $k_{mod}$ | |||
|---|---|---|---|
| Self-weight/dead load | Permanent action | Service class 1 | 0.6 |
| Live load, Snow load | Medium term действие | Сервисный класс 1 | 0,8 |
| Ветровая нагрузка | Мгновенное действие | Класс 1 | 1,1 |
ПАРТИКА
. в УЛС. EN 1995-1-1 Таблица 2.3 представляет рекомендуемые частные коэффициенты.
в УЛС. EN 1995-1-1 Таблица 2.3 представляет рекомендуемые частные коэффициенты.
В нашем случае для массивной древесины мы получаем частный коэффициент
$\gamma_{M} = 1,3$
Допущение ширины и высоты балки
Прежде чем мы наконец сможем приступить к проектированию балки, нам нужно определить ширину и высоту поперечного сечения балки. Это основано на опыте дизайнера.
Ознакомьтесь с этой статьей, чтобы оцифровать свои ручные вычисления.
Ширина w = 80 мм
Высота h = 240 мм
Зная высоту и ширину поперечного сечения, мы можем рассчитать момент инерции прочной оси, необходимый для рассчитать напряжение из-за изгиба. 92} * 0,8 м $
Теперь эти линейные нагрузки можно применить к нашей статической системе. В качестве примера применим нагрузку LC1.
Изгиб Из 3 основных комбинаций нагрузок LC1, LC3 и LC5 мы можем рассчитать наиболее критический изгибающий момент. 2}{8}$ 94} * \frac{0,24m}{2} $
2}{8}$ 94} * \frac{0,24m}{2} $
Последний шаг, прежде чем мы сможем проверить, может ли поперечное сечение выдержать нагрузки, — это расчет напряжения сопротивления древесины. материал.
$ f_{m.d} = k_{mod} * \frac{f_{m.k}}{\gamma_{m}} $
| LC1 (P-действие) | $k_{mod.P} * \frac{f_{m.k}}{\gamma_{m}} $ | $0,6 * \frac{24 МПа}{1,3} $ | $11,1 МПа $ |
| LC3 (L-действие) | $k_{mod.L} * \frac{f_{m.k}}{\gamma_{m}} $ | $0,8 * \frac{24 МПа}{1,3} $ | $14,77 МПа $ |
| LC5 (I-действие) | $k_{mod.I} * \frac{f_{m.k}}{\gamma_{m}} $ | $1,1 * \frac{24 МПа}{1,3} $ | $20,31 МПа $ |
Наконец, мы можем рассчитать использование поперечного сечения в его наиболее критической точке.
$\eta = \frac{\sigma}{f_{m.d}}$
| LC1 (P-действие) | $\frac{\sigma. P}{f_{m.d.P}} $ P}{f_{m.d.P}} $ | $\frac{4,76 МПа}{11,1 МПа} $ | $ 0,43 $ |
| LC3 (L-действие) | $ \frac{\sigma.L}{f_{m.d.L}} $ | $\frac{13 МПа}{14,77 МПа} $ | $ 0,88 $ |
| LC5 (I-действие) | $\frac{ \sigma.I}{f_{m.d.I}} $ | $\frac{10,1 МПа}{20,31 МПа} $ | $ 0,5 $ |
LC1, LC3 и LC5 мы можем продолжить и рассчитать наиболее критическую силу сдвига. Самая высокая сила сдвига в свободно опертая балка находится рядом с двумя опорами и может быть рассчитана по следующей формуле:
$V_{d} = q * \frac{L}{2}$
приложенная нагрузка на балку
Это приводит к следующим силам сдвига из-за LC1, LC3 и LC5
| LC1 (P-действие) | $1,17 \frac{kN}{ м} * \frac{5m}{2} $ | $ 2,93 кН $ |
| LC3 (L-образное действие) | $3,2 \frac{кН}{м} * \frac{5м}{2} $ | $8 кН $ |
| LC5 (I-действие) | $2,48 \frac{кН}{м} * \frac {5 м}{2} $ | $ 6,2 кН $ |
По поперечным силам можно рассчитать напряжение в наиболее критическом поперечном сечении (около опоры свободно опертой балки).
$\tau = \frac{3}{2} * \frac{V_{d}}{w * h} $
| LC1 (P-действие) | $\frac{3}{2 } * \frac{2,93 кН}{0,08 м * 0,24 м} $ | $0,23 МПа $ |
| LC3 (L-действие) | $\frac{3}{2} * \frac{8 кН}{0,08м * 0,24м} $ | $0,63 МПа $ |
Последний шаг, прежде чем мы сможем проверить выдерживает ли поперечное сечение нагрузки, рассчитывается сопротивление сдвигу деревянного материала.
$f_{v.d} = k_{mod} * \frac{f_{v.k}}{\gamma_{m}}$
| LC1 (P-действие) | $k_{mod.P} * \frac{f_{v.k}}{\gamma_{m}} $ | $0,6 * \frac{4 МПа}{1,3} $ | $1,85 МПа $ |
| LC3 (L-действие) | $k_{mod.L} * \frac{f_{v.k}}{\gamma_{m}} $ | $0,8 * \frac{4 МПа}{1,3} $ | $2,46 МПа $ |
| LC5 (I-действие) | $k_{mod. I} * \frac{f_{v.k}}{\gamma_{m}} $ I} * \frac{f_{v.k}}{\gamma_{m}} $ | $1,1 * \frac{4 МПа}{1,3} $ | $3,39 МПа $ |
Наконец, мы можем рассчитать использование поперечного сечения в его наиболее критической точке.
$\eta = \frac{\tau}{f_{v.d.}}$
| LC1 (P-действие) | $\frac{\tau.P}{f_{v.d.P}} $ | $\frac{0,23 МПа}{1,85 МПа} $ | $ 0,124 $ |
| LC3 (L-действие) | $\frac{\tau.L}{f_{v.d.L}} $ | $\frac {0,63 МПа}{2,46 МПа} $ | $ 0,25 $ |
| LC5 (I-действие) | $\frac{\tau.I}{f_{v.d.I}} $ | $\frac{0,48 МПа}{3,39 МПа} $ | $ 0,14 $ |
EN 1995-1-1 Таблица 7. 2 рекомендует значения для $w_{inst}, w_{net.fin}$ и $w_{fin}$, которые не должны превышаться для свободно опертой балки .
2 рекомендует значения для $w_{inst}, w_{net.fin}$ и $w_{fin}$, которые не должны превышаться для свободно опертой балки .
| $w_{inst}$ | $w_{net.fin}$ | $w_{fin}$ | ||||
| $L/300$ до $L/500$ | 3 | 3 | 3 | 3 | $w_{fin}$ $ до $L/350 $ | $L/150$ до $L/300 $ |
При длине балки (пролете) L=5м мы получаем следующие значения.
| $w_{inst}$ | $w_{net.fin}$ | $w_{fin}$ |
| 16.67mm to 10mm | 20mm to 14.3mm | 33.3mm to 16.67mm |
$u_{inst}$ (мгновенная деформация) нашей балки может быть рассчитана с нагрузкой характерного сочетания нагрузок. Глядя на все комбинации нагрузок, мы видим, что LC3 приводит к наибольшей нагрузке, где временная нагрузка является ведущей, а снеговая нагрузка является сопутствующим переменным действием.



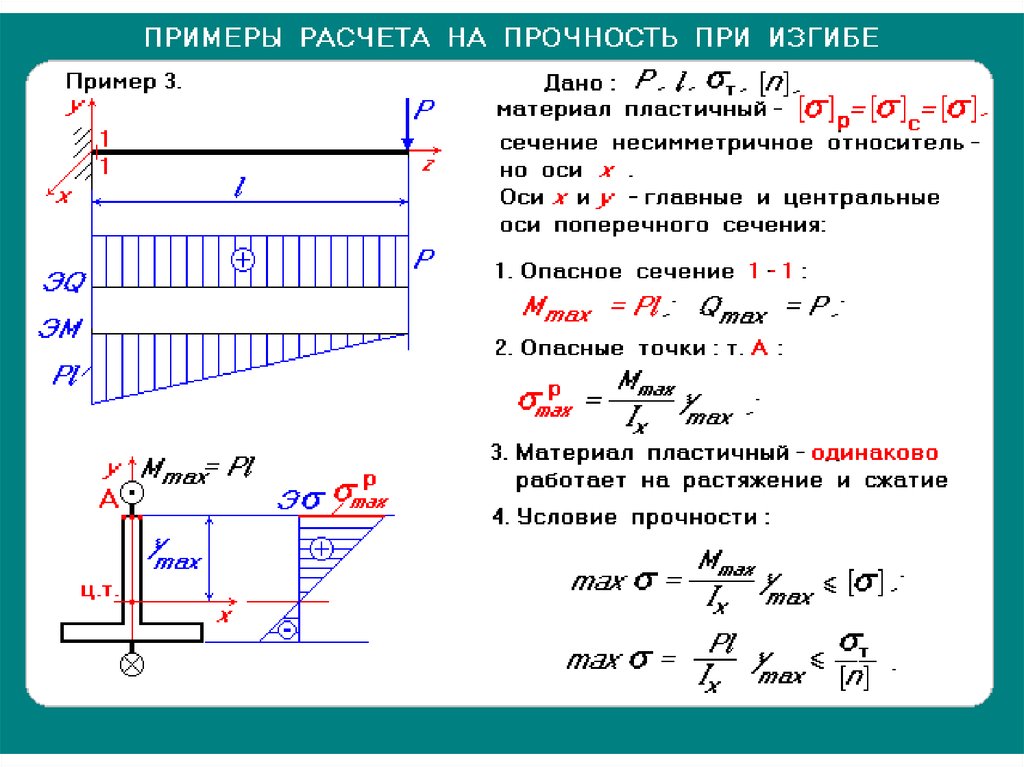
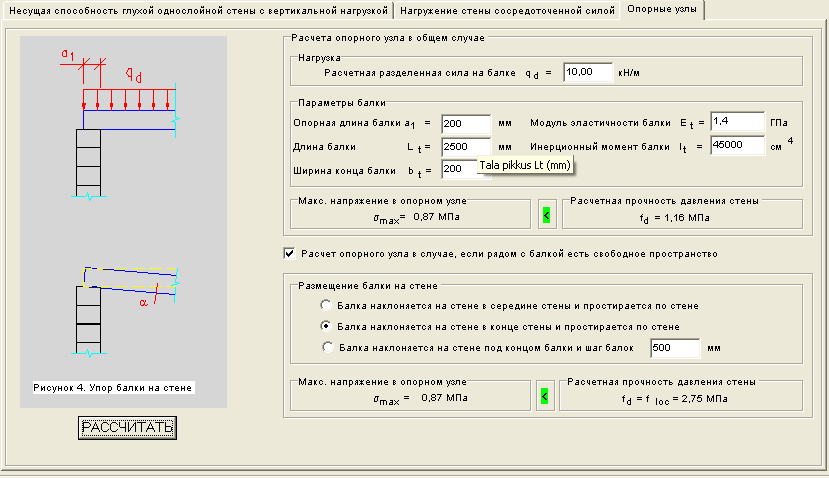 Мы хотим, чтобы Beam
быть разработан для максимальной безопасности. Для свободно опертой балки с
Равномерно распределенная нагрузка M = WL 2 /8.
Мы хотим, чтобы Beam
быть разработан для максимальной безопасности. Для свободно опертой балки с
Равномерно распределенная нагрузка M = WL 2 /8. Так
если у вас ограниченное пространство, стальная балка может быть лучшим выбором.
Так
если у вас ограниченное пространство, стальная балка может быть лучшим выбором. В примере максимальное отклонение
разрешено контролируется Кодексом. Различные допустимые отклонения показаны на
пример. Чтобы вычислить отклонение, нам нужна дополнительная информация,
который равен E (модулю упругости) материала и I (моменту упругости).
Инерция) для выбранного элемента. (См. раздел «Расчет момента инерции»).
на этом веб-сайте)
В примере максимальное отклонение
разрешено контролируется Кодексом. Различные допустимые отклонения показаны на
пример. Чтобы вычислить отклонение, нам нужна дополнительная информация,
который равен E (модулю упругости) материала и I (моменту упругости).
Инерция) для выбранного элемента. (См. раздел «Расчет момента инерции»).
на этом веб-сайте)