- Калькулятор деревянной двутавровой балки
- Расчёт металлической балки онлайн (калькулятор).
- | Calcresource
- Калькулятор консольной балки
- Теоретические основы
- Введение
- Консольная балка с равномерно распределенной нагрузкой
- Консольная балка с точечной силой на конце
- Консольная балка с сосредоточенной силой в произвольном положении
- Консольная балка с точечным моментом
- Консольная балка с переменной распределенной нагрузкой
- Распределение нагрузки трапециевидной формы на консольной балке является типичным 9
- Консольная балка с частично распределенной равномерной нагрузкой
- Contilever Beam с частично распределенной Trapezoid Load Wrate Wrate Wrate Wrate Wrate Wrate Wordile. линейно изменяющаяся величина от w_1 до w_2, а оставшаяся длина разгружается. Размеры w_1 и w_2 являются силой на длину. Общая сила, приложенная к балке, равна W={L-a-b\over2}(w_1+w_2), где L — длина балки, а a, b — ненагруженные длины левой и правой сторон балки соответственно.
- Статьи по теме
- Новый калькулятор свободного луча SkyCiv
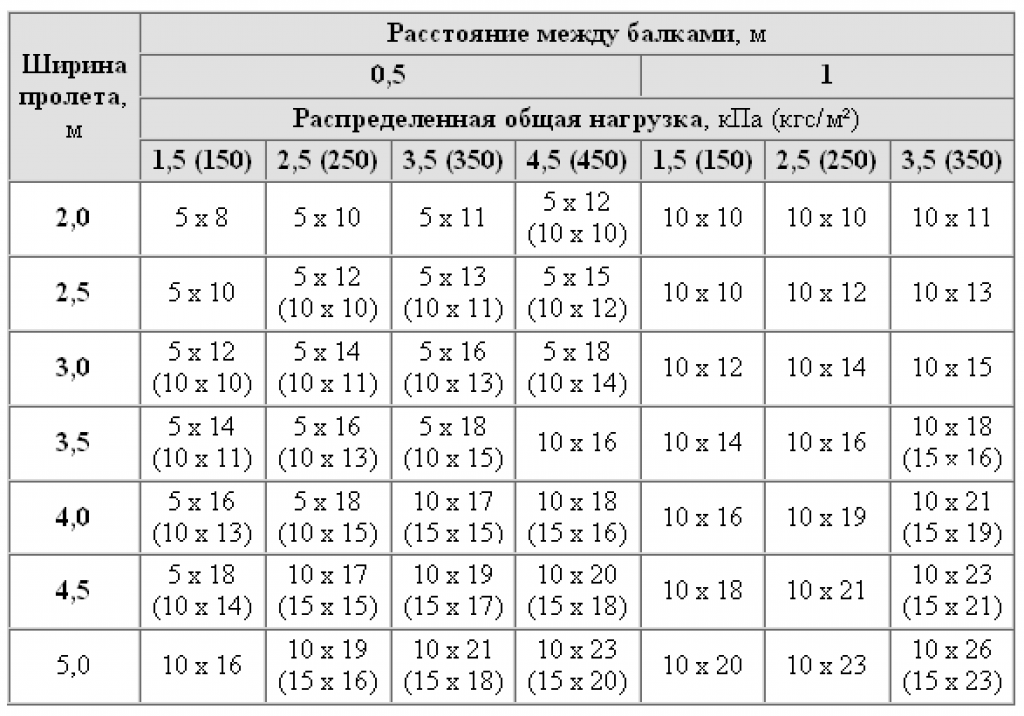
Калькулятор деревянной двутавровой балки
Нормативные документы
Проектирование и расчёт любых деревянных конструкций регламентируется специальными документами, сводами норм, правил и техническими кодексами. За всё время существования строительной отрасли их существует великое множество, и разобраться в них, порой, очень не просто. Некоторые нормы заменяются новыми, некоторые отменяются совсем, вводятся новые требования, поправки, дополнения и т.д. В основе этого калькулятора лежит документ СНБ 5.05.01-2000 «»Деревянные конструкции», однако, на данный момент в Беларуси действует другой документ: ТКП 45-5.05-275-2012 «Деревянные конструкции. Правила расчёта». В этом документе имеется раздел «Указания по проектированию балок», в котором, в свою очередь, записано: «Расчет клеефанерных балок по предельным состояниям несущей способности необходимо выполнять в соответствии с ТКП EN 1995-1-1 Проектирование деревянных констркуций. Общие правила». Последний документ (Технический Кодекс устоявшейся Практики) уже полностью идентичен европейскому стандарту EN 1996-5:2008 Eurocode 5: Design of timber structures — Part 1-1, на что указывают буковки EN в названии документа (введён в РБ в 2009 году). Тем не менее, калькулятор написан на основе СНБ 5.05.01-2000! Тому есть парочка причин.
Тем не менее, калькулятор написан на основе СНБ 5.05.01-2000! Тому есть парочка причин.
Во-первых, действующий ТКП подразумевает разделение пиломатериала по 18 классам прочности!!! Я попробовал обратиться в лесхоз с вопросом продажи мне доски класса С40. Думаю, вы без труда догадаетесь, какой ответ я получил =) Не смотря на то, что эта лесопилка была государственная, и не самая маленькая в области они не могут обеспечить нормальную сортировку даже по трём сортам, не говоря уже о 18 классах, для сортировки по которым требуется обязательное наличие лаборатории, проверяющей чуть-ли не каждую доску на разрыв, сжатие, смятие и т.д. В общем, на практике лесхозы пользуются ГОСТом от 80-го года и в ближайшем будущем купить доску класса С40 или D70 просто невозможно.
Во-вторых, действующий КТП активно ссылается на другие европейские документы, в частности по клеям, которые в бесплатном варианте недоступны никак, я искал (это интеллектуальная собственность разработчиков) и этот нюанс накладывает ограничение на получение некоторых исходных данных для расчётов.
В-третьих, я просто не смог до конца разобраться в хитростях новых формул, а они отличаются… Кроме того, эти два документа (КТП 45-5.05.275.2012 и КТП EN 1995-1-1) ссылаясь друг на друга имеют разные данные (например, в одном из них 4 класса длительности воздействия нагрузки, а в другом 5; в одном 5 классов эксплуатации — а в другом 3, отличаются так же и коэффициенты модификации, частные коэффициенты материалов и т.д.)
Действующий КТП всё-же не прошёл совсем уж мимо. Из него был взят коэффициент прочности системы, который позволяет учитывать распределение нагрузок в случае наличия соответствующих связей между балками. Так же калькулятор рассчитывает равновесную влажность древесины исходя из температуры и влажности воздуха, и назначает соответствующий класс эксплуатации по ТКП 45-5.05-275-2012.
Кроме уже упомянутых ТНПА использован СНиП 2.01.07-85 «Нагрузки и воздействия», из которого взяты стандартные величины нагрузок, снеговые и ветровые нагрузки, а так-же все возможные коэффициенты, связанные с определением величин нагрузок.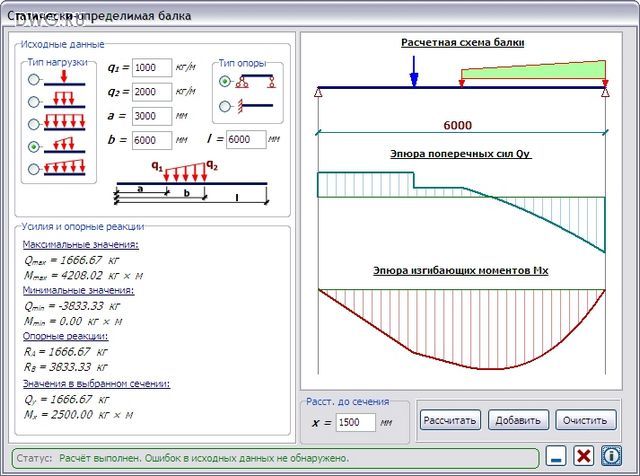
С 12,01,2021 flash не поддерживается по умолчанию.
Вот способ от одного из подписчиков:
Шаг1. Удалить с компа все версии флэшплеера, у Adobe есть на сайте прога для этого.
Шаг 2. Скачать и установить флэшплеер версии 27 или ниже.
Метод работает в браузере Яндекс. Говорят, что ещё на Мозиле работает. Правда, в Хроме не работает всё равно.
Расчёт металлической балки онлайн (калькулятор).
Калькулятор предусматривает расчёт балок на изгиб и прогиб, из горячекатаного и другого проката следующей номенклатуры:
- уголка равнополочного;
- уголка неравнополочного;
- швеллера с уклоном и с параллельными гранями полок;
- двутавров с уклоном полок и с параллел. гранями полок различных модификаций, а также тавровых балок (тавров).
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и 8510-86; швеллеров — 8240-97; двутавров — 26020-83; тавров — ТУ 14-2-685-86; (получаемых продольным разрезом пополам горячекатаных двутавров с парал-ыми гранями полок по ГОСТ 26020-83) — смотрите калькулятор веса двутавра.
При вычислении массы 1 метра длины проката плотность стали в этих стандартах принята равной 7,85 г/см3 (7.85 кг/дм3 или 7850кг/м3).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке «РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ»; размеры полок уголков в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
Швеллер в наличии на складе в Москве
Швеллер является продукцией прокатного производства, которая имеет U-образное поперечное сечение. В зависимости от технологии производства, швеллеры бывают горячекатаные и гнутые.
Размеры и форма г/к швеллеров общего назначения регламентируются стандартом ГОСТ 8240-97. Ширина проката согласно указанному нормативному документу может быть от 32 до 115 мм, а высота 50 — 400 мм.
В обозначении номера профиля зашифрована высота швеллера в сантиметрах (цифра) и серия или тип профиля (буква).
Размеры гнутого швеллера регламентируются стандартом ГОСТ 8278-83.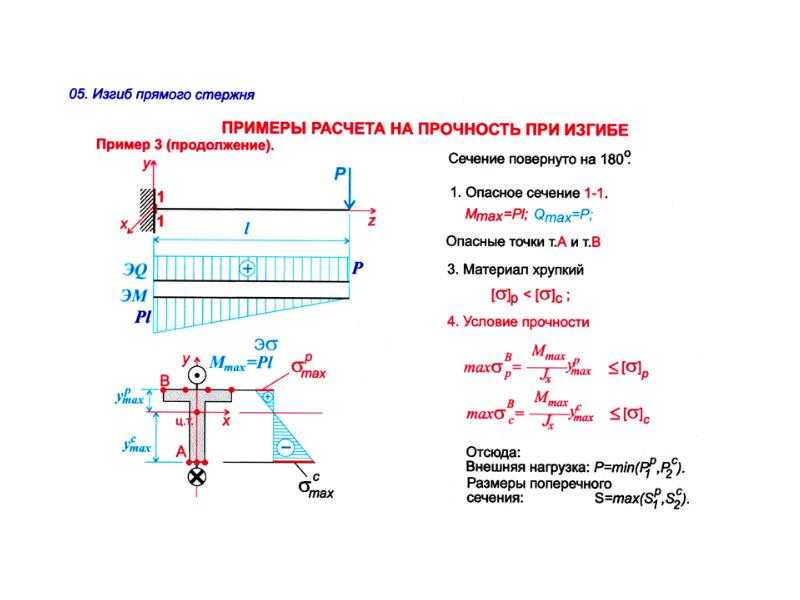 В соответствии этому документу высота профиля может принимать значение от 25 до 410 мм, толщина швеллера — от 2 до 8 мм, и ширина может быть 26 — 160 мм.
В соответствии этому документу высота профиля может принимать значение от 25 до 410 мм, толщина швеллера — от 2 до 8 мм, и ширина может быть 26 — 160 мм.
В APEX L вы сможете приобрести швеллер наиболее востребованных размеров из стали марок Ст3 и 09Г2С:
- серии П с параллельными гранями — типоразмеры профиля 5П — 30П;
- серии У с уклоном граней — типоразмеры профиля 6,5У — 30У;
- гнутый швеллер с размерами от 50х40х3 до 250х125х6.
Значения высоты и ширины полки, ширины и толщины стенки по ГОСТ 8240-97 смотрите на странице — Как правильно расшифровать условное обозначение швеллера.
Виды перекрытий
По назначению перекрытия можно разделить на:
- цокольные — отделяют первый этаж здания от цокольного этажа или подвала
- межэтажные — направлены на разделение между собой этажей здания
- чердачные. Первые . Из названия второго вида следует, что они . Последние отделяют чердачное помещение от жилого здания.
В зависимости от конструктивных особенностей перекрытия их можно разделить на плиточные и балочные:
- Плиточные перекрытия чаще всего монтируют в крупногабаритных каменных домах с использованием железобетонных плит.
- Балочные перекрытия используются при строительстве малоэтажных жилых домов. Для их монтажа могут применяться металлические или деревянные балки.
Основные способы усиления швеллера
Можно встретить различные ситуации, когда необходимо провести мероприятия по усилению той или иной конструкции, выполненной из швеллера или другого вида проката. Существует множество различных способов, которые можно применить для усиления швеллера. Среди них можно выделить несколько типовых ситуаций.
Существует множество различных способов, которые можно применить для усиления швеллера. Среди них можно выделить несколько типовых ситуаций.
1. На этапе проектирования можно подобрать швеллер большего размера; изготовленный из более прочной марки стали. Если же размеры балки по высоте строго или частично ограничены, то можно использовать швеллер усиленный (серия С горячекатаных швеллеров, которая при совпадающих номерах профиля, обладает большими значениями площади и моментов сопротивления/инерции), составное сечение балки/стержня, которое можно выполнить из двух швеллеров, либо швеллер+полоса/уголок и т.д.
2. В случае, если необходимо усилить уже существующую конструкцию, то можно провести следующие мероприятия. 1) Увеличение сечения швеллера, которое можно осуществить приваркой полосы, уголка, швеллера либо к полкам, либо к стенкам, и этим самым, либо изменить площадь и сопротивление сечения, либо снизить нагрузку, воспринимаемую одним швеллером. 2) Организацией дополнительных распорок, связей ребер, диафрагм с целью увеличения местной или общей устойчивости швеллера и конструкции. 3) Монтаж дополнительных элементов, которые изменяют схему конструкции (шпренгельные элементы, подкосы и т.д.). 4) Бетонирование конструкции — позволяет повысить жесткость и несущую способность колонн и стоек из швеллера и прочего проката.
3) Монтаж дополнительных элементов, которые изменяют схему конструкции (шпренгельные элементы, подкосы и т.д.). 4) Бетонирование конструкции — позволяет повысить жесткость и несущую способность колонн и стоек из швеллера и прочего проката.
3. В случае, если элемент конструкции находится в предаварийном состоянии, то усиливать его не стоит, а следует произвести замену.
Конструктивные особенности
Швеллеры 2 вида:
- П-образного сечения прокат горячекатаный;
- П-образного сечения прокат гнутый.
Конструктивное исполнение швеллера с 2 полками в 1 сторону располагает главную ось инерции к стенке со смещением усилий, накладываемых к изделию. Оно работает на косой изгиб. Лёгким и прочным каркас из швеллера получится, когда швеллер модернизировать. Сделать из него коробчатые стойки. Электрической дуговой сваркой с прерывистым швом соединить швеллеры полками внутрь конструкции. Усиление шва через 1,2-1,5 м упрочняет сборное изделие.
Балке из двутавра не требуется дополнительное усиление. Она выдерживает нагрузки.
Она выдерживает нагрузки.
| Calcresource
Прыжки до
-калькулятор
-Теоретический фон
Соглашение о таблице
-Калькулятор
-Теоретический фон
-Введение
-Запуск
-Соглашение. с равномерной распределенной нагрузкой
— Консольная балка с точечным усилием на конце
— Консольная балка с точечным усилием в произвольном положении
— Консольная балка с точечным моментом
— Консольная балка с переменной распределенной нагрузкой
— Консольная балка с плитным трапециевидным распределением нагрузки
— Консольная балка с частично распределенной равномерной нагрузкой
— Консольная балка с частично распределенной трапециевидной нагрузкой
– Статьи по теме
Поделитесь этим
См. также
также
Калькулятор консольной балки
— Автор: д-р Минас Э. Лемонис, доктор наук. Обновлено: 27 июня 2020 г.
Главная > Статика > Консольная балка
Этот инструмент рассчитывает статическую реакцию консольных балок при различных сценариях нагрузки. Инструмент рассчитывает и строит диаграммы для следующих величин:
- реакции
- изгибающие моменты
- поперечные силы сдвига
- прогибы
- уклоны
Пожалуйста, имейте в виду, что приняты предположения теории балок Эйлера-Бернуля. является упругим, а поперечное сечение постоянным на всем пролете балки (призматическая балка).
- Вместо этого переходите к теории и формулам!
Units: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Структура | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L = | mcmmmydftin | 94|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассчитайте момент инерции балок различных сечений с помощью наших специальных калькуляторов. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ADVERTISEMENT |
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Imposed loading: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Uniform distributed loadUniform распр. нагрузка (суммарная)Точечная нагрузка на остриеТочечная нагрузкаТочечный моментТреугольная нагрузкаТрапециевидная нагрузкаТрапециевидная нагрузка (плита)Частичная равномерная нагрузкаЧастичная треугольная нагрузкаЧастичная трапециевидная нагрузка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Calculate | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Results: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reactions: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R A = | kNNkgtlbfkip | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M A = | kNmNmkg. mt.mlbf.ftlbf.inkip.ftkip.in mt.mlbf.ftlbf.inkip.ftkip.in | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
МОМЕНТ СОЗДАНИЯ: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M U = | KNMNMKG.MT.MLBF.FTLBF.INKIP.FTKIP.INMNMKG.MT.MLBF.FTLBF.INKIP.FTKIP.INMNMKG.MT.MLBF.FTLBF.INKIP.FTKIP.INMNMKG.MT.MLBF.FTLBF.INKIP.INMNMKG.MT.MLBF.FTLBF.INKIP.INMNMKG.MT.MLBF.FTLBF.INKIP.INMNMKG. | MCMMMMYDFTIN | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Поперечный сдвиг0003 | mcmmmydftin | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Deflection: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d u = | mcmmmydftin | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x d = | mcmmmydftin | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Уклоны: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ A = | Degradmrad | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ B = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ B = 9003 | θ B = | θ B = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ B = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ0076 | degradmrad | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Request results at a specific point: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X = | MCMMMYDFTIN | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M (x) = | KNMNMKG. MT.MLBF.IINCL.IINCL.INICHP.INICHP.IINCL.INKP.ININK.INCK.INK.INK.INK.INK.INK.0076 MT.MLBF.IINCL.IINCL.INICHP.INICHP.IINCL.INKP.ININK.INCK.INK.INK.INK.INK.INK.0076 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
V(x) = | kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d(x) = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ(x) = | degradmrad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diagrams | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| degradmrad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kN/mN/mkg/mt/mlbf/ftlbf/inkip/ft | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ADVERTISEMENT
Top Pages
Поделиться
Теоретические основы
Содержание
— Введение
— Допущения
— Условные знаки
— Условные обозначения
— Консольная балка с равномерно распределенной нагрузкой
— Консольная балка с точечным усилием на вершине
— Консольная балка с точечным усилием в произвольном положении
— Консольная балка с точечным моментом
— Консольная балка с переменной распределенной нагрузкой
— Консольная балка с трапециевидной плитой распределение нагрузки
— Консольная балка с частично распределенной равномерной нагрузкой
— Консольная балка с частично распределенной трапециевидной нагрузкой
— Связанные статьи
Введение
Консольная балка является одной из самых простых конструкций. Он имеет только одну опору на одном из концов. Опора представляет собой так называемую фиксированную опору , которая препятствует любому перемещению, включая вертикальные или горизонтальные смещения, а также любые повороты. Другой конец не поддерживается, поэтому он может свободно перемещаться или вращаться. Этот свободный конец часто называют наконечником кантилевера.
Он имеет только одну опору на одном из концов. Опора представляет собой так называемую фиксированную опору , которая препятствует любому перемещению, включая вертикальные или горизонтальные смещения, а также любые повороты. Другой конец не поддерживается, поэтому он может свободно перемещаться или вращаться. Этот свободный конец часто называют наконечником кантилевера.
Удаление единственной опоры или вставка внутреннего шарнира превратили бы консольную балку в механизм: тело движется без ограничений в одном или нескольких направлениях. Это нежелательная ситуация для несущей конструкции. В результате консольная балка не имеет избыточности в плане опор. Если произойдет локальный отказ, вся конструкция рухнет. Эти типы структур, которые не предлагают избыточности, называются критическими или детерминантными структурами. Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется 9. 0557 избыточная или неопределенная структура. Консольная балка является определяющей конструкцией.
0557 избыточная или неопределенная структура. Консольная балка является определяющей конструкцией.
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Как правило, для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M. Для консольной балки, которая воспринимает только поперечные нагрузки, осевая сила всегда равна нулю. , при условии, что прогибы малы. Поэтому довольно часто пренебрегают осевыми силами.
Результаты расчетов на этой странице основаны на следующих допущениях:
- Материал однородный и изотропный (другими словами, его характеристики одинаковы во всех точках и в любом направлении)
- Материал линейно-упругий
- Нагрузки приложены статически (не меняются со временем)
- Поперечное сечение одинаково по всей длине балки
- Прогибы небольшие
- Каждое поперечное сечение, изначально плоское, а также нормальное к продольной ось, остается плоской и нормальной к отклоненной оси.
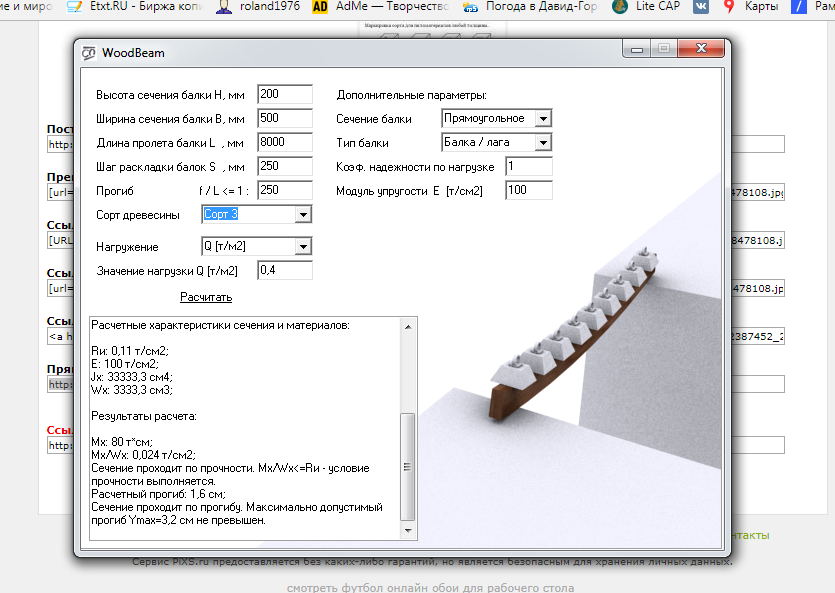 Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение).
Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение).
Последние два предположения удовлетворяют кинематическим требованиям теории балки Эйлера-Бернулли, которая также принимается здесь.
Правила знаков
Для расчета внутренних сил и моментов в любом сечении балки необходимо соблюдать правила знаков. Здесь приняты следующие значения:
- Осевая сила считается положительной, если она вызывает растяжение детали.
- Сила сдвига положительна, когда она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила хоть и не обязательны, но достаточно универсальны. Другой набор правил, если им следовать последовательно, также приведет к тем же физическим результатам.
Условные обозначения положительного знака для внутренней осевой силы, Н, поперечной силы, В, и изгибающего момента, МСимволы
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общая длина балки
- R: опорная реакция
- d: прогиб
- M: изгибающий момент
- V: поперечный сдвиг усилие
- \тета: уклон
Консольная балка с равномерно распределенной нагрузкой
Нагрузка w распределена по всему консольному пролету, имея постоянную величину и направление. Его размеры представляют собой силу на длину. Суммарная сила, приложенная к консольной балке, равна W=w L, где L — длина балки. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 92)}{6 E I}
Его размеры представляют собой силу на длину. Суммарная сила, приложенная к консольной балке, равна W=w L, где L — длина балки. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 92)}{6 E I}
Консольная балка с точечной силой на конце
Сила сосредоточена в одной точке, расположенной на свободном конце балки. Однако на практике сила может быть распределена по небольшой площади, хотя размеры этой области должны быть существенно меньше длины кантилевера. В непосредственной близости от приложения силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление. По мере того, как мы удаляемся от места действия силы, результаты становятся достоверными в силу принципа Сен-Венана.
В следующей таблице приведены формулы, описывающие статическую реакцию консольной балки на сосредоточенную точечную силу P, приложенную к концу. 2}{2EI} 92(3L-x)}{6EI}
2}{2EI} 92(3L-x)}{6EI}
Консольная балка с сосредоточенной силой в произвольном положении
Сила сосредоточена в одной точке в любом месте по длине кантилевера. Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.
Следующая таблица содержит формулы, описывающие статическую реакцию консольной балки на сосредоточенную точечную силу P, приложенную на произвольном расстоянии a от неподвижной опоры.
Cantilever beam with point load at random position | |
|---|---|
| Quantity | Formula |
| Reactions: | R_A=P M_A=-Pa |
End slopes : 92(3x — a)\over 6EI} &, x>a\end{выровнено} \right.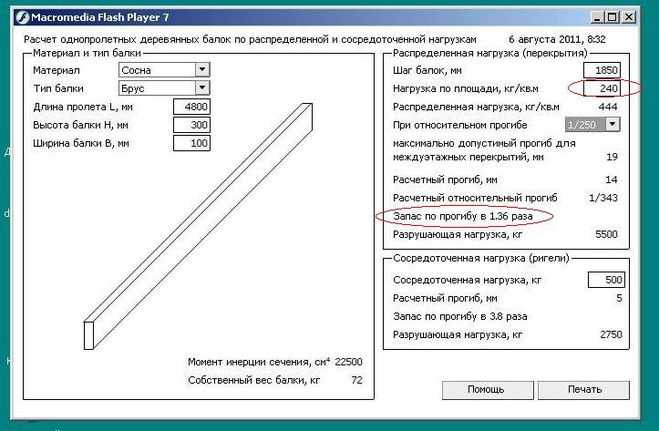 | |
| Наклон в точке x: | \theta(x)=\left\{\begin{align} -& {Px(2a — x)\over 2EI} &, x\le a \\& \theta_B & , x>a\end{выровнено} \right. |
Консольная балка с точечным моментом
В этом случае момент создается в одной точке балки в любом месте по пролету. С практической точки зрения это может быть пара сил или элемент при кручении, соединенный вне плоскости и перпендикулярно балке.
В любом случае область приложения момента должна распространяться на небольшую длину кантилевера, чтобы его можно было успешно идеализировать как сосредоточенный момент в точке. Несмотря на то, что в непосредственной близости от области применения результаты, предсказанные классической теорией балки, как ожидается, будут неточными (из-за концентрации напряжений и других локализованных эффектов), предсказанные результаты становятся полностью достоверными, когда мы удаляемся, как заявил Святой — Принцип Венана.
Следующая таблица содержит формулы, описывающие статическую реакцию консольной балки на сосредоточенный точечный момент M, приложенный на расстоянии a от неподвижной опоры.
Cantilever beam with point moment | |
|---|---|
| Quantity | Formula |
| Reactions: | R_A=0 M_A=M |
| End slopes: | \theta_A =0 \theta_B =\frac{M a}{ E I } |
| Предельный изгибающий момент: | M_u=M |
| Предельная сила сдвига: | _u=|
| Наклон в точке x: | \theta(x)=\left\{\begin{align}& \frac{M x}{E I} &, x\le a \\& \theta_B &, x> a\end{выровнено} \right. |
Консольная балка с переменной распределенной нагрузкой
Нагрузка распределяется по всей длине консоли с линейно изменяющейся величиной, начиная от w_1 на неподвижной опоре до w_2 на свободном конце. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L — длина кантилевера.
Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L — длина кантилевера.
Если w_1=0, формулы в следующей таблице соответствуют треугольной распределенной нагрузке с возрастающей величиной (пик на вершине).
Если w_2=0, формулы в следующей таблице соответствуют треугольной распределенной нагрузке с уменьшающейся величиной (пик на неподвижной опоре).
В следующей таблице приведены формулы, описывающие статическую реакцию консольной балки трапециевидной формы на переменную распределенную нагрузку.
где: w_x=w_1+{(w_2-w_1)\over L}x |
Распределение нагрузки трапециевидной формы на консольной балке является типичным 9
для консольных балок, поддерживающих плиту. Распределение имеет вид прямой трапеции с возрастающей частью вблизи неподвижной опоры и постоянной частью с величиной, равной w, на оставшейся длине до вершины. Размеры w представляют собой силу на длину.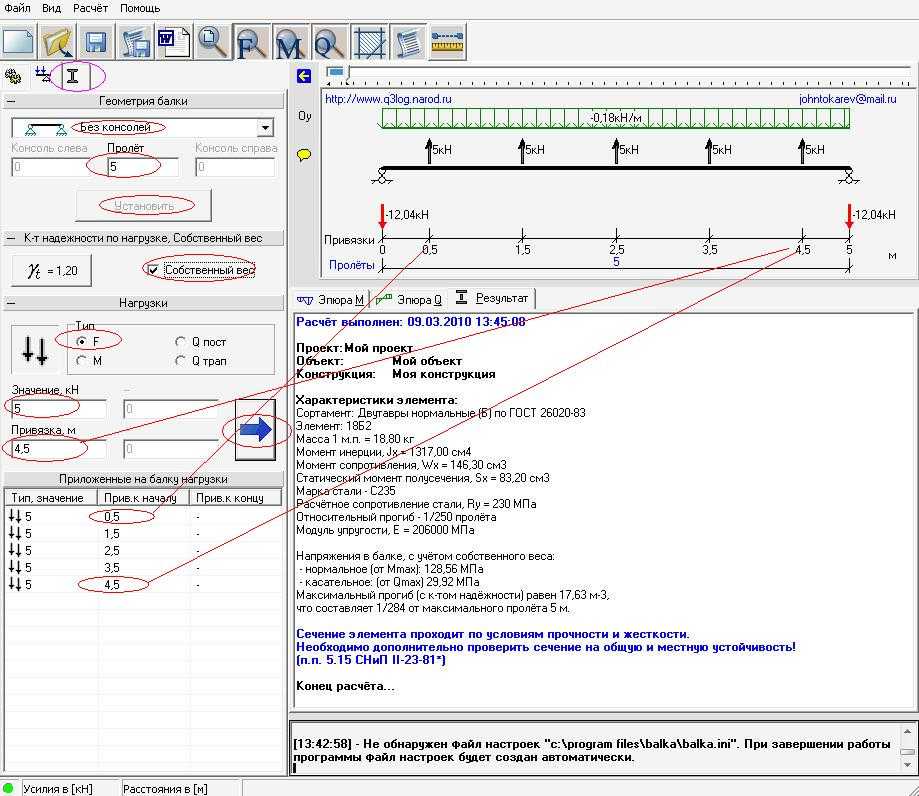 2\right) 93}{6EI} &,x> a \end{align}\right.
2\right) 93}{6EI} &,x> a \end{align}\right.Консольная балка с частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть длины консоли с постоянной величиной w, а остальная часть не нагружена. Размеры w представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w\left(L-a-b\right), где L — длина консоли, а a, b — ненагруженные длины левой и правой сторон балки соответственно.
Следующая таблица содержит формулы, описывающие статическую реакцию консольной балки на частично распределенную равномерную нагрузку.
Cantilever beam with partially distributed uniform load | |
|---|---|
| Quantity | Formula |
| Reactions: | R_A=wL_w M_A=- wL_w\left(a+{L_w\over 2}\справа) |
| Концевые откосы: | 93}{6EI}&, a{<}x{<}L-b\\ &\theta_B &,x\ge L-b \end{выровнено}\right.|
Где: x_a = x-a L_W = L-A-B L_B = L-B | |
Contilever Beam с частично распределенной Trapezoid Load Wrate Wrate Wrate Wrate Wrate Wrate Wordile. линейно изменяющаяся величина от w_1 до w_2, а оставшаяся длина разгружается. Размеры w_1 и w_2 являются силой на длину. Общая сила, приложенная к балке, равна W={L-a-b\over2}(w_1+w_2), где L — длина балки, а a, b — ненагруженные длины левой и правой сторон балки соответственно.
Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок могут быть получены путем соответствующей установки значений w_1 и w_2. Кроме того, соответствующие случаи для полностью загруженного пролета могут быть получены путем установки a и b равными нулю.
Следующая таблица содержит формулы, описывающие статическую реакцию консольной балки на частично распределенную трапециевидную нагрузку.
Балка консольная с частично распределенной линейно-переменной нагрузкой (трапециевидная) 93}{24EI}&, a{<}x{<}L-b\\ &\theta_B &,x\ge L-b \end{выровнено}\right. | |
|---|---|
Где: x_a = x-a L_W = L-A-B L_1 = L+A-B L_B = L-B 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 3 9000 2 9000 2 9000 2 |
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
См. также
Новый калькулятор свободного луча SkyCiv
15.02.2023
SkyCiv — поставщик облачного программного обеспечения для проектирования конструкций и API-технологий. Бесплатный калькулятор балок компании — один из самых популярных бесплатных ресурсов среди студентов и профессионалов в области проектирования строительных конструкций. Это веб-инструмент, который позволяет пользователям выполнять структурный анализ и проектные расчеты для простых и консольных балок.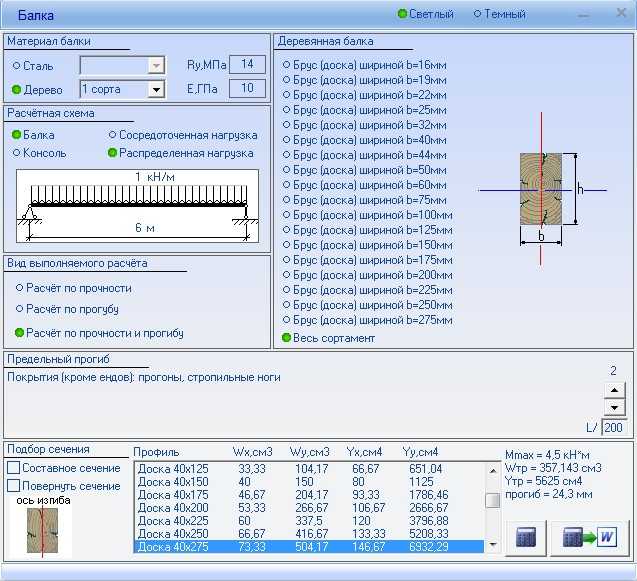 Бесплатный инструмент рассчитывает изгибающие моменты, силы сдвига, прогибы и реакции для заданной геометрии балки и условий нагрузки, помогая студентам и профессиональным инженерам проектировать безопасные и эффективные конструкции. Лучше всего то, что он абсолютно бесплатен и доступен через ваш веб-браузер.
Бесплатный инструмент рассчитывает изгибающие моменты, силы сдвига, прогибы и реакции для заданной геометрии балки и условий нагрузки, помогая студентам и профессиональным инженерам проектировать безопасные и эффективные конструкции. Лучше всего то, что он абсолютно бесплатен и доступен через ваш веб-браузер.
Последнее обновление SkyCiv Free Beam Calculator
Недавно SkyCiv выпустила обновленную версию Free Beam Calculator с улучшенным пользовательским интерфейсом, обещая еще лучший пользовательский интерфейс. Теперь он удобен для мобильных устройств, что позволяет пользователям легко анализировать и рассчитывать лучи прямо со своих телефонов.
Благодаря новому интерфейсу этот бесплатный инструмент для работы с лучами еще никогда не был таким простым в использовании!
Калькулятор свободной балки также имеет несколько новых функций, облегчающих пользователям расчет диаграмм изгибающего момента и поперечной силы в секундах. Например, теперь пользователи могут щелкать и перетаскивать, чтобы перемещать грузы:
Например, теперь пользователи могут щелкать и перетаскивать, чтобы перемещать грузы:
Вместе с широким спектром сокращенных вводов, таких как ввод с разделителями-запятыми, математические выражения и сочетания клавиш, теперь сложный ввод уходит в прошлое!
SkyCiv Free Beam Calculator Особенности
SkyCiv Free Beam Calculator — это мощный инструмент для инженеров, подрядчиков и всех, кому необходимо выполнять расчеты луча. Калькулятор может генерировать реакции, диаграммы поперечной силы (SFD), диаграммы изгибающего момента (BMD), прогиб и расчет напряжения для консольной или просто опертой балки. Калькулятор помогает пользователям выполнить профессиональный рабочий процесс расчета балки, позволяя им просматривать и определять, соответствуют ли их расчеты региональным нормам проектирования.
Калькулятор реакции балки
Калькулятор также имеет калькулятор реакции балки, который легко вычисляет реакции на опорах как для консольных, так и для простых балок. Калькулятор включает реакции для консольных балок, в том числе реакции изгибающего момента и силы реакции x,y. Реакции на опорах полезны для определения общей силы, приложенной к конструкции.
Калькулятор включает реакции для консольных балок, в том числе реакции изгибающего момента и силы реакции x,y. Реакции на опорах полезны для определения общей силы, приложенной к конструкции.
Калькулятор изгибающего момента и силы сдвига
Еще одной ключевой функцией калькулятора свободной балки SkyCiv является калькулятор изгибающего момента и силы сдвига. Этот универсальный инструмент для проектирования конструкций используется для расчета изгибающего момента в алюминиевых, деревянных или стальных балках. Его также можно использовать в качестве калькулятора несущей способности балки, рассчитывая напряжение изгиба или напряжение сдвига. Калькулятор может учитывать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузок и 2 моментов, которые могут быть организованы как равномерно распределенные нагрузки (UDL), треугольные распределенные нагрузки или трапециевидные распределенные нагрузки. Калькулятор может учитывать наиболее распространенные ситуации расчета балки, так как все нагрузки и моменты могут быть направлены как вверх, так и вниз по величине.
Калькулятор отклонения луча
Наконец, калькулятор свободного луча SkyCiv также имеет калькулятор отклонения луча (или калькулятор смещения луча). Эта функция позволяет пользователям наблюдать расчетный прогиб свободно опертой балки или консольной балки. Калькулятор также может добавлять формы и материалы сечений, что делает его полезным в качестве калькулятора деревянных балок или калькулятора стальных балок для проектирования низкоуровневых балок или двутавровых балок. Эта функция в настоящее время доступна только в программном обеспечении SkyCiv Beam, которое предлагает еще больше возможностей для проектирования деревянных, бетонных и стальных балок.
Оцените последнюю версию SkyCiv Free Beam Calculator прямо сейчас — лучший бесплатный онлайн-инструмент для расчета момента, сдвига и отклонения балок. Если вы присматриваетесь к программному обеспечению SkyCiv, это идеальное место, чтобы познакомиться с тем, что может предложить SkyCiv Beam!
О SkyCiv
SkyCiv предлагает инженерам широкий спектр облачного программного обеспечения для структурного анализа и проектирования.