Расчет металлической балки
Двутавp колонный (К) по ГОСТ 26020-83
20К1
20К2
23К1
23К2
26К1
26К2
26К3
30К1
30К2
30К3
35К1
35К2
35К3
40К1
40К2
40К3
40К4
Двутавp с уклоном полок по ГОСТ 8239-89
10
12
14
16
18
20
22
24
27
30
33
36
40
45
50
55
60
Двутавp дополнительной серии (Д) по ГОСТ 26020-83
24ДБ1
27ДБ1
36ДБ1
35ДБ1
40ДБ1
45ДБ1
30ДШ1
40ДШ1
50ДШ1
Двутавp нормальный (Б) по ГОСТ 26020-83
10Б1
12Б1
12Б2
14Б1
14Б2
16Б1
16Б2
18Б1
18Б2
20Б1
23Б1
26Б1
26Б2
30Б1
30Б2
35Б1
35Б2
40Б1
40Б2
45Б1
45Б2
50Б2
55Б1
55Б2
60Б1
60Б2
70Б1
70Б2
80Б1
80Б2
90Б1
90Б2
100Б1
100Б2
100Б3
100Б4
Двутавp широкополочный по ГОСТ 26020-83
20Ш1
23Ш1
26Ш1
26Ш2
30Ш1
30Ш2
30Ш3
35Ш1
35Ш2
35Ш3
40Ш1
40Ш3
50Ш1
50Ш2
50Ш3
50Ш4
60Ш1
60Ш2
60Ш3
60Ш4
70Ш1
70Ш2
70Ш3
70Ш4
70Ш5
Двутавp нормальный (Б) по СТО АСЧМ 20-93
10Б1
12Б1
12Б2
14Б1
14Б2
16Б1
16Б2
18Б1
18Б2
20Б1
25Б2
30Б1
30Б2
35Б1
35Б2
40Б1
40Б2
45Б1
45Б2
50Б1
50Б2
50Б3
55Б1
55Б2
60Б1
60Б2
70Б0
70Б1
70Б2
Двутавp широкополочный (Ш) по СТО АСЧМ 20-93
20Ш1
25Ш1
30Ш1
30Ш2
35Ш1
35Ш2
40Ш2
45Ш1
50Ш1
50Ш2
50Ш3
50Ш4
60Ш1
60Ш2
60Ш3
60Ш4
70Ш1
70Ш2
70Ш3
80Ш1
80Ш2
90Ш1
90Ш2
100Ш1
100Ш2
100Ш3
100Ш4
Двутавp колонный (К) по СТО АСЧМ 20-93
20К1
20К2
25К1
25К3
30К1
30К2
30К3
30К4
35К1
35К2
40К1
40К2
40К3
40К4
40К5
Расчет балки на изгиб — Favorit-TK.
ruРассчитывать балку на изгиб можно несколькими вариантами:1. Расчет максимальной нагрузки, которую она выдержит
2. Подбор сечения этой балки
3. Расчет по максимальным допустимым напряжениям (для проверки)
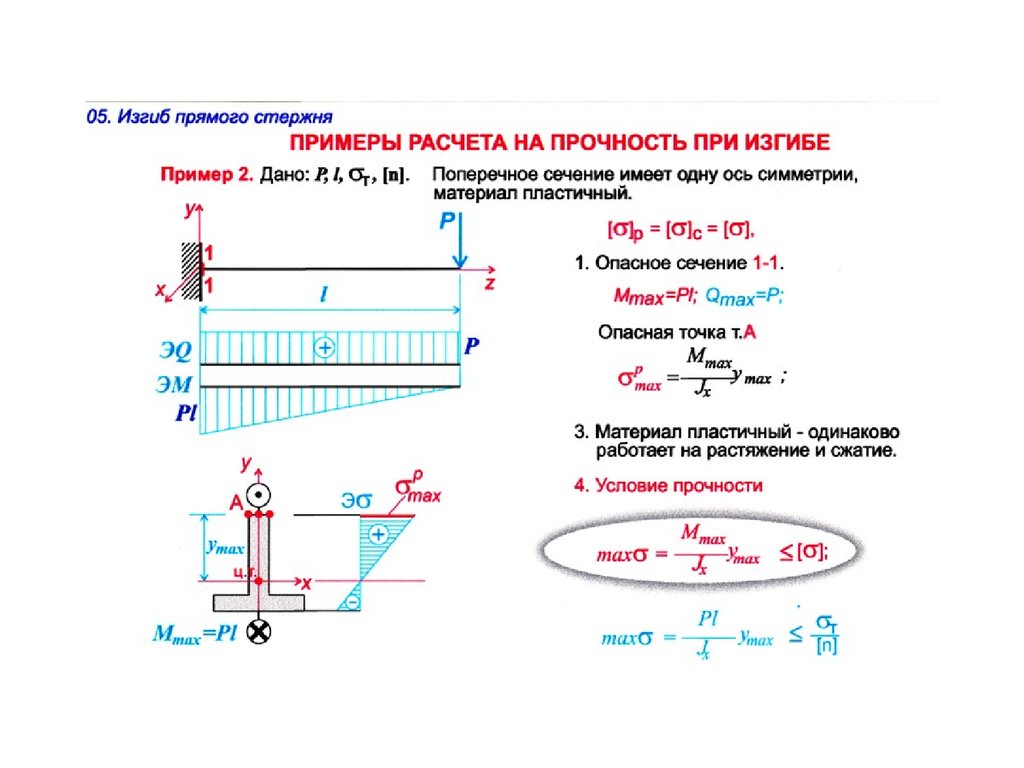
Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.
Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент. Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.
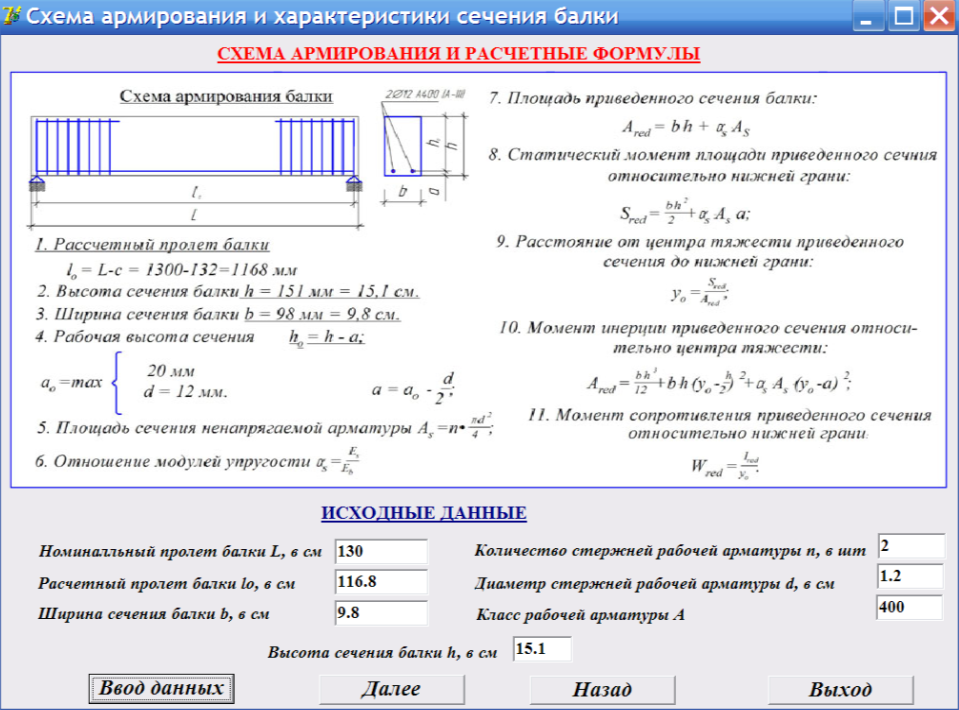
После нахождения изгибающего момента мы должны найти момент сопротивления Wx этого сечения по формуле приведенной в таблице:
Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.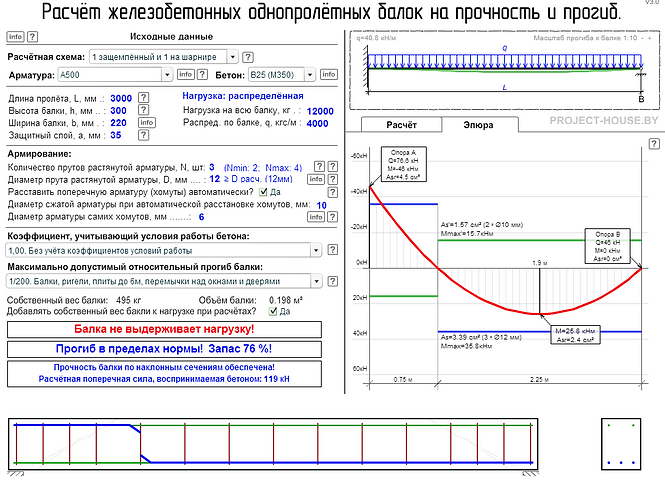
Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала, а для хрупких (чугун) – пределу прочности. Предел текучести и предел прочности мы можем найти по таблицам ниже.
1. Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.
Для начала нам необходимо выбрать расчетную схему.
На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине, то и максимальное напряжение будет в заделке.
Давайте найдем его:
P = m * g = 90 * 10 = 900 Н = 0.9 кН
М = P * l = 0.9 кН * 2 м = 1.8 кН*м
По таблице сортамента двутавров находим момент сопротивления двутавра №10.
Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.
Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.
б = М / W = 1.8 кН/м / 0.0000397 м3 = 45340 кН/м2 = 45.34 МПа
После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.
45.34 МПа < 245 МПа – верно, значит данный двутавр выдержит массу 90 кг.
2. Поскольку у нас получился довольно-таки большой запас, то решим вторую задачу, в которой найдем максимально возможную массу, которую выдержит все тот же двутавр №10 длиной 2 метра.
Если мы хотим найти максимальную массу, то значения предела текучести и напряжения, которое будет возникать в балке, мы должны приравнять (б=245 Мпа = 245 000 кН*м2).
Далее по формуле б = М / W, находим максимальный момент.
М = б * W = 245 000 * 0.0000397 = 9.73 кН * м
Тогда по формуле M = P * L найдем P:
P = 9,73 кН/м / 2м = 4,87 кН = 487 кг
Итак, максимальная масса, которую выдержит двутавр №10 – 487 кг.
Число это грубое, поскольку для простоты расчета мы не учитывали различные коэффициенты запаса, поэтому, чтобы подстраховаться, возьмите некий двукратный запас по прочности.
Диаграммы внутренних усилий для двухопорной балки
Этот онлайн-калькулятор показывает диаграммы внутренних сил для простой (двухопорной) балки, с одной стороны шарнирно закрепленной, а с другой опирающейся на ролики, под действием системы нагружения. Калькулятор графически изображает изгибающий момент M и поперечную силу Q, действующие вдоль стержня. Построение необходимо для определения положения наиболее нагруженного (опасного) участка балки.
Теория и расчетные формулы находятся под калькулятором.
Просто введите данные системы нагрузки в приведенную ниже таблицу и получите диаграммы свободного тела, поперечной силы и изгибающего момента.
Shear force and bending moment in the two-support beam
Distance between supports, m
Load
| Distance to the support A | Load | Значение | Direction | Moment direction | Range | Difference | ||
|---|---|---|---|---|---|---|---|---|
51020501001000
Нагрузка
Расстояние до опоры A
Может быть отрицательным, если нагрузка действует слева от опоры A
Сила нагрузки, кН Равномерно распределенная нагрузка, кН/м Линейно распределенная нагрузка, кН/м Момент, кН*м
Import dataImport error
«Один из следующих символов используется для разделения полей данных: табуляция, точка с запятой (;) или запятая (,)» Образец: -50,5;L;50,5;вверх;против часовой стрелки;50,5;увеличение
Загрузка данные из файла .
csv.
Перетащите файлы сюда
Показать подробности
Точность расчета
Знаки после запятой: 2
Диаграммы поперечной силы и изгибающего момента
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Внутренние силы
На следующем рисунке показаны внутренние силы в балке под нагрузкой.
Для определения внутренних сил в точке В проведем воображаемый разрез перпендикулярно оси x по осям y и z.
Схема свободного тела сечения балки выставляет внутренние силы, действующие в точке B, как внешние. Составляющая силы N B , действующая вдоль оси x, называется нормальной силой .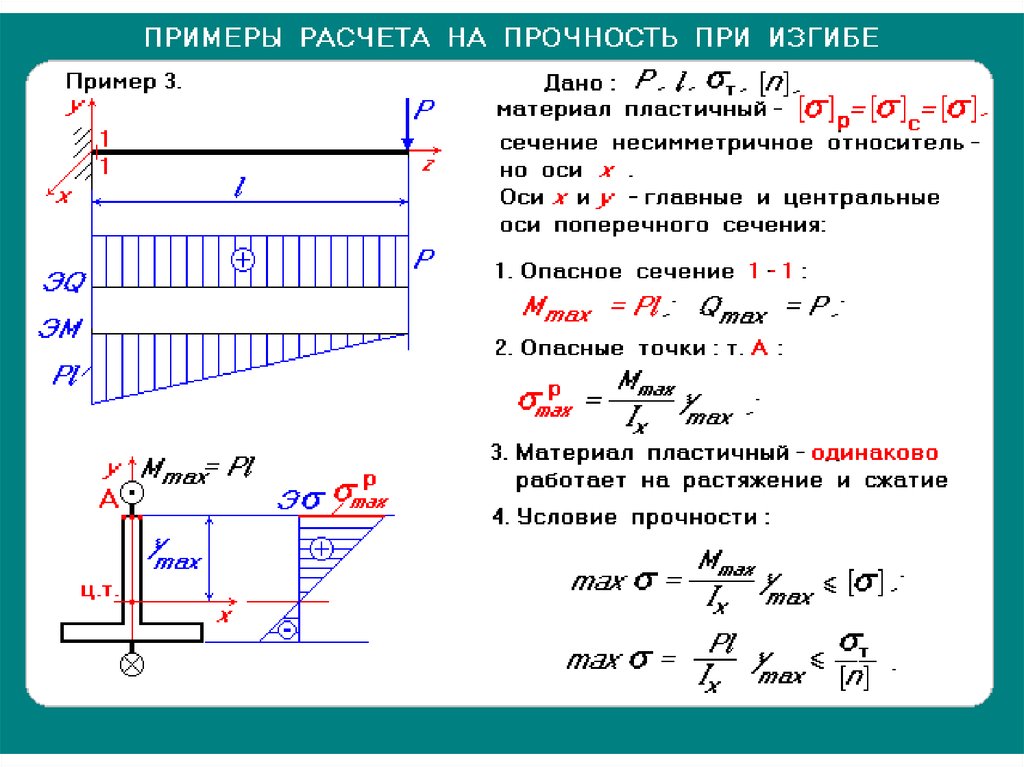
Мы пропускаем вычисление нормальной составляющей силы в калькуляторе, так как он допускает только нагрузки, действующие перпендикулярно балке.
Составляющая внутренней силы Q B , действующая параллельно поперечному сечению, называется поперечной силой . Калькулятор получает только компонент y силы шептала, потому что компонент z равен нулю для перпендикулярных нагрузок.
Парный момент M B называется изгибающим моментом .
Изгибающий момент равен сумме всех силовых моментов, приложенных к сегменту балки относительно центра тяжести сечения.
Компоненты силы препятствуют относительному переносу между двумя сегментами, а парный момент предотвращает относительное вращение. 1
Диаграммы внутренних сил путем интегрирования.
Найдем формулы для расчета значений перерезывающей силы Q(x) и изгибающего момента M(x) отдельно для разных отрезков балки.
Границы сегментов имеют выступающие точки: концы балок, места опор, точки приложения сосредоточенных сил и сосредоточенных моментов, границы распределенных нагрузок.
Для каждого сегмента вычисляется интеграл функции распределенной нагрузки q (x) для определения поперечной силы Q (x). Следующим шагом является вычисление интеграла Q(x) для определения функции изгибающего момента M(x) в соответствии с формулами:
2
Распределенная нагрузка q (x) в нашем калькуляторе может быть линейной, линейно убывающей или возрастающей. В первом случае q(x) — постоянная, во втором — линейная функция: q(x) = kx + b. При отсутствии распределенных нагрузок в сечении поперечная сила будет постоянной.
Таким образом, чтобы найти функции Q(x), а также M(x), необходимо будет получить неопределенный интеграл от многочлена и вычислить постоянную интегрирования. Константу интегрирования легко найти, если известна некоторая точка, через которую проходит искомая функция. См.: Полиномиальный интеграл.
В качестве такой точки возьмем значения Q(x) и M(x) по левой границе каждого отрезка.
Q (x l ) будет равно значению функции поперечной силы для предыдущего сегмента в крайней правой точке сегмента плюс величина сосредоточенной силы (или реакции опоры) в этой точке, если таковая имеется.
Если сила действует вверх, то изменение Q(x) положительно, в противном случае отрицательно.
M (x l ) будет равно значению функции изгибающего момента M (x) для предыдущего отрезка в его крайней правой точке, сдвинутой на величину сосредоточенного момента, приложенного к этой точке, если он есть. Если сосредоточенный момент направлен по часовой стрелке, то сдвиг положительный, в противном случае — отрицательный.
Значение Q(x) на левой кромке балки будет соответствовать сумме сосредоточенных сил и реакции опоры в этой точке или равно нулю, если таковых нет. Величина М(х) на концах балки равна сумме значений сосредоточенных моментов, приложенных к концам балки. Если в этих точках нет сосредоточенных моментов, то М(х) будет равно нулю.
Знаки М(х) и Q(х) могут быть связаны с характером деформации балки под действием внешних сил. Если изгибающий момент в сечении положительный, то балка в этом сечении изгибается выпуклостью вниз, если он отрицательный, то балка изгибается выпуклостью вверх.
Пример
Рассмотрим расчет Q(x) и M(x) на примере:
Откройте этот пример в калькуляторе.
- Во-первых, найти реакцию поддержки. Вы можете увидеть, как это сделать на этой странице.
Расчетные опорные реакции:
- Разделение балки на сегменты по ключевым точкам: 0, 2, 4, 5, 6.
Участок А — граничные точки: 0,2
Участок В — граничные точки: 2,4
Участок С — граничные точки: 4,5
Сегмент D — граничные точки: 5,6 - Для каждого сегмента:
- найти формулу распределенной нагрузки q(x)
- интегрируйте его, чтобы получить формулу силы сдвига Q(x).
- снова проинтегрируйте, чтобы получить формулу изгибающего момента M(x).
Константы интегрирования вычисляются по координате левой границы отрезка по формулам для предыдущего отрезка
Участок А, граничные значенияСегмент А
Распределенная нагрузка равна: q(x) = 5.
Интегрируем q(x), чтобы найти поперечную силу:
Найти константу интегрирования C = Q(x)+5x, в точке x=0. В норме поперечная сила на концах балки равна нулю, а на левом конце она изменяется опорной реакцией V A =11,56кН, направленной вверх. Итак, поперечная сила в точке 0 равна: Q(0) = 0 + 11,56 = 11,56.
Отсюда C = 11,56 — 5 ⋅ 0 = 11,56
Поперечная сила для сегмента А:
Интегрируя функцию поперечной силы Q(x), получаем формулу изгибающего момента:
У нас нет сосредоточенных моментов в точке 0, поэтому M( 0) = 0,
Подставляя x = 0 и M(0) = 0 в выражение для C = M(x) + 2,5x 2 — 11,56x = 0 + 2,5 · 0 2 — 11,56 0 получаем значение C = 0
Изгибающий момент для сегмента А:
Интегрируем q(x), чтобы найти поперечную силу: Участок B
Для нахождения функции распределенной нагрузки q(x) используем линейное уравнение из двух точек.
По точкам (2;0) и (4;8) находим это уравнение: q(x) = 4x-8.
Интегрируйте эту функцию, чтобы найти формулу поперечной силы.
По формуле предыдущего отрезка Q(x) вычислить Q на левой границе: Q(2)=-5∙2+11,56 = 1,56. Аналогично предыдущему отрезку найти интеграл и постоянную интегрирования по точке (2;1.56).
Формула силы сдвига на участке B:
см. расчет
Найти значение момента в точке x=2 по формуле предыдущего участка M(x): M(2) = -2,5 ∙ 2 2 + 11,56 ∙ 2 + 0 = 13,12 .
Интегрирование Q(x) и вычисление константы интегрирования по левому граничному значению получить формулу изгибающего момента для отрезка B:
см. расчет
отрезок C
Рассчитать поперечную силу в точке 4 по отрезку B поперечную силу Q(x) по формуле: Q(4 ) = -2 ∙ 4 2 + 8 ∙ 4 – 6,44 = -6,44.
Сосредоточенная сила F 1=4кН резко меняет значение Q(x) в точке x=4. Она направлена вниз, поэтому сложение отрицательное: Q(4) = -6,44 — 4 = -10,44
На этом отрезке нет распределенной нагрузки, поэтому поперечная сила постоянна.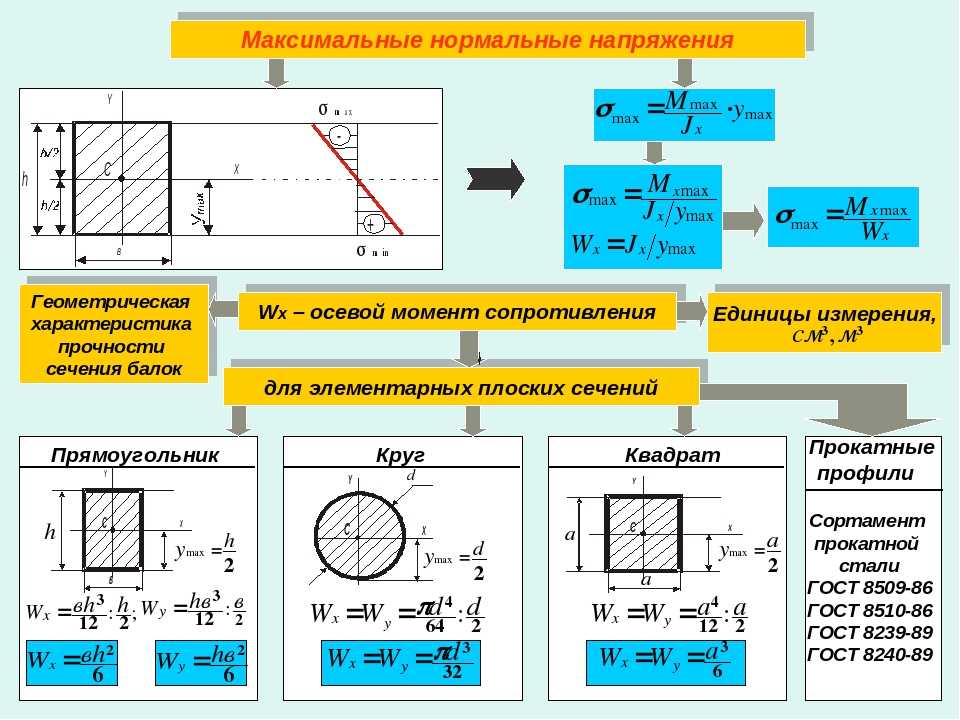
Формула поперечной силы на участке С:
Значение изгибающего момента в точке x=4 рассчитывается по формуле M (x) для предыдущего участка: M(4) = -0,67 ∙ 4 3 + 4 ∙ 4 2 – 6,44 ∙ 4 + 15,33 = 10,91
Интегрируем Q(x) и вычисляем C по граничному значению получаем формулу изгибающего момента отрезка С:
см. расчет
Участок 909 Поскольку распределенной нагрузки нет, поперечная сила вдоль этого отрезка постоянна.
Сила сдвига на участке D:
Рассчитать граничное значение M(5) по предыдущей формуле M(x): M(5) = -10,44 ∙ 5 + 52,67 = 0,47
Сосредоточенный момент M 1 изменений M х на данный момент. Сосредоточенный момент направлен по часовой стрелке, поэтому сложение положительное: M(5) = 0,47 + 10 = 10,47
Интегрируем Q(x) и получаем C получаем формулу изгибающего момента для сегмента D:
см.
расчет Найдите самый правый Q (x) и M(x), чтобы убедиться, что мы нашли правильную формулу:
Абсолютное значение поперечной силы равно значению реакции опоры в этой точке. Как и ожидалось, изгибающий момент на конце балки равен нулю.
R.C.Hibbeler Инженерная механика. Статика 12-е издание, стр. 330 ↩
Н. М. Беляев. Сопротивление материалов, М.: «Наука», 1965, выпуск 14, стр. 231 ↩
диаграмма изгибающего момента балки Инженерная сила сдвига сопротивление материалов теоретическая механика
Калькулятор для инженеров — изгибающий момент и поперечная сила для кантилевера
Калькуляторы CE > Изгибающий момент и поперечная сила для кантилевера
Калькулятор изгибающего момента и поперечная сила для кантилевера
Этот бесплатный онлайн-калькулятор разработан, чтобы предоставить программный инструмент для расчета
из
Изгиб
Момент и поперечная сила в любом сечении
консольная балка, подвергаемая
точечная нагрузка, равномерно распределенная нагрузка и переменная нагрузка.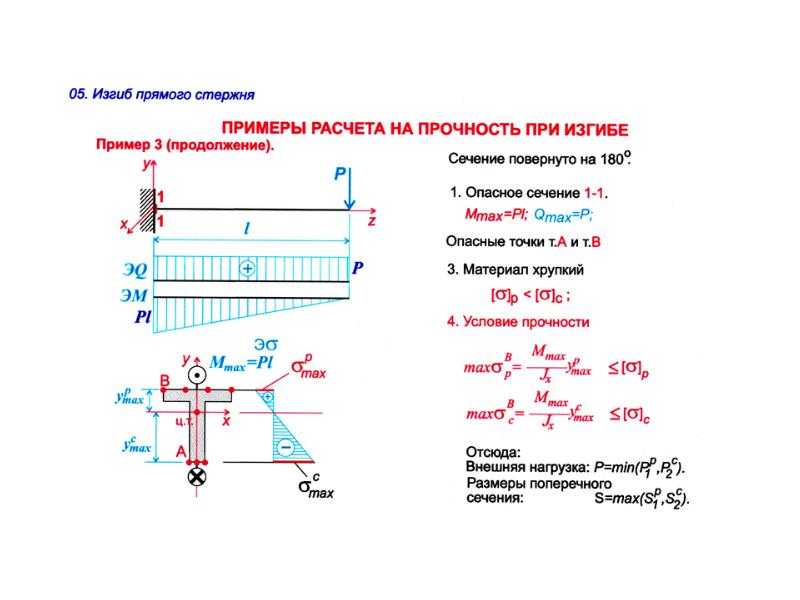
Вы можете скопировать и вставить результаты этих калькуляторов в файл документа.
С помощью этого калькулятора также можно найти ординаты диаграммы влияния для структуры.
Вы можете выбрать один из вариантов нагрузки, приведенных ниже, или перейти к инструкциям для SF и BM консоли для получения дополнительной информации
Варианты нагрузки для консоли
Точечная нагрузка включена
Консоль
UDL с левой стороны
УДЛ на
часть пролета
UDL с правой стороны
UDL на полном пролете
Переменная нагрузка на полном пролете
Вы также можете посетить следующие ссылки по теме
Проба 5-1 Диаграмма изгибающего момента и поперечной силы для кантилевера
Характер кривой для диаграммы изгибающего момента
Диаграмма изгибающего момента для нависающей балки
Excellent Calculators
Калькулятор преобразования напряжения
Расчет главного напряжения, максимального напряжения сдвига и их плоскостей Б.