Расчёт балки, рамы бесплатно онлайн

|
Лимит расчётов:
Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки или рамы и позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с готовым решением. Удачи! | |
Расчет балки онлайн
Для расчета балок первым делом необходимо определить усилия, возникающие в конструкциях. В данном разделе показано, как находить усилия, опорные реакции, прогибы и углы поворота в различных изгибаемых конструкциях. Для самых распространенных из них вы можете воспользоваться онлайн расчетом. Для редких — приведены все формулы определения необходимых значений.
Онлайн расчет балки на двух опорах (калькулятор).
Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.
Синие ячейки — ввод данных. (Белые ячейки — ввод координаты для определения промежуточного итога).
Зеленые ячейки — расчетные, промежуточный итог.
Оранжевые ячейки — максимальные значения.
>>> Перейти к расчету балки на двух опорах <<<
Онлайн расчет консольной балки (калькулятор).
Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.
Синие ячейки — ввод данных. (Белые ячейки — ввод координаты для определения промежуточного итога).
Зеленые ячейки — расчетные, промежуточный итог.
Оранжевые ячейки — максимальные значения.
>>> Перейти к расчету консольной балки <<<
Расчет однопролетной балки на двух шарнирных опорах.

Рис.1 Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке

Рис.2 Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках

Рис.3 Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке

Рис4. Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке

Рис5. Расчет балки на двух шарнирных опорах при действии изгибающего момента
Расчет балок с жестким защемлением на двух опорах

Рис6. Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке

Рис7. Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках

Рис8. Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке

Рис9. Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке

Рис10.Расчет балки с жестким защемлением на опорах при действии изгибающего момента
Расчет консольных балок
Рис11. Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке

Рис12. Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке

Рис13. Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке
Рис14. Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента
Расчет двухпролетных балок

Рис15. Расчет двухпролетной балки с шарнирными опорами при одной сосредоточенной нагрузке

Рис16. Расчет двухпролетной балки с шарнирными опорами при одной равномерно-распределенной нагрузке

Рис17. Расчет двухпролетной балки с шарнирными опорами при одной неравномерно-распределенной нагрузке
Онлайн расчет статически неопределенной балки
Расчет выполняется методом сил
Канонические уравнения метода сил:
Где коэффициенты системы определяются:
Принцип ввода данных, рассмотрим с помощью следующего примера:
1. Задание длины (12м) и условий закрепления стержня. Левый конец стержня свободен, а правый — жестко закрепленный. Задаем координаты опор (отсчет ведется от левого конца стержння). Первая опора имеет координату 2м, вторая — 7м.
2. Задаем нагрузки, использовав соответствующие правила знаков:
3. В случае, если жесткость балки переменная, задайте необходимые пропорции (нажмите на кнопку «Изменить жесткость»):
4. Для начала расчета нажмите на кнопку «Построить эпюры».
Для расчета балок используется следующая основная система (ОС). Выбрать ОС невозможно.
Решение системы уравнений:
Опорные реакции:
Расчёт балки бесплатно онлайн
Закрыть
Примечание. Иллюстрации в отчёте сформированы шириной в 420px (диалог «Настройки»).
Исходные данные
|
|
Расчёт

|
| Рис. 2. Схема реакций |

|
| Рис. 3. Эпюра Qy, кН (поперечная сила) |

|
| Рис. 4. Эпюра Mx, кН·м (изгибающий момент) |
1. Определение реакций опор
Составим уравнения статического равновесия.
∑Fy = -q·7м — F + YA + YB = 0;
∑MA = -q·7м·3.5м + M — F·10м + YB·7м = 0.
Решение уравнений статики даёт следующие значения реакций:
YA = 36кН;
YB = 67кН.
2. Построение эпюр внутренних силовых факторов
Участок №1 (0 ≤ z1 ≤ 7м)
Qy = YA — q·z1;
при z1 = 0; Qy = 36кН.
при z1 = 7м; Qy = -48кН.
Mx = YA·z1 — q·z12/2;
при z1 = 0; Mx = 0.
при z1 = 3м; Mx = 54кН·м.
при z1 = 7м; Mx = -42кН·м.
Участок №2 (0 ≤ z2 ≤ 3м)
Qy = F = 19кН.
Mx = M — F·z2;
при z2 = 0; Mx = 15кН·м.
при z2 = 3м; Mx = -42кН·м.
Закрыть
Расчет балок онлайн. Примеры расчета
Расчет балки различается в зависимости от того, является она статически определимой, либо статически неопределимой. На сайте производится расчет любых балок, но подробное решение расписывается только для статически определимых балок, не имеющих промежуточных шарниров.
Балка на двух опорах. Построение эпюр
Для этого типа балок сервис позволяет определить и подробно расписывает:
- реакции опор
- эпюры поперечных сил и изгибающих моментов (эпюры Q и M)
- подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
- строятся эпюры нормальных и касательных напряжений
- по уравнениям метода начальных параметров вычисляются прогибы и углы поворота. Записываются и сами уравнения метода начальных параметров по участкам.
Посмотреть пример »
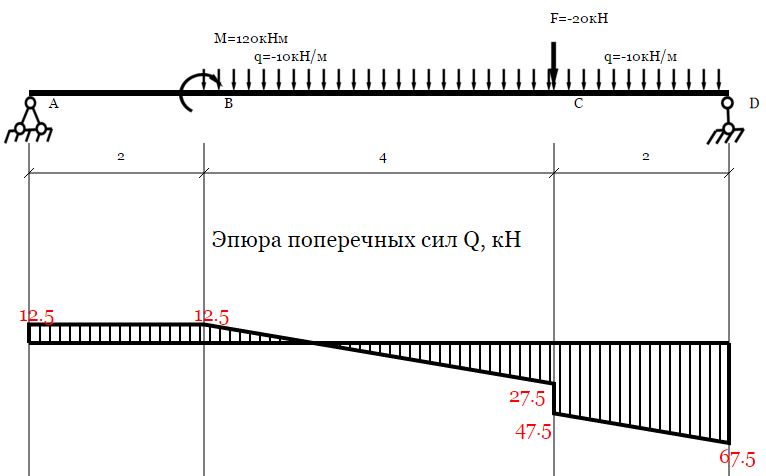
Консольная балка. Построение эпюр.
Для этого типа балок сервис позволяет определить и подробно расписывает:
- построение эпюр поперечных сил и изгибающих моментов
- подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
- строятся эпюры нормальных и касательных напряжений
- вычисляются прогибы и углы поворота.
Посмотреть пример »
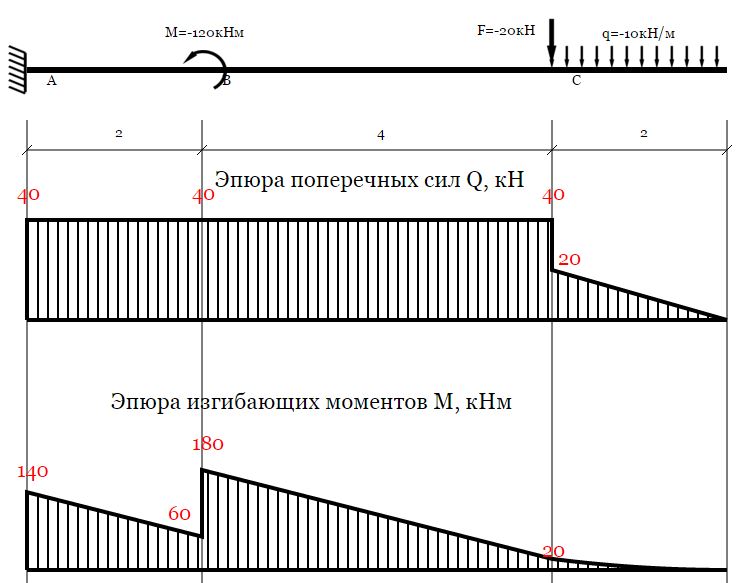
Статически неопределимая балка. Подбор сечения.
Для такого типа балок Вы можете получить
- только результаты расчета — (эпюры Q и M).
Естественно, по этим эпюрам можно легко найти реакции опор. Подробный ход расчета не расписывается, но, имея результаты, Вы легко можете проверить все промежуточные итоги своего расчета.
Посмотреть пример »
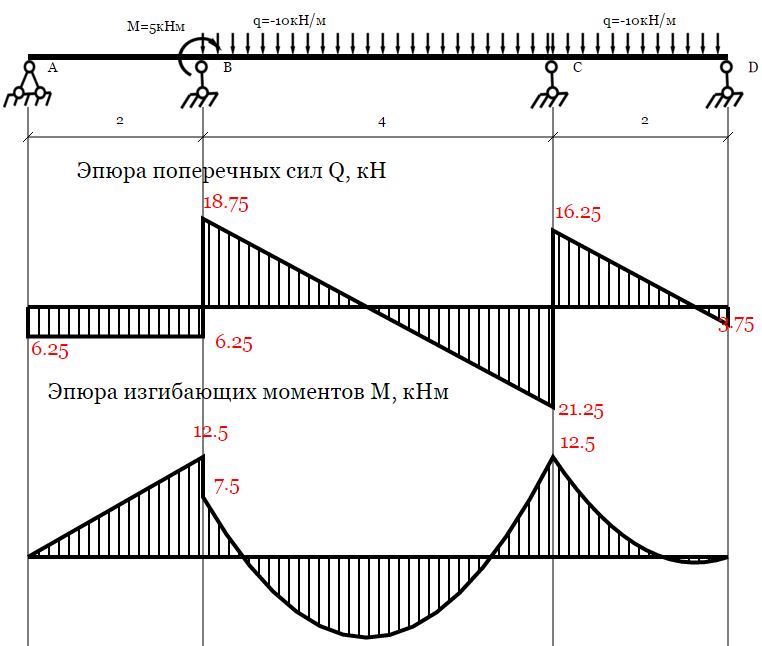
Балка с промежуточными шарнирами
Расчет балки с промежуточными шарнирами Вы должны производить, скорее всего, методом построения поэтажной схемы. Сервис, опять же, дает только конечный результат, но его наличие, естественно, очень упрощает проверку промежуточных этапов решения заданий.
Посмотреть пример »
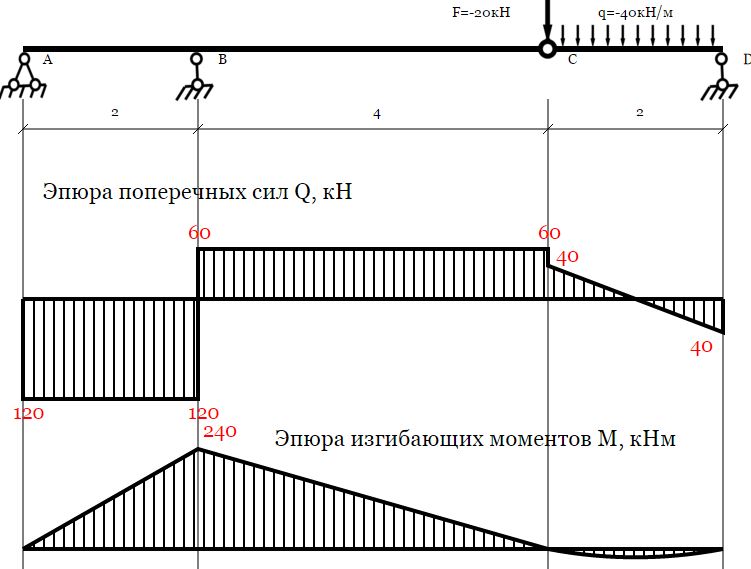
| КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ ЧЛЕНОВ | |
| Калькулятор | Определение |
| Конструкция компрессионных элементов (изгиб колонны) | |
| ПРОСТАЯ ПОДДЕРЖКА РАСЧЕТЫ ДЕФЛЕКЦИИ | |
| Просто поддерживаемая балка с несколькими точечными / распределенными нагрузками и моментами | |
| Просто поддерживаемая балка с сосредоточенной нагрузкой в любой точке | |
| Просто поддерживаемый луч с двумя Point Loads | |
| Просто поддерживаемая балка с частично распределенной промежуточной нагрузкой | |
| Просто поддерживаемая балка с двумя частично распределенными промежуточными нагрузками | |
| Просто поддерживаемый луч с моментом | |
| Просто поддерживаемый луч с двумя моментами | |
| CANTILVER BEAM РАСЧЕТЫ ДЕФЛЕКЦИИ | |
| Консольная балка с несколькими точечными / распределенными нагрузками и моментами | |
| Консольная балка с одиночной нагрузкой | |
| Калькулятор отклонения луча — сплошные прямоугольные балки, полые прямоугольные балки, сплошные круглые балки Введите значение и нажмите «Рассчитать». Результат будет отображаться | |||||||||||||||||||||||||||
| Рассчитать прогиб для сплошных прямоугольных балок Рассчитать прогиб полых прямоугольных балок Рассчитать прогиб для сплошных круглых балок Рассчитать прогиб для круглых трубных балок | |||||||||||||||||||||||||||
Рассчитать прогиб для сплошных прямоугольных балок
| |||||||||||||||||||||||||||
Рассчитать прогиб полых прямоугольных балок
| |||||||||||||||||||||||||||
Рассчитать прогиб для сплошных круглых балок
| |||||||||||||||||||||||||||
Расчет прогиба для круглых трубных балок
| |||||||||||||||||||||||||||
балок — поддерживается на обоих концах
Напряжение в изгибающем балке можно выразить как
σ = y M / I (1)
, где
σ = напряжение (Па (Н / м ) 2 ), Н / мм 2 , фунт / кв.дюйм)
y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = изгибающий момент (Нм, фунт-дюйм)
I = момент инерции (м 4 , мм 4 , в 4 )
Приведенный ниже калькулятор можно использовать для расчета максимального напряжения и прогиба балок при одной или одинаковых распределенных нагрузках.
, поддерживаемый с обеих сторон — равномерная непрерывная распределенная нагрузка
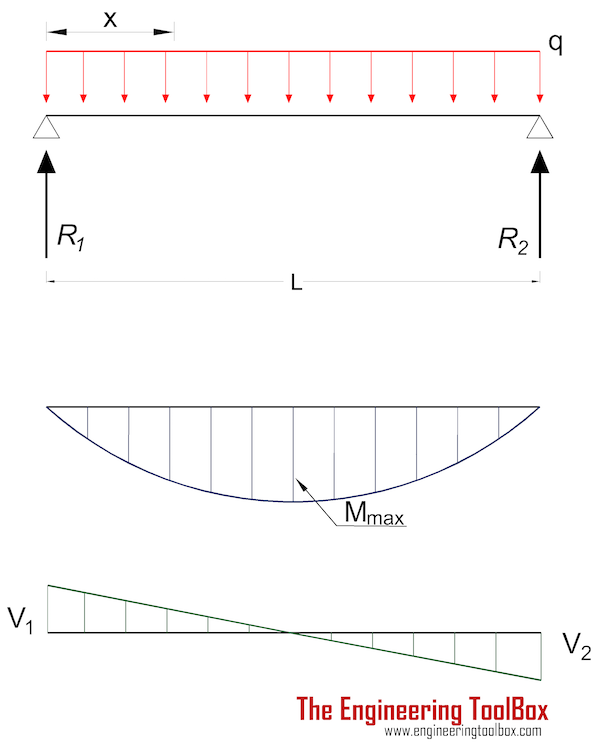
Момент в балке с равномерной нагрузкой, поддерживаемой на обоих концах в положении x, может быть выражен как
M x = qx (L — x) / 2 (2)
, где
M x = момент в положении x (Нм, фунт-дюйм)
x = расстояние от конца (м, мм, дюйм)
Максимум момент находится в центре луча на расстоянии L / 2 и может быть выражен как
M max = q L 2 /8 (2a)
, где
M макс. = максимальный момент ( Нм, фунт-дюйм)
q = равномерная нагрузка на единицу длины балки (Н / м, Н / мм, фунт / дюйм)
9000 2 L = длина балки (м, мм, дюйм)Максимальное напряжение
Уравнения 1 и 2a можно объединить, чтобы выразить максимальное напряжение в балке с равномерным нагрузка поддерживается на обоих концах на расстоянии L / 2, как
макс. = у макс. кв. л 2 / (8 I) (2b)
, где
а макс = максимальное напряжение (Па (Н / м 2 ), Н / мм 2 , фунт / кв.дюйм)
y макс = расстояние до крайней точки от нейтральной оси (м, мм, дюйм)
- 1 Н / м 2 = 1×10 -6 Н / мм 2 = 1 Па = 1.4504×10 -4 фунтов на квадратный дюйм
- 1 фунт / кв.дюйм (фунт / дюйм 2 ) = 144 фунта на кв. Дюйм (фунт f / фут 2 ) = 6 894,8 Па (н / м 2 ) = 6,895×10 — 3 Н / мм 2
Максимальное отклонение :
δ макс = 5 q L 4 / (384 EI) (2c)
, где
δ макс. = максимальное отклонение (м, мм, дюйм)
E = Модуль упругости (Па (Н / м 2 ), Н / мм 2 , фунт / кв.дюйм)
Отклонение в положении x:
δ x = qx ( L 3 — 2 L x 2 + x 3 ) / (24 EI) (2d)
Примечание! — прогиб часто является ограничивающим фактором в конструкции балки.Для некоторых применений лучи должны быть сильнее, чем требуется максимальными нагрузками, чтобы избежать недопустимых отклонений.
Силы, действующие на концах:
R 1 = R 2
= q L / 2 (2e)
, где
R = реактивная сила (Н, фунт)
Пример — Балка с равномерной нагрузкой, метрические единицы
A Балка UB 305 x 127 x 42 длиной 5000 мм несет равномерную нагрузку 6 Н / мм .Момент инерции для балки составляет 8196 см. 4 (81960000 мм 4 ) , а модуль упругости для стали, используемой в балке, составляет 200 ГПа (200000 Н / мм 2 ) , Высота луча составляет 300 мм (расстояние от крайней точки до нейтральной оси составляет 150 мм ).
Максимальное напряжение в балке можно рассчитать
σ макс = (150 мм) (6 Н / мм) (5000 мм) 2 / (8 (81960000 мм 4 ))
= 34.3 Н / мм 2
= 34,3 10 6 Н / м 2 (Па)
= 34,3 МПа
Максимальный прогиб в пучке можно рассчитать
δ макс. = 5 (6 Н / мм) (5000 мм) 4 / (( 200000 Н / мм 2 ) ( 81960000 мм 4 ) 384)
= 2,98 мм
Калькулятор балок с равномерной нагрузкой — метрические единицы
- 1 мм 4 = 10 -4 см 4 = 10 -12 м 4
- 1 см 4 = 10 -8 м = 10 4 мм
- 1 в 4 = 4.16×10 5 мм 4 = 41,6 см 4
- 1 Н / мм 2 = 10 6 Н / м 2 (Па)
Калькулятор с равномерной нагрузкой — имперские единицы
Пример— Балка с равномерной нагрузкой, имперские единицы
Максимальное напряжение в стальной широкофланцевой балке «W 12 x 35», длина 100 дюймов, длина , момент инерции 285, 4 , модуль упругости 2 σ макс = y макс q L 2 / (8 I) = (6.25 дюймов) (100 фунтов / дюйм) (100 дюймов) 2 / (8 (285 в 4 )) = 2741 (фунт / дюйм 2 , фунтов на квадратный дюйм) Максимальное отклонение может рассчитывается как δ макс = 5 кв. л 4 / (EI 384) = 5 (100 фунтов / дюйм) (100 дюймов) 4 / ((2 = 0,016 в Максимальный момент в балке с центральной нагрузкой, поддерживаемой в обоих заканчивается: M макс. = FL / 4 (3a) Максимальное напряжение в балке с одной центральной нагрузкой, поддерживаемой на обоих концах: σ Макс. = y макс. FL / (4 I) ( 3b) , где F = нагрузка (Н, фунт) Максимальное отклонение можно выразить как δ Макс. = FL 3 / (48 EI) (3c) Силы, действующие на концах: R 1 = R 2 = F / 2 (3d) Максимальное напряжение в стальной широкофланцевой балке «W 12 x 35», длина 100 дюймов, длина , момент инерции 285, 4 , модуль упругости эластичность 2 σ макс. = y макс. FL / (4 I) = (6.25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 в 4 )) = 5482 (фунт / в 2 , фунтов на квадратный дюйм) Максимальный прогиб можно рассчитать как δ макс. = FL 3 / EI 48 = (10000 фунтов / дюйм) (100 дюймов) 3 / ((2 = 0,025 в Максимальный момент в балке с одной эксцентричной нагрузкой при точка нагрузки: M max 9 0050 = F ab / L (4a) Максимальное напряжение в балке с одинарной центральной нагрузкой, поддерживаемой на обоих концах: σ Макс = y макс F ab / (LI) (4b) Максимальный прогиб в точке нагрузки может быть выражен как δ F = F a 2 b 2 / (3 EIL) (4c) Силы, действующие на заканчивается: R 1 = F b / L (4d) R 2 = F a / L (4e) Максимальный момент (между нагрузками) в балке с двумя эксцентриковыми нагрузками: M max = F a (5a) Максимальное напряжение в балке с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах: σ макс = y макс F a / I (5b) макс. прогиб в точке нагрузки может быть выражен как δ F = F a (3L 2 — 4 a 2 ) / (24 EI) (5c) Силы, действующие на концах: R 1 = R 2 = F (5d) Вставьте балки в модель Sketchup с помощью Extension Toolbox Box Sketchup Максимальный момент (между нагрузками) в балке с тремя точечными нагрузками: 9000 3 M max = FL / 2 (6a) Максимальное напряжение в балке с трехточечными нагрузками, поддерживаемыми на обоих концах: σ max = y max FL / (2 I) (6b) Максимальный прогиб в центре балки можно выразить как δ F = FL 3 / (20.22 E I) (6c) Силы, действующие на концах: R 1 = R 2 = 1,5 F (6d) или Открыть Стресс в любой точке Напряжение в центре постоянного сечения прогиб в любой точке Максимальный прогиб в центре с общей нагрузкой «W» или Максимальный прогиб в центре с нагрузкой давления в линии «p» Где: E = (Н / мм 2) I = W = с = у = x = Z = z = Рекомендации: Поддерживаемый луч на обоих концах — нагрузка в центре
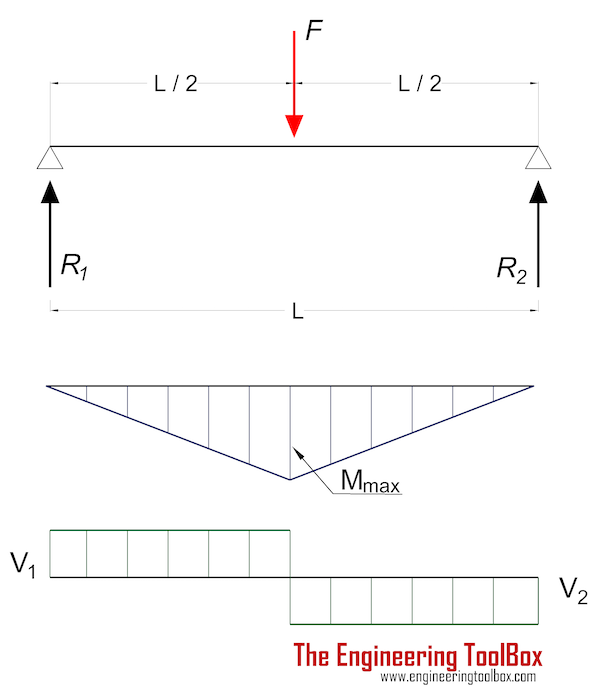
Максимальное напряжение
Калькулятор одноцентровой балки нагрузки — метрические единицы
Калькулятор одноцентровой балки нагрузки — Imperial Units
Пример — Балка с одиночной центральной нагрузкой
Некоторые типичные вертикальные пределы отклонения
Балка, поддерживаемая с обеих сторон — эксцентрическая нагрузка
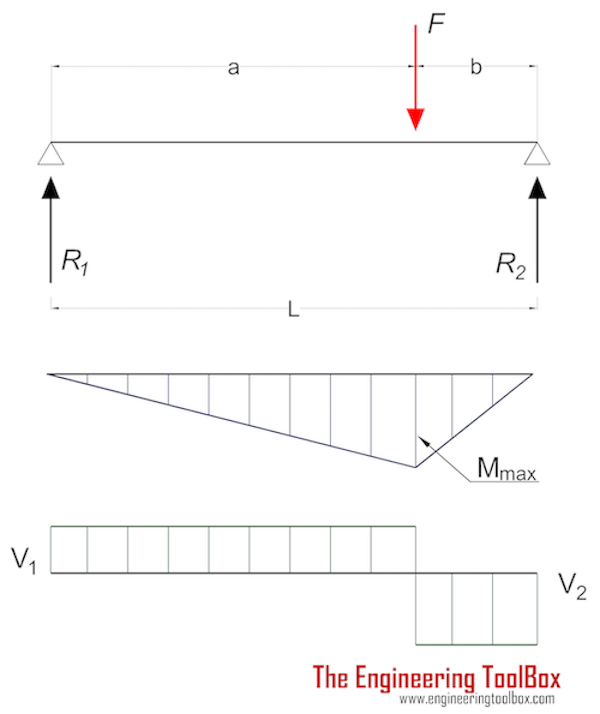
Максимальное напряжение
Поддерживаемая на обоих концах балка — два эксцентриковых груза
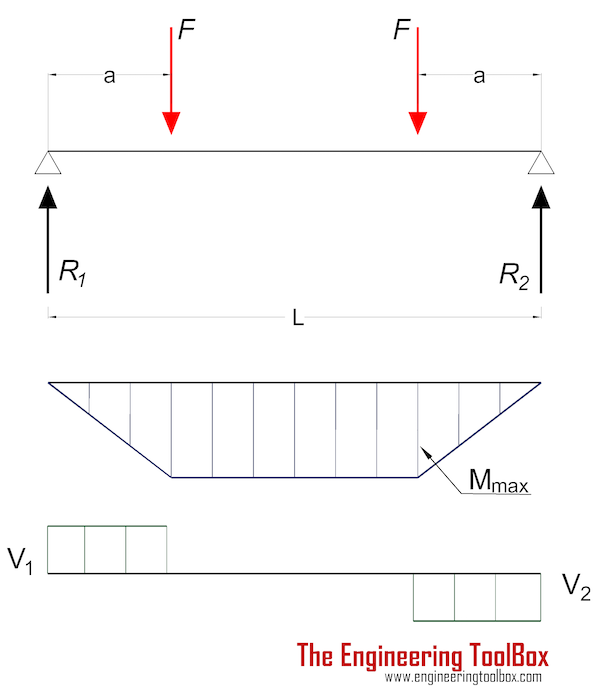
Максимальное напряжение
Балка, поддерживаемая на обоих концах — трехточечные нагрузки
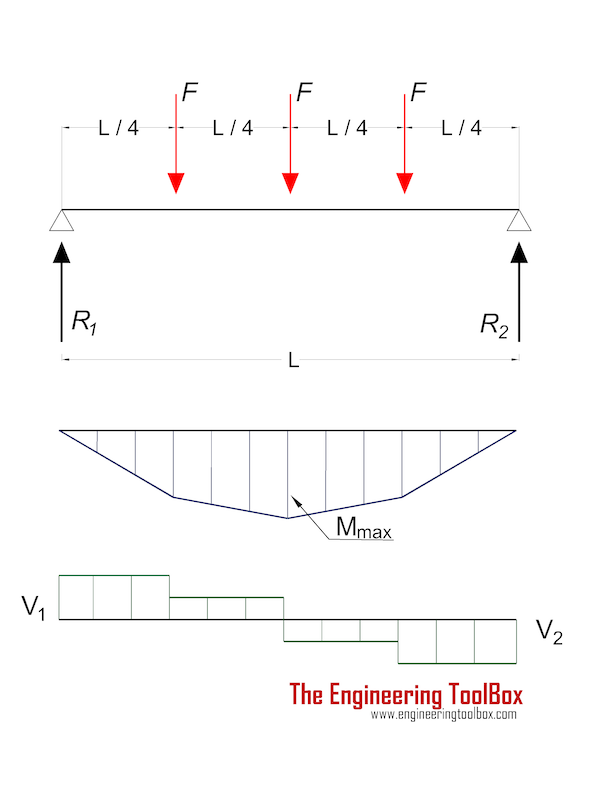
Максимальное напряжение
.
Общая нагрузка («W»)
Линейная нагрузка (p)
Прогиб балки, калькулятор нагрузки с равномерной нагрузкой Модуль упругости фунтов на квадратный дюйм Момент инерции в 4 (мм 4) = Длина луча дюймов (мм) Общая нагрузка на балку фунтов (N) р = с линейной нагрузкой фунтов на квадратный дюйм (Н / мм) Напряжение в поперечном сечении оценивается фунтов / в 2 (Н / мм 2) прогиб дюймов (мм) Некоторое расстояние, как указано дюймов (мм) модуль сечения поперечного сечения балки = I / Z в 3 (мм 3) расстояние от нейтральной оси до крайности
волокно (край) дюймов (мм) Навигация по записям



