- Как рассчитать площадь космических фигур
- Как вычислить площадь пространственной фигуры?
- Какова общая площадь пространственной фигуры?
- Как рассчитать объем пространственных фигур?
- Как рассчитать общую площадь объекта?
- Что такое космические фигуры?
- Как рассчитать призмы и пирамиды?
- Какова площадь помещения?
- Как сделать геометрические расчеты?
- Чем отличаются плоские фигуры от пространственных?
- Чему равна площадь сферы?
- По какой формуле вычисляется площадь основания?
- Как рассчитать общую площадь призмы?
- Что такое площадь фигуры?
- Чему равна площадь параллелепипеда?
- Какова площадь куба?
- Как объяснить пространственные геометрические фигуры?
- Как рассчитывается объем?
- Сколько граней у пространственной фигуры?
- Что такое формулы призмы?
- Что такое многоугольники?
- Сколько граней у параллелепипеда?
- Как рассчитать квадратную площадь помещения?
- Что такое пояснительная область?
- В чем разница между площадью и пространством?
- Зачем считать площадь?
- По какой формуле вычисляется площадь треугольника?
- Как вычислить площадь прямоугольника?
- Как вычислить площадь и периметр плоских фигур?
- Почему куб не плоская фигура?
- Какие плоские фигуры образуют пространственную фигуру?
- Как вычислить площадь равностороннего треугольника?
- Как вычислить площадь цилиндра?
- Какова площадь квадрата?
- Каков объем шара?
- Что такое номер PI?
- Как рассчитать площадь шестиугольной призмы?
- По какой формуле вычисляется объем куба?
- Как вычислить площадь шестиугольника?
- Как рассчитать квадратную площадь помещения?
- Чему равна площадь сферы?
- Как вычислить площадь многогранника?
- Как рассчитать площадь трехмерного объекта?
- Как вычислить площадь помещения сложной формы: методики расчета
- | 16 популярных форм!
- Что такое площадь в математике? Определение площади
- Как рассчитать площадь?
- Формула площади квадрата
- Формула площади прямоугольника
- Формула площади треугольника
- Формула площади круга
- Формула площади сектора
- Формула площади эллипса
- Формула площади трапеции
- Площадь параллелограмма формула
- Формула площади ромба
- Формула площади воздушного змея
- Формула площади пятиугольника
- Формула площади шестиугольника
- Формула площади восьмиугольника
- Площадь кольца формула
- Формула площади четырехугольника
- Формула площади правильного многоугольника
- Часто задаваемые вопросы
- Калькулятор площади 📐 - Рассчитайте площадь квадрата, прямоугольника, треугольника, круга, параллелограмма, трапеции...
Как рассчитать площадь космических фигур
содержание
Как вычислить площадь пространственной фигуры?
Площадь фигуры получается умножением основания (b) на высоту (h). А объем определяется путем умножения высоты на ширину и длину.
Какова общая площадь пространственной фигуры?
Площадь измеряет площадь поверхности плоской фигуры (основание, умноженное на высоту), а периметр измеряет ее контур (сумма сторон). Объем, с другой стороны, измеряет занимаемое пространство, поэтому он относится к пространственной геометрии и определяется путем умножения трех измерений.
Как рассчитать объем пространственных фигур?
Чтобы найти объем тела, надо площадь основания умножить на высоту. Помните, что основание фигуры может принимать различные размеры (треугольники, четырехугольники, пятиугольники, шестиугольники, семиугольники и другие).
Как рассчитать общую площадь объекта?
Площадь является важной величиной в геометрии. Для заданной геометрической фигуры площадь равна площади поверхности этой фигуры. Для вычисления площади плоских фигур используем специфические формулы для каждой из них, при необходимости делим плоскую фигуру на известные плоские фигуры и складываем площади.
Для вычисления площади плоских фигур используем специфические формулы для каждой из них, при необходимости делим плоскую фигуру на известные плоские фигуры и складываем площади.
Что такое космические фигуры?
Особенности пространственной геометрии
- призма.
- Куб.
- брусчатка.
- пирамида.
- конус.
- цилиндр.
- мяч.
Как рассчитать призмы и пирамиды?
Даны призма и пирамида с одинаковым основанием, мы знаем, что объем призмы равен произведению площади основания на высоту, а объем пирамиды равен произведению площади основание и высота делятся на три, поэтому при одинаковой площади основания объем пирамиды будет равен 1/3 объема призмы.
Какова площадь помещения?
Площадь — это математическое понятие, которое можно определить как количество двумерного пространства, то есть поверхности.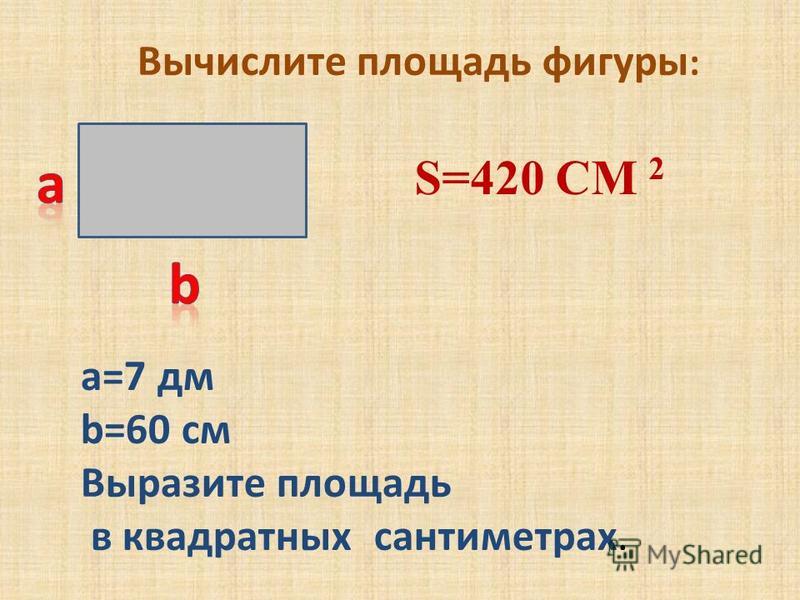
Как сделать геометрические расчеты?
Формулы для каждой геометрической фигуры:
- Преобразование единиц измерения: π рад равно 180°. Длина круга: C = 2 · π · R. Площадь круга: A = π · R2
- Боковая площадь конуса: Š = π · R. грамм.
- Площадь основания цилиндра: Ab = π · r2 Площадь боковой поверхности цилиндра: Al = 2·π·r·h.
Чем отличаются плоские фигуры от пространственных?
Планиметрия — это изучение фигур в двух измерениях, таких как квадраты, круги, прямоугольники и треугольники. В то время как пространственная геометрия изучает фигуры в трех измерениях, то есть кубы, сферы, параллелепипеды и пирамиды.
Чему равна площадь сферы?
Для расчета площади поверхности шара используйте следующую формулу:SE = 4 . π . г²
г²
По какой формуле вычисляется площадь основания?
Расчет площади основания
Площадь основания (АB) призмы зависит от образующего ее многоугольника. Поскольку в призме у нас есть две параллельные и конгруэнтные грани, площадь основания определяется суммой площадей параллельных многоугольников, то есть удвоенной площадью многоугольника.
Как рассчитать общую площадь призмы?
Площадь призмы можно вычислить, сложив площадь ее стороны и площади оснований. Процесс вычисления этих площадей в конечном итоге облегчается тем, что два основания призмы одинаковы, поэтому достаточно вычислить площадь основания и умножить результат на 2.
Что такое площадь фигуры?
Площадь плоской фигуры – это мера ее поверхности. Для расчета площади плоской фигуры разработаны специальные формулы, зависящие от формы фигуры. Формула площади треугольника. Площадь плоской фигуры – это площадь поверхности фигуры.
Формула площади треугольника. Площадь плоской фигуры – это площадь поверхности фигуры.
Чему равна площадь параллелепипеда?
Общая площадь параллелепипеда вычисляется по формуле АT = 2аб + 2ас + 2бс.
Какова площадь куба?
Поскольку куб состоит из шести равных квадратов, общая площадь куба в шесть раз больше площади его основания.
Как объяснить пространственные геометрические фигуры?
Пространственные геометрические фигуры – это те, которые имеют три измерения: длину, высоту и ширину. Эти фигуры делятся на две группы: круглые тела (ограниченные какой-либо округлой поверхностью) и многогранники (поверхности, ограниченные плоскими геометрическими фигурами).
Как рассчитывается объем?
Расчет объема всегда производится путем умножения высоты (h), на ширину (L), и на длину (L).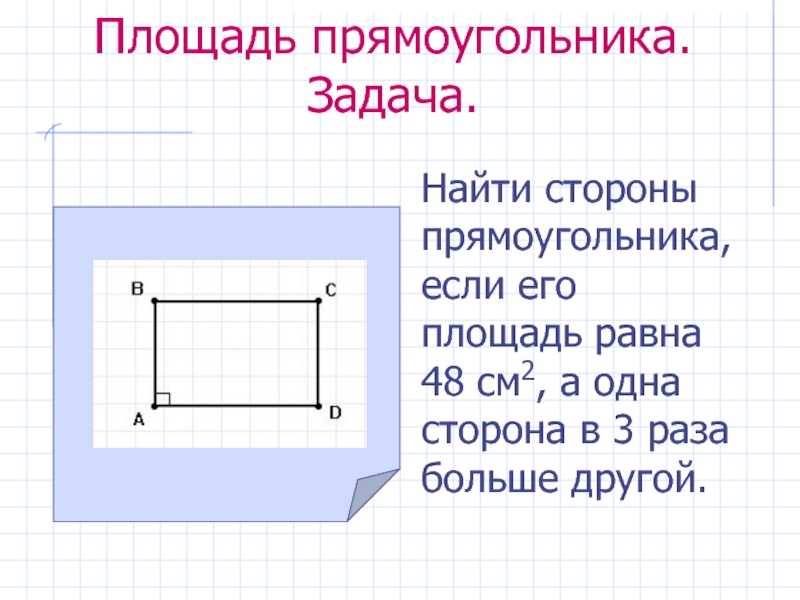
Сколько граней у пространственной фигуры?
Сколько граней у пространственной фигуры? Грани: у него 6 квадратных граней; Диагонали: внутри куба 4 диагонали; Вершины: имеет 8 вершин; Углы: 24 прямых угла.
Что такое формулы призмы?
Для проверки общей площади площади боковых граней и площади оснований необходимо сложить следующим образом: At = S1 + 2Sb, где S1 — сумма площадей боковых граней, а 2Sb — сумма площадей базы. Объем должен быть рассчитан следующим образом: V=Ab. h, считая Ab площадью основания и «h» высотой.
Что такое многоугольники?
Многоугольник
- Многоугольники, образованные 3 (треугольник), 4 (четырехугольник), 5 (пятиугольник) и 6 (шестиугольник) сегментов линии.
- Части многоугольника.
- Выпуклый многоугольник и вогнутый многоугольник.
- Не полигоны.
Сколько граней у параллелепипеда?
Параллелепипед – это геометрическое тело, грани которого образованы параллелограммами. Он состоит из 8 вершин, 12 ребер и 6 граней. Он классифицируется как прямой, если его края перпендикулярны, и как косой, если его края не перпендикулярны.
Он состоит из 8 вершин, 12 ребер и 6 граней. Он классифицируется как прямой, если его края перпендикулярны, и как косой, если его края не перпендикулярны.
Как рассчитать квадратную площадь помещения?
Измерение, соответствующее внутреннему пространству
Так как у квадрата равные стороны, просто измерьте одну из сторон и возведите ее в квадрат. Для реализации воспользуемся формулой площади A = b. h, поэтому одна из его сторон будет основанием (b), а другая — высотой (h).
Что такое пояснительная область?
Площадь — это общая мера поверхности, то есть все пространство, которое она занимает на плоскости, а не только ее контур. А чтобы уметь вычислять площадь плоской фигуры надо анализировать фигуру и знать, с какой из них мы имеем дело.
В чем разница между площадью и пространством?
Площадь — это мера пространства на двумерной плоскости, определяемой границей. Например, площадь — это мера всего замкнутого пространства футбольного поля.
Зачем считать площадь?
Площадь используется для вычисления меры плоской поверхности, а периметр используется для вычисления суммы мер сторон фигуры или объекта.
По какой формуле вычисляется площадь треугольника?
Площадь треугольника – это измерение его поверхности, которую можно вычислить, умножив основание на высоту и разделив на два, рассматривая любой треугольник.
Как вычислить площадь прямоугольника?
Прямоугольник является частным случаем четырехугольника, входящего в группу тех, у которых все углы прямые. Чтобы вычислить площадь прямоугольника, достаточно вычислить произведение между его основанием и высотой, то есть площадь дается формулой A=b⋅h. Помимо площади, еще одной важной величиной является периметр.
Как вычислить площадь и периметр плоских фигур?
Как правило, чтобы найти площадь фигуры, просто умножьте основание (b) на высоту (h). Периметр – это сумма отрезков, образующих фигуру, называемых сторонами (l).
Почему куб не плоская фигура?
Это потому, что куб трехмерен, а плоскость двумерна. Место или «пространство», где могут быть построены трехмерные фигуры, также называется пространством. В нем можно строить фигуры, имеющие ширину, длину и глубину.
В нем можно строить фигуры, имеющие ширину, длину и глубину.
Какие плоские фигуры образуют пространственную фигуру?
Плоские и пространственные фигуры
- КРУГ, очень круглый;
- ТРЕУГОЛЬНИК – геометрическая фигура с тремя сторонами.
- КВАДРАТ имеет четыре стороны, и все они одинаковой длины.
- ПРЯМОУГОЛЬНИК имеет четыре стороны, но не все они одинаковы.
Как вычислить площадь равностороннего треугольника?
Чтобы найти площадь равностороннего треугольника, умножьте квадрат длины стороны на корень из 3, деленный на 4.
Как вычислить площадь цилиндра?
В прямом круговом цилиндре площадь поперечного сечения определяется выражением A(широта)=2πrh, где r — радиус основания, а h — высота цилиндра. Общая площадь соответствует сумме боковой площади и удвоенной площади основания.
Какова площадь квадрата?
Площадь квадрата, частного случая четырехугольника, можно вычислить, возведя его сторону в квадрат. Площадь квадрата равна длине его стороны в квадрате. Площадь квадрата измеряется его поверхностью и может быть рассчитана путем возведения его стороны в квадрат.
Площадь квадрата измеряется его поверхностью и может быть рассчитана путем возведения его стороны в квадрат.
Каков объем шара?
Формула объема сферы: V = 4/3 πr³.
Что такое номер PI?
Это число является константой, и его значение приблизительно равно 3,141592653…, но наиболее часто используемое приближение для значения π равно 3,14.
Как рассчитать площадь шестиугольной призмы?
При этом площадь призмы с шестиугольным основанием равна A = 2Ah + 6Ar, где:
- Ah – площадь шестиугольника;
- Воздух – площадь стороны прямоугольника.
По какой формуле вычисляется объем куба?
Следовательно, объем куба зависит только от меры его ребра. Объем куба равен длине ребра, возведенного в 3, то есть V = a³.
Как вычислить площадь шестиугольника?
Шестиугольник – это правильный шестиугольник. Мы можем разделить этот многоугольник на 6 одинаковых треугольников. Итак, чтобы найти площадь этого шестиугольника, достаточно найти площадь одного из треугольников, а затем умножить результат на 6.
Добавьте метраж спереди и сзади и разделите на 2, а затем добавьте метраж сторон и разделите на 2. Умножьте эти 2 значения, и вы получите площадь земли в квадратных футах.
Один из способов состоит в том, чтобы разделить площадь большей фигуры на два прямоугольника разного размера, вычислив таким образом площадь двух прямоугольников по отдельности, умножив два заданных размера. Сложите две найденные площади и таким образом получите общую площадь фигуры.
Чтобы вычислить площадь любого треугольника, просто вычислите произведение между длиной основания и высотой и разделите на два: Пример: Вычислите площадь треугольника с основанием, равным 30 см, и высотой, равной 22. см.
Как рассчитать квадратную площадь помещения?
Измерение, соответствующее внутреннему пространству
Так как у квадрата равные стороны, просто измерьте одну из сторон и возведите ее в квадрат. Для реализации воспользуемся формулой площади A = b. h, поэтому одна из его сторон будет основанием (b), а другая — высотой (h).
Чему равна площадь сферы?
Для расчета площади поверхности шара используйте следующую формулу:SE = 4 . π . г²
Как вычислить площадь многогранника?
Площадь многогранника и, следовательно, куба равна сумме площадей образующих его многоугольников. Складывая все эти площади, можно найти формулу вычисления площади куба, что нас и интересует. Однако сначала необходимо знать, что площадь многогранника делится на площадь основания и площадь стороны.
Как рассчитать площадь трехмерного объекта?
Порядок расчета площади 3D-поверхностей такой же, как и для 2D-объектов. Нажмите «Инструменты», «Запрос», «Область», введите «O» (объект), ENTER и выберите. Надеюсь это поможет.
Как вычислить площадь помещения сложной формы: методики расчета
Перед тем как начать работы по укладке напольного покрытия и отделке стен, необходимо определить потребный объем материала. Для этого определяется площадь помещения и квадратура стен. Полученные данные можно использовать и в других целях.
Рассчитать метраж довольно просто, если стены и пол идеально ровные, а также отсутствуют дополнительные архитектурные детали. Например, эркеры. Но такие условия встречаются лишь в панельных домах постройки середины прошлого века. В этом случае формула расчета м2 упрощается до умножения длины на ширину. Сегодня же мы расскажем о том, как вычислить площадь в домах нестандартных проектов с комнатами сложной формы.
Измерения — основа расчетов
Чтобы посчитать площадь, надо произвести измерения. Это банально. Однако дело это не такое простое, как кажется. Чтобы получить правильные результаты, необходимо придерживаться двух правил:
-
Использовать эталонные инструменты.
-
Получать результат минимальным количеством подходов.
Что значит эталонный измерительный инструмент? Это тот, чьи показания имеют наименьшую погрешность.
Про число подходов. Если вы будете измерять длину комнаты ученической линейкой (кстати говоря, этот вид продукции наименее точен), то приложите ее к полу порядка тридцати раз. При этом погрешность измерения будет накапливаться. Поэтому лучше использовать строительную рулетку — результат за один раз. Наибольшей точностью обладают лазерные средства измерений расстояний. Но не все умеют ими пользоваться и они довольно дороги.
Перед началом измерения площади пола вам надо определиться с базой. Ею является самая длинная и ровная стена. Точкой отсчета на ней лучше выбрать угол — неважно, ближе к двери или дальше от нее.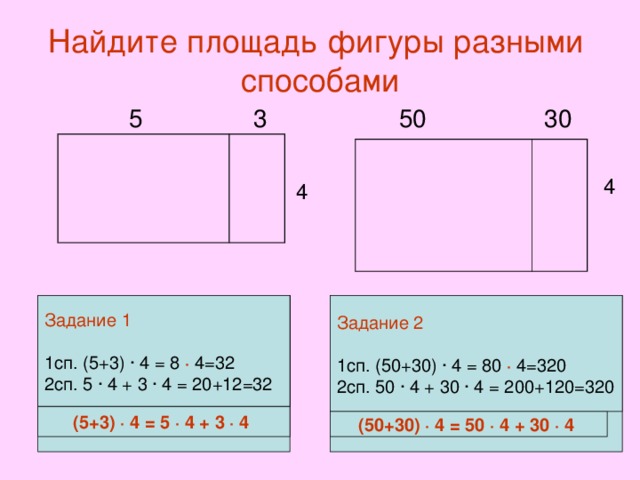
Сначала определите длину базы. Запишите ее на листе бумаги, не надеясь на память. После этого постройте перпендикуляры от нее через каждый метр, начиная от края. Для этого используйте обрезок плиты ДСП с фабричным углом, точно равным 900. Длина стороны этого своеобразного инструмента должна быть не менее метра.
Линии лучше рисовать маркером с толщиной кончика от 1 до 2 мм и цветом, контрастным с поверхностью. Чтобы не искать среди похожих царапин. Продолжите перпендикуляры до противоположной стены, используя длинную строительную линейку — ее называют правило. Обычно такой инструмент объединяют с жидкостным уровнем (ватерпасом).
Найдите самый короткий перпендикуляр и отложите от базы это расстояние по всем отмеченным линиям. Через полученные точки проведите линию, параллельную базе. Измерьте ее и сравните обе величины. Запишите все результаты, а еще лучше — нарисуйте простенький эскиз. Он позволит вам увидеть, насколько форма пола в комнате отличается от идеального прямоугольника и близка к трапеции.
Эркеры в комнатах измеряются отдельно. Если они прямоугольные, то по методике, указанной выше. Для скругленных надо определить радиус. Для этого поделите пополам последний примыкающий к ним перпендикуляр от базовой стены.
Измерение стен производят от проложенных на полу перпендикуляров и базовых линий. В точках их пересечений прочертите вертикальные линии, используя строительную линейку с жидкостным уровнем. Определите их длину и запишите там же, где вы сохранили результаты измерений пола. После этого измерьте оконные и дверные проемы, сохранив данные.
Потолок обычно равен по площади полу. Однако встречаются сложные случаи, когда и здесь есть разница. Это происходит в том случае, если стены имеют отклонения от вертикали. Обратите внимание на такой факт при их разметке.
Методика расчета площади, квадратуры и кубатуры
Используя результаты измерений, сделайте эскиз пола и стен на листе бумаги в клеточку, но лучше использовать так называемую миллиметровку.
Рассчитывать вручную по формулам лучше при небольших объемах вычислений. При этом вам помогут сетевые сервисы, которые содержат онлайн-калькуляторы разных величин, в том числе площади и объема разных фигур и тел. Квадратуру стен считают сразу всю, без учета площади дверных и оконных проемов — конечный результат получают их вычитанием из общего значения.
Многие модели лазерных дальномеров имеют функции вычислений площади на основе данных измерений. Однако этот метод больше подходит профессионалам. Потому что и сами приборы довольно дороги, и навык обращения с ними нарабатывается не сразу.
Метод с использованием палетки интересен тем, что позволяет обойтись без формул вообще.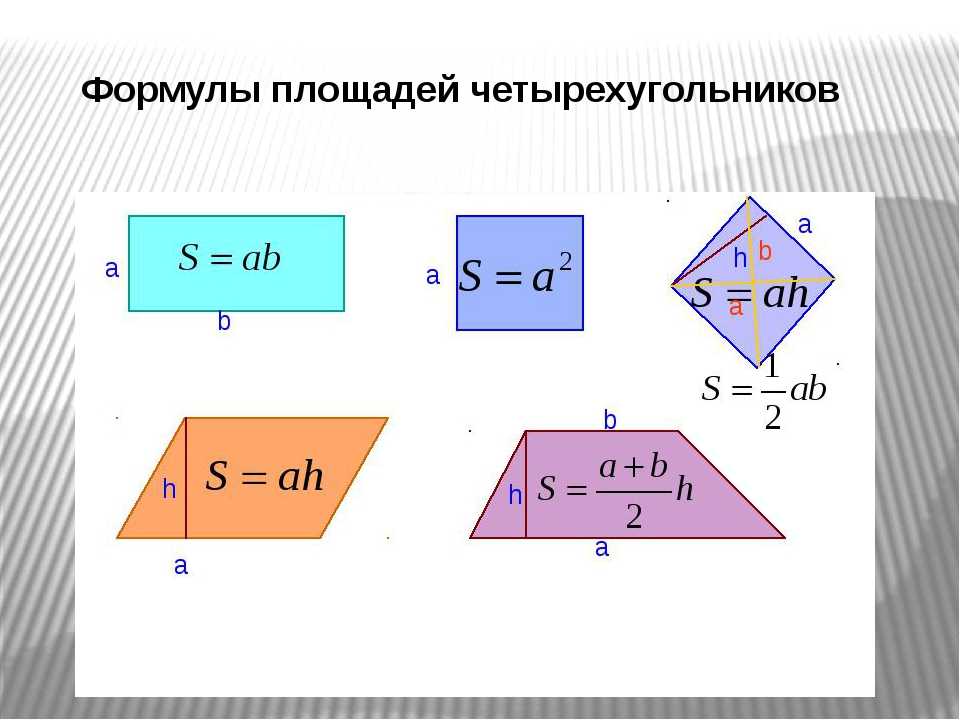 Он не очень точен, но быстр и прост. Его применяют, например, при вычислении площади участков на географических картах. В этом случае на прозрачном материале делается сетка с клеточками, имеющими известный размер в соответствии с масштабом. Например, сто на сто метров. Приложив палетку к карте, вы считаете количество целых квадратиков, а потом — обрезанных. Первые складываете как есть, а сумму вторых делите пополам. Если вы начертите эскиз пола и стен на миллиметровой бумаге, то сможете сделать такой расчет за несколько минут. Точность в пределах ± 10%.
Он не очень точен, но быстр и прост. Его применяют, например, при вычислении площади участков на географических картах. В этом случае на прозрачном материале делается сетка с клеточками, имеющими известный размер в соответствии с масштабом. Например, сто на сто метров. Приложив палетку к карте, вы считаете количество целых квадратиков, а потом — обрезанных. Первые складываете как есть, а сумму вторых делите пополам. Если вы начертите эскиз пола и стен на миллиметровой бумаге, то сможете сделать такой расчет за несколько минут. Точность в пределах ± 10%.
Расчет площади пола, квадратуры стен и кубатуры помещения может пригодиться не только при определении потребного количества материалов для ремонта. Но также для вычисления мощности кондиционеров, системы теплый пол и решения других задач по повышению комфортности проживания.
Калькулятор площади| 16 популярных форм!
Создано Hanna Pamuła, PhD
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 02 ноября 2022 г.
- Что такое площадь в математике? Определение площади
- Как рассчитать площадь?
- Формула площади квадрата
- Формула площади прямоугольника
- Формула площади треугольника
- Формула площади круга
- Формула площади сектора
- Формула площади эллипса
- Формула площади трапеции
- Формула площади параллелограмма
- Формула площади ромба
- Формула площади воздушного змея
- Формула площади пятиугольника
- Формула площади шестиугольника
- Формула площади восьмиугольника
- 0 формула
- Площадь четырехугольника формула
- Формула площади правильного многоугольника
- Часто задаваемые вопросы
Если вам интересно, как вычислить площадь любой базовой фигуры, вы находитесь в правильном месте — этот калькулятор площади ответит на все ваши вопросы. Используйте наш интуитивно понятный инструмент, чтобы выбрать одну из шестнадцати различных фигур и вычислить их площадь в мгновение ока. Ищете ли вы определение площади или, например, площадь формулы ромба, мы обеспечим вас. Продолжайте прокручивать, чтобы узнать больше, или просто поиграйте с нашим инструментом — вы не будете разочарованы!
Ищете ли вы определение площади или, например, площадь формулы ромба, мы обеспечим вас. Продолжайте прокручивать, чтобы узнать больше, или просто поиграйте с нашим инструментом — вы не будете разочарованы!
Что такое площадь в математике? Определение площади
Проще говоря, площадь — это размер поверхности . Другими словами, его можно определить как пространство, занимаемое плоской формой. Чтобы понять концепцию, обычно полезно представить площадь как количество краски, необходимое для покрытия поверхности . Посмотрите на рисунок ниже – все фигуры имеют одинаковую площадь, 12 квадратных единиц:
Существует множество полезных формул для вычисления площади простых фигур. В разделах ниже вы найдете не только известные формулы для треугольников, прямоугольников и окружностей, но и другие формы, такие как параллелограммы, воздушные змеи или кольца.
Мы надеемся, что после этого объяснения у вас не возникнет проблем с определением области математики!
Как рассчитать площадь?
Ну конечно, это  Для ясности мы перечислим только уравнения — их изображения, пояснения и выводы можно найти в отдельных абзацах ниже (а также в инструментах, посвященных каждой конкретной фигуре).
Для ясности мы перечислим только уравнения — их изображения, пояснения и выводы можно найти в отдельных абзацах ниже (а также в инструментах, посвященных каждой конкретной фигуре).
Вы готовы? Вот самые важные и полезные формулы площади для шестнадцати геометрических фигур:
- Квадрат формула площади:
A = a² - Прямоугольник Формула площади:
A = a × b -
-
А = b × h / 2или -
A = 0,5 × a × b × sin(γ)или -
A = 0,25 × √( (a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))или -
A = a² × sin(β) × sin(γ) / (2 × sin(β + γ))
-
- Круг формула площади:
A = πr² - Сектор круга Формула площади:
A = r² × угол / 2 - Эллипс формула площади:
A = a × b × π - Трапеция Формула площади:
A = (a + b) × h / 2 - Формулы площади параллелограмма :
-
А = а × чили -
A = a × b × sin(угол)или -
A = e × f × sin(угол)
-
- Ромб Формулы площади:
-
А = а × чили -
А = (е × f) / 2или -
A = s² × sin(угол)
-
- Кайт формулы площади:
-
А = (е × f) / 2или -
А = а × b × sin(γ)
-
- Формула площади Пентагона :
A = a² × √(25 + 10√5) / 4 - Шестиугольник Формула площади:
A = 3/2 × √3 × a² - Октагон формула площади:
A = 2 × (1 + √2) × a² - Формула площади кольца :
A = π(R² - r²) - Четырехугольник формула площади:
A = e × f × sin(угол) - Правильный многоугольник Формула площади:
A = n × a² × cot(π/n) / 4
Хотите изменить единицу площади? Просто нажмите на название устройства, и появится раскрывающийся список.
Формула площади квадрата
Вы забыли, что такое формула площади квадрата? Тогда вы находитесь в правильном месте. Площадь квадрата равна произведению длины его сторон:
-
Площадь квадрата = a × a = a², гдеa— сторона квадрата
Это самая основная и наиболее часто используемая формула, хотя существуют и другие. Например, есть формулы площади квадрата, в которых используются диагональ, периметр, радиус описанной окружности или внутренний радиус.
Формула площади прямоугольника
Формула площади прямоугольника тоже несложна — это просто произведение сторон прямоугольника:
-
Площадь прямоугольника = a × b
Расчет площади прямоугольника чрезвычайно полезен в повседневных ситуациях: от строительства здания (оценка необходимой плитки, настила, сайдинга или определения площади крыши) до отделки вашей квартиры (сколько мне нужно краски или обоев?) до расчета, сколько люди, которых ваш торт может накормить.
Формула площади треугольника
Существует много различных формул для площади треугольника, в зависимости от того, что дано и какие законы или теоремы используются. В этом калькуляторе площади мы реализовали четыре из них:
1. Даны основание и высота
-
Площадь треугольника = b × h / 2
2. Даны две стороны и угол между ними (SAS)
-
Площадь треугольника = 0,5 × a × b × sin(γ)
3. Даны три стороны (SSS) (Эта формула площади треугольника называется Формула Герона )
-
Площадь треугольника = 0,25 × √( (a + b + c) × (-a + b + в) × (а - б + в) × (а + б - в))
Вы можете узнать больше в калькуляторе формул Герона.
4. Даны два угла и сторона между ними (ASA)
-
Площадь треугольника = a² × sin(β) × sin(γ) / (2 × sin(β + γ))
Существует особый тип треугольника, прямоугольный треугольник. В этом случае основание и высота — это две стороны, образующие прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:
В этом случае основание и высота — это две стороны, образующие прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:
Площадь прямоугольного треугольника = a × b / 2
Формула площади круга
Формула площади круга является одной из самых известных формул:
-
Площадь круга = πr², гдеr— радиус круга
В этом калькуляторе мы реализовали только это уравнение, но в нашем калькуляторе круга вы можете рассчитать площадь по двум разным формулам:
- Диаметр
-
Площадь круга = πr² = π × (d / 2)²
- Окружность
-
Площадь круга = c² / 4π
Кроме того, формула площади круга удобна в повседневной жизни – например, при решении серьезной дилеммы, какой размер пиццы выбрать.
Формула площади сектора
Формулу площади сектора можно найти, взяв пропорцию окружности. Площадь сектора пропорциональна его углу, поэтому, зная формулу площади круга, мы можем написать, что:
Площадь сектора пропорциональна его углу, поэтому, зная формулу площади круга, мы можем написать, что:
α / 360° = площадь сектора / площадь круга
Преобразование угла говорит нам, что 360° = 2π
α / 2π = Площадь сектора / πr²
Итак:
-
Площадь сектора = r² × α / 2
Формула площади эллипса
Чтобы найти формулу площади эллипса, сначала вспомните формулу площади круга: πr² . Для эллипса у вас есть не одно значение радиуса, а два разных значения: a и b . Единственная разница между формулами площади круга и эллипса заключается в замене r² произведением большой и малой полуосей, a × b :
-
Площадь эллипса = π × a × b
Формула площади трапеции
Площадь трапеции можно найти по следующей формуле:
-
Площадь трапеции = (a + b) × h / 2, гдеaи- 74 длины параллельных сторон
ивысота
Кроме того, формула площади трапеции может быть выражена как:
Площадь трапеции = m × h , где м — среднее арифметическое длин двух параллельных сторон
Площадь параллелограмма формула
Хотите ли вы вычислить площадь, зная основание и высоту, стороны и угол, или диагонали параллелограмма и угол между ними, вы находитесь в правильном месте. В нашем инструменте вы найдете три формулы площади параллелограмма:
В нашем инструменте вы найдете три формулы площади параллелограмма:
1. Основание и высота
-
Площадь параллелограмма = a × h
2. Стороны и угол между ними
-
Площадь параллелограмма = a × b × sin(α)
3. Диагонали и угол между ними
-
Площадь параллелограмма = e × f × sin(θ)
Формула площади ромба
Мы реализовали три полезные формулы для вычисления площади ромба. Вы можете найти площадь, если знаете:
1. Сторона и высота
-
Площадь ромба = a × h
2. Диагонали
-
Площадь ромба = (e × f) / 2
3. Сторона и любой угол, например, α
-
Площадь ромба = a² × sin(α)
Формула площади воздушного змея
Для расчета площади воздушного змея можно использовать два уравнения, в зависимости от того, что известно:
1. Формула площади воздушного змея с учетом диагоналей воздушного змея
Формула площади воздушного змея с учетом диагоналей воздушного змея
-
Площадь воздушного змея = (e × f) / 2
2. Площадь воздушного змея по формуле с двумя неконгруэнтными сторонами и углом между этими двумя сторонами
-
Площадь воздушного змея = a × b × sin(α)
Формула площади пятиугольника
Площадь пятиугольника можно рассчитать по формуле:
-
Площадь пятиугольника = a² × √(25 + 10√5) / 4, где- сторона 9007 правильный пятиугольник
Воспользуйтесь нашим специальным калькулятором пятиугольника, где представлены другие основные свойства правильного пятиугольника: сторона, диагональ, высота и периметр, а также радиус описанной и вписанной окружности.
Формула площади шестиугольника
Основная формула площади шестиугольника:
-
Площадь шестиугольника = 3/2 × √3 × a², где a — сторона правильного шестиугольника
Итак, откуда берется формула? Вы можете думать о правильном шестиугольнике как о наборе шести конгруэнтных равносторонних треугольников. Чтобы найти площадь шестиугольника, нам нужно найти площадь одного треугольника и умножить ее на шесть. Формула площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленному на 4:
Чтобы найти площадь шестиугольника, нам нужно найти площадь одного треугольника и умножить ее на шесть. Формула площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленному на 4:
Площадь равностороннего треугольника = (a² × √3) / 4
Площадь шестиугольника = 6 × Площадь равностороннего треугольника = 6 × (a² × √3) / 4 = 3/2 × √3 × a²
Формула площади восьмиугольника
Чтобы найти площадь восьмиугольника, все, что вам нужно сделать, это знать длину стороны и следующую формулу:
-
Площадь восьмиугольника = 2 × (1 + √2) * a²
Площадь восьмиугольника также может быть рассчитана по формуле:
Площадь восьмиугольника = периметр × апофема / 2
Периметр в восьмиугольном случае — это просто 8 × a . А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны. В то же время это высота треугольника, полученного путем проведения линии из вершин восьмиугольника в его центр. Этот треугольник — один из восьми конгруэнтных — является равнобедренным, поэтому его высота может быть рассчитана, например, с помощью теоремы Пифагора по формуле:
В то же время это высота треугольника, полученного путем проведения линии из вершин восьмиугольника в его центр. Этот треугольник — один из восьми конгруэнтных — является равнобедренным, поэтому его высота может быть рассчитана, например, с помощью теоремы Пифагора по формуле:
h = (1 + √2) × a / 4
Итак, наконец, мы получаем первое уравнение:
Площадь восьмиугольника = периметр * апофема / 2 = (8 × a × (1 + √2) × a / 4) / 2 = 2 × (1 + √2 ) × a²
Площадь кольца формула
Кольцо представляет собой кольцеобразный объект – область, ограниченную двумя концентрическими окружностями разного радиуса. Найти площадь по формуле кольца несложно, если вы помните формулу площади круга. Только взгляните: площадь кольца — это разность площадей большего круга радиуса R и меньшего круга радиуса r:
-
Площадь кольца = πR² - πr² = π(R² - r²)
Формула площади четырехугольника
Формула четырехугольника, которую реализует этот калькулятор площади, использует две заданные диагонали и угол между ними.
-
Площадь четырехугольника = e × f × sin(α), гдеeиf— диагонали.
Мы можем использовать любой из двух углов при вычислении их синуса. Зная, что два смежных угла дополнительные, можно утверждать, что sin(угол) = sin(180° - угол) .
Если вы ищете другие формулы площади четырехугольника, воспользуйтесь нашим специальным калькулятором четырехугольника, где вы найдете формулу Бретшнайдера (для четырех сторон и двух противоположных углов) и формулу, в которой используются бимедианы и угол между ними. их.
Формула площади правильного многоугольника
Формула площади правильного многоугольника выглядит следующим образом:
-
Площадь правильного многоугольника = n × a² × cot(π/n) / 4
, где n — количество сторон, а — длина стороны.
Существуют и другие уравнения, в которых используются, например, такие параметры, как радиус описанной окружности или периметр. Вы можете найти эти формулы в специальном параграфе нашего калькулятора площади многоугольника.
Вы можете найти эти формулы в специальном параграфе нашего калькулятора площади многоугольника.
Если вы имеете дело с неправильным многоугольником, помните, что вы всегда можете разделить фигуру на более простые фигуры, например, на треугольники. Просто посчитайте площадь каждого из них и, в конце, просуммируйте их. Разложение многоугольника на множество треугольников называется триангуляцией многоугольника.
Часто задаваемые вопросы
Какой четырехугольник имеет наибольшую площадь?
Для заданного периметра четырехугольник с максимальной площадью всегда будет квадратом .
Какая фигура имеет наибольшую площадь при заданном периметре?
Для заданного периметра замкнутая фигура максимальной площади представляет собой круг .
Как рассчитать площадь неправильной формы?
Чтобы вычислить площадь неправильной формы:
- Разделите фигуру на несколько подформ, для которых можно легко вычислить площадь, например треугольники, прямоугольники, трапеции, (полу)круги и т.
 д.
д. - Вычислите площадь каждой из этих подформ.
- Суммируйте площади подформ, чтобы получить окончательный результат.
Как рассчитать площадь под кривой?
Чтобы найти площадь под кривой на интервале, необходимо вычислить определенный интеграл функции, описывающей эту кривую, между двумя точками, соответствующими концам рассматриваемого интервала.
Ханна Памула, PhD
Площадь круга
Посмотрите 23 похожих калькулятора 2D-геометрии 📏
Площадь прямоугольникаПлощадь полумесяцаЦентр масс… Еще 20
Калькулятор площади 📐 - Рассчитайте площадь квадрата, прямоугольника, треугольника, круга, параллелограмма, трапеции...
Быстрая навигация:
- вычислить площадь любой фигуры?
- Площадь квадрата
- Площадь прямоугольника
- Площадь треугольника
- Площадь круга
- Площадь параллелограмма
- Площадь трапеции
- Площадь эллипса (овала)
- Площадь сектора
- Площадь восьмиугольника
- Где использовать калькулятор площади?
Каждая геометрическая фигура имеет свою формулу для вычисления площади и разные требуемые размеры, которые необходимо знать. См. ниже подробную информацию о каждом отдельном калькуляторе площади, который поддерживает этот калькулятор площади, включая используемую формулу. При выполнении измерений или чтении планов убедитесь, что все измерения указаны в одних и тех же единицах измерения, или преобразуйте их в одни и те же единицы, чтобы получить достоверный результат. Результатом всегда является единица измерения в квадрате, например. квадратные сантиметры, квадратные километры, квадратные дюймы, квадратные футы, квадратные мили...
См. ниже подробную информацию о каждом отдельном калькуляторе площади, который поддерживает этот калькулятор площади, включая используемую формулу. При выполнении измерений или чтении планов убедитесь, что все измерения указаны в одних и тех же единицах измерения, или преобразуйте их в одни и те же единицы, чтобы получить достоверный результат. Результатом всегда является единица измерения в квадрате, например. квадратные сантиметры, квадратные километры, квадратные дюймы, квадратные футы, квадратные мили...
Расчет площади применяется в строительстве и отделке помещений (например, требуется покраска), в управлении земельными ресурсами, сельском хозяйстве, биологии, экологии и многих других дисциплинах.
Площадь квадратаФормула площади квадрата: сторона 2 , как показано на рисунке ниже:
единичное измерение. Однако, поскольку в большинстве практических ситуаций вам нужно измерить обе стороны, прежде чем вы узнаете, что это квадрат, разница может быть невелика, но, по крайней мере, ее легче вычислить.
Площадь прямоугольника
Формула площади прямоугольника: ширина x высота , как показано на рисунке ниже:
и просто умножить их вместе. Это одна из самых простых фигур для вычисления площади. Неправильные формы часто разбивают на ряд прямоугольников, чтобы можно было приблизительно рассчитать их площадь.
Площадь треугольникаФормула площади треугольника: высота x π x (радиус / 2) 2 , где (радиус / 2) - радиус основания (d = 2 x r), так что другой способ записи это высота x π x радиус 2 . Визуально на рисунке ниже:
Несмотря на простоту приведенного выше уравнения, в определенных ситуациях вы можете не знать эти два точных измерения. Существует несколько правил вычисления площади треугольника: SSS (сторона-сторона-сторона), SAS (две стороны и прилежащий угол), SSA (две стороны и не заключенный между ними угол), ASA (два угла и прилежащая сторона). . Для прямоугольных треугольников вы можете вычислить площадь, зная гипотенузу и высоту к ней. Все они поддерживаются этим онлайн-калькулятором площади.
. Для прямоугольных треугольников вы можете вычислить площадь, зная гипотенузу и высоту к ней. Все они поддерживаются этим онлайн-калькулятором площади.
Площадь круга
Формула площади круга: π x радиус 2 , но диаметр круга равен d = 2 x r, поэтому его можно записать по-другому: π х (диаметр / 2) 2 . Визуально на рисунке ниже:
Для площади круга вам нужен только его радиус. В большинстве практических ситуаций было бы проще рассчитать диаметр, поэтому наш калькулятор использует диаметр в качестве входных данных.
Площадь параллелограммаФормула площади параллелограмма равна ширина x высота , как показано на рисунке ниже: к прямоугольнику для вычисления площади, таким образом, формула в основном такая же, но мы используем высоту параллелограмма вместо его стороны.
Площадь трапеции
Формула площади трапеции: (основание 1 + основание 2) / 2 x высота , как показано на рисунке ниже:
особенно с помощью калькулятора площади.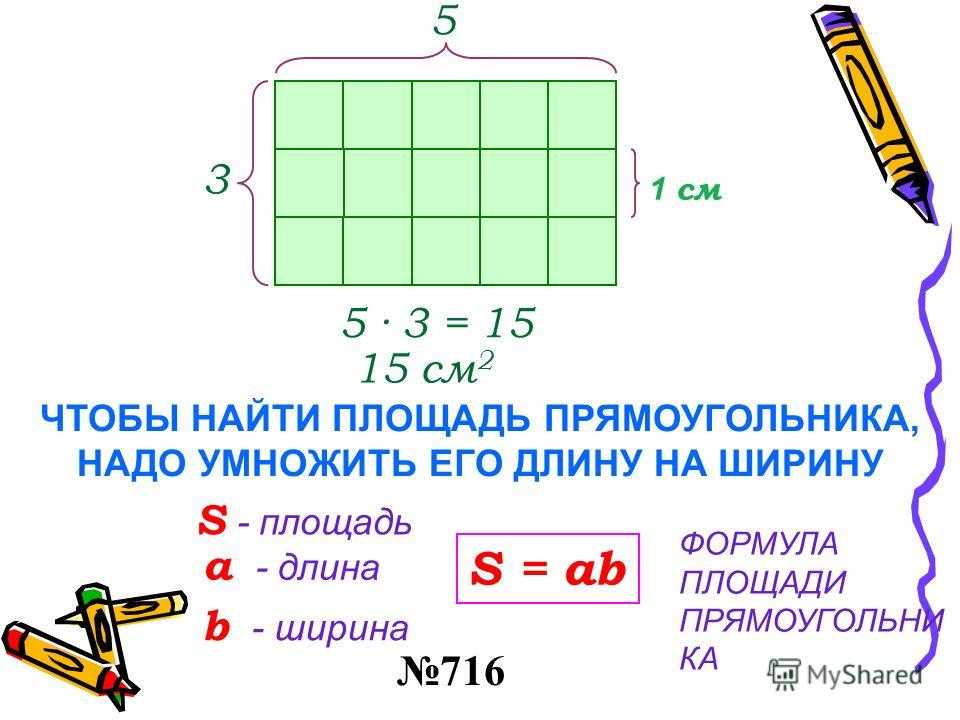 Трапецию можно преобразовать в прямоугольник, зная длину каждого основания и его высоту, так что это минимальные необходимые измерения.
Трапецию можно преобразовать в прямоугольник, зная длину каждого основания и его высоту, так что это минимальные необходимые измерения.
Формула площади эллипса: π x большой радиус x малый радиус , как показано на рисунке ниже:
Площадь овала аналогична площади круга, но поскольку у него два радиуса, немного отличается. Здесь вы можете измерить два диаметра и разделить на два, чтобы получить два радиуса.
Площадь сектора
Формула площади сектора: (угол / 360) x π x радиус , но диаметр круга равен d = 2 x r, так что другой способ записи (угол / 360) 2 x π x (диаметр / 2) . Визуально на рисунке ниже:
Поскольку сектор — это просто срез круга, формула очень похожа на формулу для площади круга, с той разницей, которая необходима для расчета того, какую часть круга покрывает сектор. В то время как радиус легко измерить, угол — нет, если только у вас нет под рукой надлежащего инструмента, который может быть необходимым условием для использования нашего калькулятора площади.

