кубатурник
производство пиломатериала
Главная > кубатурник
Используя данную таблицу, Вы всегда с легкостью сможете перевести штуки в кубы и обратно, узнать сколько штук бруса или доски в кубе, вес, объём, количество погонных метров в кубе. В таблице приведены основные размеры изделий.
Наименование |
размер, мм |
Кол-во штук в одном м3 |
Кол-во погонных метров в одном м3 |
Объём одной доски, бруса м3 |
Площадь одной доски, кв. |
Вес. штуки в кг (влажн. 20%) |
Доска обрезная |
100*25*6000 |
66,7 |
|
0,015 |
0,6 |
11,25 |
Доска обрезная |
100*25*3000 |
|
400 |
0,0075 |
0,3 |
5,625 |
Доска обрезная | 100*25*4000 |
100 |
400 |
0,01 |
0,4 |
7,5 |
Доска обрезная |
100*25*5000 |
80 |
400 |
0,0125 |
0,5 |
9,375 |
Доска заборная |
100*25*2000 |
200 |
400 |
0,005 |
|
3,75 |
Доска обрезная |
150*25*6000 |
44,4 |
266,4 | 0,0225 |
0,9 |
16,875 |
Доска обрезная |
150*25*3000 |
88,9 |
266,8 |
0,01125 |
0,45 |
8,44 |
Доска обрезная |
150*25*4000 |
66,7 |
266,8 |
0,015 |
0,6 |
11,24 |
Доска обрезная |
150*25*5000 |
44,4 |
222,2 |
0,0225 |
0,75 |
16,9 |
Доска заборная |
150*25*2000 |
133,3 |
266,7 |
0,0075 |
0,3 |
5,625 |
Доска обрезная |
200*25*6000 |
33,3 |
200 |
0,03 |
1,2 |
22,5 |
Доска обрезная |
100*32*6000 |
52,1 |
312,5 |
0,0192 |
0,6 |
14,4 |
Доска обрезная |
150*32*6000 |
34,7 |
208,3 |
0,0288 |
0,9 |
21,6 |
Доска обрезная |
100*40*6000 | 41,7 |
250 | 0,024 | 0,6 | 18 |
Доска обрезная |
150*40*6000 |
27,8 | 166,7 | 0,036 | 0,9 | 27 |
Доска обрезная |
180*40*6000 |
23,1 | 138,6 |
0,0432 |
1,08 |
32,46 |
Доска обрезная | 200*40*6000 | 20,8 | 125 | 0,048 | 1,2 | 36 |
Доска обрезная |
100*50*6000 |
33,3 |
200 |
0,03 |
0,6 |
22,5 |
Доска обрезная | 150*50*6000 | 22,2 | 133,3 | 0,045 | 0,9 | 33,75 |
Доска обрезная |
|
18,5 |
111,1 |
0,054 |
1,08 |
40,54 |
Доска обрезная |
200*50*6000 |
16,7 |
100 |
0,06 |
1,2 |
45 |
Брус | 50*50*6000 | 66,67 | 400 | 0,015 | — | 11,25 |
Брус | 40*40*6000 | 104,1 | 625 | 0,0096 | — | 7,2 |
Брус | 100*100*6000 | 16,67 | 100 | 0,06 | — | 45 |
Брус | 150*100*6000 | 11,11 | 66,67 | 0,09 | — | 67,5 |
Брус | 200*100*6000 | 8,33 | 50 | 0,12 | — | 90 |
Брус | 150*150*6000 | 7,41 | 44,44 | 0,135 | — | 101,25 |
Брус | 180*180*6000 | 5,15 | 30,9 | 0,194 | — | 145,6 |
Брус | 200*200*6000 | 4,17 | 25 | 0,24 | — | 180 |
Брус | 200*180*6000 | 4,63 | 27,78 | 0,216 | — | 162 |
Брус | 200*150*6000 | 5,56 | 33,3 | 0,18 | — | 134,9 |
Брус | 180*100*6000 | 9,26 | 55,5 | 0,108 | — | 81 |
Брус | 180*150*6000 | 6,17 | 37 | 0,162 | — | 121,6 |
Брус | 75*75*6000 | 29,4 | 176,5 | 0,034 | — | 25,5 |
Расчёт кубатуры досок, бруса — онлайн калькулятор
Скачать, сохранить результат
Вы можете сохранить результат расчёта в формате PDF на ваше устройство, выбрав «Сохранить как PDF» в окне печати.
 Либо просто распечатайте результаты на бумагу.
Либо просто распечатайте результаты на бумагу.
Пиломатериалы – являются одним из самых востребованных материалов для строительства на данный момент. Сфера применения просто огромна. Непосредственно в стройке, пиломатериал используется практически на каждой стадии, он входит в полный цикл общестроительных работ, от опалубки фундамента, до несущих конструкций на кровлю. Данный вид материала очень неприхотлив в использовании, что делает работу с ним, незаменимой и приятой.
Лес является незаменимым строительным и отделочным материалом на протяжении всей истории человечества, поскольку обладает доступностью, прочностью, природной красотой и, что не мало важно в последнее время, экологичностью. Пиломатериалы – это обработанный продукт распила древесины хвойных и лиственных пород, который в зависимости от назначения имеет прямоугольную (брус, доска, вагонка), круглую форму сечения (бревно) или смешанную (лафет, горбыль, шпала).
Практически весь сортамент пиломатериалов, представленный на рынке, отпускается по объему (м3) и соответственно, цена указана за 1 м3, однако хоть и намного реже, но встречается продажа за единицу площади (м2), например, вагонки или террасной доски.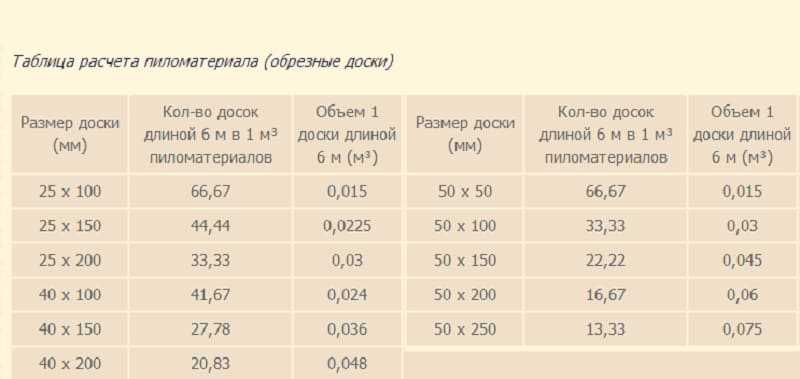 Для того чтобы понять, какое количество материалов потребуется для выполнения поставленных работ, необходимо рассчитать кубатуру одной единицы леса и узнать сколько его содержится в отпускаемой партии.
Для того чтобы понять, какое количество материалов потребуется для выполнения поставленных работ, необходимо рассчитать кубатуру одной единицы леса и узнать сколько его содержится в отпускаемой партии.
Особенности расчета пиломатериалов:
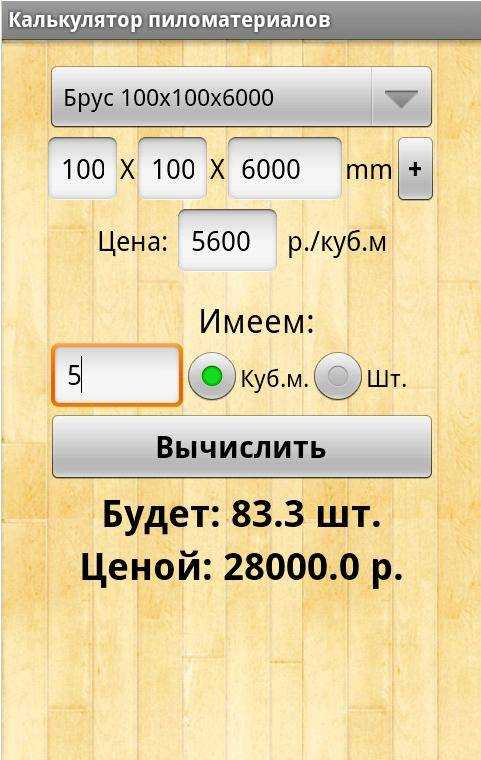
Данный калькулятор пиломатериалов помогает быстро произвести расчет из шт в м3 и наоборот. Для расчета необходимо указать длину доски или бруса в миллиметрах (S1). Ширину и толщину (S2/S3), так же при необходимости вы сразу можете узнать стоимость рассчитываемого пиломатериала, заполнив соответствующее поле. Стоимость леса можете уточнить у любого поставщика в своем районе, или на ближайшем строительном рынке. Обычно цену указывают за кубический метр, и тут незаменимую роль сыграет данный скрипт для расчета. Ведь согласитесь высчитать стоимость нескольких досок, когда вам говорят стоимость за куб, достаточно проблематично.
Освоив данный кубатурник пиломатериала, перед вами больше не будет стоять вопрос, как посчитать пиломатериал. Доверьте рутинный расчет, калькулятору пиломатериала, и вы не только сэкономите свое личное время, но и исключите ошибки в расчетах, что точно приведет вас к экономии средств.
Доверьте рутинный расчет, калькулятору пиломатериала, и вы не только сэкономите свое личное время, но и исключите ошибки в расчетах, что точно приведет вас к экономии средств.
Какие виды пиломатериала бывают
- Обрезная доска, пожалуй, один из самых востребованных материалов на рынке строительных материалов. Такой вид материала используется повсюду, при строительстве домов, бань, подсобных помещений, отдельных конструктивных элементов, таких как лестницы, заборы, окна, двери, крыши и так далее. Расчёт кубатуры досок в кубе вам поможет произвести наша специально разработанная программа. Сохраняйте данную страницу в закладках, и вы всегда, быстро и удобно, сможете произвести расчет любой древесины.
- Брус, это продукт пиломатериалов прямоугольного или квадратного сечения, так же как и доска имеет обширное применение не только на строительном рынке, но и в мебельном производстве. Покупая этот материал легко попасть на уловки недобросовестных продавцов. Помимо его влажности, четких габаритных размеров, класса и качества, хитрые менеджеры с легкостью могут обсчитать вас на общем объеме.
 А вы знаете, как правильно произвести расчет кубатуры бруса? Просто воспользуйтесь данным онлайн калькулятором пиломатериалов кубатуры, и сэкономьте свои нервы и деньги.
А вы знаете, как правильно произвести расчет кубатуры бруса? Просто воспользуйтесь данным онлайн калькулятором пиломатериалов кубатуры, и сэкономьте свои нервы и деньги.
Смотрите также:
НЕКОТОРЫЕ НОВЫЕ И ЭФФЕКТИВНЫЕ ПРОИЗВОДНЫЕ СХЕМЫ ДЛЯ ЧИСЛЕННОЙ КУБАТУРЫ – Журнал
админ 28 октября 2020 г.
Авторы:
Камран Малик, Мухаммад Муджтаба Шейх, Мухаммад Салим Чандио, Абдул Васим Шейх,
DOI NO:
https://doi.org/10.26782/jmcms.2020.10.00005
Кубатура, Двойные интегралы, Производные схемы, Точность, Порядок точности, Трапеция,
Abstract
В этой исследовательской работе были предложены некоторые новые численные кубатурные схемы на основе производных для точного вычисления двойных интегралов в конечном диапазоне. Предлагаемые модификации основаны на квадратурных и кубатурных правилах трапециевидного типа.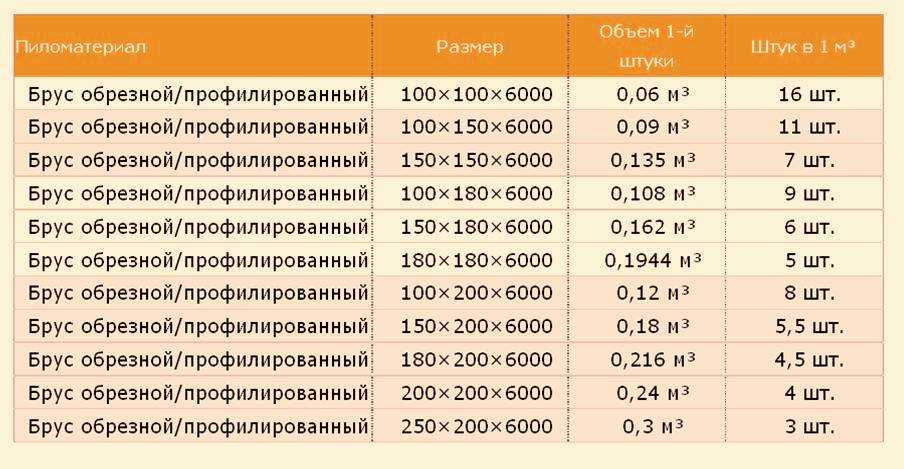 Предлагаемые схемы важны для численного вычисления сложных двойных интегралов, где точное значение недоступно, а можно получить только приближенные значения. Предлагаемые схемы двойного интеграла на основе производной обеспечивают эффективные результаты в отношении более высокой точности и порядка точности. Предлагаемые схемы в базовой и составной формах с локальными и глобальными погрешностями представлены с необходимыми доказательствами с оценкой их производительности по обычному правилу трапеций с помощью некоторых численных экспериментов. Последующие наблюдаемые распределения ошибок предложенных схем оказались ниже, чем у традиционной трапециевидной кубатурной схемы в составной форме
Предлагаемые схемы важны для численного вычисления сложных двойных интегралов, где точное значение недоступно, а можно получить только приближенные значения. Предлагаемые схемы двойного интеграла на основе производной обеспечивают эффективные результаты в отношении более высокой точности и порядка точности. Предлагаемые схемы в базовой и составной формах с локальными и глобальными погрешностями представлены с необходимыми доказательствами с оценкой их производительности по обычному правилу трапеций с помощью некоторых численных экспериментов. Последующие наблюдаемые распределения ошибок предложенных схем оказались ниже, чем у традиционной трапециевидной кубатурной схемы в составной форме
Ссылка:
И. А. Харшавардхан, Сайед Наваз Паша, Саллауддин Мд, Д. Рамеш, «МЕТОДЫ, ИСПОЛЬЗУЕМЫЕ ДЛЯ КЛАСТЕРИЗАЦИИ ДАННЫХ И ИНТЕГРАЦИИ КЛАСТЕРНОГО АНАЛИЗА В РАМКАХ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ», J.Mech.Cont.& Math. наук, т.-14, №-6, ноябрь-декабрь (2019) стр. 546-557
II. Баболиан Э., М. Масджед-Джамей и М. Р. Эслахчи, О численном улучшении квадратурных правил Гаусса-Лежандра, Прикладная математика и вычисления, 160 (2005) 779-789.
Баболиан Э., М. Масджед-Джамей и М. Р. Эслахчи, О численном улучшении квадратурных правил Гаусса-Лежандра, Прикладная математика и вычисления, 160 (2005) 779-789.
III. Бейли Д. Х. и Борвейн Дж. М., «Высокоточное численное интегрирование: прогресс и проблемы», Журнал символических вычислений, том. 46, нет. 7, стр. 741–754, 2011.
IV. Бхатти, А.А., М.С. Чандио, Р.А. Мемон и М.М. Шейх, (2019), «Модифицированный алгоритм уменьшения ошибки при комбинированном численном интегрировании», Исследовательский журнал Университета Синда-SURJ (Science Series) 51 (4): 745-750.
В. Берден Р. Л., Дж. Д. Файрес, Численный анализ, Брукс/Коул, Бостон, Массачусетс, США, 9-е издание, 2011 г.
VI. Бург. COE, Замкнутая числовая квадратура Ньютона-Котеса на основе производных, Прикладная математика и вычисления, 218 (2012), 7052-7065.
VII. Дехган М., М. Масджед-Джамей и М. Р. Эслахчи, Полуоткрытое квадратурное правило Ньютона-Котеса и его численное усовершенствование, Прикладная математика и вычисления, 171 (2005) 1129-1140.
VIII. Деган М., Масджед-Джамей М., Эслахчи М. Р. О численном улучшении замкнутых квадратурных правил Ньютона-Котеса // Прикладная математика и вычисления. 165, нет. 2, стр. 251–260, 2005.
IX. Дехган М., М. Масджед-Джамей и М. Р. Эслахчи, «О численном улучшении открытых квадратурных правил Ньютона-Котеса», Прикладная математика и вычисления, том. 175, нет. 1, pp.618–627, 2006.
X. Jain M.K., S.R.K. Iyengar and R.K. Jain, Numerical Methods for Scientific and Computation, New Age International (P) Limited, Fifth Edition, 2007.
XI. Мемон К., М.М. Шайх, М.С. Чандио, А.В. Шайх, «Модифицированная схема на основе производной для интеграла Римана-Стилтьеса», 52(01) 37-40 (2020).
XII. МОХАММЕД М. Файяд, Р. Кандасами, РАДИЯ Мохаммед, ДЖААФАР Абдул Аббас Аббуд, «ЭФФЕКТИВНОСТЬ сырой нефти Al2O3 НА НЕЛИНЕЙНОМ РАСТЯЖЕНИИ ЛИСТ», J. Mech. продолжение и математика. наук, Т.-13, №-5, ноябрь-декабрь (2018) С. 263-279
XIII. Пал М., Численный анализ для ученых и инженеров: теория и программы C, Alpha Science, Оксфорд, Великобритания, 2007.
XIV. Петровская Н., Вентурино Э., «Численное интегрирование данных с разреженной выборкой», Практика и теория имитационного моделирования, том. 19, нет. 9, стр. 1860–1872, 2011.
XV. Рамачандран Т. (2016), Д. Удаякумар и Р. Паримала, «Сравнение среднего арифметического, среднего геометрического и среднего гармонического производного на основе замкнутой квадратуры Ньютона-Котеса», Nonlinear Dynamics and Chaos Vol. 4, № 1, 2016, 35-43 ISSN: 2321 – 9238.
XVI. Шастри С.С., Введение в методы численного анализа, Prentice-Hall of India, 19.97.
XVII. Шайх, М.М., (2019), «Анализ методов полиномиальной коллокации и равномерно распределенных квадратур для линейных интегральных уравнений Фредгольма второго рода – сравнение». Турецкий журнал анализа и теории чисел, 7 (4) 91–97. doi: 10.12691/tjant-7-4-1.
XVIII. Шейх, М.М., М.С. Чандио и А.С. Соомро, (2016), «Модифицированное четырехточечное квадратурное правило с закрытой средней точкой для численного интегрирования», Исследовательский журнал Университета Синд-SURJ (Science Series) 48 (2): 389-392.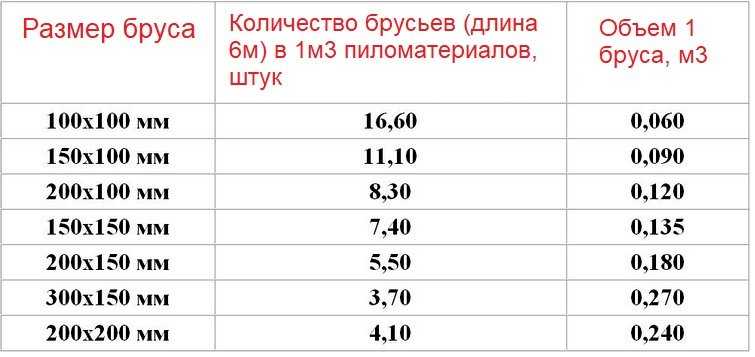
XIX. Зафар Ф., С. Салим и К.О.Э. Бург, Новая производная на основе открытых квадратурных правил Ньютона-Котеса, Абстрактный и прикладной анализ, том 2014 г., идентификатор статьи 109138, 16 страниц, 2014 г.
XX. Чжао, В. и Х. Ли, (2013) «Замкнутая квадратура Ньютона-Котеса на основе производной средней точки», Аннотация и прикладной анализ, ID статьи 492507.
XXI. Чжао, В., З. Чжан и З. Е, (2014), «Правило трапеций на основе производной средней точки для интеграла Римана-Стилтьеса», Итальянский журнал чистой и прикладной математики, 33: 369-376.
ПосмотретьСкачать


 м.
м. Кубатурная фильтрация Калмана для непрерывно-дискретных систем: теория и моделирование [J]. IEEE Transactions on Signal Processing, 2010, 58(10): 49.77-4993. doi: 10.1109/TSP.2010.2056923
Кубатурная фильтрация Калмана для непрерывно-дискретных систем: теория и моделирование [J]. IEEE Transactions on Signal Processing, 2010, 58(10): 49.77-4993. doi: 10.1109/TSP.2010.2056923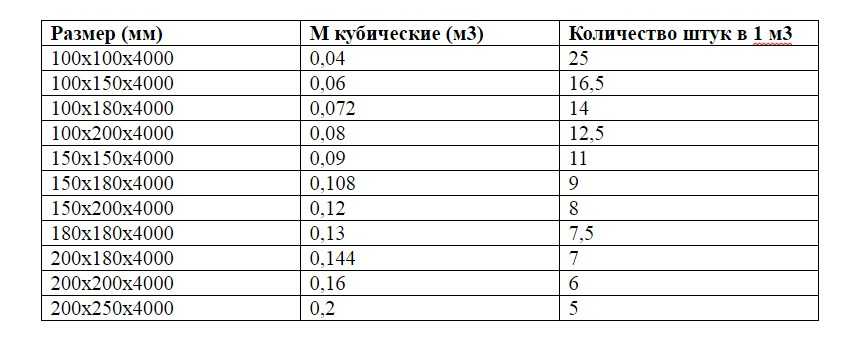 Китайский журнал аэронавтики, 2019 г., 32(11): 2489-2502. doi: 10.1016/j.cja.2019.07.025
Китайский журнал аэронавтики, 2019 г., 32(11): 2489-2502. doi: 10.1016/j.cja.2019.07.025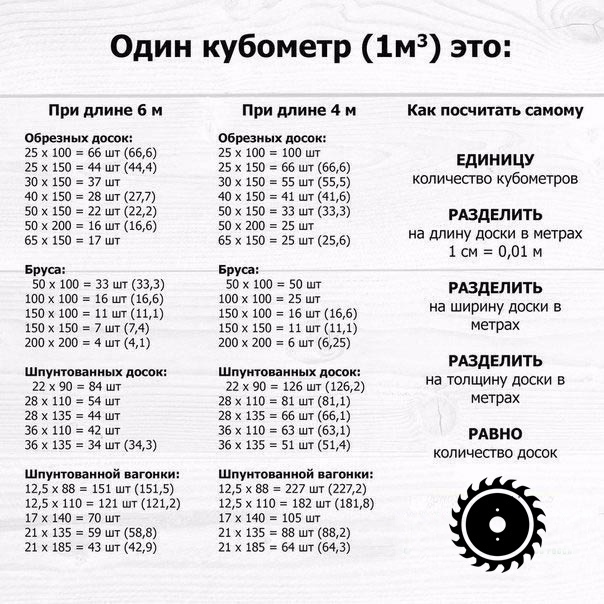 дои: 10.1109/ДОСТУП.2018.2808170
дои: 10.1109/ДОСТУП.2018.2808170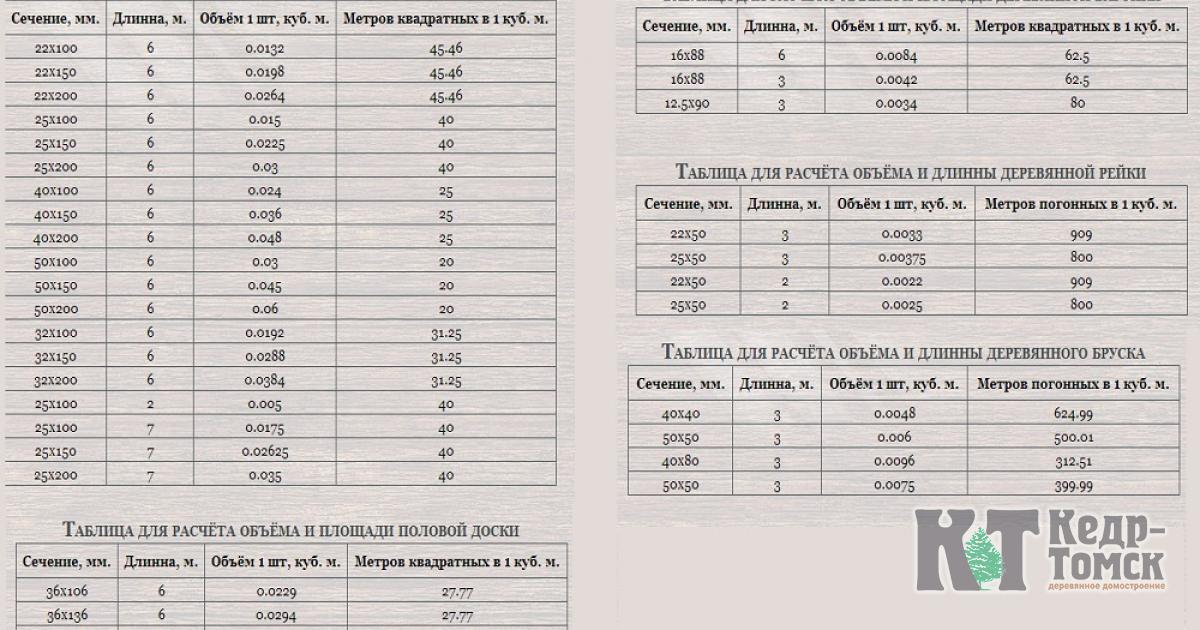 Подходы к адаптивной фильтрации[J]. IEEE Transactions on Automatic Control, 1972, 17(5): 693-698. doi: 10.1109/TAC.1972.1100100
Подходы к адаптивной фильтрации[J]. IEEE Transactions on Automatic Control, 1972, 17(5): 693-698. doi: 10.1109/TAC.1972.1100100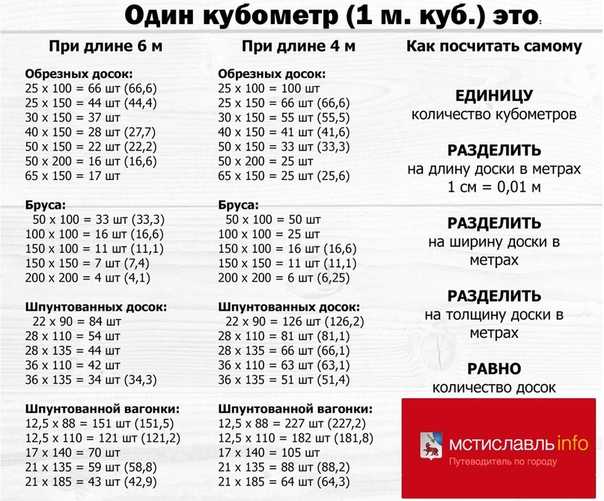 Пискатауэй: IEEE Press, 2014: 16-20.
Пискатауэй: IEEE Press, 2014: 16-20.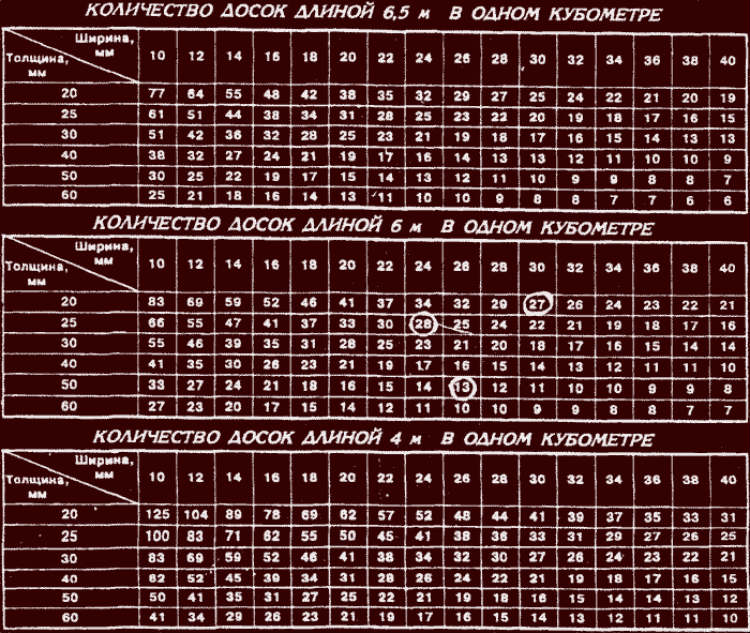 Журнал Пекинского университета аэронавтики и астронавтики, 2022 г., 48(4): 716-724 (на китайском языке).
Журнал Пекинского университета аэронавтики и астронавтики, 2022 г., 48(4): 716-724 (на китайском языке).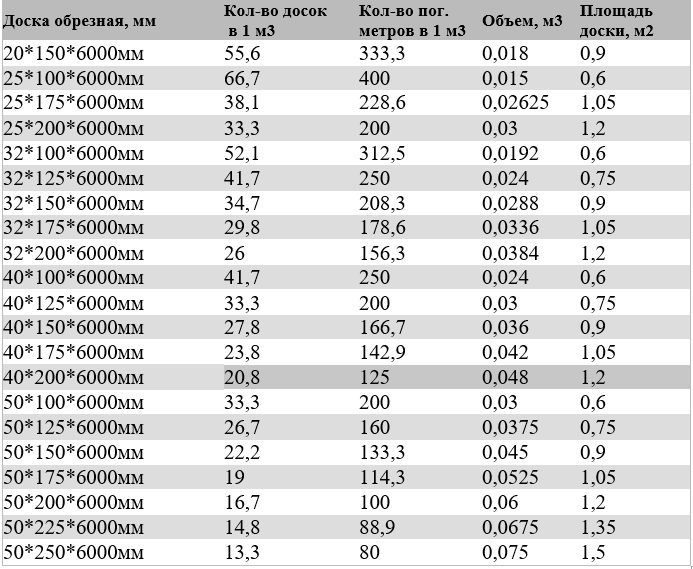
 Адаптивная навигация и кинематическое позиционирование[M]. Пекин: Surveying and Mapping Press, 2006: 9.5-97.
Адаптивная навигация и кинематическое позиционирование[M]. Пекин: Surveying and Mapping Press, 2006: 9.5-97. дои: 10.2514/1.G000257
дои: 10.2514/1.G000257