- Калькулятор балок – основные расчеты для перекрытий и стропил + видео
- Калькулятор расчета металлической двутавровой балки на прогиб, прочность
- Онлайн калькулятор для расчета желебобетонных балок перекрытия дома
- Балки под сосредоточенной нагрузкой | Онлайн калькулятор
- Калькулятор балок. Расчет нагрузки на балки перекрытия. Нагрузка на балку: нюансы
- Расчёт железобетонной балки
- Калькулятор подбора деревянных двутавровых балок
- Бесплатный калькулятор луча | Калькулятор изгибающего момента, поперечной силы и прогиба
- | SkyCiv
- Калькулятор нагрузки на балку
- Калькулятор деревянных балок | Какой размер мне нужен?
- Балки — поддерживаются с обеих сторон
- 00 psi
- 00 фунтов / дюйм
- 00 psi
- 00 фунтов / дюйм
- Нагрузки на балку — Калькулятор опорной силы
- Простой калькулятор балок | calcresource
- Предпосылки
- Введение
- Балка с простой опорой и равномерно распределенной нагрузкой
- Балка с простой опорой и точечной силой в середине
- Балка с простой опорой, с точечной силой в произвольном положении
- Балка с простой опорой с точечным моментом
- Балка с простой опорой и треугольной нагрузкой
- Балка с простой опорой и трапецеидальной нагрузкой
- Балка с простой опорой и трапециевидным распределением нагрузки типа плиты
- Балка с простой опорой и частично распределенной равномерной нагрузкой
- Балка с простой опорой и частично распределенной трапециевидной нагрузкой
- Предпосылки
Калькулятор балок – основные расчеты для перекрытий и стропил + видео
Балки в доме относятся обычно к стропильной системе или перекрытию, и, чтобы получить надежную конструкцию, эксплуатация которой может осуществляться без каких-либо опасений, необходимо использовать калькулятор балок.
На чем строится калькулятор балок
Когда стены уже подведены под второй этаж или под крышу, необходимо сделать перекрытие, во втором случае плавно переходящее в стропильные ноги. При этом материалы нужно подобрать так, чтобы и нагрузка на кирпичные либо бревенчатые стены не превышала допустимую, и прочность конструкции была на должном уровне. Следовательно, если вы собираетесь использовать древесину, нужно правильно подобрать балки из нее, сделать расчеты для выяснения нужной толщины и достаточной длины.
Калькулятор балок
Укажите размеры балок перекрытий и шаг.Проседанию или частичному разрушению перекрытия могут послужить разные причины, например, слишком большой шаг между лагами, прогиб поперечин, слишком малая площадь их сечения или дефекты в структуре. Чтобы исключить возможные эксцессы, следует выяснить предполагаемую нагрузку на перекрытие, будь оно цокольное или межэтажное, после чего используем калькулятор балок, учитывая их собственную массу. Последняя может меняться в бетонных перемычках, вес которых зависит от плотности армирования, для дерева и металла при определенной геометрии масса постоянна. Исключением бывает отсыревшая древесина, которую не используют в строительных работах без предварительной сушки.
Чтобы исключить возможные эксцессы, следует выяснить предполагаемую нагрузку на перекрытие, будь оно цокольное или межэтажное, после чего используем калькулятор балок, учитывая их собственную массу. Последняя может меняться в бетонных перемычках, вес которых зависит от плотности армирования, для дерева и металла при определенной геометрии масса постоянна. Исключением бывает отсыревшая древесина, которую не используют в строительных работах без предварительной сушки.
На балочные системы в перекрытиях и стропильных конструкциях оказывают нагрузку силы, действующие на изгиб сечения, на кручение, на прогиб по длине. Для стропил также нужно предусмотреть снеговую и ветровую нагрузку, которые также создают определенные усилия, прилагаемые к балкам. Также нужно точно определить необходимый шаг между перемычками, поскольку слишком большое количество поперечин приведет к лишней массе перекрытия (или кровли), а слишком малое, как было сказано выше, ослабит конструкцию.
Вам также может быть интересна статья о расчёте количества необрезной и обрезной доски в кубе: https://remoskop.
ru/kolichestvo-dosok-v-kube.html
Как рассчитать нагрузку на балку перекрытия
Расстояние между стенами называется пролетом, и в помещении их насчитывается два, причем один пролет обязательно будет меньше другого, если форма комнаты не квадратная. Перемычки межэтажного или чердачного перекрытия следует укладывать по более короткому пролету, оптимальная длина которого – от 3 до 4 метров. При большем расстоянии могут потребоваться балки нестандартных размеров, что приведет к некоторой зыбкости настила. Оптимальным выходом в этом случае будет использование металлических поперечин.
Что касается сечения деревянного бруса, есть определенный стандарт, требующий, чтобы стороны балки соотносились как 7:5, то есть высота делится на 7 частей, и 5 из них должны составить ширину профиля. В этом случае деформация сечения исключается, если же отклониться от вышеуказанных показателей, то при ширине, превышающей высоту, получится прогиб, либо, при обратном несоответствии – загиб в сторону. Чтобы подобное не получилось из-за чрезмерной длины бруса, нужно знать, как рассчитать нагрузку на балку. В частности, допустимый прогиб вычисляется из соотношения к длине перемычки, как 1:200, то есть должен составлять 2 сантиметра на 4 метра.
Чтобы подобное не получилось из-за чрезмерной длины бруса, нужно знать, как рассчитать нагрузку на балку. В частности, допустимый прогиб вычисляется из соотношения к длине перемычки, как 1:200, то есть должен составлять 2 сантиметра на 4 метра.
Чтобы брус не провисал под тяжестью лагов и настила, а также предметов интерьера, можно выточить его снизу на несколько сантиметров, придав форму арки, в этом случае его высота должна иметь соответствующий запас.
Теперь обратимся к формулам. Тот же прогиб, о котором говорилось ранее, рассчитывается так: fнор = L/200, где L – длина пролета, а 200 – допустимое расстояние в сантиметрах на каждую единицу проседания бруса. Для железобетонной балки, распределенная нагрузка q на которую обычно приравнивается 400 кг/м2, расчет предельного изгибающего момента выполняется по формуле Мmax = (q · L2)/8. При этом количество арматуры и ее вес определяется по следующей таблице:
Площади поперечных сечений и масса арматурных стержней
Диаметр, мм | Площадь поперечного сечения, см2, при числе стержней | Масса 1 пог. | Диаметр, мм | ||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
Проволочная и стержневая арматура | |||||||||||
3 | 0.071 | 0.141 | 0.212 | 0.283 | 0.353 | 0.424 | 0.5 | 0.565 | 0.636 | 0.052 | 3 |
4 | 0.126 | 0.25 | 0. | 0.5 | 0.68 | 0.75 | 0.88 | 1 | 1.18 | 0.092 | 4 |
5 | 0.196 | 0.39 | 0.59 | 0.79 | 0.98 | 1.18 | 1.38 | 1.57 | 1.77 | 0.154 | 5 |
6 | 0.283 | 0.57 | 0.85 | 1.13 | 1.42 | 1.7 | 1.98 | 2. | 2.55 | 0.222 | 6 |
7 | 0.385 | 0.77 | 1.15 | 1.54 | 1.92 | 2.31 | 2.69 | 3.08 | 3.46 | 0.302 | 7 |
8 | 0.503 | 1.01 | 1.51 | 2.01 | 2.52 | 3.02 | 3.52 | 4.02 | 4.58 | 0.395 | 8 |
9 | 0. | 1.27 | 1.91 | 2.54 | 3.18 | 3.82 | 4.45 | 5.09 | 5.72 | 0.499 | 9 |
10 | 0.785 | 1.57 | 2.36 | 3.14 | 3.93 | 4.71 | 5.5 | 6.28 | 7.07 | 0.617 | 10 |
12 | 1.131 | 2.26 | 3.39 | 4.52 | 5.65 | 6. | 7.91 | 9.04 | 10.17 | 0.888 | 12 |
14 | 1.539 | 3.08 | 4.61 | 6.15 | 7.69 | 9.23 | 10.77 | 12.3 | 13.87 | 1.208 | 14 |
16 | 2.011 | 4.02 | 6.03 | 8.04 | 10.05 | 12.06 | 14.07 | 16.08 | 18.09 | 1. | 16 |
18 | 2.545 | 5.09 | 7.63 | 10.17 | 12.7 | 15.26 | 17.8 | 20.36 | 22.9 | 1.998 | 18 |
20 | 3.142 | 6.28 | 9.41 | 12.56 | 15.7 | 18.84 | 22 | 25.13 | 28.27 | 2.465 | 20 |
22 | 3.801 | 7. | 11.4 | 15.2 | 19 | 22.81 | 26.61 | 30.41 | 34.21 | 2.984 | 22 |
25 | 4.909 | 9.82 | 14.73 | 19.64 | 24.54 | 29.45 | 34.36 | 39.27 | 44.18 | 3.85 | 25 |
28 | 6.153 | 12.32 | 18.47 | 24.63 | 30.79 | 36. | 43.1 | 49.26 | 55.42 | 4.83 | 28 |
32 | 8.043 | 16.09 | 24.18 | 32.17 | 40.21 | 48.26 | 56.3 | 64.34 | 72.38 | 6.31 | 32 |
36 | 10.179 | 20.36 | 30.54 | 40.72 | 50.89 | 61.07 | 71.25 | 81.43 | 91.61 | 7. | 36 |
40 | 12.561 | 25.13 | 37.7 | 50.27 | 62.83 | 75.4 | 87.96 | 100.53 | 113.1 | 9.865 | 40 |
45 | 15.904 | 31.81 | 47.71 | 63.62 | 79.52 | 95.42 | 111.33 | 127.23 | 148.13 | 12.49 | 45 |
50 | 19.635 | 39. | 58.91 | 78.54 | 98.18 | 117.81 | 137.45 | 157.08 | 176.72 | 15.41 | 50 |
55 | 23.76 | 47.52 | 71.28 | 95.04 | 118.8 | 142.56 | 166.32 | 190.08 | 213.84 | 18.65 | 55 |
60 | 28.27 | 56.54 | 84.81 | 113.08 | 141.35 | 169. | 197.89 | 226.16 | 254.43 | 22.19 | 60 |
70 | 38.48 | 76.96 | 115.44 | 153.92 | 192.4 | 220.88 | 269.36 | 307.84 | 346.32 | 30.21 | 70 |
80 | 50.27 | 100.54 | 150.81 | 201.08 | 251.35 | 301.62 | 351.89 | 402.16 | 452.43 | 39. | 80 |
Семипроволочные канаты класса К-7 | |||||||||||
4.5 | 0.127 | 0.25 | 0.38 | 0.51 | 0.64 | 0.76 | 0.89 | 1.01 | 1.14 | 0.102 | 4.5 |
6 | 0.226 | 0.45 | 0.68 | 0.9 | 1.13 | 1.36 | 1.58 | 1.81 | 2.03 | 0.181 | 6 |
7. | 0.354 | 0.71 | 1.06 | 1.41 | 1.77 | 2.12 | 2.48 | 2.83 | 3.18 | 0.283 | 7.5 |
9 | 0.509 | 1.02 | 1.53 | 2.04 | 2.54 | 3.05 | 3.56 | 4.07 | 4.58 | 0.407 | 9 |
12 | 0.908 | 1.82 | 2.72 | 3.63 | 4.54 | 5.45 | 6.35 | 7.26 | 8.17 | 0.724 | 12 |
15 | 1.415 | 2.83 | 4.24 | 5.66 | 7.07 | 8.49 | 9.9 | 11.32 | 12.73 | 1.132 | 15 |
Нагрузка на любую балку из достаточно однородного материала рассчитывается по ряду формул. Для начала высчитывается момент сопротивления W ≥ М/R. Здесь М – это максимальный изгибающий момент прилагаемой нагрузки, а R – расчетное сопротивление, которое берется из справочников в зависимости от используемого материала. Поскольку чаще всего балки имеют прямоугольную форму, момент сопротивления можно рассчитать иначе: Wz = b · h2 /6, где b является шириной балки, а h – высотой.
Что еще следует знать про нагрузки на балку
Перекрытие, как правило, является заодно и полом следующего этажа и потолком предыдущего. А значит, нужно сделать его таким, чтобы не было риска объединить верхние и нижние помещения путем банального перегруза меблировкой. Особенно такая вероятность возникает при слишком большом шаге между балками и отказе от лагов (дощатые полы настилаются прямо на брус, уложенный в пролеты). В этом случае расстояние между поперечинами напрямую зависит от толщины досок, например, если она составляет 28 миллиметров, то длина доски не должна быть более 50 сантиметров. При наличии лагов минимальный промежуток между балками может достигать 1 метра.
Также обязательно следует учитывать массу утеплителя, используемого для пола. Например, если укладываются маты из минеральной ваты, то квадратный метр цокольного перекрытия будет весить от 90 до 120 килограммов, в зависимости от толщины термоизоляции. Опилкобетон увеличит массу такого же участка в два раза. Использование же керамзита сделает перекрытие еще тяжелее, поскольку на квадратный метр будет приходиться нагрузка в 3 раза больше, чем при укладке минеральной ваты. Далее, не следует забывать про полезную нагрузку, которая для межэтажных перекрытий составляет 150 килограммов на квадратный метр минимум. На чердаке достаточно принять допустимую нагрузку в 75 килограммов на квадрат.
Оцените статью: Поделитесь с друзьями!Калькулятор расчета металлической двутавровой балки на прогиб, прочность
A1 6 ммА1 8 ммA1 10 ммА1 12 ммА1 14 ммА1 16 ммА1 18 ммА1 20 ммА3 35ГС 6 ммА3 35ГС 8 ммА3 35ГС 10 ммА3 35ГС 12 ммА3 35ГС 14 ммА3 35ГС 16 ммА3 35ГС 18 ммА3 35ГС 20 ммА3 35ГС 22 ммА3 35ГС 25 ммА3 35ГС 28 ммА3 35ГС 32 ммА3 35ГС 36 ммА3 25Г2С 8 ммА3 25Г2С 10 ммА3 25Г2С 12 ммА3 25Г2С 14 ммА3 25Г2С 16 ммА3 25Г2С 18 ммА3 25Г2С 20 ммА3 25Г2С 22 ммА3 25Г2С 25 ммА3 25Г2С 28 ммА3 25Г2С 32 ммА3 25Г2С 36 ммA500С 8 ммA500С 10 ммA500С 12 ммA500С 14 ммA500С 16 ммA500С 18 ммA500С 20 ммA500С 22 ммA500С 25 ммА500С 28 ммA500С 32 ммA500С 36 ммA500С 40 ммA400С 8 ммA400С 10 ммA400С 12 ммАт800 12 ммАт800 14 мм10, г/к12, г/к14, г/к16, г/к18, г/к20, г/к30, г/к36, г/к45, г/к24М30М36М45М10Б112Б114Б116Б120Б125Б130Б135Б140Б145Б150Б155Б160Б125Б230Б235Б240Б245Б255Б260Б220Ш125Ш130Ш135Ш140Ш145Ш150Ш130Ш235Ш240Ш250Ш220К125К130К135К140К120К225К230К235К240К220Б1 (09Г2С)25Б1 (09Г2С)30Б1 (09Г2С)35Б1 (09Г2С)40Б1 (09Г2С)45Б1 (09Г2С)50Б1 (09Г2С)55Б1 (09Г2С)60Б1 (09Г2С)25Б2 (09Г2С)30Б2 (09Г2С)35Б2 (09Г2С)40Б2 (09Г2С)45Б2 (09Г2С)55Б2 (09Г2С)20К1 (09Г2С)25К1 (09Г2С)30К1 (09Г2С)35К1 (09Г2С)25К2 (09Г2С)30К2 (09Г2С)35К2 (09Г2С)20Ш1 (09Г2С)25Ш1 (09Г2С)30Ш1 (09Г2С)35Ш1 (09Г2С)45Ш1 (09Г2С)30Ш2 (09Г2С)35Ш2 (09Г2С)50Ш2 (09Г2С)1,5х1250 г/к2,0х1250 г/к2,5х1250 г/к3,0х1250 г/к4,0х1500 г/к5,0х1500 г/к6,0х1500 г/к8,0х1500 г/к10,0х1500 г/к12,0х1500 г/к14,0х1500 г/к16,0х1500 г/к18,0х1500 г/к20,0х1500 г/к25,0х1500 г/к30,0х1500 г/к36,0х1500 г/к40,0х1500 г/к50,0х1500 г/к60,0х1500 г/к80,0х1500 г/к100,0х1500 г/к4,0х1500 г/к (09Г2С)5,0х1500 г/к (09Г2С)6,0х1500 г/к (09Г2С)8,0х1500 г/к (09Г2С)10,0х1500 г/к (09Г2С)12,0х1500 г/к (09Г2С)14,0х1500 г/к (09Г2С)16,0х1500 г/к (09Г2С)18,0х1500 г/к (09Г2С)20,0х1500 г/к (09Г2С)25,0х1500 г/к (09Г2С)30,0х1500 г/к (09Г2С)36,0х1500 г/к (09Г2С)50,0х1500 г/к (09Г2С)0,50х1250 х/к0,60х1250 х/к0,70х1250 х/к0,80х1250 х/к0,90х1250 х/к1,0х1250 х/к1,2х1250 х/к1,4х1250 х/к1,5х1250 х/к1,8х1250 х/к2,0х1250 х/к2,5х1250 х/к3,0х1250 х/к0,50х1250 х/к оц.0,55х1250 х/к оц.0,70х1250 х/к оц.0,80х1250 х/к оц.1,0х1250 х/к оц.1,2х1250 х/к оц.1,5х1250 х/к оц.2,0х1250 х/к оц.3,0 мм (чечевица)4,0 мм (чечевица)5,0 мм (чечевица)6,0 мм (чечевица)8,0 мм (чечевица)ПВЛ-406ПВЛ-408ПВЛ-410ПВЛ-506ПВЛ-508ПВЛ-51025х25х4,032х32х4,035х35х4,040х40х4,045х45х4,045х45х5,050х50х5,063х63х5,063х63х6,070х70х6,075х75х5,075х75х6,075х75х8,080х80х6,080х80х8,090х90х7,090х90х8,0100х100х7,0100х100х8,0100х100х10,0110х110х8,0125х125х8,0125х125х9,0125х125х10,0125х125х12,0140х140х9,0140х140х10,0160х160х10,0160х160х12,0180х180х12,0200х200х12,0200х200х16,063х40х6,075х50х5,075х50х6,0100х63х6,0100х63х8,05П6,5П8П10П12П14П16П18П20П22П24П27П30П40П5У6,5У8У10У12У14У16У18У20У22У24У27У30У40У80х60х4,0100х50х4,0100х50х5,0120х50х3,0120х60х4,0120х60х5,0160х80х4,0180х80х5,0250х125х6,015х2,515×2,820х2,825х3,232х3,240х3,040х3,550х3,050х3,515×2,820х2,825х3,232х3,240х3,550х3,557х3,057х3,576х3,076х3,589х3,089х3,589х4,0102х3,0102х3,5102х4,0108х3,5108х4,0114х4,0114х4,5127х4,5133х4,0133х4,5159х4,0159х4,5159х5,0159х6,0219х4,5219х5,0219х6,0219х8,0273х5,0273х6,0273х7,0273х8,0325х6,0325х7,0325х8,0426х6,0426х7,0426х8,0426х9,0530х7,0530х8,0530х10,057х3,576х3,589х3,5108х3,5530х7,0530х8,0530х9,0530х10,0530х12,0630х8,0630х9,0630х10,0630х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х8,0820х9,0820х10,0820х11,0820х12,0530х7,0530х8,0530х9,0530х10,0530х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х9,0820х10,01020х10,01020х12,01020х14,01220х11,01220х12,01220х14,01420х14,057х3,557х4,057х5,057х6,076х3,576х4,076х5,076х6,083х4,089х3,589х4,089х5,089х6,0102х4,0102х5,0102х6,0108х4,0108х5,0108х6,0114х5,0114х6,0121х6,0127х5,0133х4,0133х4,5133х5,0133х6,0133х8,0146х5,0146х6,0159х5,0159х6,0159х7,0159х8,0168х6,0168х7,0168х8,0219х6,0219х7,0219х8,0219х10,0273х7,0273х8,0273х10,0325х8,0325х10,0377х9,0426х9,0426х10,010х2,014х2,016х2,016х3,018х2,018х3,020х2,022х2,022х2,522х3,025х2,025х3,027х3,028х3,028х4,028х7,032х3,034х3,538х3,038х4,040х3,040х3,542х3,042х5,045х3,045х6,048х3,051х2,551х3,057х3,060х3,063х4,015х1,520х1,520х2,025х1,525х2,030х1,530х2,040х1,540х2,040х2,540х3,050х2,050х3,050х4,060х2,060х3,060х4,080х3,080х4,080х5,0100×4,0100×5,0100×6,0120х4,0120х5,0120х8,0140х5,0140х6,0160х4,0160х5,0160х6,0180х8,0100х4,0100х5,0120х4,0120х5,0140х5,0140х6,0160х5,0160х6,0160х8,020х2,025х2,030х2,040х2,040х3,050х2,050х2,550х3,050х4,060х2,060х3,080х5,080х6,0100х5,0140х5,0140х6,028х25х1,530х20х1,540х20х1,540х20х2,040х25х1,540х25х2,050х25х1,550х25х2,050х25х2,550х30х2,060х30х2,060х30х2,560х30х3,060х40х2,060х40х2,560х40х3,080х40х2,080х40х3,080х40х4,080х60х4,0100х50х3,0100х50х4,0100х60х4,0120х60х4,0120x80x4,0120х80х6,0140x60x4,0150х100х6,0160х80х5,0160х120х4,028х25х2,040х20х2,040х25х2,050х25х2,050х25х2,560х30х2,060х30х2,560х40х2,060х40х2,580х40х2,080х60х4,0120х80х4,0150х100х6,0160х120х4,0Ø 6,5 мм (в бухтах)Ø 8 мм (в бухтах)Ø 10 мм (в бухтах)Ø 12 ммØ 14 ммØ 16 ммØ 18 ммØ 20 ммØ 22 ммØ 25 ммØ 28 ммØ 30 ммØ 32 ммØ 34 ммØ 36 ммØ 40 ммØ 42 ммØ 45 ммØ 50 ммØ 52 ммØ 56 ммØ 60 ммØ 70 ммØ 80 ммØ 90 ммØ 100 ммØ 110 мм10 мм12 мм14 мм16 мм18 мм20 мм25 мм20х4,025х4,025х5,030х4,030х5,040х4,040х5,040х6,050х5,060х5,060х6,080х6,0100х8,0
Расчет
Онлайн калькулятор для расчета желебобетонных балок перекрытия дома
ДалееПересчитать
Назначение калькулятора
Соответственно СНиП 2.03.01-84 «Бетонные и железобетонные конструкции» габариты железобетонных балок перекрытия и их устройство подсчитываются по дальнейшим принципам:
- Минимальная высота балки перекрытия должна составлять не меньше 1/20 части длины перекрываемого проёма. К примеру при длине проёма в 5 м минимальная высота балок должна составлять 25 см;
- Ширина железобетонной балки устанавливается по соотношению высоты к ширине в коэффициентах 7:5;
- Армировка балки состоит минимум из 4 арматур – по два прута снизу и сверху. Применяемая арматура должна составлять не меньше 12 мм в диаметре. Нижнюю часть балки можно армировать прутами большего сечения, чем верхнюю;
- Железобетонные балки перекрытия бетонируются без перерывов заливки, одной порцией бетонной смеси, чтобы не было расслоения бетона.
Дистанцию между центрами укладываемых балок определяют длиной блоков и установленной шириной балок. К примеру, длина блока составляет 0,60 м, а ширина балки 0,15. Дистанция между центрами балок будет равна – 0,60+0,15=0,75 м.
Принцип работы
Согласно ГОСТ 26519-85 «Конструкции железобетонные заглублённых помещений с перекрытием балочного типа. Технические условия» формула расчёта полезной нагрузки железобетонных балок перекрытия складывается из следующих характеристик:
- Нормативно-эксплуатационная нагрузка на балки перекрытия с определённым коэффициентным запасом. Для жилых зданий данный показатель нагрузки составляет 151 кг на м2, а коэффициентный запас равен 1,3. Получаемая нагрузка – 151*1,3=196,3 кг/м2;
- Нагрузка от общей массы блоков, которыми закладываются промежутки между балками. Блоки из лёгких материалов, к примеру из пенобетона или газобетона, показатель плотности которых D-500, а толщина 20 см будут нести нагрузку – 500*0,2=100 кг/м2;
- Испытываемая нагрузка от массы армированного каркаса и последующей стяжки. Вес стяжки с толщиной слоя 5 см и показателем плотности 2000 кг на м3 будет образовывать следующую нагрузку – 2000*0,05=100 кг/м2 (масса армировки добавлена в плотность бетонной смеси).
Показатель полезной нагрузки железобетонной балки перекрытия составляется из суммы всех трёх перечисленных показателей – 196,3+100+100=396,3 кг/м2.
Балки под сосредоточенной нагрузкой | Онлайн калькулятор
Исходные данные:
L — длина балки, в миллиметрах;
a — координата точки приложения сосредоточенной нагрузки, в миллиметрах;
X — координата точки нахождения изгибающего момента, угла поворота и прогиба балки, в миллиметрах;
F — нагрузка, в ньютонах;
Ix — момент инерции сечения относительно оси, перпендикулярной действию нагрузки, в метрах
Е — модуль упругости материала балки, в паскалях.
Расчет балки # 1.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке консольно закрепленной балки под действием сосредоточенной нагрузки.
Граничные условия:
RL = 0 — реакция опоры в крайней левой точке;
ML = 0 — изгибающий момент в крайней левой точке;
θR = 0 — угол поворота в крайней правой точке;
YR = 0 — прогиб балки в крайней правой точке.
Расчет балки # 2.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленным концом и скользящей опорой под действием сосредоточенной нагрузки.
Граничные условия:
RL = 0 — реакция опоры в крайней левой точке;
θL = 0 — угол поворота в крайней левой точке;
θR = 0 — угол поворота в крайней правой точке;
YR = 0 — прогиб балки в крайней правой точке.
Расчет балки # 3.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленным концом и шарнирной опорой под действием сосредоточенной нагрузки.
Граничные условия:
МL = 0 — изгибающий момент в крайней левой точке;
YL = 0 — прогиб балки в крайней левой точке;
θR = 0 — угол поворота в крайней правой точке;
YR = 0 — прогиб балки в крайней правой точке.
Расчет балки # 4.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленными концами под действием сосредоточенной нагрузки.
Граничные условия:
θL = 0 — угол поворота в крайней левой точке;
YL = 0 — прогиб балки в крайней левой точке;
θR = 0 — угол поворота в крайней правой точке;
YR = 0 — прогиб балки в крайней правой точке.
Расчет балки # 5.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c шарнирными опорами под действием сосредоточенной нагрузки.
Граничные условия:
МL = 0 — изгибающий момент в крайней левой точке;
YL = 0 — прогиб балки в крайней левой точке;
МR = 0 — изгибающий момент в крайней правой точке;
YR = 0 — прогиб балки в крайней правой точке.
Расчет балки # 6.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c шарнирной и скользящей опорами под действием сосредоточенной нагрузки.
Граничные условия:
RL = 0 — реакция опоры в крайней левой точке;
θL = 0 — угол поворота балки в крайней левой точке;
МR = 0 — изгибающий момент в крайней правой точке;
YR = 0 — прогиб балки в крайней правой точке.
©ООО»Кайтек», 2020. Любое использование либо копирование материалов или подборки материалов сайта, может осуществляться лишь с разрешения автора (правообладателя) и только при наличии ссылки на сайт www.caetec.ru
Калькулятор балок. Расчет нагрузки на балки перекрытия. Нагрузка на балку: нюансы
Калькулятор балок – это опция, которая поможет произвести необходимые расчеты для получения прочной системы. Максимально же точные данные смогут предоставить профи.
Калькулятор балок: на чем он основывается
При приближении к этапу возведения перекрытия возникает необходимость грамотно рассчитать допустимую нагрузку для уже построенной конструкции. При этом необходимо учесть, что правильно высчитанная длина и толщина балок позволяет установить максимально прочную и долговечную стропильную систему.
Нужно отметить, что таким стандартным проблемам, как частичное разрушение и проседание перекрытия способствуют следующие моменты:
- Прогиб поперечин.
- Дефекты дерева.
- Чересчур большой шаг непосредственно между лагами и др.
Поэтому необходимо рассчитать нагрузку, которую будут создавать сами балки собственным весом. В целом на рассматриваемые системы давление оказывается на кручение, изгиб сечения, а также прогиб по длине.
При расчетах нужно учитывать также и климат местности, поскольку немалая нагрузка ложиться на стропила при сильном ветре, выпадении снега и т.д. Важным моментом является длина шага: малый увеличит вес конструкции, большой же станет причиной ослабевания конструкции в целом.
Рассчитываем нагрузку перекрытие из балок
Пролет – определенное расстояние между стенами. Если помещение не квадратное, то один пролет всегда короче второго. По правилам, перекрытие нужно делать по меньшему пролету. Это позволяет обустроить максимально прочную систему.
Сам брус, по стандарту должен иметь сечение 7 к 5 (высота к ширине). При таком подходе исключается деформация изделия. Прогиб же может быть максимум 2 см при длине балки 4м (то есть соотношение должно быть не больше 1 к 200).
Ниже приведены формулы, которые чаще всего используются при проведении необходимых расчетов. Прогиб можно найти, воспользовавшись такой формулой: f=L/200. Где f – нормальный прогиб, L – размер (длина) пролета, а 200 – это допустимое по нормам расстояние в см на 1 единицу проседания.
Площади поперечных сечений и масса баллок
Кроме этого, определяется момент сопротивления по формуле: W ≥ M/R. Где R представляет собой расчетное сопротивление, а М – максимальный изгибающий момент конкретной прилагаемой нагрузки. Для прямоугольных же балок можно воспользоваться формулой: W=b*h²/6/ Где h – высота, а b – ширина бруса.
Нагрузка на балку: нюансы
Особое внимание нужно уделять конструкциям, в которых перекрытие выполняет роль, как пола, так и потолка. В таких ситуациях не нужно пренебрегать лагами и точным расчетом подходящей длины шага.
Еще при корректном подходе учитывается масса утеплителя и других элементов. Стандартной полезной нагрузкой считается 150 кг/м². Для чердака этот показатель снижают до 75 кг/м².
Предложенный онлайн калькулятор позволит получить, максимально приближенные к точным, данные. В случае сомнений и вопросов обращайтесь к менеджерам компании «АртСтрой».
Понравилась статья? Расскажите друзьям!
Расчёт железобетонной балки
Не смотря на то, что заводы железобетонных изделий производят большое количество готовой продукции, все же иногда приходится делать железобетонную балку перекрытия или железобетонную перемычку самому. Практически все видели строителей-монтажников, засовывающих в опалубку какие-то железяки, и почти все знают, что это — арматура, обеспечивающая прочность конструкции, вот только определять количество и диаметр арматуры, закладываемой в железобетонные конструкции, хорошо умеют только инженеры-технологи. Железобетонные конструкции, хотя и применяются вот уже больше сотни лет, но по-прежнему остаются загадкой для большинства людей, точнее, не сами конструкции, а расчет железобетонных конструкций.
Расчёт железобетонной балки — это одна из наиболее часто встречающихся задач в частном секторе. Столкнувшись с задачей расчёта фундамента для своего дома я разложил его на множество «условно» отдельных балок, посчитал все возможные нагрузки и принялся за расчёты. Конечно, прежде всего я попытался разобраться в алгоритме расчёта и попытался посчитать всё вручную. Потом я нашёл несколько программок для расчёта жб балок и перепроверил свои расчёты. Не удовлетворившись данными этих программок, составил Exel-табличку, которая впоследствии переросла в программу калькулятор. Потом расчёты затянули меня на несколько месяцев в сопромат и программирование и как результат — вот довольно серьёзная программа расчёта ж/б балок.
С 12,01,2021 flash не поддерживается по умолчанию.
Вот способ от одного из подписчиков:
Шаг1. Удалить с компа все версии флэшплеера, у Adobe есть на сайте прога для этого.
Шаг 2. Скачать и установить флэшплеер версии 27 или ниже.
Метод работает в браузере Яндекс. Говорят, что ещё на Мозиле работает. Правда, в Хроме не работает всё равно.
После ввода любых числовых значений не забываем нажимать Enter, чтобы калькулятор их посчитал!
Процесс расчёта
Основная идея расчёта сводится к тому, чтобы добиться баланса между прочностью бетона на сжатие и прочностью арматуры на растяжение. Иногда, в процессе расчётов каких-нибудь явно нереальных балок и нагрузок, можно увидеть, что калькулятор предлагает какое-то расчётное армирование, но при этом прочность балки не обеспечивается. Это следует понимать как то, что при таком сечении балки обеспечить прочность только арматурой невозможно. Т.е. калькулятор выдаёт сечение арматуры, при котором и бетон и арматура разрушатся одновременно и при этом наращивание армирования уже не приведёт к желаемому результату. Нужно либо уменьшать нагрузки/пролёты, либо увеличивать высоту/ширину сечения бетона.
1. Геометрические параметры балки
Некоторые программки, типа «Строитель+», расчитывают балку исходя из того, что известны длина пролёта, распределённая нагрузка на балку и марка бетона. В результате расчёта мы получим высоту, ширину и количество арматуры для обеспечения прочности балки. Это на начальном этапе не так и плохо, но зачастую геометрию нам диктуют условия строительства. Например, имея газобетонную стену шириной 290мм целесообразно сделать и балку перекрытия, скажем, над гаражными воротами шириной 290мм. Или, если вы хотите утеплить в последствии эту балку 5 см пенопласта, то нужно сделать ширину балки 240мм. Высоту тоже удобнее связать с высотой блока, ну или с 0,5 высоты блока, чтобы минимизировать отходы и работу по подрезке блоков. В случае балок внутри помещения зачастую у нас могут возникнуть ограничения по высоте балки. Например, проектируя гараж мы хотели получить выход на его крышу из «французского» окна второго этажа. При этом в гараже семиметровый пролёт, перекрываемый жб балкой — условие выхода из окна накладывало на высоту балки жёстке ограничение — не более 50см. Расчитывая ленту ростверка для фундамента по технологии ТИСЭ я так-же стремился сделать его по возможности ниже, чтобы на входе в дом было минимально возможное количество ступеней.
Итак, всеми этими примерами я хотел сказать то, что геометрические параметры зачастую нам заданы внешними факторами и порой требуется посчитать, сможем ли мы вложиться в отведённое нам пространство, а если не сможем, то сколько нужно арматуры, чтобы это стало возможным. Конечно, для того, чтобы с чего-то начать подбор сечения в случае расчёта с нуля, неплохо было бы иметь какую-то отправную точку. Для этого нам нужно знать хотя бы два параметра: длину балки и нагрузку на балку. Двух этих параметров программе будет достаточно, чтобы предположить минимально возможные высоту и ширину балки (в столбике с расчётами мелким курсивом).
Пример из моей стройки. Я, не зная ещё ничего о форме своей ленты-ростверка на столбах ТИСЭ, размышлял следующим образом. Диаметр столбов ТИСЭ у меня 200мм. В процессе их заливки я местами немного ошибался, то они на пару миллиметров толще, то уже, то при бурении бур увело в сторону на 5мм, то ветер сдувал разметочную верёвочку и т.п. В общем, я принял ширину ленты 220мм (200мм — столб + 20мм запас). Далее, высота балки обычно принимается как b / 0.3 ÷ 0.5, т.е. высота лежит в диапазоне 440 ÷ 730 мм. Нагрузки от каркасного дома у меня не большие, максимум 2500кг/м.п., а максимальный пролёт между столбами равен 2800мм в свету (ограничен несущей способностью грунта и диаметром расширения столба ТИСЭ). Потому рассчитываю балку сечением 440 х 220. При таких вводных данных получается, что для армирования достаточно 2 прута диаметром 10мм в одном ряду и процент армирования лежит ниже рекомендованного порога в 0,3%. Это не плохо, но экономически необосновано — нужно слишком много бетона! Поскольку ширину балки уменьшать некуда, уменьшаем высоту. Минимально рекомендованная 250мм, округляю её до целого числа 300мм (опалубку легче делать из двух досок 150мм). Считаем. Армирования достаточно 3 х 12мм и процент армирования в оптимальных пределах. Высота в 300мм меня устраивает по эргономическим соображениям, а расход бетона снижен на 32%. Ещё парочка расчётов со значениями высоты 250мм и 350мм показала, что 250мм требует уже большего расхода арматуры, и цена за арматуру начинает перевешивать экономию на бетоне, а 350мм вроде и не плохо, но усложняется конструкция опалубки и нужно «лишних» 2 куба бетона. Конечно, я не упомянул о классе бетона! Но, у нас в городе разница за куб бетона В20 и В30 не такая уж и большая, и я выбирал всегда бетон класса В30. Известны случаи, когда реальный класс бетона несколько не соответствует заказываемому, поэтому я предпочёл заказывать бетон более высокого класса в расчёте на то, что он, вероятно, на самом деле В25, а то и вовсе В20.
2. Определение опор балки
С точки зрения сопромата, будет ли это перемычка над дверным или оконным проемом или балка перекрытия, значения не имеет. А вот то как именно балка будет опираться на стены имеет большое значение. С точки зрения строительной физики любую реальную опору можно рассматривать или как шарнирную опору, вокруг которой балка может условно свободно вращаться или как жесткую опору. Определить расчётную схему не сложно:
Балка на шарнирных опорах. Если железобетонная балка устанавливается в проектное положение после изготовления, ширина опирания балки на стены меньше 200 мм, при этом соотношение длины балки к ширине опирания больше 15/1 и в конструкции балки не предусмотрены закладные детали для жесткого соединения с другими элементами конструкции, то такая железобетонная балка однозначно должна рассматриваться как балка на шарнирных опорах. Это наиболее вероятная схема в частном домостроении.
Защемлённая на концах балка. Если железобетонная балка изготавливается непосредственно в месте установки, то такую балку можно рассматривать, как защемленную на концах только в том случае, если и балка и стены, на которые балка опирается, бетонируются одновременно или при бетонировании балки предусмотрены закладные детали для жесткого соединения с другими элементами конструкции. Во всех остальных случаях балка рассматривается, как лежащая на двух шарнирных опорах.
Консольная балка. Балка, один или два конца которой не имеют опор, а опоры находятся на некотором расстоянии от концов балки, называется консольной. Например плиту перекрытия над фундаментом, выступающую за пределы фундамента на несколько сантиметров, можно рассматривать как консольную балку.
Многопролетная балка. Иногда возникает необходимость рассчитать железобетонную балку перекрытия, которая будет перекрывать сразу две или даже три комнаты, монолитное железобетонное перекрытие по нескольким балкам перекрытия или перемычку над несколькими смежными проемами в стене. В таких случаях балка рассматривается как многопролетная на шарнирных опорах. Это уже значительно более сложная в расчёте конструкция. Её, конечно, можно рассматривать как отдельные шарнирно опёртые балки, но это совсем не так! При равных по длине пролётах самый большой изгибающий момент образуется не в пролётах, а над опорами и в этом случае особое значение приобретает рассчёт арматуры именно верхнего ряда. Мой калькулятор пока умеет рассчитывать лишь двухпролётные балки.
Лента-ростверк в фундаменте ТИСЭ однозначно относится к Многопролётным балкам, однако, я её рассчитывал, как набор несвязанных между собой шарнирно опёртых балок, нагруженных равномерной нагрузкой от стен дома. В реальности, конечно, все сегменты ленты армированы максимально длинными кусками арматуры (12 метров), соблюдая все правила армирования по расположению стыков, нахлёстов, примыканий, длин анкеровки и установке поперечных хомутов. Что даёт мне значительный запас по прочности в условиях очень «ажурного» сечения балки. Такую конструкцию целесообразнее расчитывать в два прохода: все центральные элементы — это балки с двумя защемлёнными концами, а пролёты возле углов и Т-образные примыкающие пролёты — по схеме с одним защемлённым и одним шарнирно-опираемым концами. Чем больше пролётов в балке, тем ближе она будет к подобному упрощению (начиная с 5 пролётов — разбежка ).
3. Определение нагрузки на балку
Нагрузки бывают распределёнными и сосредоточенными. В жизни, конечно, всё сложнее: распределённые нагрузки могут быть равномерно и неравномерно изменяющимися, сосредоточенные нагрузки почти всегда сопровождаются некоторыми распределёнными, а ещё все эти сочетания могут быть статическими или динамическими, или обоими одновременно! С одной стороны конструкцию следует рассчитывать на максимально неблагоприятное сочетание нагрузок, с другой стороны теория вероятности говорит о том, что вероятность такого сочетания нагрузок крайне мала и рассчитывать конструкцию на максимально неблагоприятное сочетание нагрузок, значит неэффективно тратить строительные материалы и людские ресурсы. Поэтому при расчете конструкций динамические нагрузки используются с различными поправочными коэффициентами, учитывающими вероятность сочетания нагрузок, но как показывает практика, учесть все невозможно. Для примера я покажу вам свои расчёты нагрузки на ленту-ростверк:
Как видите, динамическая нагрузка вносит очень ощутимый вклад в суммарное значение всех нагрузок, хотя она вряд ли когда-нибудь случится. Для дальнейших расчётов я округлил нагрузку в 2242кг*м.п. до 2500кг*м.п., Вдруг я на старости лет увлекусь роялем и бильярдом одновременно =)
К этой же нагрузке стоит добавить ещё и нагрузку от собственного веса балки. При размерах 0,22 х 0,3 х 3 метров объём балки составит 0,198 м³, что при плотности железобетона 2500кг на кубометр составит 495кг. В калькуляторе эти величины так-же вычисляются, и автоматически добавляются к полезной нагрузке, если стоит галочка напротив строчки «Добавлять вес балки?»
Поскольку стены дома конструктивно обшиты ОСП-плитами, равномерно распределяющими нагрузку от стоек каркаса по всему обвязочному брусу я принимаю нагрузку, как равномерно распределённую.
4. Класс арматуры
В последнее время я несколько раз уже покупал арматуру, и ни разу не видел арматуру диаметров 10 — 16мм другого класса, кроме как А500С. Это самая подходящая арматура, рекомендованная современными правилами. Тем не менее, в программу-калькулятор я включил почти всю линейку современных классов арматуры (от А240 до А1000) и те классы, которые были в старых сводах правил (типа А-I, A-II, A-III). Мало ли, кто где какую арматуру раздобудет. Для расчётов и на практике я использовал арматуру класса А500С диаметром 12мм.
5. Армирование
Этот пункт в калькуляторе находится в разделе исходных данных, однако имеет некоторую «обратную связь» от расчётов. Задавая количество прутов арматуры в растянутой зоне балки программа рассчитает требуемый диаметр этих прутов и если выбранный диаметр меньше расчётного, покажет это. Как выбрать количество прутов? Для этого в раздлах СНиП есть ряд правил, которые я описал в статье «правила армирования». В общем случае, если это не узенькая слабонагруженная перемычка над окном, рекомендуется не менее двух прутов. Есть ограничения и на максимальное количество прутов, обусловленное расстоянием между прутами. Это минимальное расстояние определено необходимостью свободного протекания бетонной смеси в тело ленты между стержнями арматуры фундамента при заливке бетона, возможностью его уплотнения и хорошей связи бетона с арматурой для совместной работы под нагрузкой. Минимальное расстояние между стержнями продольной арматуры не может быть меньше наибольшего диаметра стержней арматуры и не менее 25 мм для нижнего ряда арматуры и 30 мм — для арматуры верхнего ряда при двух рядах армирования. Таким образом, максимальное количество прутов:
N=b-2a/(D+25)
округлённое до меньшего целого. В моём примере ширина балки b=220мм, толщина защитного слоя a=35мм (задана пластиковыми фиксаторами арматуры типа «звёздочка»), диаметр арматуры D=12мм:
N=220-2*35/(12+25)=4
С целью уменьшения арматурных работ я выбрал 3 прута. До расчётов диаметра мы еще дойдём.
6. Максимально допустимый относительный прогиб
Все строительные, и не строительные тоже, конструкции прогибаются! Не бывает таких материалов, которые не гнутся совсем. Железобетон не исключение, он может прогибаться под нагрузками в некоторых пределах без разрушительных последствий, причём порой на достаточно большие величины. СНиП 2.01.07-85 «Нагрузки и воздействия» регламентирует максимально допустимые прогибы, причем часть из этих ограничений связаны не с конструктивными проблемами бетонных балок, а просто с эстетическими (некрасиво, если плита перекрытия над головой прогибается на 10см, не смотря на то, что прочность обеспечена!) Выбираем требуемый в конкретном случае прогиб. В моём примере выбран прогиб 1/200, что означает, что при пролёте 3 м максимальный прогиб может составить 15 мм.
7. Изгибающий момент (начало расчётов)
Определение изгибающего момента — ключевое действие в расчёте. Все последующие вычисления будут опираться на эту величину. К сожалению, существует очень много самых разнообразных случаев приложения нагрузки к балке, да и балки бывают на разных опорах, да ещё и балки бывают статически определимые и неопределимые. Потому нету одной универсальной формулы, по которой можно вычислить изгибающий момент в любой ситуации (возможно, математики скажут, что я не прав, но двойные интегралы в уравнениях общего вида лежат за гранью моего понимания). Для определения наиболее подходящей для каждого конкретного случая формулы я порекомендую вот этот сайт, формулами которого я пользовался для написания своего калькулятора. В моём примере с равномерно распределённой нагрузкой (2500кг/м + собственный вес балки 495 кг / 3 м = 2665 кг/м) и шарнирно опёртой балкой изгибающий момент считается по формуле:
М=ql²/8
М=2665 х 3²/8=2998 кгс*м
Если бы нагрузка была сосредоточенной посередине балки, то: М=Ql/4.
8. Высота сжатой зоны
Следующим важным шагом является определение высоты сжатой зоны бетона и сравнение её с граничным условием.
Железобетон — это композитный материал, прочностные свойства которого зависят от множества факторов, точно учесть которые при расчете достаточно сложно. Кроме того бетон хорошо работает на сжатие, а арматура хорошо работает на растяжение, а при сжатии возможно вспучивание арматуры. Поэтому конструирование железобетонной конструкции сводится к определению сжатых и растянутых зон. В растянутых зонах устанавливается арматура. При этом высота сжатой и растянутой зоны зараннее неизвестна и потому применять обычные методы подбора сечения, как для деревянной или металлической балки, не получится.
Для начала определяем граничную высоту сжатой зоны. Это такая высота бетона, при которой его предельное напряжение на сжатие наступает одновременно с предельным напряжением в арматуре на растяжение. Т.е. при такой высоте сжатой зоны будет достигнут баланс между двумя разнонаправленными силами, сжатием и растяжением, и при превышении нагрузки произойдет одновременное разрушение бетона и обрыв арматуры. Граничная высота считается по следующей формуле:
ξr= ω/(1+Rs/Rpr*(1- ω/1,1))
где ω — характеристика сжатой зоны бетона, определяемая по формуле:
ω = k — 0,008 · Rb
где в свою очередь k — коэффициент, принимаемый равным для бетона: тяжёлого — 0,85; мелкозернистого — 0,80;
Rb — сопротивление бетона класса В25 сжатию: 14.5 МПа.
Итого: ω = 0,85 — 0,008 · 14,5 = 0,734.
Rpr — предельное напряжение в арматуре сжатой зоны сечения, принимаемое равным 500 Н / мм²
Rs — сопротивление арматуры класса А500 растяжению, 435 МПа.
ξr=0,734/(1+435/500*(1-0,734/1,1))=0,57
Поскольку это относительная высота, её можно перевести в абсолютную: ξr*h=171мм.
Высота сжатой зоны бетона c учётом сжатых стержней арматуры:
x=(RsAs-RscAsc)/(Rb*b)
где As — площадь сечений растянутой арматуры, в нашем примере 3 прута по 12мм, Asc — площадь сжатой арматуры (2 прута 10мм):
As=пR²*N;
As=3,14*0,6²*3=3,39 см² Asc=3,14*0,5²*2=1,57 см²
x=(435*3,39-400*1,57)/(14,5*22)=2,66 см
9. Коэффициенты Аm и Ar
Расчёт требуемой площади арматуры можно вести по алгоритму, изображённому ниже:
Для расчёта необходимого сечения арматуры нужно вычислить коэффициент Аm.
Аm=М/(Rb*h0²*b)
Поскольку М у нас в кг*м, Rb в Мпа, а величины b и h0 в см нужно всё привести к единым размерностям. М=2998 кг*м=299800 кг*см, Rb=14.5 МПа=147,86 кг/см² , теперь можно считать:
Am=299800/(147,86*26,5²*22)=0,131
Если значение Am будет больше Ar, то потребуется увеличить сечение бетонной балки, или повысить класс бетона. Если же таких возможностей или желаний нет, то необходимо устанавливать арматуру в сжатой зоне бетона!
Коэффициент Ar вычисляется по формуле:
Ar=ξr(1-0,5ξr)
Ar=0,57(1-0,5*0,57)=0,408
Условие Am<Ar у нас выполняется, значит сжатой арматуры добавлять не требуется.
10. Площадь растянутой арматуры
Расчёт необходимой площади сечения растянутой арматуры ведётся по формуле:
Fa=M/(Rs*h0*η)
где η = 0,5*(1+√(1-2*Am)) = 0,5*(1+√0,738) = 0,93
Поскольку у нас в расчёте опять размерности не совпадают, приведём все данные к единой системе, для удобства — к сантиметрам.
Rb=14.5 МПа=147,86 кг/см², Rs=435 МПа=4435,76 кг/см² .
Fa=299800/(4435,76*26,5*0,93)=2,74 см²
Поскольку количество стержней мы уже предварительно выбрали (N=3), то площадь сечения одного стержня должна быть не менее Fa/N = 2,74 / 3 = 0,914 см². Несложно посчитать диаметр этого стержня:
D=√(S/π)*20 D=10,79 мм
Округляем до ближайшего большего значения из номенклатурного ряда — 12мм. Итого, получается для армирования балки из моего примера достаточно 3 прута арматуры диаметром 12мм.
11. Проверка
Поскольку площадь растянутой арматуры отличается от расчётной, можно провести обратный расчёт для того, чтобы узнать, насколько большой у нас получился запас прочности. Сначала вновь пересчитываем площадь арматуры:
As=N*π*(D/2)² = 3,39 см²
Затем считаем максимальный изгибающий момент. Если условие Am<Ar выполняется и высота сжатой зоны х>0, то используется формула:
Mmax=Rb*b*х*(h0-0.5*х)+Rsс*Asс*(h0-a)
Mmax=147,86*22*2,66*(26,5-0,5*2,66)+4078,86*1,57*(26,5-3,5) =365078 кг*см (3650,7 кг*м = 35,8 кН*м)
где a — толщина защитного слоя бетона 3,5 см, Rsc — Предел прочности арматуры на сжатие Rsc=400 МПа=4078,86 кг/см²
Если х меньше или равен нулю, то используется другая формула: Mmax=Rs*As*(h0-а)
А если не выполняется условие Am<Ar, то: Mmax=Ar*Rb*b*h0²+Rsс*Asс*(h0-a)
Для того, чтобы перевести это значение в распределённую нагрузку, воспользуемся формулой из пункта 7:
q=8M/l²
q=8*3650,7/3²=3245 кг*м
Поскольку наша расчётная нагрузка составляет 2665 кг*м (с учётом собственного веса), то получается запас по прочности 21%.
12. Процент армирования
Процент армирования балки, это не самая критически важная величина в расчёте, потому я её оставил на последнем месте. Считается эта величина по формуле:
μ = (Fa+Fa’)/b*h0*100
μ=(3,39+1,57)/(22*26,5)*100=0,85%
Существуют рекомендованные диапазоны процента армирования балок от 0,3 до 4% (для колонн до 5%), выведенные изходя из экономических и конструктивных соображений, и наш результат отлично вписывается в этот диапазон.
13. Прогиб
Нередко бывает так, что прочность балки по первой группе предельных состояний достаточна, а вот расчёт по второй группе выходит за пределы допустимых деформаций. Потому расчёт на прогиб мне показался достаточно необходимым, чтобы потратить своё время и включить его в калькулятор. Приводимый ниже расчет не совсем соответствует рекомендациям СНиП 2.03.01-84 и СП 52-101-2003, тем не менее позволяет приблизительно определить значение прогиба по упрощенной методике. И хотя шарнирно опертая безконсольная однопролетная балка c прямоугольной формой поперечного сечения, на которую действует равномерно распределенная нагрузка — это частный случай на фоне множества возможных видов нагрузок, расчетных схем и геометрических форм сечения, тем не менее это очень распространенный частный случай в малоэтажном строительстве.
Прогиб балки для моего примера считается по формуле:
f = k5qlᶣ/384EIp
Эта формула очень похожа на класическую формулу прогибов, как в расчётах деревянных элементов и отличается наличием коэффициента k. Этот коэффициент учитывает изменение высоты сжатой области сечения по длине балки при действии изгибающего момента. При равномерно распределенной нагрузке и работе бетона в области упругих деформаций значение коэффициента для приближенных расчетов можно принимать k = 0.86. Использование этого коэффициента позволяет определять прогиб балки (плиты) переменного сечения, как для балки постоянного сечения с высотой hmin. Таким образом в приведенной формуле остается только 2 неизвестных величины — расчетное значение модуля упругости бетона и момент инерции приведенного сечения Ip в том месте, где высота сечения минимальна. Остается только определить этот самый момент инерции, а модуль упругости примем равный начальному. Момент инерции приведённого сечения Ip вычисляется довольно сложным и запутанным методом, в процессе которого необходимо решать кубическое уравнение, поэтому, если очень хочется вникнуть в суть и пересчитать всё самому, отправлю вас на сайт, где этот метод описан по шагам с картинками, чтобы совсем уж не копировать сайт автора )
Момент инерции балки J и момент сопротивления W калькулятор расчитывает по методике, описанной на указанном сайте и выдаёт результат в двух первых строчках правого столбца с расчётами.
14. Прочность по наклонным сечениям
Этим расчётом никогда нельзя пренебрегать, поскольку бетон не переносит
растягивающих усилий, а возле опор, на которые опирается балка, создаются
именно такие усилия, которые к тому-же не скомпенсированы никакой арматурой
(если не ставить хомуты). Если расчёт по прогибу и по прочности проходит, то это
совсем не означает, что балка не разрушится возле опоры из-за наклонной трещины.
Суть возникновения этой трещины изображена на картинке справа.
Для начала нам нужно определить реакции опор.
Поскольку мы рассматриваем нашу балку как шарнирно опёртую, то реакции левой и правой опор будут равны между собой, т.е. нагрузка между ними распределиться поровну.
Qопоры = q*L*0,5 = 2665 * 3 * 0,5 = 3998 кг = 39,2 кН (4т на каждую опору)
Прочность балки по наклонным сечениям обеспечивается прочностью бетона и поперечной арматуры, расположенной в теле балки.
Выясняем необходимость постановки поперечного армирования по расчету из условия:
Qопоры ≤ Qmin
где Qmin — расчетная поперечная сила, воспринимаемая железобетонным элементом без поперечной арматуры.
Расчетную поперечную силу Qmin, воспринимаемую элементом без вертикальной и (или) наклонной арматуры, допускается определять по формуле (7.78a) п.п. 7.2.1.6 СНБ 5.03.01-02 :
Qmin = ϕс * Rbt * b * ho
где коэффициент ϕс принимается равным:
для тяжелого бетона — 0,6;
для мелкозернистого — 0,5.
Rbt — сопротивление бетона растяжению Rbt=1,05 МПа=1050 кПа, а b и h0 выражены в миллиметрах.
Qmin = 0,6 * 1,05 * 220 * 265 = 36729 H = 36,7 кН
Поскольку Qопоры (39,2 кН) > Qmin (36,7 кН), бетон возле опоры не выдерживает нагрузки и требуется расчёт поперечного армирования.
15. Поперечное армирование
Диаметр хомутов в вязанных каркасах должен быть не менее 5 мм при h ≤ 800 мм и 8 мм при h > 800 мм. Высота нашего сечения 300 мм, но для хомутов у нас запасена арматура диаметром 6мм. Хомуты представляют из себя изогнутую рамочку, обхватывающую продольную арматуру, а значит площадь сечения хомута является удвоенной площадью сечения арматуры диаметром 6мм:
Asw = 3,14*0,3²*2 = 0,5652 см².
Максимально допустимый расчётный шаг хомутов определяем по формуле (Пособие по проектированию жбк, к СНиП 2.03.01-84 п.п. 3.29 (46)):
Smax = ϕb4 * Rbt * b * ho²/Q
Smax = 1,5 * 1050 кПа * 0,22 м * 0,265² м / 39,2 кН = 0,62 м
где фb4 | фb3 | фb2:
— для тяжёлого бетона: 1,5 | 0,6 | 2,00
— для мелкозернистого и лёгкого плотностью выше D 1900: 1,2 | 0,5 | 1,7
— для лёгкого D < 1900 и пористого: 1,0 | 0,4 | 1,5
Однако, согласно СНБ 5.03.01-02 п.п. 11.2.21, в железобетонных элементах, в которых поперечная сила не может быть воспринята только бетоном, поперечную арматуру следует устанавливать с выполнением следующих конструктивных требований, определяющих шаг поперечных стержней:
— при h ≤ 450 мм — не более h/2 и 150 мм;
— при h > 450 мм — не более h/3 и 300 мм;
— не более 3/4h и 500 мм;
Таким образом, в средней части пролета шаг поперечных стержней принимаем S = 3/4*30 = 22 см, (что не превышает 3/4h = 3/4*30 = 22,5 см). Исходя из равномерного распределения по длине центральной части у меня получилось 25 см, что, в принципе, допустимо в виду незначительного превышения Qопоры над Qmin.
В приопорных участках шаг поперечных стержней не должен превышать 15 см и не более h/2 = 30/2 = 15 см. Принимаем 15 см.
Вычисляем интенсивность усилий в поперечных стержнях на единицу длины балки:
qs = Rsw * Asw / S
qs = 290 000 кПа * 0,00005652 м² / 0,15 м = 109,27 кН/м
где Rsw — сопротивление растянутой поперечной арматуры класса АIII = 290 МПа;
Asw — площадь сечения арматуры хомута;
S — расстояние между хомутами в этой проекции, S = 15 cм.
Минимальная интенсивность:
qsmin = фb3 * Rbt * b / 2
qsmin = 0,6 * 1050 * 0,22 /2 = 69,3 кН/м
Требуемая интенсивность:
qsтр = Q² / (4 * Mb)
где Mb = фb2 * Rbt * b * ho²
Mb = 2 * 1050 * 0,22 * 0,265² = 32,44 кН·м
qsтр = 39,2² / (4 * 32,44) = 11,84 кН/м
Так как принятая интенсивность (109 кН/м) больше требуемой (11,84 кН/м) и больше минимальной (69,3 кН/м), оставляем шаг S = 15 см.
16. Ширина приопорных участков
Ширину приопорных участков вычислим по длине проекции опасной наклонной трещины на продольную ось балки:
с0 = √(Mb/qs) = √(32,44 / 109,27) = 0,55 м
Учитывая границы с0 в расчёте (ho < c0 < 2ho), принимаем с0 = 53 см. Несущую способность наклонного сечения проверяем по условию:
Qmax = Mb / c0 + qs * c0 = 32,44 / 0,55 + 109,27 * 0,55 = 119 кН
Qmax (119 кН) > Qопоры (39,2 кН)
Условие выполняется! Такой запас несущей способности у нас образовался благодаря хомутам диаметром 6 мм. Для данного случая можно было использовать хомуты диаметром 5мм, которые даже в приопорных учасках можно было бы ставить на расстоянии, как и в средней части пролёта — 25 см, но требования СНБ написаны не просто так!
P.S.: Если у вас балка планируется неразрезная многопролётная и с более-менее равными пролётами (+/-10%), и вы её надеетесь посчитать самостоятельно, то вам может пригодиться график эпюр изгибающих моментов. Для совсем ручного счёта рекомендую пролистать статейку про монолитное реблисто-балочное перекрытие.
Калькулятор подбора деревянных двутавровых балок
SIA I-beams производит износоустойчивые деревянные двутавры. Такие балки показали себя как незаменимый стройматериал при строительстве зданий в Северной Америке, понемногу они начинают завоевывать и рынки Европы.
Чтобы правильно произвести расчет необходимого количества балок, мы создали расчетный калькулятор, который вам поможет быстро и удобно рассчитать шаг между балками и их тип в зависимости от расстояния между стенами и от нагрузок в конкретном случае.
Как пользоваться калькулятором:
- Вводим расчетную длину пролета. Для балок перекрытия — это наибольший пролет, т.е. наибольшее расстояние между соседними стенами, на которые опирается балка. Для стропил кровли – это горизонтальное расстояние (проекция мест опоры, обычно расстояние между осями) между местами опора балки (сама балка длиннее, чем эта проекция, т.е. чем больше угол, тем длиннее балка).
- Для стропил кровли вводим угол наклона. Угол наклона – наклон стропил к горизонтали.
- Вводим шаг – это межцентровое расстояние между соседними балками.
- 4. Можно изменить постоянную нагрузку. В соответствии с нормативом EN 1991, постоянную нагрузку рассчитывают по плотности конструкции пола/перекрытия/крыши, помноженной на коэффициент надежности. Согласно EN 1990, коэффициент надежности для постоянных нагрузок — 1,35, а для временных — 1,5.
- Можно изменить временную нагрузку. В соответствии с нормативом EN 1991, величины временной нагрузки принимаются в зависимости от предполагаемого использования перекрытия. Для перекрытий жилых помещений можно принимать временную нагрузку 200 kg/m2. При расчете стропильной системы нагрузки от снега принимаются согласно LBN-003-1, таблица 16.2. Для Риги это равняется 125 kg/m2.
*В расчетном калькуляторе включено определение расчетной нагрузки при соответствующих коэффициентах надежности: согласно EN 1990 для постоянных нагрузок это — 1,35 а для временных нагрузок — 1,5. В калькулятор вводятся нагрузки без учета коэффициентов надежности. – это повторение из п.4.
*Величина используемой расчетной нагрузки будет индивидуальной — в зависимости от конкретной ситуации.
- Когда все упомянутые данные введены в таблицу, можно ознакомиться с результатом. Внизу находится табличка с имеющимися в нашем ассортименте балками. Зеленым цветом закрашены все балки, которые можно использовать, а красным – несущая способность которых не соответствует заданным вами параметрам. Чтобы изменить результат, советуем изменить шаг балок.
Бесплатный калькулятор луча | Калькулятор изгибающего момента, поперечной силы и прогиба
Добро пожаловать в наш бесплатный онлайн-калькулятор диаграмм изгибающего момента и поперечной силы, который может генерировать диаграммы реакций, поперечных сил (SFD) и изгибающих моментов (BMD) консольной балки или просто поддерживаемой балки. Используйте этот калькулятор пролета балки, чтобы определить реакции на опоры, построить диаграмму сдвига и момента для балки и рассчитать прогиб стальной или деревянной балки. Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки.Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает в себя полное программное обеспечение для структурного анализа.
Используйте интерактивное окно выше, чтобы просмотреть и удалить длину балки, опоры и добавленные нагрузки. Любые внесенные изменения автоматически перерисовывают диаграмму свободного тела для любой балки с опорой или консольной балкой. Калькулятор реакции балки и расчет изгибающего момента будут запущены после нажатия кнопки «Решить» и автоматически сгенерируют диаграммы сдвига и изгибающего момента.Вы также можете щелкнуть отдельные элементы этого калькулятора балки LVL, чтобы редактировать модель.
Калькулятор пролета балки легко рассчитает реакции на опорах. Он может рассчитывать реакции на опорах консольных или простых балок. Это включает в себя расчет реакций консольной балки, которая имеет изгибающий момент, а также силы реакции x, y.
Вышеупомянутый калькулятор пролета стальной балки — это универсальный инструмент для проектирования конструкций, используемый для расчета изгибающего момента в алюминиевой, деревянной или стальной балке.Его также можно использовать в качестве калькулятора несущей способности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Он способен выдерживать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузки и 2 момента. Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками (UDL), треугольными распределенными нагрузками или трапециевидными распределенными нагрузками. Все нагрузки и моменты могут быть направленными как вверх, так и вниз по величине, что должно учитывать наиболее распространенные ситуации анализа балок.Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Одна из самых мощных функций — использование его в качестве калькулятора отклонения балки (или калькулятора смещения балки). Это можно использовать для наблюдения расчетного прогиба балки с опорой или консольной балки. Возможность добавлять формы сечения и материалы делает его полезным в качестве калькулятора деревянных балок или в качестве калькулятора стальных балок для проектирования балок lvl или i.На данный момент эта функция доступна в SkyCiv Beam, который имеет гораздо больше функций для проектирования деревянных, бетонных и стальных балок.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений. Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и совершенствовать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Размеры стальной балки| SkyCiv
Наличие хорошего ресурса для размеров двутавровых балок очень важно при проектировании конструкций.Для нас, как инженера-строителя, важно определить секции, которые не только безопасны, но и рентабельны. С помощью приведенной ниже таблицы размеров стальных балок SkyCiv стремится получить бесплатный ресурс, к которому можно будет получить доступ в любое время через браузер. Приведенная ниже таблица размеров стальных балок поможет инженерам-строителям найти подходящий размер и форму, которые вам нужны для вашего проекта. Эти свойства важны при проверке прочности секции, что является само определение конструкции конструкции.
Таблица размеров стальных балок — это интерактивная таблица, в которой перечислены размерные и геометрические свойства сечения. Эти свойства могут помочь инженерам найти желаемый стальной профиль, который они ищут. Просто выберите систему единиц измерения, библиотеку, прежде чем выбирать форму, чтобы отобразить размеры балки этой формы. Библиотека содержит разделы из Австралии, США, Канады, Великобритании и Европы. Программное обеспечение извлекает размеры балки непосредственно из базы данных Structural 3D, которая является основным программным обеспечением для трехмерного структурного анализа платформы SkyCiv, которое также доступно для использования в веб-браузере.Эта информация обычно требует, чтобы пользователь держал под рукой ручные схемы или схемы стальных балок, что может доставлять неудобства, т. Е. Если у пользователя есть копия. Хотя приобретение руководства по стали требует денежных затрат, мы должны еще раз подчеркнуть, что справочная таблица SkyCiv легко доступна здесь бесплатно.
Некоторые из размеров, которые может отображать этот инструмент:
- Размеры двутавровой балки
- Размеры S-образной балки
- Квадрат полый / HSS Размеры
- Круглые размеры из быстрорежущей стали
- Размеры балки с широким фланцем
- Т-образная балка Размеры
- Размеры каналов
- Размеры уголков
- Имперские и метрические размеры балки
Приведенные выше размеры стальных секций должны дать пользователю возможность легко получить доступ к свойствам элементов и размерам часто используемых секций в различных библиотеках по всему миру.Мы надеемся, что инженеры найдут ссылки на эти размеры и размеры стальных балок, которые будут полезны для их рабочего процесса. Опять же, в настоящее время существуют размеры и размеры стали для профилей из Австралии, США, Великобритании, Европы и Канады. Если конкретная используемая вами библиотека недоступна, вы можете связаться с нами здесь. Мы открыты для улучшения и расширения нашей базы данных. Еще одним замечательным аспектом этого инструмента является то, что он может преобразовывать размеры балки из метрических в британские и наоборот. Это экономит время инженера при работе с единичными системами и снижает риск ошибки в расчетах.
Свойства сечения, отображаемые в приведенной выше таблице, включая площадь поперечного сечения (A), полярный момент инерции (J), момент площади (Iz, Iy), модуль сечения и постоянную деформации (Iw). Эти результаты чрезвычайно важны при выборе конструкционной стали для конструкций балок и колонн. Это свойства, которые контролируют количество и тип силы, которую может принять стальной элемент.
Здесь, в SkyCiv, у нас есть ряд программного обеспечения (бесплатного и платного), которое позволяет инженерам моделировать и проектировать свои конструкции.Наш калькулятор свободных балок — это простой в использовании калькулятор, который помогает анализировать консольные балки и балки с простой опорой. Вы также можете воспользоваться нашим калькулятором ферм для быстрого анализа 2D ферм. Для небольших 2D-рам вы можете воспользоваться нашим бесплатным калькулятором несущих рам. Для типичных форм из стали нестандартных размеров калькулятор свободного момента инерции является хорошим средством для определения их геометрических характеристик и характеристик сечения.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений.Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и совершенствовать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Калькулятор нагрузки на балку
Этот калькулятор нагрузки на балку поможет вам определить реакции на опоры балки с простой опорой из-за вертикальных точечных нагрузок или сил. С помощью этого калькулятора вы узнаете, что такое реакция опоры , и научитесь основам расчета грузоподъемности балки.
Знание того, как найти опорные реакции, — отличное место для начала при анализе балок, например, при определении отклонения балки. Продолжайте читать, чтобы узнать больше.
Что такое реакция поддержки?
Согласно третьему закону движения Ньютона , каждая сила, действующая на объект, имеет равную и противоположную реакцию. Если вы пытаетесь оттолкнуться от чего-то, скажем, стены, вам кажется, что стена также отталкивается от вас. Именно это и описывает третий закон движения Ньютона.
В инженерном деле элементы конструкции, такие как балки и колонны, взаимодействуют друг с другом в точках пересечения. Представьте себе балку, которая поддерживается на месте двумя колоннами. Вес балки давит на колонны, и, благодаря третьему закону движения Ньютона, мы можем также сказать, что колонны оказывают на балку эквивалентную противоположную силу реакции. Мы называем эти силы реакции опорными реакциями .
На балке с простой опорой реакции опоры на каждом конце балки могут быть одинаковыми или иметь разные значения.Их значения зависят от приложенных нагрузок на балку. Если на более близком расстоянии к одной опоре находится больше нагрузок, эта опора испытывает большую силу и, следовательно, испытывает большую реакцию.
Как рассчитать опорные реакции в балке?
Поскольку опорные реакции действуют в направлении, противоположном силе, мы можем сказать, что вся система находится в равновесии. Это означает, что балка не движется, а сумма сил и моментов дает ноль. Приравнивая моменты от нагрузки к моментам от опорных реакций , мы можем затем определить реакции на опорах.
Так же, как при расчете крутящего момента, мы также можем выполнить суммирование моментов на каждой опоре, чтобы найти реакции. Ниже мы выражаем сумму, Σ , моментов на опоре A, чтобы найти реакцию на опоре B, обозначенную как R B , как показано ниже:
Σ (F * x) - (R B * пролет) = 0
(F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) +... + (F n * x n ) - (R B * диапазон) = 0
где:
-
F,F 1,F 2,F 3иF n— Точечные нагрузки на балку на расстоянияхx,x 1,x 2x 3иx nиз опоры A соответственно; -
R B— Реакция на опоре B; и -
пролет— Длина балки между опорой A и опорой B.
Переставив уравнение, мы можем выделить R B следующим образом:
R B * диапазон = (F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) + ... + ( F n * x n )
R B = ((F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) +... + (F n * x n )) / пролет ✔
Теперь, когда у нас есть выражение для нахождения R B , и поскольку мы знаем, что общие приложенные силы равны сумме реакций, теперь мы можем также найти реакцию на опоре A R A , используя следующие уравнения:
Σ (F) = Rᴀ + Rʙ
R A = Σ (F) - Rʙ ✔
Пример расчета реакции опоры
Предположим, у нас есть 4.0-метровая балка с простой опорой длиной с приложенной точечной нагрузкой 10,0 килоньютон (кН) на расстоянии 2,0 метра от опоры A и другой точечной нагрузкой 3,5 кН в 1,5 метрах от опоры B , как показано ниже:
Для расчета для R B сформулируем уравнение моментного равновесия следующим образом:
R B = (F 1 * x 1 + F 2 * x 2 ) / промежуток
R B = (10 кН * 2.0 м + 3,5 кН * (4,0 м - 1,5 м)) / 4,0 м
R B = (20 кН-м + 3,5 кН * 2,5 м) / 4,0 м
R B = (20 кН-м + 8,75 кН-м) / 4,0 м
R B = 7,1875 кН
Суммируя силы, получаем:
Σ (F n ) = 0
Факс 1 + Факс 2 + (-Rᴀ) + (-Rʙ) = 0
10 кН + 3.5 кН + (-Rᴀ) + (-7,1875 кН) = 0
R A = 10 кН + 3,5 кН - 7,1875 кН
R A = 6,3125 кН
Обратите внимание, что для этого суммирования , мы рассмотрели все нисходящие силы как положительные и все восходящие силы как отрицательные . Основываясь на наших расчетах выше, мы теперь получили реакции на опорах A и B, которые составляют 6,3125 кН и 7,1875 кН , соответственно.
Также обратите внимание, что в этом примере и в калькуляторе нагрузки на балку мы предполагали, что балка невесомая. Однако, если указан вес балки, вы можете рассматривать ее как еще одну направленную вниз точечную нагрузку в центре или центроиде балки.
Использование нашего калькулятора нагрузки на балку
Наш калькулятор легок и прост в использовании. Все, что вам нужно сделать, это ввести пролет балки , величину точечных нагрузок и их расстояние от опоры A .Сначала вы увидите поля только для двух нагрузок (Загрузка 1 и Загрузка 2), но как только вы введете значение для x 2 , появятся поля для нагрузки 3 и так далее.
Если вы хотите ввести восходящую нагрузку, просто введите отрицательное значение для величины нагрузки. Всего в наш калькулятор нагрузки на балку можно ввести до 11 точечных нагрузок.
Хотите узнать больше?
Теперь, когда вы узнали, как рассчитать допустимую нагрузку на балку, определив реакции на опорах, возможно, вы также захотите узнать больше о том, что такое прогиб балки и изгиб балки.
Калькулятор деревянных балок | Какой размер мне нужен?
Рассчитайте необходимый размер балки, балки или перекрытия из сосны № 2 или LVL. Охватывает любой пролет и любую нагрузку с высокой точностью. Дважды проверьте себя с этими графиками диапазона. Работает только с равномерно распределенными нагрузками.
Есть два разных типа нагрузок. Это либо внешняя, либо внутренняя нагрузка. Другими словами, он будет либо на внешней стене, либо где-то внутри.Нагрузка на внешнюю стену с чистыми пролетными фермами составляет ровно половину нагрузки на каждую стену. Например, если здание имеет размеры 24 x 24 и имеет фермы, а нагрузка на крышу будет составлять 30 фунтов снеговой нагрузки, а потолок без хранилища будет таким. Это будет вдвое больше нагрузки на внешние стены по сравнению со зданием с центральной стеной. Калькулятор учитывает все это. Вам нужно только выбрать все применяемые нагрузки.
Большинство внутренних балок должны учитывать нагрузку на крышу.Если есть какие-либо вопросы по другому поводу, вам следует обратиться к поставщику или инженеру. Этот калькулятор соответствует 90% приложений в Международной книге кодов жилищного строительства 2012 года.
Здравый смысл
По моему опыту никогда не использовать балку меньше двухслойной 2 x 8. Независимо от того, что сказано в технических характеристиках. Эти небольшие области обычно представляют собой дверные проемы внутри, и людей учат, что эти области являются самым надежным местом в доме в случае возникновения чрезвычайной ситуации.
Подшипник
В соответствии с нормами IRC 2012 года любая балка, балка или коллектор никогда не должны иметь пеленг менее 1 1/2 дюйма. Что-нибудь 5 ‘и выше мы всегда как минимум вдвое калечим. На более длинных пролетах балке может потребоваться гораздо больше места для опоры, как указано в этой таблице.
Крепление
Балки, состоящие из более чем одного слоя, должны скрепляться вместе гвоздями или болтами. Код IRC 2012 года требует минимум 32 ″ O.C. в шахматном порядке с использованием гвоздя размером не менее 3 ″ на 120 ″.На собственном опыте мы научились использовать гвоздь с пазом размером не менее 3 1/4 дюйма x 131 дюйм в столбике из четырех на каждую ногу вниз по ламинату.
Единственный раз, когда вам когда-либо понадобится использовать болты, будет, если материал будет иметь такие серьезные деформации, как плохая «чашка», которую невозможно преодолеть гвоздями.
Балки — поддерживаются с обеих сторон
Напряжение в изгибающейся балке может быть выражено как
σ = y M / I (1)
, где
σ = напряжение (Па (Н / м ) 2 ), Н / мм 2 , psi)
y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = изгибающий момент (Нм, фунт дюйм)
I = момент инерции (м 4 , мм 4 , в 4 )
Калькулятор ниже можно использовать для расчета максимального напряжения и прогиба балок с одной одиночной или равномерно распределенной нагрузкой.
Балка, поддерживаемая на обоих концах — равномерная непрерывная распределенная нагрузка
Момент в балке с равномерной нагрузкой, поддерживаемой на обоих концах в положении x, может быть выражен как
M x = qx (L — x) / 2 (2)
где
M x = момент в положении x (Нм, фунт дюйм)
x = расстояние от конца (м, мм, дюйм)
Максимум момент находится в центре балки на расстоянии L / 2 и может быть выражен как
M max = q L 2 /8 (2a)
где
M макс = максимальный момент ( Нм, фунт-дюйм)
q = равномерная нагрузка на единицу длины балки (Н / м, Н / мм, фунт / дюйм)
9039 1 L = длина балки (м, мм, дюйм)
Максимальное напряжение
Уравнения 1 и 2a могут быть объединены для выражения максимального напряжения в балке с равномерной поддерживаемой нагрузкой на обоих концах на расстоянии L / 2 как
σ max = y max q L 2 / (8 I) (2b)
где
σ max = максимальное напряжение (Па (Н / м 2 ), Н / мм 2 , psi)
y max = расстояние до крайней точки от нейтральной оси (м, мм, дюйм)
- 1 Н / м 2 = 1×10 -6 Н / мм 2 = 1 Па = 1.4504×10 -4 фунт / кв. Дюйм
- 1 фунт / дюйм (фунт / дюйм 2 ) = 144 фунт / кв. Дюйм (фунт на / фут 2 ) = 6 894,8 Па (Н / м 2 ) = 6,895×10 — 3 Н / мм 2
Максимальный прогиб :
δ max = 5 q L 4 / (384 EI) (2c)
где
δ макс = максимальный прогиб (м, мм, дюйм)
E = Модуль упругости (Па (Н / м 2 ), Н / мм 2 , psi)
Прогиб в положении x:
δ x = qx ( L 3 — 2 L x 2 + x 3 ) / (24 EI) (2d)
Примечание! — прогиб часто является ограничивающим фактором при проектировании балки.Для некоторых применений балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимого прогиба.
Силы, действующие на концы:
R 1 = R 2
= q L / 2 (2e)
где
R = сила реакции (Н, фунт)
Пример — балка с равномерной нагрузкой, метрические единицы
Балка UB 305 x 127 x 42 длиной 5000 мм несет равномерную нагрузку 6 Н / мм .Момент инерции балки составляет 8196 см 4 (81960000 мм 4 ) , а модуль упругости стали, используемой в балке, составляет 200 ГПа (200000 Н / мм 2 ) . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
Максимальное напряжение в балке можно рассчитать
σ max = (150 мм) (6 Н / мм) (5000 мм) 2 / (8 (81960000 мм 4 ))
= 34.3 Н / мм 2
= 34,3 10 6 Н / м 2 (Па)
= 34,3 МПа
Максимальный прогиб балки можно рассчитать
δ макс = 5 (6 Н / мм) (5000 мм) 4 / (( 200000 Н / мм 2 ) ( 81960000 мм 4 ) 384)
= 2,98 мм
Расчет балки с равномерной нагрузкой — метрические единицы
- 1 мм 4 = 10 -4 см 4 = 10 -12 м 4 1 см 4 = 10 -8 м = 10 4 мм
- 1 дюйм 4 = 4.16×10 5 мм 4 = 41,6 см 4
- 1 Н / мм 2 = 10 6 Н / м 2 (Па)
Расчет балки с равномерной нагрузкой — Британские единицы
Пример — балка с равномерной нагрузкой, британские единицы
Максимальное напряжение в стальной широкополочной балке W 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, при равномерной нагрузке 100 фунтов / дюйм можно рассчитать как
σ max = y max q L 2 / (8 I)
= (6.25 дюймов) (100 фунтов / дюйм) (100 дюймов) 2 / (8 (285 дюймов 4 ))
= 2741 (фунт / дюйм 2 , psi)
Максимальное отклонение может рассчитывается как
δ max = 5 q L 4 / (EI 384)
= 5 (100 фунтов / дюйм) (100 дюймов) 4 / ((2
00 фунтов / дюйм
2 ) (285 дюймов 4 ) 384)= 0,016 дюйма
Балка, поддерживаемая на обоих концах — нагрузка в центре
Максимальный момент в балке с центральной нагрузкой, поддерживаемой с обоих концов :
M max = FL / 4 (3a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой на обоих концах:
σ max = y max FL / (4 I) (3b) 904 82
где
F = нагрузка (Н, фунт)
Максимальный прогиб можно выразить как
δ max = FL 3 / (48 EI) (3c)
Силы, действующие на концы:
R 1 = R 2
= F / 2 (3d)
Калькулятор балки с одним центром нагрузки — метрические единицы
Калькулятор балки с одним центром нагрузки — британская система мер Единицы измерения
Пример — балка с одной центральной нагрузкой
Максимальное напряжение в стальной широкополкой балке «W 12 x 35», 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, с центральной нагрузкой 10000 фунтов можно рассчитать как
σ max = y max FL / (4 I)
= (6.25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 дюймов 4 ))
= 5482 (фунт / дюйм 2 , psi)
Максимальный прогиб можно рассчитать как
δ макс = FL 3 / EI 48
= (10000 фунтов / дюйм) (100 дюймов) 3 / ((200 фунтов / дюйм
2 ) (285 дюймов 4 ) 48 )
= 0,025 дюйма
Некоторые типичные пределы отклонения по вертикали
- полное отклонение: пролет / 250
- отклонение при динамической нагрузке: пролет / 360
- консоли: пролет / 180
- балки деревянных перекрытий в домашних условиях: 330 (макс. 14 мм)
- хрупкие элементы: пролет / 500
- подкрановые балки: пролет / 600
Балка, поддерживаемая на обоих концах — эксцентричная нагрузка
Максимальный момент в балке с одиночной эксцентричной нагрузкой в точке нагрузки:
M макс = F ab / L (4a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой с обоих концов:
σ max = y max F ab / (LI) (4b)
Максимальный прогиб в точке нагрузки можно выразить как
δ F = F a 2 b 2 / (3 EIL) (4c)
Силы, действующие на концы:
R 1 = F b / L (4d)
R 2 = F a / L (4e)
Балка, поддерживаемая на обоих концах — две эксцентриковые нагрузки
Максимальный момент (между нагрузками) в балке с двумя эксцентрическими нагрузками:
M max = F a (5a)
Максимальное напряжение
Максимальное напряжение в балке с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах:
σ max = y max F a / I (5b)
Максимум прогиб в точке нагрузки можно выразить как
δ F = F a (3L 2 — 4 a 2 ) / (24 EI) (5c)
Силы, действующие на концы:
R 1 = R 2
= F (5d)
Вставьте балки в свою модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Балка, поддерживаемая на обоих концах — трехточечная нагрузка
Максимальный момент (между нагрузками) в балке с тремя точечными нагрузками:
M max 90 087 = FL / 2 (6a)
Максимальное напряжение
Максимальное напряжение в балке с тремя точечными нагрузками, поддерживаемыми с обоих концов:
σ max = y max FL / (2 I) ( 6b)
Максимальный прогиб в центре балки можно выразить как
δ F = FL 3 / (20.22 EI) (6c)
Силы, действующие на концы:
R 1 = R 2
= 1,5 F (6d)
Нагрузки на балку — Калькулятор опорной силы
Онлайн-калькулятор опорной силы балки
Калькулятор ниже можно использовать для расчета опорной силы — R 1 и R 2 — для балок с 6 асимметричными нагрузками.
Длина балки (м, фут)
Усилие F1 (Н, фунт f ) расстояние от R 1 (м, фут)
Усилие F2 (Н, фунт ) f ) расстояние от R 1 (м, фут)
Сила F3 (Н, фунт f ) расстояние от R 1 (м, фут)
Сила F4 ( Н, фунт f ) расстояние от R 1 (м, фут)
Сила F5 (Н, фунт f ) расстояние от R 1 (м, фут)
Сила F6 (Н, фунт f ) расстояние от R 1 (м, фут)
Для балансира, нагруженного грузами (или другими нагрузочными силами), силы реакции — R — на опорах равно сил нагрузки — F . Баланс сил можно выразить как
F 1 + F 2 + …. + F n = 1 + R 2 (1)
где
F = усилие от нагрузки (Н, фунт f )
R = сила от опоры (Н, фунт f )
Дополнительно для балки в балансе алгебраическая сумма моментов равно нулю .Баланс момента можно выразить как
F 1 a f1 + F 2 a f2 + …. + F n a fn = R a r1 + R a r2 (2)
где
a = расстояние от силы до общей точки отсчета — обычно расстояние до одной из опор (м, футы)
Пример — A балка с двумя симметричными нагрузками
A Длинная балка длиной 10 м с двумя опорами нагружена двумя равными и симметричными нагрузками F 1 и F 2 , каждая 500 кг .Опорные силы F 3 и F 4 можно рассчитать
(500 кг) (9,81 м / с 2 ) + (500 кг) (9,81 м / с 2 ) = R 1 + R 2
=>
R 1 + R 2 = 9810 N
= 9,8 кН
Примечание! Нагрузка от веса груза — м — составляет мг Ньютона — где г = 9.81 м / с 2 .
При симметричных и равных нагрузках опорные силы также будут симметричными и равными. Используя
R 1 = R 2
, приведенное выше уравнение можно упростить до
R 1 = R 2 = (9810 N) / 2
= 4905 N
= 4,9 кН
Связанные мобильные приложения из Engineering ToolBox
— бесплатные приложения для автономного использования на мобильных устройствах.
Пример — балка с двумя несимметричными нагрузками
A Длинная балка длиной 10 м с двумя опорами нагружена двумя нагрузками, 500 кг расположен 1 м от конца ( R 1 ) , а другая нагрузка 1000 кг расположена 6 м от того же конца. Баланс сил можно выразить как
(500 кг) (9,81 м / с 2 ) + (1000 кг) (9,81 м / с 2 ) = 1 + R 2
=>
R 1 + R 2 = 14715 N
= 14.7 кН
Алгебраическая сумма моментов (2) может быть выражена как
(500 кг) (9,81 м / с 2 ) (1 м) + (1000 кг) (9,81 м / с 2 ) (6 м) =? R 1 (0 м) + R 2 (10 м)
=>
R 2 = 6377 (N)
= 6,4 кН
F 3 можно рассчитать как:
R 1 = (14715 Н) — (6377 Н)
= 8338 N
= 8.3 кН
Вставьте балки в модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Простой калькулятор балок | calcresource
Предпосылки
Оглавление
Введение
Балка с простой опорой — одна из самых простых конструкций. У него всего две опоры, по одной с каждой стороны. Одна штифтовая опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободное вращение вокруг них.Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя свободному горизонтальному перемещению препятствует другая опора.
Удаление любой из опор или установка внутреннего шарнира приведет к тому, что балка с простой опорой перейдет в механизм, то есть тело перемещается без ограничений в одном или нескольких направлениях. Очевидно, это нежелательно для несущей конструкции. Следовательно, балка с простой опорой не обеспечивает избыточности с точки зрения опор. Если произойдет локальный сбой, вся конструкция рухнет.Эти типы структур, которые не предлагают избыточности, называются критическими или детерминантными структурами. Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией .
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Обычно для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M.Для балки с простой опорой, которая несет только поперечные нагрузки, осевая сила всегда равна нулю, поэтому ею часто пренебрегают. Результаты расчетов на странице основаны на следующих предположениях:
- Материал однороден и изотропен (другими словами, его характеристики одинаковы во всех точках и в любом направлении)
- Материал линейно эластичный
- Нагрузки прикладываются статично (они не меняются со временем)
- Поперечное сечение одинаково по всей длине балки
- Прогибы небольшие
- Каждое поперечное сечение, которое изначально является плоским, а также перпендикулярно продольной оси, остается плоской и перпендикулярно отклоненной оси.Это тот случай, когда высота поперечного сечения намного меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).
Последние два предположения удовлетворяют кинематическим требованиям теории пучка Эйлера-Бернулли, которая здесь также принята.
Условные обозначения
Для расчета внутренних сил и моментов при любом разрезе сечения балки необходимо условное обозначение. Здесь приняты следующие значения:
- Осевая сила считается положительной, когда она вызывает натяжение детали.
- Сила сдвига положительна, когда она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила хотя и не являются обязательными, но достаточно универсальны. Другой набор правил, если следовать им последовательно, также даст те же физические результаты.
Условные обозначения
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общий пролет балки
- R: опора реакция
- d: прогиб
- M: изгибающий момент
- V: поперечная поперечная сила
- \ theta: slope
Балка с простой опорой и равномерно распределенной нагрузкой
Нагрузка w распределяется по всему пролету балки с постоянной величиной и направление. 3)} {24 EI} 91 684
Балка с простой опорой и точечной силой в середине
Сила сосредоточена в одной точке, расположенной в середине балки.Однако на практике сила может распространяться на небольшую площадь, хотя размеры этой области должны быть существенно меньше длины пролета балки. В непосредственной близости от приложения силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только местное явление. По мере удаления от места расположения силы результаты становятся действительными в силу принципа Сен-Венана.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенной точечной силы P, приложенной в середине.2)} {16 E I} &, x> L / 2 \ end {align} \ right.
где:
\ строго {x} = L-x
Балка с простой опорой, с точечной силой в произвольном положении
Сила сосредоточена в одной точке в любом месте пролета балки. Однако на практике сила может распространяться на небольшую площадь. Однако, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки.В непосредственной близости от силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только локальное явление, и по мере удаления от места расположения силы расхождение результатов становится незначительным.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенной точечной силы P, приложенной на случайном расстоянии a от левого конца.
Балка с точечной нагрузкой в произвольном положении | |
|---|---|
| Количество | Формула |
| Реакции: | R_A = {Pb \ over L} над L} |
| Концевые уклоны: | \ theta_A = — \ frac {P b (L ^ 2-b ^ 2)} {6E IL} \ theta_B = \ frac {P a (L ^ 2-a ^ 2)} {6E IL} |
| Предельный изгибающий момент: | M_u = {Pab \ over L} |
| Предельное усилие сдвига: | V_u = \ left \ {\ begin {выровнено } & {Pb \ over L} &, \ textrm {if:} a \ le L / 2 \\ — & {Pa \ over L} &, \ textrm {if:} a> L / 2 \ end {выровнено} \верно. 3} {6EI} &, x> a \ end {align} \ right.2} {2 E I} &, x> a \ end {align} \ right. |
где: b = La \ строго {x} = Lx | |
Балка с простой опорой с точечным моментом
В этом случае момент накладывается на одну точку балки в любом месте пролета балки. С практической точки зрения, это может быть пара сил или элемент на кручение, соединенный из плоскости и перпендикулярно балке.
В любом случае область приложения момента должна распространяться на небольшую длину луча, чтобы ее можно было успешно идеализировать как сосредоточенный момент в точке.Хотя в непосредственной близости от области применения ожидается, что результаты, предсказанные с помощью классической теории пучка, будут неточными (из-за концентраций напряжений и других локализованных эффектов), по мере того, как мы удаляемся, предсказанные результаты полностью верны, как заявил Святой -Венантный принцип.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенного точечного момента M, приложенного на расстоянии a от левого конца. 2 )} {6E IL}
где:
b = La
\ строго {x} = Lx
Балка с простой опорой и треугольной нагрузкой
Нагрузка распределяется по всему пролету балки, однако ее величина не константа, но изменяется линейно, начиная от нуля на левом конце до своего пикового значения w_1 на правом конце. Размеры w_1 — сила на длину. Общее количество силы, приложенной к балке, равно W = {1 \ over2} w L, где L — длина пролета.
Ориентация треугольной нагрузки важна! Формулы, представленные в этом разделе, были подготовлены для случая восходящей нагрузки (слева направо), как показано на схеме. Для нисходящей нагрузки вы можете отразить балку так, чтобы ее левый конец (точка A) был наименее нагруженным. Ось x и все результаты также будут отражены.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при линейно изменяющейся (треугольной) распределенной нагрузке, восходящей слева направо.4} {24EIL}
где:
C = \ sqrt {15- \ sqrt {120}} \ left (\ sqrt {15} + \ sqrt {50} \ right) \ приблизительно 22.01237
Балка с простой опорой и трапецеидальной нагрузкой
Нагрузка распределяется по всему пролету балки и имеет линейно изменяющуюся величину, начиная с w_1 на левом конце и заканчивая w_2 на правом конце. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L \ over2} (w_1 + w_2), где L — длина пролета.
Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).
В следующей таблице представлены формулы, описывающие статический отклик простой балки при переменной распределенной нагрузке трапециевидной формы. 3} {24EI}
где:
w_x = w_1 + {(w_2-w_1) x \ over L}
916 32Балка с простой опорой и трапециевидным распределением нагрузки типа плиты
Такое распределение нагрузки типично для балок по периметру плиты.Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах становится равной нулю. Размеры (\ w \) — сила на длину. Общее количество силы, приложенной к балке, равно W = w (La / 2-b / 2), где L — длина пролета, а a, b — длины с левой и правой стороны балки соответственно, где распределение нагрузки равно разная (треугольная).
В следующей таблице представлены формулы, описывающие статический отклик простой балки при трапецеидальном распределении нагрузки, как показано на схеме выше.3
Балка с простой опорой и частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть пролета балки с постоянной величиной w, в то время как оставшийся пролет разгружен. Размеры w — сила на длину. Общее количество силы, приложенной к балке, равно W = \ left (L-a-b \ right) w, где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки, соответственно.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при частично распределенной равномерной нагрузке.2} {2 E I} &, x \ ge L-b \ end {align} \ right.
где:
\ острый {x} = Lx
x_a = xa
L_w = Lab
Балка с простой опорой и частично распределенной трапециевидной нагрузкой
Часть нагрузки распределяется на часть пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет не нагружен. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L-a-b \ over2} (w_1 + w_2), где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки соответственно.
Значения w_1 и w_2 могут быть присвоены произвольно.


 м, кг
м, кг 26
26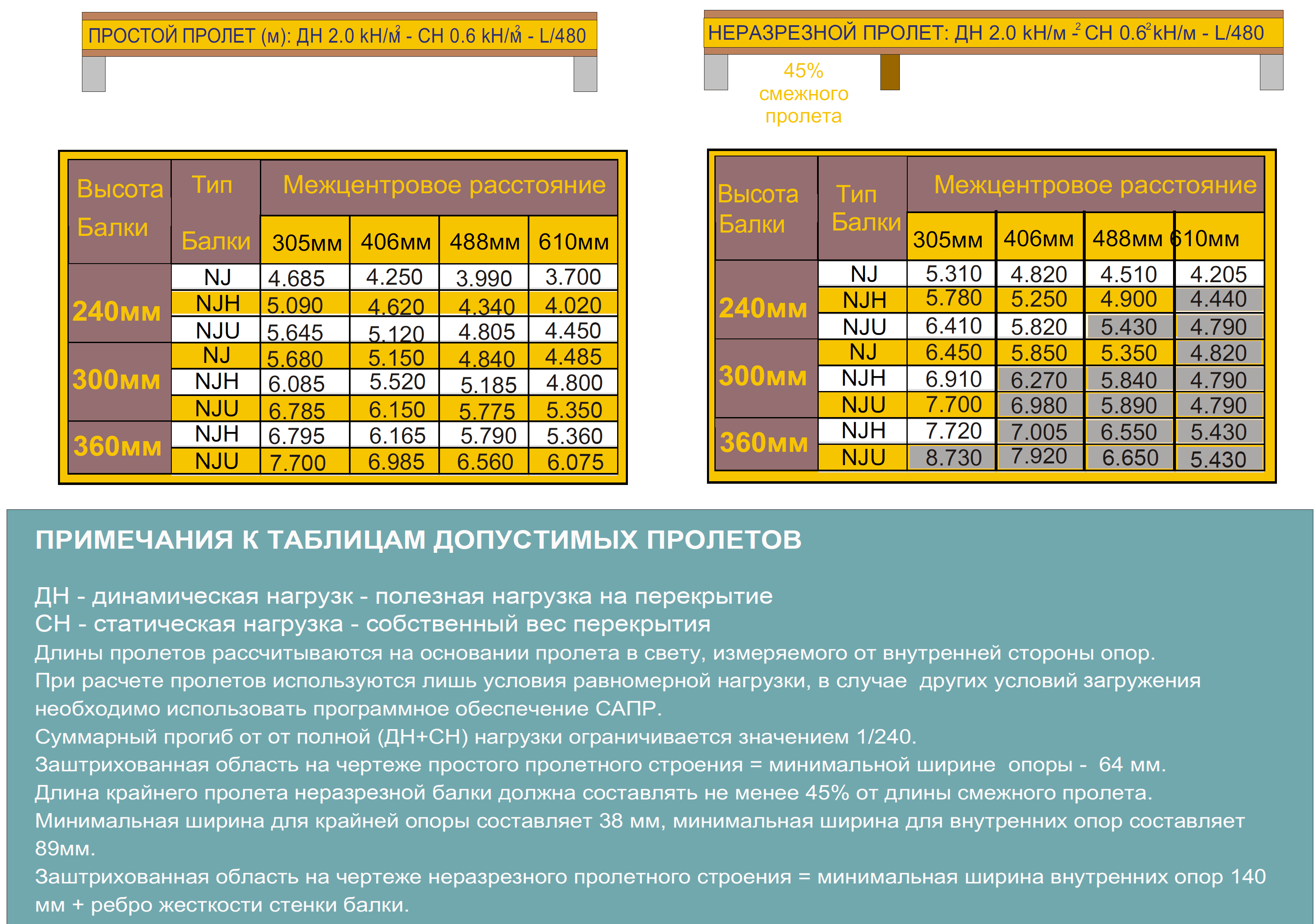 636
636 78
78 578
578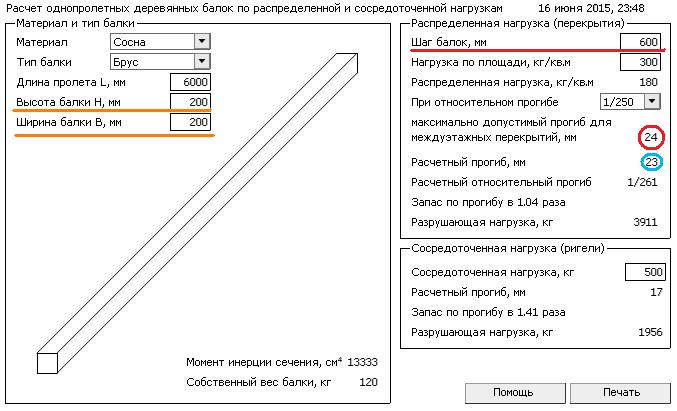 6
6 95
95 99
99 27
27 62
62 5
5