Как рассчитать общую площадь: Как посчитать площадь комнаты ПРОСТОЙ способ

Приведенная площадь квартиры: что значит, как рассчитать

Общая площадь, жилая, приведенная – что означают все эти слова и на какой параметр обращать внимание при проведении всевозможных сделок с недвижимостью? Мы решили рассказать вам, что такое приведенная площадь квартиры, каким образом она считается и когда вообще используется это значение?

Что называют приведенной площадью

Это понятие считается устаревшим и сегодня почти не используется, а раньше этот параметр учитывали для обозначения суммы платежей по коммунальным услугам. Что же это такое и где используется? В общую приведенную площадь включаются все имеющиеся помещения, в том числе балконы и кладовые.

Примечательно, что террасы, лоджии и балконы рассчитываются по заниженному коэффициенту, так как подобные помещения не жилые, а общедомовые. При этом каждый понимает, что балкон прибавляет удобства. Так почему же тогда у владельцев квартир с лоджиями/балконами коммунальные платежи должны быть такими же, как у людей без этих дополнительных удобств?

Все закономерно, но ведь на балконе или лоджии жить нельзя, а еще они не отапливаются, поэтому взимать за них плату, как с полноценных комнат, тоже неправильно. Помещения относят к приведенной площади, которая рассчитывается с особыми коэффициентами.

 

Чем общая площадь отличается от приведенной?

Как уже отметили, приведенная площадь квартиры – это термин, который почти не используют в современном мире, а вместо него применяют термин общей площади. Подобное положение дел вызывает путаницу среди не разбирающихся людей.

В зависимости от периода покупки квартиры, правоустанавливающая документация может содержать разные данные и формулировки. При этом общая площадь тоже обозначалась по-разному:

• Без лоджий с балконами, будто они отсутствуют (даже если по факту они есть).
• С учетом данных помещений, но их площадь рассчитана по коэффициентам. Соответственно, общая площадь совпадает с приведенной.
• С учетом габаритов балконов/лоджий в полном размере, то есть без коэффициентов.

Несмотря на все это, по факту отличий между общей и приведенной параметрами площади нет.

Как проводятся расчеты?

Общая приведенная площадь жилья просчитывается, как совокупность размеров всех имеющихся помещений, в том числе:

• кладовых;
• встроенных в стены шкафов;
• веранд и сушилок;
• балконов/лоджий и пр.

Но как считать этот показатель? Как было сказано, используются коэффициенты:

• балконы с террасами – 0,3;
• лоджии – 0,5;
• веранды – 0,8;
• совмещенные балкон с лоджией – 0,4.

Все эти данные регламентированы СНиП 31.01.2003. По закону, все эти помещения рассчитываются с понижающим коэффициентом в том случае, если они неотапливаемые.

 

Тонкости, о которых нужно знать

Жилплощадь отличается от общей и приведенной. К ней относят те помещения, в которых теоретически могут проживать люди: гостиные, спальни, детские комнаты. К общей также относят кухню, ванную и туалет, а по актуальному жилищному кодексу нашей странны формулировку «жилой площади» уже не используют.

Если изучить законодательство, вы найдете там формулировку, что общей площадью (ранее ее называли приведенной) является сумма всех жилых и нежилых помещений вместе с частями жилого дома.

Надеемся, мы помогли разобраться, как рассчитать жилую площадь квартиры из общей, что такое приведенная площадь, чем она отличается от других параметров и в каких случаях ее используют.

Если Вам необходимо рассчитать приведенную, общую площадь квартиры — обращайтесь к нам, в агентство недвижимости Вотчина. Наши сотрудники проведут рассчеты оперативно и грамотно, не оставив без внимания ни один нюанс. Компания существует на рынке недвижимости с 2001 года — за столь долгий срок мы накопили колоссальный опыт. Профессиональные риэлторы и юристы «Вотчины» окажут весь спектр специализированных услуг, в т.ч. одну из главных — осуществят проверку квартиры перед покупкой.

Посчитать общую площадь

Как же посчитать общую площадь индивидуального дома?

Площадь жилого дома — состоит из суммы площади всех частей такого помещения, жилого дома, включая площадь помещений вспомогательного использования, предназначенных для удовлетворения гражданами бытовых и иных нужд, связанных с их проживанием в жилом помещении, за исключением балконов, лоджий, веранд и террас.

Зачастую, возникает вопрос как же ведется расчет общей площади для индивидуального дома, так как во многих документах есть разночтения?

Проектирование индивидуальных домов ведется согласно СП 55.13330.2011 «ДОМА ЖИЛЫЕ ОДНОКВАРТИРНЫЕ».
Согласно СП 55.13330.2011 пункт 4.7 Правила подсчета площадей помещений, определения объема и этажности дома и количества этажей принимают по СП 54.13330 «Дома жилые многоквартирные». Смотрим там. Приложение В (обязательное) пункт В.1.1 Площадь жилого здания следует определять как сумму площадей этажей здания, измеренных в пределах внутренних поверхностей наружных стен.

 В площадь этажа включаются площади балконов, лоджий, террас и веранд, а также лестничных площадок и ступеней с учетом их площади в уровне данного этажа.

Проверяем в Жилищном Кодексе.

 

В соответствии с Жилищным кодексом статьей 15 «Объекты жилищных прав» пункт 5 «Общая площадь жилого помещения состоит из суммы площади всех частей такого помещения, включая площадь помещений вспомогательного использования, предназначенных для удовлетворения гражданами бытовых и иных нужд, связанных с их проживанием в жилом помещении, за исключением балконов, лоджий, веранд и террас».

  Норма статьи 15 пункт 5 носит императивный характер и не может быть изменена сторонами договорных отношений.

В соответствии со статьей 16 ЖК РФ «Виды жилых помещений» «1. К жилым помещениям относятся:
1) жилой дом, часть жилого дома;
2) квартира, часть квартиры;
3) комната».

Получается, что требования СП 54.13330 по расчету площадей жилого здания ПРОТИВОРЕЧАТ Жилищному кодексу.

С другой стороны в СП 54.13330 приведены требования для расчета многоквартирных жилых домов. Тогда разберемся, что же такое индивидуальный жилой дом?

 

Согласно СП 55.13330.2011 «ДОМА ЖИЛЫЕ ОДНОКВАРТИРНЫЕ» Приложению Б, термину 1.3

 Дом жилой одноквартирный – это дом, состоящий из отдельной квартиры (автономного жилого блока), включающий комплекс помещений, предназначенных для индивидуального и/или односемейного заселения жильцов, при их постоянном, длительном или кратковременном проживании (в т. ч. сезонном, отпускном и т.п.)
Соответственно наш дом – это отдельная квартира.

Рассмотрим правила для определения площади квартиры

, оно приводится в СП 54.13330.2011 «Дома жилые многоквартирные», Приложение В (обязательное)

В.2.1 Площадь квартир определяют как сумму площадей всех отапливаемых помещений (жилых комнат и помещений вспомогательного использования, предназначенных для удовлетворения бытовых и иных нужд) без учета неотапливаемых помещений (лоджий, балконов, веранд, террас, холодных кладовых и тамбуров). Площадь, занимаемая печью и (или) камином, которые входят в отопительную систему здания (а не являются декоративными), в площадь помещений квартиры не включается. Площадь под маршем внутриквартирной лестницы на участке с высотой от пола до низа выступающих конструкций лестницы 1,6 м и менее не  включается в площадь помещения, в котором размещена лестница. При определении площади комнат или помещений, расположенных в мансардном этаже, рекомендуется применять понижающий коэффициент 0,7 для площади частей помещения с высотой потолка от 1,6 м – при углах наклона потолка до 45о, а для площади частей помещения с высотой потолка от 1,9 м – от 45о и более.

Площади частей помещения с высотой менее 1,6 м и 1,9 м при соответствующих углах наклона потолка не учитываются. Высота помещения менее 2,5 м допускается не более чем на 50 % площади этого помещения. В.2.2 Общая площадь квартиры – сумма площадей ее отапливаемых комнат и помещений, встроенных шкафов, а также неотапливаемых помещений, подсчитываемых с понижающими коэффициентами, установленными правилами технической инвентаризации.

Таким образом, опять возникают следующие разночтения: в ЖК РФ общая площадь считается без балконов, лоджий и террас, а в СП 54.13330.2011 «Дома жилые многоквартирные» появляется два понятия:

Площадь квартиры, которая совпадает с понятием общая площадь ЖК РФ и вводится еще одно понятие:
Общая площадь квартиры, где плюсуется площадь балконов, лоджий и террас с понижающим коэффициентом.

Давайте рассмотрим еще один документ.
Согласно, Приказу Министерства экономического развития Российской Федерации (Минэкономразвития России) от 30 сентября 2011 г.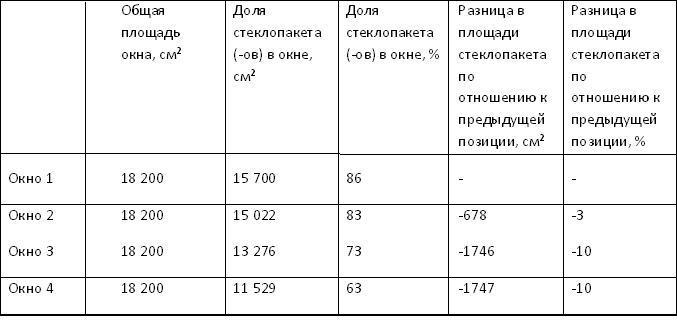

N 531 г. Москва

«Об утверждении Требований к определению площади здания, помещения» 

2. Значение площади и общей площади здания, помещения определяется в квадратных метрах с округлением до 0,1 квадратного метра, а значения измеренных расстояний, применяемые для определения площадей, — метрах с округлением до 0,01 метра.

III. Определение общей площади жилого помещения, жилого дома

6. Общая площадь жилого помещения, жилого дома состоит из суммы площади всех частей такого помещения, жилого дома, включая площадь помещений вспомогательного использования, предназначенных для удовлетворения гражданами бытовых и иных нужд, связанных с их проживанием в жилом помещении, за исключением балконов, лоджий, веранд и террас.

К площади помещений вспомогательного использования относятся площади кухонь, коридоров, ванн, санузлов, встроенных шкафов, кладовых, а также площадь, занятая внутриквартирной лестницей.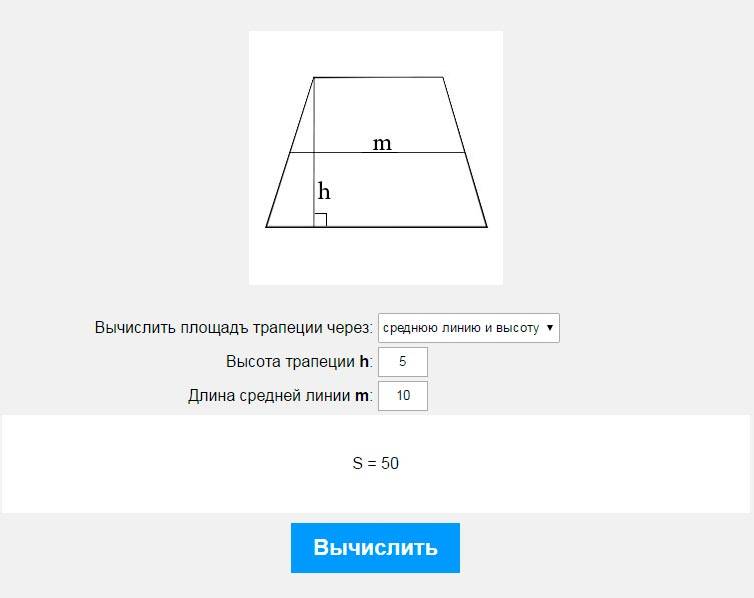

Измерение расстояний, применяемых для определения общей площади жилого помещения, жилого дома, производится по всему периметру стен на высоте 1,1 — 1,3 метра от пола.

При определении общей площади жилого помещения, жилого дома надлежит:

— площадь ниш высотой 2 метра и более включать в общую площадь помещений, в которых они расположены. Площади арочных проемов включать в общую площадь помещения, начиная с ширины 2 метра;

— площадь пола под маршем внутриквартирной лестницы, при высоте от пола до низа выступающих конструкций марша 1,6 метра и более, включать в общую площадь помещения, в котором расположена лестница;

— площадь, занятую выступающими конструктивными элементами и отопительными печами, а также находящуюся в пределах дверного проема, в общую площадь помещений не включать.

При определении общей площади помещений мансардного этажа учитывается площадь этого помещения с высотой от пола до наклонного потолка:

1,5 метра — при наклоне 30 градусов к горизонту;

1,1 метра — при 45 градусах;

0,5 метра — при 60 градусах и более.

При промежуточных значениях высота определяется по интерполяции.

Как измерить фасад для расчета облицовки

Для расчета сайдинга и аксессуаров, необходимых для отделки вашего дома, прежде всего, нужно знать:

1. Общую площадь фасада, включая площадь фронтона.
   
2. Площадь и глубину оконных и дверных проемов.
3. Периметр дома.
4. Высоту стен дома.
5. Периметр карнизного свеса и его глубину.

Чтобы получить эти значения сначала выполните замеры дома. Необходимо замерить стены, фронтоны, размеры и глубину оконных и дверных проемов. Удобнее всего измерять дом с помощью лазерной рулетки.

Советуем Вам нарисовать схему фасада в блокноте, и отметить на ней все полученные размеры. Это позволит в дальнейшем быстро и правильно рассчитать стоимость отделки.

В случае наличия архитектурного плана строительства дома, можно избежать дополнительных замеров.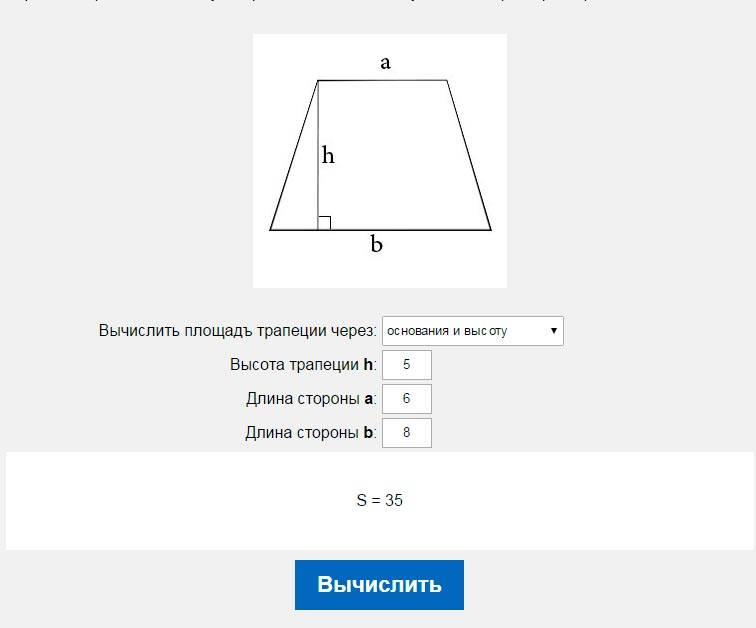 План строительства дома обязательно должен содержать все необходимые значения.

Итак, для измерения дома, нужно поделить на простые геометрические фигуры.

• Измерьте высоту и ширину стен.

Высота стены – это расстояние от цоколя до карнизного свеса. Ширина стены – это расстояние от угла до угла дома. Если же у Вас на доме не предусмотрен цоколь или вы хотите сделать отделку цоколя сайдингом, то измерять высоту стены необходимо от самого нижнего края стены.

• Измерьте высоту фронтонов.

Ширина фронтона как правило равна ширине стены и не требует дополнительных измерений. А вот высоту нужно обязательно измерить. Высота измеряется по центру от самой верхней части фронтона вниз до линии стыка фронтона со стеной.

Если у вашего дома мансардная крыша, то можно измерить высоту фронтона так же и высоту обычного треугольного фронтона, но при расчете площади, добавить к получившемуся числу 15%.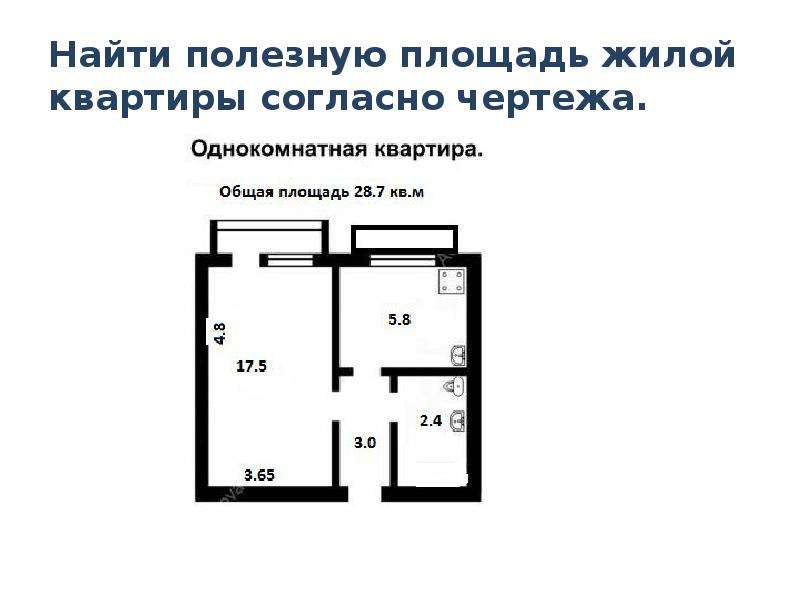

Если же вы хотите получить более точный расчет, то тогда измерьте фронтон, поделив его на два треугольника и прямоугольник.

• Измерьте высоту и ширину всех оконных и дверных проемов.

Высоту и ширину проемов необходимо измерять по внешней стороне наружного откоса от угла до угла.

Глубину проемов проще всего измерить по внутреннему углу наружного откоса от двери (окна) к улице. Измерьте глубину проемов по всем четырем углам. Выберите большее значение.

• Измерьте глубину оконных и дверных проемов.

Глубину проемов проще всего измерить по внутреннему углу наружного откоса от двери (окна) к улице. Измерьте глубину проемов по всем четырем углам. Выберите большее значение.

Теперь вы можете рассчитать все материалы, которые необходимы для отделки фасада вашего дома. Для этого воспользуйтесь простыми формулами расчета, представленными в следующем разделе.

Расчёт размеров и стоимости сайдинга

Калькулятор площади

Квадратная пирамида

h = высота
s = наклонная высота
a = длина стороны
e = длина боковой кромки
г = а / 2
В = объем
S _tot = общая площадь поверхности
S _шир.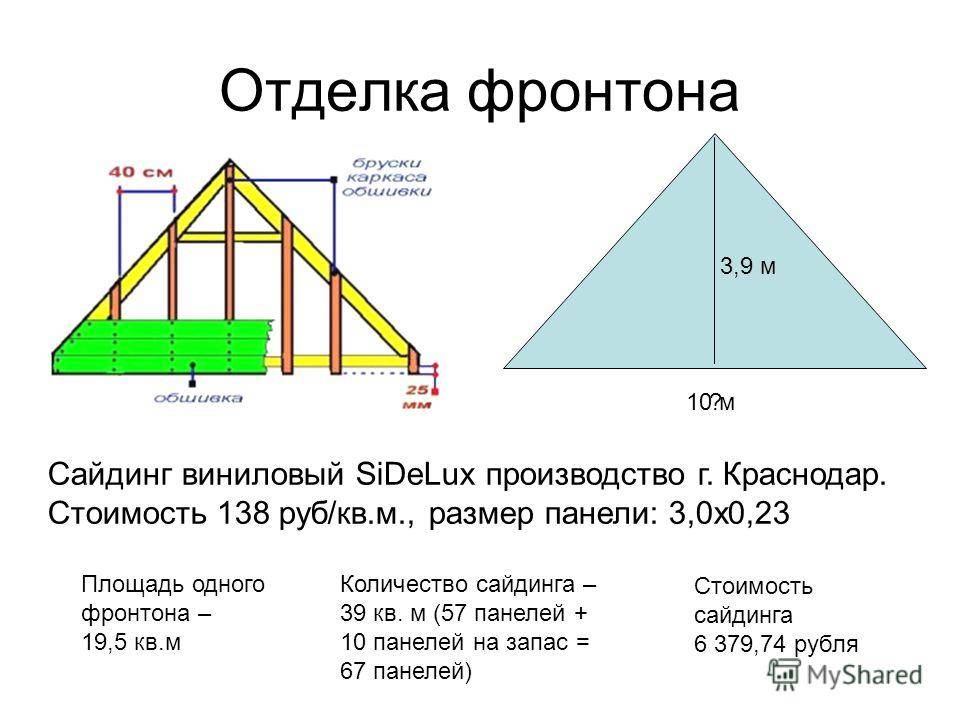 = площадь боковой поверхности
S _bot = площадь нижней поверхности

Рассчитывайте больше с
Калькулятор пирамид

Использование калькулятора

Онлайн-калькулятор для расчета площади поверхности геометрических тел, включая капсулу, конус, усеченную вершину, куб, цилиндр, полусферу, пирамиду, прямоугольную призму, сферу, сферический колпачок и треугольную призму

Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на вычисления.Единицы измерения указывают на порядок результатов, например футы, футы ² или футы ³ . Например, если вы начинаете с мм и знаете r и h в мм, ваши вычисления будут иметь V в мм ³ и S в мм ² .

Ниже приведены стандартные формулы для определения площади поверхности.

Формулы площади поверхности:

Площадь поверхности капсулы

• Объем = πr ² ((4/3) r + a)
• Площадь поверхности = 2πr (2r + a)

Площадь поверхности круглого конуса

• Объем = (1/3) πr ² ч
• Площадь боковой поверхности = πrs = πr√ (r ² + h ² )
• Площадь базовой поверхности = πr ²
• Общая площадь
  = L + B = πrs + πr ² = πr (s + r) = πr (r + √ (r ² + h ² ))

Площадь поверхности круглого цилиндра

• Объем = πr ² ч
• Площадь верхней поверхности = πr ²
• Площадь нижней поверхности = πr ²
• Общая площадь
  = L + T + B = 2πrh + 2 (πr ² ) = 2πr (h + r)

Площадь поверхности конической усадки

• Объем = (1/3) πh (r ₁ ² + r ₂ ² + (r ₁ * r ₂ ))
• Площадь боковой поверхности
  = π (r ₁ + r ₂ ) s = π (r ₁ + r ₂ ) √ ((r ₁ — r ₂ ) ² + h ² )
• Площадь верхней поверхности = πr ₁ ²
• Площадь базовой поверхности = πr ₂ ²
• Общая площадь
  = π (r ₁ ² + r ₂ ² + (r ₁ * r ₂ ) * s)
  = π [r ₁ ² + r ₂ ² + (r ₁ * r ₂ ) * √ ((r ₁ — r ₂ ) ² + h ² )]

Площадь поверхности куба

• Объем = a ³
• Площадь поверхности = 6a ²

Площадь поверхности полушария

• Объем = (2/3) πr ³
• Площадь изогнутой поверхности = 2πr ²
• Площадь базовой поверхности = πr ²
• Общая площадь поверхности = (2πr ² ) + (πr ² ) = 3πr ²

Площадь поверхности пирамиды

• Объем = (1/3) ² ч
• Площадь боковой поверхности = a√ (a ² + 4h ² )
• Площадь базовой поверхности = ²
• Общая площадь
  = L + B = a ² + a√ (a ² + 4h ² ))
  = a (a + √ (a ² + 4h ² ))

Площадь поверхности прямоугольной призмы

• Объем =
л / ч
• Площадь поверхности = 2 (lw + lh + wh)

Площадь поверхности сферы

• Объем = (4/3) πr ³
• Площадь поверхности = 4πr ²

Площадь поверхности сферической крышки

• Объем = (1/3) πh ² (3R — h)
• Площадь поверхности = 2πRh

Площадь поверхности треугольной призмы

Площадь верхней поверхности треугольной призмы по формуле

\ [A_ {top} = \ dfrac {1} {4} \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]

\ [A_ {top} = \ dfrac {1} {4} \ sqrt {\ begin {align} (a + & b + c) (b + ca) \\ & \ times (c + ab) (a + bc ) \ конец {выровнено}} \]

Площадь нижней поверхности треугольной призмы по формуле

\ [A_ {bot} = \ dfrac {1} {4} \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]

\ [A_ {bot} = \ dfrac {1} {4} \ sqrt {\ begin {align} (a + & b + c) (b + ca) \\ & \ times (c + ab) (a + bc ) \ конец {выровнено}} \]

Площадь боковой поверхности треугольной призмы Формула

\ [A_ {lat} = h (a + b + c) \]

Общая площадь поверхности треугольной призмы по формуле

\ [A_ {tot} = A_ {верх} + A_ {бот} + A_ {широта} \]

Калькулятор площади поверхности 📐 — Рассчитайте площадь поверхности куба, коробки, цилиндра, сферы, конуса.

..

Быстрая навигация:

1. Как рассчитать площадь поверхности тела?
2. Площадь поверхности куба
3. Площадь поверхности ящика
4. Площадь поверхности цилиндра
5. Площадь поверхности сферы
6. Площадь поверхности конуса
7. Площадь поверхности треугольной призмы

Как рассчитать площадь поверхности тела?

В зависимости от типа кузова существуют разные формулы и разная необходимая информация, необходимая для расчета площади поверхности (a.к.а. общая площадь ). Ниже приведены формулы для расчета площади поверхности наиболее распространенных типов телосложения.

При всех расчетах площади убедитесь, что все длины измеряются в одной и той же единице, например дюймы, футы, мм, см. Результатом нашего калькулятора площади всегда будет квадрат одной и той же единицы: квадратные футы, квадратные дюймы, квадратные метры, квадратные см, квадратные мм. пр.

Площадь куба

Формула площади поверхности для куба: 6 x сторона ² , как показано на рисунке ниже:

Этот расчет требует только одного измерения из-за симметричности куба. сторона ² — это поверхность одной из сторон, и поскольку куб имеет 6 равных сторон, умножение на 6 дает нам общую площадь поверхности куба.

Площадь ящика

Формула площади поверхности для прямоугольной коробки: 2 x (высота x ширина + ширина x длина + высота x длина) , как показано на рисунке ниже:

Поскольку прямоугольный ящик или резервуар имеет противоположные стороны, которые равны, мы вычисляем площадь каждой уникальной стороны, затем складываем их вместе и, наконец, умножаем на два, чтобы найти общую площадь поверхности.

Площадь цилиндра

Формула площади поверхности для цилиндра: π x диаметр x (диаметр / 2 + высота) , где (диаметр / 2) — радиус основания (d = 2 xr), поэтому можно записать его другим способом: π x радиус x 2 x (радиус + высота) . Изображение на рисунке ниже:

Площадь поверхности цилиндра — это высота, умноженная на периметр основания круга, плюс площади двух оснований, сложенные вместе.

Площадь поверхности сферы

Формула площади поверхности для сферы: 4 x π x (диаметр / 2) ² , где (диаметр / 2) — радиус сферы (d = 2 xr), поэтому можно записать ее по-другому: 4 x π x радиус ² . Наглядно на рисунке ниже:

Площадь поверхности сферы можно рассчитать, просто зная ее диаметр или радиус (диаметр = 2 x радиус). π — это, конечно, хорошо известная математическая константа, примерно равная 3.14159. Чтобы найти SA, просто умножьте 4 раза 3,14159 на квадрат радиуса.

Площадь конуса

Формула площади поверхности конуса с учетом его диаметра (или радиуса) и высоты равна π x (диаметр / 2) ² + π x (диаметр / 2) x √ ((диаметр / 2) ² + (высота ² )) , где (диаметр / 2) — радиус основания (d = 2 xr), поэтому можно записать его по-другому: π x радиус ² + π x радиус x √ (радиус ² + (высота ² )) , как показано на рисунке ниже:

Площадь поверхности конуса — одна из самых сложных, и именно здесь потребность в калькуляторе становится более очевидной.Вам нужно всего два измерения: диаметр основания и его высота, но исчисление более сложное, чем у большинства других простых тел.

Площадь поверхности треугольной призмы

Формула площади поверхности для треугольной призмы: 2 * (высота x основание / 2) + длина x ширина ₁ + длина x ширина ₂ + длина x основание , как показано на рисунке ниже:

Треугольная призма — это стопка треугольников, поэтому при вычислении площади оснований применяются обычные правила решения треугольников.

Площадь цилиндра

Площадь поверхности цилиндра может быть определена как общее пространство, занимаемое плоскими поверхностями оснований цилиндра и изогнутой поверхностью. Общая площадь цилиндра состоит из двух составляющих:

• изогнутая поверхность
• площадь плоской поверхности (двух плоских поверхностей)

В этом разделе мы обсудим, какова площадь поверхности цилиндра и как рассчитать общую площадь поверхности и площадь боковой поверхности цилиндра.Цилиндр — это трехмерный твердый объект, состоящий из двух круглых оснований, соединенных изогнутой гранью.

Какова площадь поверхности цилиндра?

Площадь поверхности цилиндра может быть определена как пространство, занимаемое плоской поверхностью основания цилиндра и изогнутой поверхностью цилиндра. Площадь поверхности цилиндра на самом деле является суммой площади круга, поскольку основание цилиндра представляет собой круг, и площадь криволинейной поверхности, которая представляет собой прямоугольник, равный длине высоты цилиндра и окружности основания как ширине.Площадь поверхности выражается как «количество» квадратных единиц (квадратных сантиметров, квадратных дюймов, квадратных футов и т. Д.).

Формула площади поверхности цилиндра

Формула площади поверхности цилиндра используется для определения площади поверхности, занимаемой основаниями цилиндра в пределах его границы и криволинейной поверхности цилиндра. Поскольку цилиндр имеет изогнутую поверхность, мы можем выразить как площадь изогнутой поверхности, так и общую площадь поверхности.Цилиндр имеет два вида площади поверхности:

.

• Общая площадь
• Площадь изогнутой поверхности

Если радиус основания цилиндра равен «r», а высота цилиндра равна «h», площадь поверхности цилиндра определяется как:

• Общая площадь поверхности, T = 2πr (h + r)
• Площадь криволинейной поверхности, S = 2πrh

Изогнутая поверхность цилиндра

Площадь изогнутой поверхности цилиндра — это площадь, покрытая изогнутой поверхностью.Формула для расчета площади криволинейной поверхности цилиндра имеет вид

.

Площадь криволинейной поверхности цилиндра = 2πrh
где,

• r = Радиус основания цилиндра
• h = высота цилиндра

Общая площадь цилиндра

Общая площадь поверхности цилиндра получается сложением площади двух оснований и площади изогнутой поверхности. Таким образом, формула для площади поверхности цилиндра имеет вид:
Общая площадь цилиндра = 2πr ² + 2πrh = 2πr (h + r)

где,

• r = Базовый радиус цилиндра
• h = высота цилиндра

Расчет площади поверхности цилиндра

Площадь любой формы — это пространство, занимаемое ею.Цилиндр имеет 2 плоские поверхности, которые обычно представляют собой круги, и изогнутую поверхность, которая открывается в виде прямоугольника. Рассмотрим цилиндр высотой «h» и круглое основание с радиусом «r». Давайте откроем цилиндр и посмотрим на это.

Итак, площадь цилиндра — это площадь двух окружностей, радиус основания которых равен ‘r’, и площадь прямоугольника, который представляет собой изогнутую поверхность.

Высота этого прямоугольника равна высоте цилиндра h , а длина этого прямоугольника равна длине окружности круга, то есть 2πr.Таким образом, площадь этого прямоугольника равна площади криволинейной поверхности цилиндра = 2πrh.

Также общая площадь цилиндра = 2πr ² + 2πrh = 2πr (h + r)

Как рассчитать площадь поверхности цилиндра?

Площадь поверхности цилиндра равна площади, занимаемой основаниями цилиндра в пределах его границы и криволинейной поверхности цилиндра. Следуя шагам, упомянутым ниже, мы можем найти площадь поверхности цилиндра.

• Шаг 1 : Обратите внимание на радиус основания «r» и высоту «h» цилиндра. Убедитесь, что у обоих одинаковые устройства.
• Шаг 2: Понять необходимость расчета площади криволинейной поверхности или общей площади поверхности в соответствии с данной ситуацией.
• Шаг 3 : Реализуйте формулу для площади криволинейной поверхности 2πrh или общей площади поверхности 2πr (r + h).
• Шаг 4 : Ответ в квадратных единицах единицы радиуса длины.

Теперь, когда мы знаем формулу и метод расчета площади поверхности цилиндра, давайте теперь разберемся, как ее вычислить, с помощью некоторых решенных примеров.

Часто задаваемые вопросы о площади поверхности цилиндра

Какова площадь поверхности цилиндра?

Площадь поверхности цилиндра определяется как общая площадь или область, покрытая поверхностью формы. Площадь поверхности цилиндра выражается в квадратных единицах, например м ² , ² , см ² , ярд ² и т. Д.

Как определить площадь поверхности цилиндра?

Площадь поверхности цилиндра можно определить, выполнив шаги, указанные ниже,

• Шаг 1: Запишите радиус основания «r» и высоту «h» цилиндра. Убедитесь, что единицы измерения совпадают.
• Шаг 2: Примените формулу, чтобы найти площадь поверхности цилиндра, равную
  . LSA цилиндра = 2πrh
  TSA цилиндра = 2πr (h + r)
• Шаг 3: Выразите ответ подходящей единицей измерения.

Какова формула для расчета площади поверхности цилиндра?

Формула для расчета общей площади поверхности цилиндра имеет вид: общая площадь поверхности цилиндра = 2πr (h + r), а площадь криволинейной поверхности цилиндра формула: площадь криволинейной / боковой поверхности цилиндра = 2πrh, где r — радиус основания, а h — высота цилиндра.

☛Также чек:

Как определить площадь поверхности цилиндра с открытым верхом?

Площадь поверхности цилиндра с открытым верхом может быть рассчитана путем определения площади основания и криволинейной поверхности.Таким образом, площадь цилиндра без верха может быть задана как площадь поверхности цилиндра с открытым верхом = πr (2h + r), где r — радиус основания, а h — высота цилиндра. .

Какова формула определения площади основания цилиндра?

Основание цилиндра круглой формы. Таким образом, формула для определения площади основания цилиндра имеет вид πr ² , где r — радиус основания цилиндра.

Как рассчитать площадь поверхности цилиндра с помощью калькулятора?

Площадь поверхности цилиндра может быть легко оценена или определена с помощью вычислителя площади поверхности цилиндра.Это самый быстрый метод, с помощью которого мы можем оценить площадь поверхности за несколько секунд. Чтобы использовать то же самое, нам нужно ввести значение конкретных параметров на экране калькулятора, таких как радиус, высота цилиндра. Попробуйте онлайн-калькулятор площади цилиндра Cuemath и получите ответы одним щелчком мыши. Ознакомьтесь с рабочими листами с площадью поверхности цилиндров, чтобы больше попрактиковаться.

Как определить изогнутую поверхность цилиндра?

Площадь криволинейной поверхности цилиндра задается по формуле: площадь криволинейной / боковой поверхности цилиндра = 2πrh, где r — радиус основания, а h — высота цилиндра.

Каким будет TSA цилиндра, если заданы площадь криволинейной поверхности и окружность основания?

TSA цилиндра, когда задана площадь криволинейной поверхности и длина окружности основания, составляет, (площадь криволинейной поверхности + площадь основания) = (2πrh + πr ² ) или 2πr (h + r), где ‘r’ — основание радиус, а h — высота цилиндра.

Площадь призмы

В площадь боковой поверхности призма — сумма площадей его боковых граней.

В общий площадь поверхности призмы представляет собой сумму площадей его боковых граней и двух его оснований.

Обычно, если «правая» или «наклонная» не упоминаются, можно предположить, что призма — это правая призма.

Общая формула для площади боковой поверхности правой призмы: L . S .А . знак равно п час куда п представляет периметр основания и час представляет высоту призмы.

Пример 1:

Найдите площадь боковой поверхности треугольной призмы с краями основания. 3 дюймы, 4 дюймов и 5 дюймы и высота 8 дюймы.

Периметр — это сумма оснований.

п знак равно 3 + 4 + 5 знак равно 12 дюймы

Боковая поверхность знак равно 12 ( 8 ) знак равно 96 дюймы 2

Общая формула для общая площадь поверхности правой призмы Т .S . А . знак равно п час + 2 B куда п представляет периметр основания, час высота призмы и B площадь основания.

В целом нет простого способа рассчитать площадь поверхности наклонной призмы. Лучше всего найти отдельно площади оснований и боковых граней и сложить их.

Пример 2:

Найдите общую площадь поверхности равнобедренной трапециевидной призмы с параллельными краями основания. 6 см и 12 см, ножки основания 5 см каждый, высота основания 4 см и высота призмы 10 см.

Периметр основания складывается из длин сторон.

п знак равно 6 + 5 + 12 + 5 знак равно 28 год см

Поскольку основание представляет собой равнобедренную трапецию, его площадь равна 1 2 час ( б 1 + б 2 ) .

B знак равно 1 2 ( 4 ) ( 6 + 12 ) знак равно 36 см 2

Т .S . А . знак равно п час + 2 B знак равно 28 год ( 10 ) + 2 ( 36 ) знак равно 280 + 72 знак равно 352 см 2

Формулы площади поверхности

Формулы площади поверхности

(Математика | Геометрия | Формулы площади поверхности)

( пи = = 3.141592 …)

Поверхность Формулы площади
В общем, площадь поверхности представляет собой сумму все области всех форм, которые покрывают поверхность объекта.

Куб | Прямоугольный Призма | Призма | Сфера | Цилиндр | Единицы

Примечание: «ab» означает «а», умноженное на «б». «а

² » означает «в квадрате», что то же самое, что «а» умножить на «а».

Будьте осторожны !! Количество единиц.Используйте одни и те же единицы для всех измерений. Примеры

Площадь поверхности куба = 6 а 2

(а — длина стороны каждый край куба)

Проще говоря, площадь куба — это площадь шести квадратов, которые накрой это. Площадь одного из них a * a, или ² . Поскольку эти все одинаковые, вы можете умножить одно из них на шесть, так что поверхность площадь куба в 6 раз больше квадрата одной из сторон.

Площадь поверхности прямоугольника Призма = 2ab + 2bc + 2ac

(a, b и c — длины трех сторон)

Проще говоря, площадь прямоугольной призмы равна площади шести прямоугольники, которые его покрывают. Но нам не нужно вычислять все шесть, потому что мы знаем, что верх и низ одинаковы, передняя и задняя — это то же самое, и левая и правая стороны одинаковы.

Площадь верха и низа (длины сторон a и в) = а * с. Поскольку их два, вы получаете 2ac. Передняя и задняя имеют длину стороны b и c. Площадь одного из них b * c, а там их два, поэтому площадь поверхности этих двух равна 2bc. Левая и правая сторона имеет длину сторон a и b, поэтому площадь поверхности одного из их это а * б. Опять же, их два, поэтому их общая площадь поверхности это 2ab.

Площадь поверхности любой призмы

(б — форма концов)

Площадь поверхности = Боковая площадь + Площадь двух концов

(Боковая площадь) = (периметр формы b ) * L

Площадь поверхности = (периметр формы b ) * L + 2 * (Площадь формы b )

Площадь поверхности сферы = 4 пи r 2

(r — радиус окружности)

Площадь поверхности цилиндра = 2 pi r 2 + 2 pi r h

(h — высота цилиндра, r — радиус вершины)

Площадь поверхности = Области сверху и снизу + Площадь сбоку

Площадь поверхности = 2 (Площадь верха) + (периметр верха) * высота

Площадь поверхности = 2 ( pi r ² ) + (2 pi r) * h

На словах проще всего представить банку.Площадь поверхности — это площади всех частей, необходимых для закрытия банки. Это верх, низ, и бумажная этикетка, которая оборачивается по центру.

Вы можете найти область вверху (или внизу). Это формула для площади круга ( пи r ² ). Поскольку есть и верх, и дно, умноженное на два.

Сторона похожа на этикетку банки. Если оторвать и положить плоский это будет прямоугольник.Площадь прямоугольника — это произведение с двух сторон. Одна сторона — это высота банки, другая — периметр круга, так как этикетка один раз оборачивается вокруг банки. Так площадь прямоугольника (2 пи r) * h.

Сложите эти две части вместе, и вы получите формулу поверхности. площадь цилиндра.

Площадь поверхности = 2 ( pi r ² ) + (2 pi r) * h

Совет! Не забывайте единицы измерения.

Эти уравнения дадут вам правильные ответы, если вы будете держать единицы прямо. Например — найти площадь поверхности куба со стороной 5 дюймов, уравнение:

Площадь поверхности = 6 * (5 дюймов) ²

= 6 * (25 квадратных дюймов)

= 150 кв. Дюймов

Площадь поверхности цилиндра: формула и примеры — стенограмма видео и урока

Определение площади поверхности цилиндра — Реальный мир

В видеоуроке мы узнали формулу для определения площади поверхности цилиндра A = 2 π r (r + h), где r — радиус круговых концов цилиндра, а h — высота цилиндра.Следующее упражнение покажет, как эта формула эквивалентна суммированию площадей трех плоских поверхностей.

Материалы

1) Банка (легче использовать банки из более тонкого материала)

2) Линейка

3) Кухонные ножницы или ножницы, достаточно острые, чтобы разрезать край банки.

4) Консервный нож

5) Калькулятор

6) Бумага и карандаш

7) Тяжелые книги

Инструкции

1) Установите банку на стол и с помощью линейки измерьте высоту банки.Постарайтесь быть максимально точными. Запишите высоту на бумаге и четко обозначьте ее как высоту.

2) Возьмите линейку и измерьте диаметр круглого конца банки. Помните, что диаметр — это отрезок прямой, который идеально делит круг пополам. Постарайтесь быть максимально точными. Напишите диаметр на бумаге и четко обозначьте его как диаметр.

3) Разделите диаметр пополам и обозначьте это значение как радиус.

4) Воспользуйтесь формулой из видеоурока.

А = 2 π r (r + h)

для расчета площади поверхности банки.Запишите результат и обозначьте его как площадь поверхности, заданную формулой.

5) Используйте консервный нож (или попросите кого-нибудь помочь вам), чтобы удалить оба круглых конца банки. Не тратьте зря пищу внутри — это отличное занятие, когда вам все равно нужно открыть банку.

6) Осторожно используйте ножницы / ножницы, чтобы разрезать оставшуюся «трубку» банки сверху вниз по максимально прямой линии.

7) Осторожно «разверните» «трубку», чтобы расплющить ее.Края могут быть острыми. Используйте тяжелые книги, чтобы выровнять банку — положите книги на развернутую банку, чтобы она была плоской.

8) После того, как «трубочка» банки сплюснута, она должна иметь вид прямоугольника. Используйте линейку, чтобы измерить длину и ширину этого прямоугольника, и запишите размеры, четко обозначив их.

9) Найдите площадь поверхности банки, сложив плоскую часть прямоугольника и два круглых конца. Помните, что площадь прямоугольника A = l * w (длина, умноженная на ширину), а площадь круга A = π r2.Используйте значения длины и ширины из шага 8 и значение радиуса из шага 3. Запишите общую площадь, сложенную вместе, и обозначьте ее как площадь поверхности банки, найденную путем добавления частей.

10) Сравните результат шага 4 и шаг 9. Сходны ли окончательные результаты?

Заключение

Формула площади поверхности цилиндра получается путем сложения трех плоских областей — площадей каждого круглого конца и площади прямоугольника, составляющего «трубку».»Результаты эксперимента должны показать, что эти значения (как при использовании формулы, так и при сложении частей) должны быть очень похожими. Они должны быть идентичными, однако небольшая погрешность измерения может привести к немного разным площадям поверхности — но при идеальном измерении результаты должно быть так же.

Как рассчитать площадь земли или участков неправильной формы

Если вы геодезист или владелец земли, на которой хотите рассчитать площадь земли, то вы попали в нужное место.У геодезиста или учащихся всегда возникают общие проблемы с определением площади неровной земли.

Если земля квадратная, прямоугольная, треугольная, то мы можем легко найти площадь земли, используя простую геометрическую формулу. Обсудим, как по порядку посчитать площадь всех типов земель.

Все участки или земля не имеют фиксированной геометрической формы, такой как треугольник, прямоугольник или квадрат. Таким образом, нам часто приходится сталкиваться с трудностями при расчете площади таких земель, которые не имеют фиксированной геометрической формы.

Давайте опишем и разберем все возможные типы и формы земель, которые мы обычно должны вычислить.

1) Участки треугольной формы или земельный участок

Такие земли встречаются редко, но это не значит, что вам не придется сталкиваться с этой проблемой. Вы, вероятно, можете получить эти типы земли на углу края дороги или поворотной точке. Итак, давайте вкратце решим эти типы проблем.

Q) Рассчитайте площадь данного треугольного участка земли со стороной 21 м, 13 м и 20 м соответственно.

Решение: —

Пусть, Заданная сторона треугольника будет,

(AB) = (a) = 21 метр

(AC) = (b) = 21 метр

(AB) = (c) = 21 метр

У нас,

Итак, сначала рассчитываем полупериметры = (a + b + c) / 2 = (20 + 21 + 13) / 2 = 27 м.

Полупериметр треугольника равен половине его периметра, т. Е. (Сумма их сторон).

Теперь, используя приведенную выше формулу, получаем,

Площадь треугольного участка земли (А)

Следовательно, таким образом мы можем рассчитать площадь земель треугольной формы.Теперь посчитаем площадь прямоугольных участков земли.

2) Участки прямоугольной формы или земельный участок

Эти типы земель часто встречаются во всех областях. Стороны земли, одна сторона которых равна их противоположной стороне, а другая сторона равна другой стороне, известны как прямоугольные земли.

Все стороны перпендикулярны друг другу, то есть под углом 90 градусов друг к другу. Давайте разберемся с помощью цифр и цифр, приведенных ниже.

Q) Рассчитайте площадь прямоугольной площадки, размеры которой указаны на рисунке ниже.

Решение. Здесь на рисунке две стороны равны 14 метрам, а две стороны — 8 метрам.

итак, пусть длина (L) = 14 метров и ширина (B) = 8 метров

У нас,

Итак, используя приведенную выше формулу, мы получаем,

Площадь = L X B = (14 X 8) = 112 м ²

Следовательно, таким образом мы можем рассчитать площадь земельных участков прямоугольной формы. А теперь посчитаем площадь участков или земли.

Также читается,

что такое счетчик строки

Как проверить качество цемента на участке

Конструкция септика

3) Квадратные участки или земельный участок

Эти типы земель также распространены во всех областях.вы получите форму земли в основном и почти прямоугольной или квадратной формы. Стороны земли, все стороны которых равны друг другу, известны как квадратные земли.

Все стороны перпендикулярны друг другу, то есть под углом 90 градусов друг к другу. Давайте разберемся с помощью цифр и цифр, приведенных ниже.

Q) Вычислите площадь квадратного участка земли, размеры которого указаны на рисунке ниже.

Решение, Здесь на рисунке все стороны равны и 8 метров.

итак, пусть длина (L) = 8 метров

У нас,

Используя формулу выше,

Площадь земли (A) = (8 X 8) м ² = 64 м ²

Таким образом, мы можем вычислить площадь земли квадратной формы. А теперь посчитаем площадь приусадебных участков или земельных участков.

4) Трапеция земля

Этот тип земли может быть регулярным или неправильным. Я описываю здесь все типы земель с примерами.Давайте обсудим всю землю с помощью фигуры и формулы для ее расчета.

A) Площадка с двумя сторонами, параллельными друг другу

Эти типы земель находятся на обочине дороги и, возможно, искусственно созданы для других целей. В этом типе земли две стороны параллельны друг другу, а две другие — нет. Давайте разберемся на примере.

Вы также можете рассчитать площадь над землей, разделив землю на две части в прямоугольнике и треугольнике, которые вы можете увидеть на рисунке зеленой линией.

После этого вы можете снова использовать формулу квадрата и треугольника относительно друг друга и получить общую площадь.

Надеюсь, вы поняли и можете рассчитать площадь этих земель. Давайте посмотрим на другой тип неровной земли, который вы обычно находили при обследовании. но не волнуйтесь, я также произведу нумерацию этой земли. так что давайте двигаться вперед.

B) Участки, не имеющие параллельных друг другу сторон

Этот тип земли чаще всего встречается в любом месте штата и страны.Это неровная земля. В этих типах земель все стороны отличаются друг от друга. а также они составляют разные углы друг друга.

Геодезистам приходится рассчитывать эти типы земель, поэтому часто возникает больше проблем с такими типами земель, чтобы рассчитать фактическую площадь. давайте разберемся с числовой и формулой для расчета площади земли.

Q) Рассчитайте площадь неровной земли, размер которой указан на рисунке ниже.

Решение,

Рассчитать эти типы земель очень просто.Чтобы узнать площадь этих типов земель, в первую очередь закопайте четыре колышка или рейки во всех уголках земли. После этого сделайте замеры со всех сторон земли. и имейте в виду, что вы должны измерить любой из диагональных участков.

Теперь, как вы можете видеть на рисунке, вся территория разделена на две части с синими диагоналями линий, и они имеют форму треугольников.

Вот и все, используйте формулу треугольной земли отдельно и сложите обе, чтобы получить общую площадь.разве это не легко?

А теперь перейдем к расчету,

В треугольнике ABD,

лет, BD (a) = 5 метров, AD (b) = 3 метра, AB (c) = 4 метра

Снова имеем

где S = (a + b + c) / 2 = (5 + 3 + 4) / 2 = 6 метров.

Итак, складывая все значения, получаем Площадь треугольника ABD,

= A ₁ = 6 м ²

Аналогично для треугольника BDC,

лет, DC (a) = 13 метров, BC (b) = 12 метров, BD (c) = 5 метров

где (S) = (a + b + c) / 2 = (13 + 12 + 5) / 2 = 15 метров.

Итак, подставив все значения, получаем Площадь треугольника BDC,

= 30 м ²

Таким образом, общая площадь земли стала,

= Площадь треугольника ABD и треугольника BDC

= А ₁ + А ₂

= (6 + 30) м ²

= 36 м ²

Следовательно, таким образом мы можем вычислить площадь земли неправильной формы.

Итак, ребята, я надеюсь, что эта статья « как рассчитать площадь земли » останется для вас полезной.