Как рассчитать куб доски формула: Сколько досок 6 метров в кубе? (таблица, формула, пример расчёта)

Формула для расчета количества доски пола в м3 и м2 | Статьи

Кремлев Андрей Александрович

начальник производства

Сегодня на рынке строительных материалов присутствует большое разнообразие вариантов для обустройства пола, однако самым популярным штучным изделием является доска из натуральной древесины.

Наличие в доме этого природного материала способствует возникновению неповторимой уютной атмосферы, ощущения покоя и благополучия.

Эко-стиль стал популярен не только в отделке дачи. Поклонниками натурального дерева давно стали и владельцы загородных особняков, городских квартир, офисных помещений.

Видео о том, как из простой доски пола сделать шикарное изделие

В связи с высокой востребованностью погонажных изделий потенциального покупателя интересуют цены на половую доску за м3, которую используют для напольных покрытий.

Деревянная доска применяется для обшивки:

• полов внутри дома;
• полов бань;
• закрытых веранд;
• закрытых беседок;
• закрытых летних пристроек;
• утепленных балконов.

Половая доска цена за куб, формула рассчета

Специалисту рассчитать цену доски пола за 1 куб не составляет особого труда, а вот заказчику эта задача покажется сложной. Но если вникнуть в суть формулы, стоимость половой доски сможет вычислить любой человек, прошедший школьный курс математики.

Фото 1. Доска пола лиственница АВ

Чтобы определить цены на половую доску штучно, нужно узнать количество панелей в одном кубическом метре.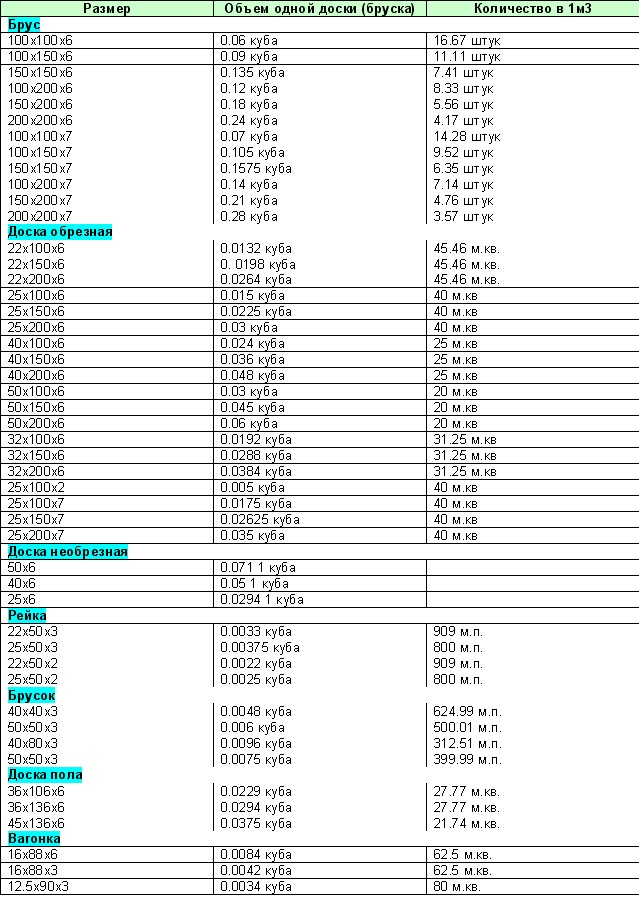

Проще всего сначала вычислить кубический объем (V) одной доски. Для этого необходимо знать следующие параметры (сантиметры и миллиметры следует перевести в метры):

1. толщину (высоту) изделий – H;
2. их длину – L;
3. ширину доски – B.

Далее необходимо использовать формулу: B×H×L=V, где V – это и есть объем одного изделия. Теперь 1 м3 делим на V, в результате чего получаем количество доски половой в кубе пиломатериала. Затем цену за куб делим на количество штук и получаем стоимость одной доски.

Фото 2. Доска пола Экстра

И наоборот: если известно, сколько стоит одна половая доска, цена за 1 куб определяется путем умножения этой цифры на количество штук в кубе.

Для тех, кто желает узнать стоимость за м2 существует другая формула

• 1м3 ÷ H = количество м2 доски в м3;
• B×L = размер доски в 1 м2;
• далее результат первого примера делим на результат второго (1м3 ÷ H) ÷ (B×L) = количество погонажных изделий в 1 м3.

Пример рассчета количества доски пола по формуле

Легче будет разобраться на примере. Возьмем доску с параметрами:

• H – 0,03 м;
• L – 6 м;
• B – 0,15 м.

Используем сначала первую формулу: 0,03×6×0.15=0,027 м3; 1÷0,027=37 досок в 1м3. Подставляем цифры во вторую формулу: (1÷0,03)÷(0.15×6)=37. Как видно, результат в обеих вариантах получается одинаковый.

Фото 3. Доска пола из сосны

Если шпунт оценивается продавцом поштучно, количество доски половой в кубе умножается на стоимость одной штуки и получается цена за куб.

Цена половой доски в прямой зависимости от сорта древесины

Стоимость пиломатериала зависит от качества половой доски и сорта древесины. Низкосортный материал не может оцениваться так же, как сорт доски «Экстра», «Премиум» или «A». Производство изделий высокого класса осуществляется, как правило, методом сращивания либо жесткой сортировки, в результате чего получается идеально гладкая поверхность, без сучков и темных пятен.

Фото 4. Доска из лиственницы в бане

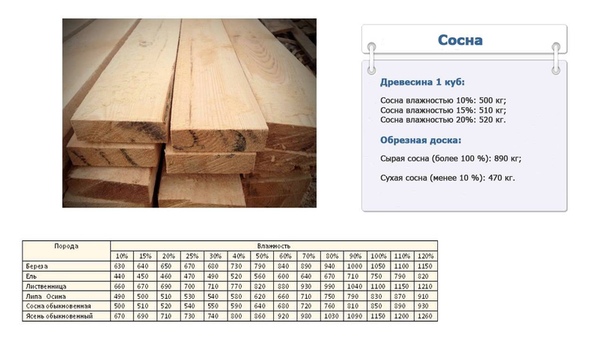
Древесный погонаж высших сортов используют для внутренней отделки. Для подсобных помещений вполне сгодится материал классов «B» и «C», стоимость которого гораздо ниже, чем у высококачественных аналогов. Выше всего на рынке ценится лиственница, самой дешевой является сосна.

Фото 5. Доска из сосны для пола

Влажность шпунта при продаже не должна превышать 16%. При влажности выше 16-18% доски в процессе высыхания деформируются, в результате чего нарушается эстетичность отделки, между половицами появляются некрасивые щели.

Если при выборе пиломатериалов у вас возникают сомнения, менеджеры компании «ЛесоБиржа» дадут вам профессиональную консультацию и помогут правильно произвести расчеты количества материала. Наши специалисты порекомендуют лучший вариант древесины с учетом всех условий строительного объекта.

Посмотрите, как мы можем

Как посчитать кубатуру досок обрезных и необрезных? (таблица, формула) |

Расчет кубатуры досок будет зависеть от того, обрезная (в том числе — строганная) это доска, или необрезная. В первом случае рассчитать кубатуру проще, поскольку пиломатериал имеет правильную геометрическую форму параллелепипеда. Кубатура необрезной доски – та, у которой бока необработаны, скорой, — высчитывается несколько иначе.

К счастью, расчет кубатуры доски провести несложно. В этом вам поможет либо таблица «Сколько досок в кубе», либо формула. Последний вариант надежней и точнее.

Расчет кубатуры досок обрезных

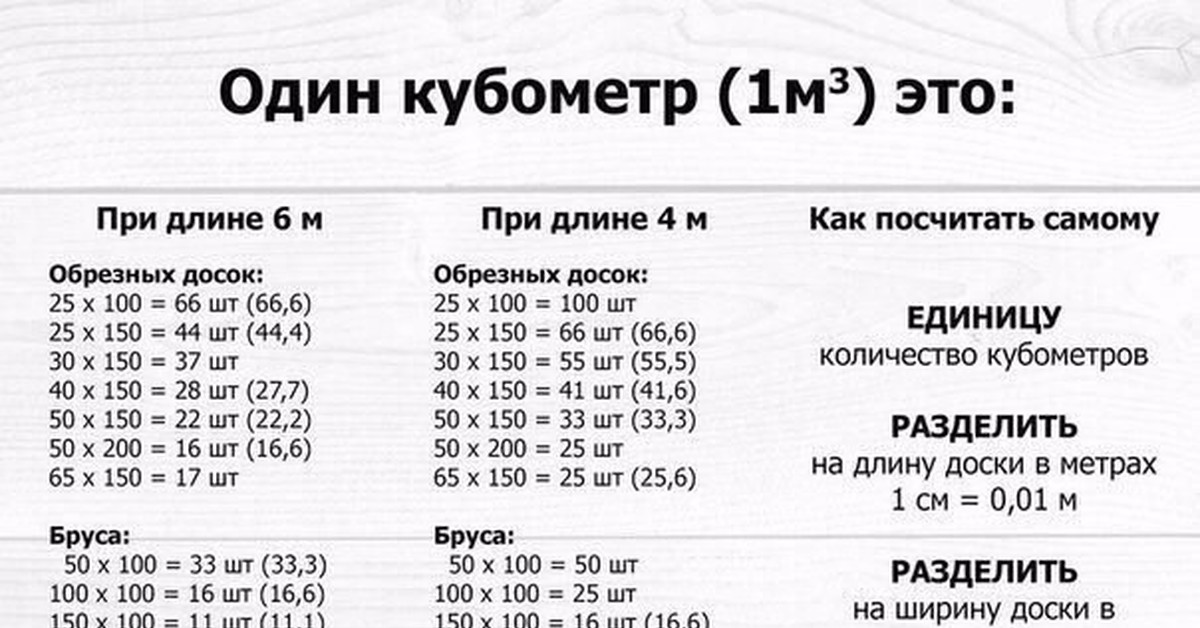
Сколько досок в кубе (таблица)

Из этой таблицы можно узнать ответы на такие популярные вопросы: как рассчитать кубатуру досок, сколько досок в кубе, сколько квадратных метров доски в кубе, сколько кубов в одной доске по самым популярным размерам.

Доска обрезная

Кубатура доски обрезной толщиной 50 миллиметров

Размер (мм)	м2  в 1 м3	Штук досок в 1 м3	Объем одной доски (в «кубах»)
100*6000	20	33	0,03
120*6000		27	0,036
150*6000		22	0,045
180*6000		18	0,054
200*6000		16	0,06
250*6000		13	0,075

 

Кубатура доски обрезной толщиной 40 миллиметров

Размер (мм)	м2  в 1 м3	Штук досок в 1 м3	Объем одной доски (в «кубах»)
100*6000	25	41	0,024
120*6000		34	0,0288
150*6000		27	0,036
180*6000		23	0,0432
200*6000		20	0,048
250*6000		16	0,06

 

Кубатура доски обрезной толщиной 32 миллиметра

Размер (мм)	м2  в 1 м3	Штук досок в 1 м3	Объем одной доски (в «кубах»)
100*6000	31	52	0,0192
120*6000		43	0,023
150*6000		34	0,0288
180*6000		28	0,0346
200*6000		26	0,0384
250*6000		20	0,048

Кубатура доски обрезной толщиной 30 миллиметров

Размер (мм)	м2  в 1 м3	Штук досок в 1 м3	Объем одной доски (в «кубах»)
100*6000	33	55	0,018
120*6000		46	0,0216
150*6000		37	0,027
180*6000		30	0,0324
200*6000		27	0,036
250*6000		22	0,045

 

Кубатура доски обрезной толщиной 25 миллиметров

Размер (мм)	м2  в 1 м3	Штук досок в 1 м3	Объем одной доски (в «кубах»)
100*6000	40	67	0,015
120*6000		55	0,018
150*6000		44	0,0225
180*6000		37	0,027
200*6000		33	0,03
250*6000		26	0,0375

 

Кубатура доски обрезной толщиной 20 миллиметров

Размер (мм)	м2  в 1 м3	Штук досок в 1 м3	Объем одной доски (в «кубах»)
100*6000	50	83	0,012
120*6000		69	0,0144
150*6000		55	0,018
180*6000		46	0,0216
200*6000		41	0,024
250*6000		33	0,03

 

Однако посчитать кубатуру обрезной доски более точно можно при помощи формулы.

Формула кубатуры доски обрезной такова:

a*b*l

где a – толщина доски

b – ее ширина

l – ее длина

Кубатуру доски высчитывают в кубометрах, поэтому перед тем, как посчитать кубатуру доски, все величины переводят из миллиметров в метры. Для примера возьмем доску «сороковку» 40*200*6000: толщина ее 40 мм (0,04 м), ширина 200 мм (0,02 м), длина – 6000 мм (6 м). Теперь проводим расчет кубатуры досок:

0,04*0,2*6=0,048 м³

То есть одна доска «сороковка» 100*6000 имеет кубатуру 0,048 м³. Чтобы определить, сколько досок в кубе, остается лишь разделить 1 на полученную сумму:

1/0,048=21 доска в 1 м³.

Расчет кубатуры досок необрезных

Необрезная доска отличается от обрезной тем, что по бокам она не обрабатывается, то есть одна сторона имеет неправильную форму, и точную ширину доски необрезной указать невозможно. С этим и связаны сложности с расчетом кубатуры необрезной доски, которые проще объяснить на конкретном примере.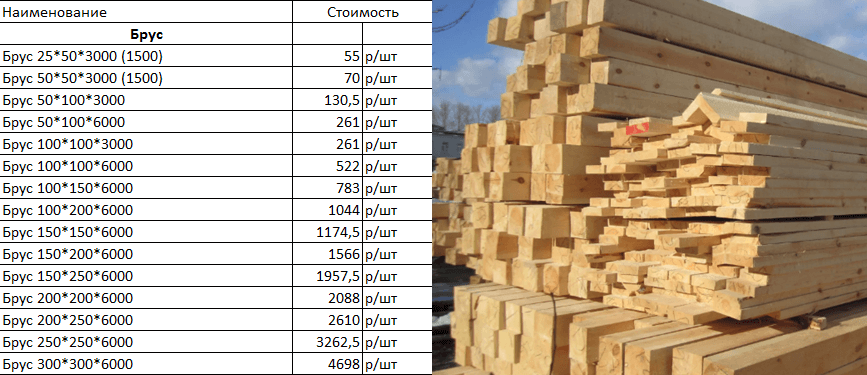

Доска необрезная

Предположим, вам необходимо обшить необрезной доской прямоугольное строение размерами 5*7 метров и высотой 4 метра. Доска у вас толщиной 50 миллиметров (0,05 м).

Для начала высчитывает отделочную площадь. Для этого (вспоминаем школу) умножаем периметр здания (две стороны по 5, две стороны по 7 – в итоге 24 метра) на высоту – 4 метра. Получаем 96 м².

Теперь площадь умножаем на толщину материала: 96*0,05=4,8 м³

Получается, что для обшивки ширина каждого обшивочного элемента практически не влияет на общую кубатуру. Точных таблиц кубатуры для досок необрезных нет и быть не может, поскольку неизвестно, с какой части бревна была вырезана доска, и какая у нее толщина с обеих сторон, но можно привести некие усредненные данные по кубатуре доски необрезной:

Толщина досок (длина – 6000 мм)	Средний объем одного элемента
25	0,0294
40	0,05
50	0,071

 

Вычисление кубатуры досок: о чем нужно помнить

Все фирмы-производители досок округляют цифры в ту сторону, которая выгодна для них. Возникает погрешность. В целом небольшая, но когда речь идет о сотнях кубов или нехватке досок для обшивки, вопрос становится ребром. Например, объем одной доски — 0,018 м³, а производитель округлил эту цифру до 0,02 м³. В итоге вместо ожидаемых 55 досок вы получите всего 50. Поэтому всегда уточняйте у продавцов данную информацию.

Надеемся, наша статья пролила свет на вопросы о том, сколько досок в кубе, как высчитать кубатуру доски, сколько досок в кубе и как не попасть впросак при покупке пиломатериалов.

 
Татьяна Кузьменко, член редколлегии Собкор интернет-издания «AtmWood. Дерево-промышленный вестник»

Как посчитать куб доски: пошаговая инструкция

Особенности правил продажи пиломатериалов достаточно сложны, поэтому даже контролирующие органы не всегда могут оценить точность отпуска такой продукции.

В отличие от иных видов товаров, материалы из древесины продают не на вес, не поштучно, а используют измерение кубометрами.

Как же посчитать, к примеру, куб доски? Достаточно заглянуть на страницы он-лайн журнала ProfiDom.com.ua и прочитать нижеследующую пошаговую инструкцию

Итак, нам понадобятся калькулятор и таблицы расчета объема пиломатериалов

Шаг 1. Некоторые производители поставляют в торговые организации готовые пакеты пиломатериалов, прикрепляя к ним бирку, где указаны точный объем и цена такого пакета. Осмотрите интересующую вас продукцию на предмет наличия такой бирки, это упростит расчеты. Впрочем, такая практика является исключением. Обычно измерение пиломатериалов производит кладовщик лесоторговой базы.

Шаг 2. Определите вид доски, которая вам необходима. Расчет кубатуры пиломатериалов зависит от степени ее обработки, вида и сортности. Так, в одном кубометре досок может содержаться разное количество обрезной и необрезной доски.

Шаг 3. Выберите метод расчета пиломатериалов. При вычислении объема пиломатериалов хвойных и лиственных пород используют два способа.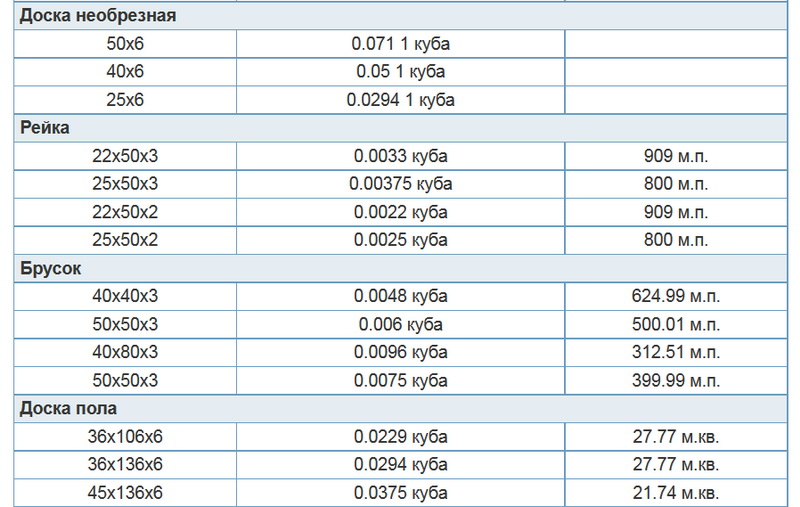 Первый метод – замер каждой доски и перемножение длины, ширины и толщины. Второй метод предполагает использование стандарта (кубатурника), предназначенного для вычисления объема обрезных пиломатериалов. В стандарте приводятся таблицы объема метра длины и одной штуки материала.

Шаг 4. Для примера, рассмотрим задачу, в которой требуется найти объем 50 обрезных досок шириной 125 мм, толщиной 22 мм, и длиной 4,5 м. По таблице найдите толщину пиломатериала, а затем на пересечении горизонтальной графы с требуемой шириной и вертикальной графы с соответствующей длиной найдите объем. Он будет равен 0,01238 куб. м. Теперь перемножьте найденный объем на число досок и получите искомый объем: 0,01238 х 50 = 0,619 куб. м.

Шаг 5. Измерение обычно производится не просто так, а для определения цены пиломатериалов при отпуске. В этом случае найдите по соответствующему прейскуранту розничную цену данного вида доски за один кубометр и определите стоимость всей партии, которую вы приобретаете. Правильность применения розничной цены вы можете проверить по папке ценообразования.

Расчет квадратуры и кубатуры пиломатериала

Ниже представлена таблица расчета объема пиломатериала стандартных сечений.
Таблица позволяет узнать, сколько в 1 кубе досок или бруса, а также какой объем имеет одна доска или брус.

 Формула расчета кубатуры пиломатериала: толщина x ширина x длина = объем

Наименование	Размер (т*ш*д, мм)	1 штука в м3	Кол-во штук в м3
Доска	25x100x6000	1 штука – 0. 015 м3	66.6 штук в м3
Доска	25x150x6000	1 штука – 0.0225 м3	44.4 штук в м3
Доска	25x180x6000	1 штука – 0.027 м3	37.03 штук в м3
Доска	25x200x6000	1 штука – 0.03 м3	33. 3 штук в м3
Доска	32x100x6000	1 штука – 0.0192 м3	52.08 штук в м3
Доска	32x150x6000	1 штука – 0.0288 м3	34.72 штук в м3
Доска	32x200x6000	1 штука – 0.0384 м3	26.04 штук в м3
Доска	40x100x6000	1 штука – 0. 024 м3	41.66 штук в м3
Доска	40x150x6000	1 штука – 0.036 м3	27.77 штук в м3
Доска	40x180x6000	1 штука – 0.0432 м3	23.14 штук в м3
Доска	40x200x6000	1 штука – 0.048 м3	20. 83 штук в м3
Доска	50X100X6000	1 штука – 0.03 м3	33.33 штук в м3
Доска	50x150x6000	1 штука – 0.045 м3	22.22 штук в м3
Доска	50x180x6000	1 штука – 0.054 м3	18.51 штук в м3
Доска	50x200x6000	1 штука – 0. 06 м3	16.66 штук в м3
Брус	100x100x6000	1 штука – 0.06 м3	16.67 штук в м3
Брус	100x150x6000	1 штука – 0.09 м3	11.11 штук в м3
Брус	100x180x6000	1 штука – 0.108 м3	9. 25штук в м3
Брус	100x200x6000	1 штука – 0.12 м3	8.33 штук в м3
Брус	150x150x6000	1 штука – 0.135 м3	7.41 штук в м3
Брус	150x180x6000	1 штука – 0.162 м3	6.17 штук в м3
Брус	150x200x6000	1 штука – 0. 18 м3	5.56 штук в м3
Брус	180x180x6000	1 штука – 0.1944 м3	5.14 штук в м3
Брус	200x200x6000	1 штука – 0.24 м3	4.17 штук в м3
Брусок	40x40x6000	1 штука – 0.0096 м3	104. 16 штук в м3
Брусок	40x50x6000	1 штука – 0.012 м3	83.3 штук в м3
Брусок	50x50x6000	1 штука – 0.015 м3	66.6 штук в м3

 

Сколько досок в 1 кубе?

Количество досок в кубе – параметр, учитываемый доставщиками пиленого лесоматериала. Распространителям это необходимо для оптимизации работы службы доставки, которая есть в каждом строймаркете.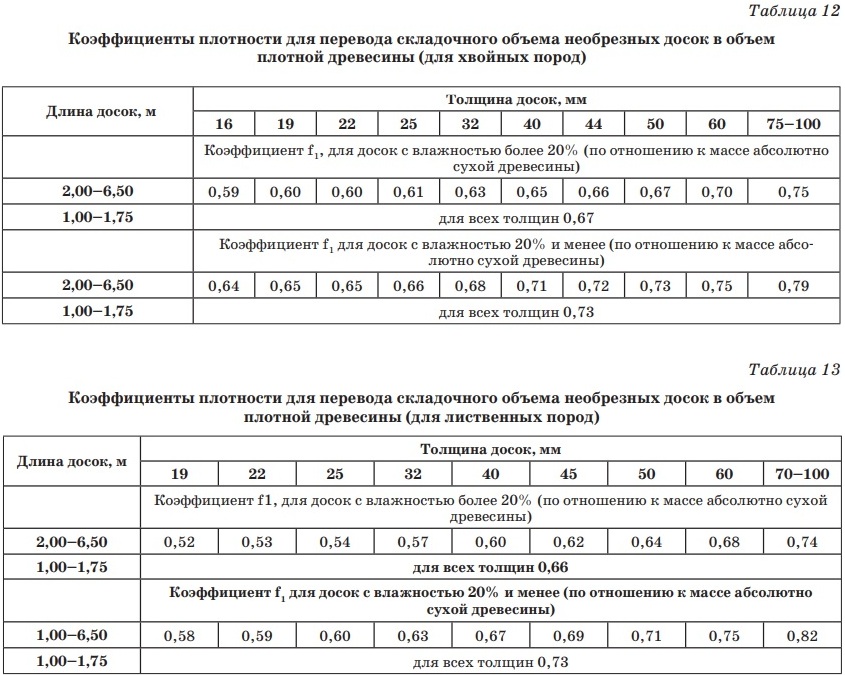

Что нужно учитывать при расчёте объёма?

Когда речь заходит о том, сколько весит конкретная порода дерева в кубометре, например, шпунтованной доски, то учитывают не только плотность той же лиственницы или сосны и степень просушки древесины. Не менее важно высчитать, сколько досок в кубометре этого же дерева – потребитель предпочитает знать заранее, с чем он столкнётся. Мало заказать и оплатить партию дерева – заказчику интересно будет выяснить, скольких человек нужно привлечь на разгрузку досок, как много времени займёт этот процесс, и каким образом сам клиент организует временное хранение заказанного деревоматериала, прежде чем тот весь уйдёт в предстоящее дело.

Для определения количества досок в кубометре используется простая формула, известная с начальных классов школы – «куб» делят на объём пространства, занимаемый одной доской. А чтобы вычислить объём доски, её протяжённость умножают на площадь сечения – произведение толщины на ширину.

Но если с обрезной доской расчёт прост и ясен, то необрезная вносит некоторые коррективы. Необрезная доска – элемент, боковины которого по длине не выравнивались на пилораме при заготовке данной разновидности продукции. Она может быть уложена немного нестандартно за счёт перепадов ширины – в том числе и «валетом» – разных сторон. Так как распущенный на доски ствол сосны, лиственницы или иного древовидного сорта имеет переменную толщину от прикорневой зоны до вершины, за основу перерасчёта берётся среднее его значение по ширине. Необрезная доска и горбыль (поверхностный слой, имеющий одну округлую сторону по всей длине) отсортировываются в отдельные партии. Так как длина и толщина необрезной доски одинаковы, а ширина значительно разнится, то распущенная необрезанная продукция также предварительно сортируется по разной толщине, потому что полоса, прошедшая по центру сердцевины, окажется значительно шире, чем аналогичная часть, не затронувшая эту сердцевину вообще.

Для предельно точного подсчёта количества необрезной доски применяется следующий метод:

1. если на конце ширина доски составила 20 см, а в начале (у основания) – 24, то среднее значение выбирается равным 22;

2. подобные по ширине доски раскладываются таким образом, чтобы изменение ширины не превышало 10 см;

3. длина досок должна сходиться один в один;

4. используя рулеточную или «угольниковую» линейку, вымеряют высоту всей стопки досок;

5. вымеряется ширина досок по середине;

6. результат умножается на нечто среднее между поправочными значениями от 0,07 до 0,09.

Значения коэффициента определяет воздушный просвет, оставленный неравномерной шириной досок.

Как посчитать кубатуру доски?

Итак, в каталоге продукции отдельно взятого магазина указано, к примеру, что имеется в продаже обрезная доска 40х100х6000. Эти величины – в миллиметрах – переводят в метры: 0,04х0,1х6. Правильно рассчитать поможет также перевод миллиметров в метры по следующей формуле после вычислений: в метре – 1000 мм, в квадратном метре уже содержится 1.000.000 мм2, а в кубическом – миллиард кубических миллиметров. Перемножив эти величины, получим 0,024 м3. Разделив кубометр на это значение, получим 41 целую доску, без разрезания 42-й. Целесообразно заказать чуть больше кубометра – и вам лишняя доска пригодится, и продавцу не нужно резать последнюю на куски, а затем искать покупателя на данный обрезок. С 42-й доской в данном случае объём выйдет равным чуть более кубометра – 1008 дм3 или 1,008 м3.

Кубатура доски рассчитывается и косвенным способом. Например, тот же заказчик сообщил объём заказа, равный ста доскам. В итоге 100 шт. 40х100х6000 равны 2,4 м3. Некоторые клиенты идут именно по такому пути – доска используется в основном для выстилания пола, потолочно-чердачного перекрытия, для возведения стропил и кровельной обрешётки, а это значит, что проще приобрести её расчётное количество поштучно – в некотором количестве – чем считать по кубометрам древесины.

Кубатура дерева получается как бы «сама собой» при точном расчёте на заказ без лишних переплат.

Сколько квадратных метров в кубе?

Закончив основные этапы стройки, переходят ко внутренней отделке. Не менее важно узнать, сколько квадратных метров покрытия уйдёт на один кубометр для обрезной и шпунтованной доски. Для обшивки стен, полов и потолка древесиной берётся расчёт покрытия кубометром материала конкретной площади. Длина и ширина доски умножаются друг на друга, затем полученная величина множится на их число в кубометре.

Например, для доски 25 на 150 на 6000 измерить площадь покрытия возможно следующим образом:

1. одна доска покроет 0,9 м2 площади;

2. кубометр доски покроет 40 м2.

Толщина доски здесь не имеет значения – она лишь приподнимет поверхность чистовой отделки на всё те же 25 мм.

Математические вычисления здесь опущены – приводятся только готовые ответы, проверить верность которых вы можете самостоятельно.

Таблица

Если под рукой сейчас нет калькулятора, то табличные значения помогут быстро отыскать требуемый номинал и определить его расход на площадь покрытия. Они отобразят численность экземпляров доски конкретного размера на «куб» древесины. В основном расчёт изначально опирается на протяжённость досок в 6 метров.

Пилить доски на 1 м уже нецелесообразно за исключением случаев, когда отделка уже закончена, а из остатков древесины делается мебель.

Доски метражом в 4 метра образуются при распиловке 1 штуки шестиметровых экземпляров на 4 и 2 м соответственно. Погрешность при этом составит не более 2 мм на каждую заготовку за счёт вынужденного измельчения слоя древесины, совпадающего с толщиной дисковой пилы на пилораме.

Это случится при однократном пилении по прямой, проходящей через точку-отметку, которую поставили в ходе предварительного замера.

Например, доска 100 на 30 мм протяжённостью 6 м – любой толщины – покроет собой 0,018 м2.

Возможные ошибки

Ошибки в исчислении могут быть следующими:

• взят не тот номинал среза доски;

• не учтена требуемая длина экземпляра продукции;

• выбрана не обрезная, а скажем, шпунтованная или не подвергавшаяся обрезанию по боковинам доска;

• миллиметры, сантиметры не переведены в метры изначально, перед расчётом.

Все эти ошибки – следствие спешки и невнимательности. Это чревато как недостачей оплаченного и подвезённого пильного леса (тёса), так и его перерасходом и возникшей переплатой. Во втором случае пользователь ищет, кому бы продать остатки древесины, нужды в которой больше нет – стройка, отделка и изготовление мебели окончились, а реконструкции нет и не предвидится в ближайшие, скажем, лет двадцать-тридцать.

Как правильно посчитать объём бревна?

Кубатурой бревна называют объем древесного материала, измеренный в кубических метрах. Эта величина используется в строительстве деревянных срубов для вычисления количества круглого леса. Определять кубатуру важно при продаже дров, где предусматривается оплата за каждый кубический метр дерева. Как посчитать объем круглого цилиндрического пиломатериала правильно?

Знать кубатуру дерева надо при покупке этого стройматериала, так как оплата производится за каждый метр кубический.

Существует несколько способов ориентировочной оценки кубатуры круглого леса или дров. Все наработанные методики используют данные измерения геометрических размеров и математические расчеты. Для замера строительных величин традиционно используется рулетка.

Расчет кубатуры занимаемого пространства

Наиболее простой способ заключается в определении кубического прямоугольного пространства, в котором сложен брус. Таким местом может быть кузов самосвала или сарай. Также можно калькулировать геометрические размеры поленницы, если она сложена в виде аккуратного прямоугольника.

Поскольку пространственная кубатура заполнена деревом не полностью, определяемая величина уменьшается с помощью коэффициента пустот. В строительных вычислениях считается, что коэффициент пустот равен 0,8. То есть 20% пространства занято воздушными пустотами, а 80% – деревом.

Кубический размер определяется следующим образом:

1. Измеряются длина, ширина и высота прямоугольного пространства.
2. Полученные величины перемножаются между собой, получается значение объема.
3. Полученное значение умножается на коэффициент 0,8, учитывающий ориентировочное количество пустот между круглыми бревнами.
4. Полученное значение принимают за искомый объем бревна.

Данный способ применяется для вычисления кубатуры разнородного по размерам кругляка или досок, дров.

Вернуться к оглавлению

Расчет объема отдельных бревен

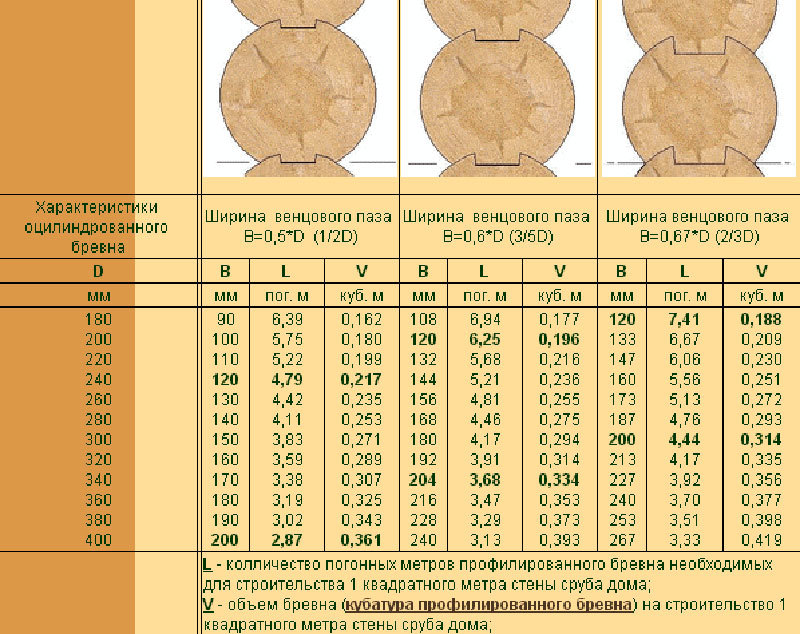
Рисунок 1. Измерение двух перпендикулярных диаметров в сечении бруса

Если круглый лес характеризуется одинаковой длинной бревен и близким диаметром, то можно посчитать объем выборочно 3-х брусов, свести их к средней расчетной величине и умножить ее на количество бревенчатого материала. В таком случае расчеты выполняются следующим образом:

1. Выбрать 3 любых бруса.
2. Измерить их диаметр и длину. Для удобства вычислений измерения произвести в метрах.
3. Рассчитать кубическое пространство, занимаемое каждым из кругляков по формуле:

V=Пи*R2*L,

где Пи – число, равное 3,14,

R – радиус, равный половине измеренного диаметра,

L – длина бруса.

4. Полученные значения 3-х кубатур круглого леса будут близки между собой. Их необходимо сложить и сумму разделить на 3. Таким образом, получим значение среднего объема одного бревна.
5. Далее умножаем полученную среднюю величину на количество заготовок в машине или хранилище.

Поскольку для строительства используются бревна близкого диаметра и стандартизованной длины, данный метод широко используется для оценки кубатуры строительного леса.

Если форма бруса слегка придавлена, его срез в сечении будет не круглым, а слегка овальным. Как тогда определить значение диаметра? Для этого измеряют размер 2-х перпендикулярных диаметров в сечении бруса: самого большого и самого маленького. Далее измеренные величины суммируют и делят на 2. Полученное значение будет средним диаметром, используемым в расчетах (рис. 1).

Вернуться к оглавлению

Расчет объема по таблицам

Расчет объема круглого леса с использованием таблиц заключается в измерениях диаметра и получении данных из готовых строительных таблиц.

Такие справочники содержат структурированную информацию, указывающую расход пиломатериала заданного диаметра на строительство 1 м² стены. Подобные таблицы являются результатом строительных расчетов и наработанной практики определения расхода пиломатериала. Поэтому они позволяют довольно точно оценить кубатуру строительного леса. Комплект таблиц, сведенных в единый стандартизированный документ, называется ГОСТом.

Чаще всего таблицы рассчитаны для оцилиндрованного бревна, у которого снят верхний слой и кора, поверхность выровнена до правильного цилиндра.

При желании можно использовать данные таблиц для определения количества необрезного дерева, делая поправку на возможные неточности. Ошибки полученных результатов будут связаны с изменением диаметра сечения кругляка на протяжении его длины.

Самостоятельный расчет количества круглого леса позволяет удостовериться в правильности определения цены продавцом. Экономически целесообразно проверить бригаду подрядчиков, проведя собственные ориентировочные расчеты расхода строительных бревен на возведение стен дома.

Сколько в кубе половой доски

Рассматриваемый материал задействуется в домах, квартирах. Преимуществами данного пиломатериала являются натуральность, экологичность, простота установки, длительность эксплуатации. Людям, которые планируют сделать ремонт, необходимо знать, сколько в кубе половой доски. 

Виды

Перед тем, как перейти к определению того, сколько половых досок в кубе, надо предварительно выяснить, какие виды материала бывают. Перед покупкой следует узнать, сколько стоит 1 м2 половой доски на нашем сайте.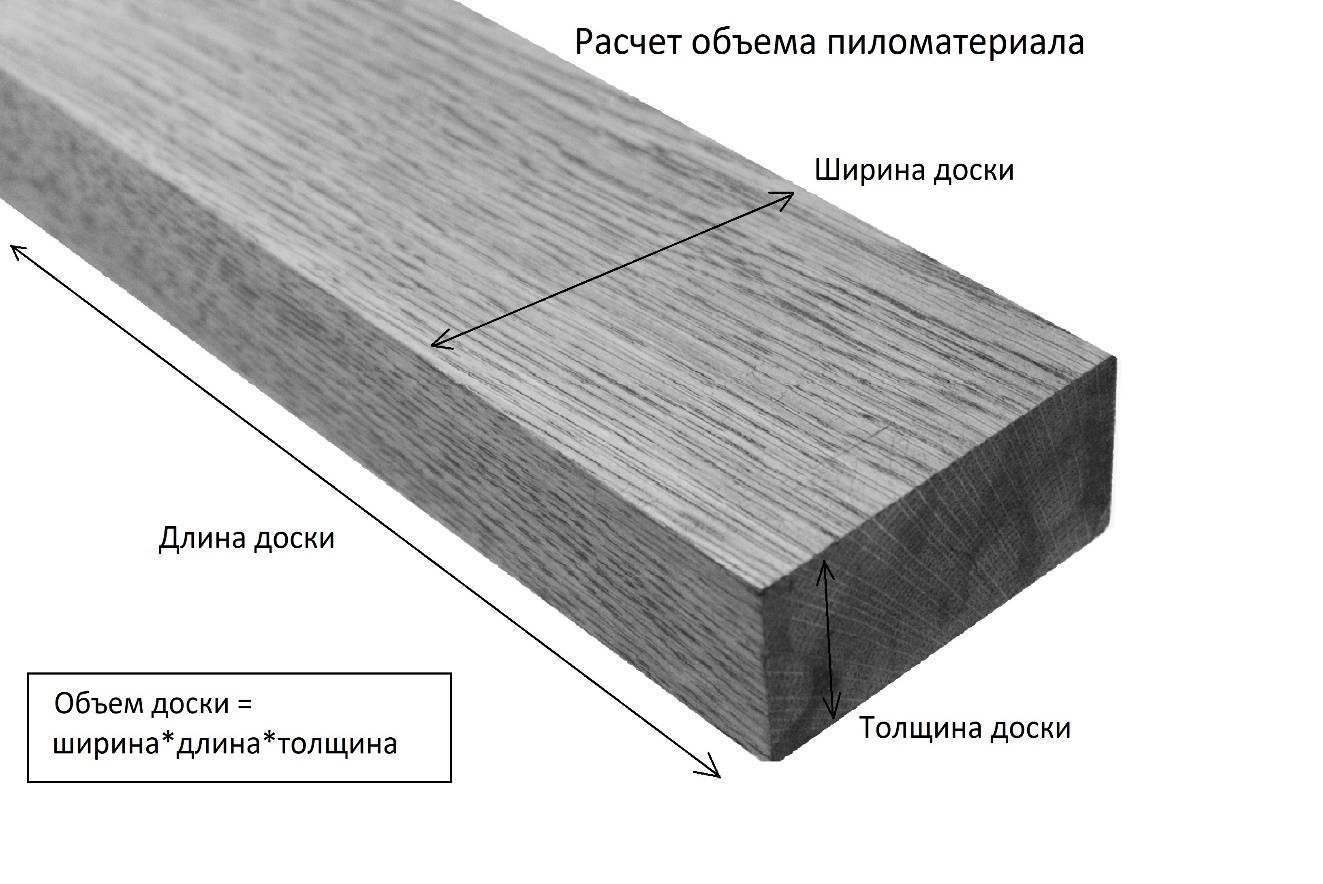 Для этого вы можете воспользоваться нашим прайс-листом https://ruslesmsk.ru/price-list/. Важно обратить внимание, что количество единиц вычисляется по одному и тому же принципу. Разновидность пиломатериала не играет роли в процессе вычисления.

Разновидности: 

1. Половая доска из лиственницы . 
2. Шпунтованная. 
3. Евро. 
4. Сосновая.

Куб доски половой: пример расчета

Стоимость куба половой доски у нас можно рассчитать самостоятельно. Выбирая сырье для укладки на лаги, нужно обращать внимание на самый важный критерий — толщину ламелей. Материал выпускается разной толщины: 20, 28 и 35 мм.

Толщина материала, мм	Расстояние между лагами, см	Покрываемая площадь пола одним кубометром доски, м2
20	30	50
28	40
35	60	28,5

Подсчет производится исходя из понятной формулы. Объем равняется произведению длин трех сторон. 

Символьная формула:

1 / (L*h*b) = N, где

h, b, L – высота, ширина, длина в метрах;

N – количество в 1 м³, штук.

Не нужно забывать, что подсчет по данной формуле носит приблизительный характер. Число может получиться дробное. Во время приобретения можно забрать объем пиломатериала, который является кратным целому и округленным в большую сторону. 

Наша компания предлагает клиентам такой материал, как половая доска цена за 1 куб которой доступна каждому человеку. Всегда следует покупать больше, чем необходимо. Это объясняется тем, что во время ремонта может быть использовано больше пиломатериала. Демократичная цена куба половой доски в нашем интернет-магазине позволяет запастись данным строительным материалом. 

Сколько стоит куб половых досок?

Для того чтобы узнать, сколько квадратных метров способен покрыть один кубический метр материала, следует округленное число досок в кубе умножить на площадь одной единицы (произведение длины на ширину). Рассчитать можно по такой формуле:

S = N * b * L, где

S – площадь в м², «зашиваемая» 1 м³ сырья.

В основном все расчеты половой доски производятся в квадратных метрах. Для удобства вычислений вы можете воспользоваться нашим калькулятором половой доски https://ruslesmsk.ru/calculator/

Как рассчитать объем куба: формула и практика — видео и стенограмма урока

Расчет объема

Чтобы найти объем любого куба, вам необходимо знать длину, ширину и высоту. Формула для определения объема умножает длину на ширину и высоту. Хорошая новость для куба заключается в том, что измерение каждого из этих измерений точно такое же. Поэтому длину любой стороны можно умножить в три раза. В результате получается формула: Объем = сторона * сторона * сторона.3

Результаты обучения

По завершении вы сможете:

• Сформулировать определение куба
• Напишите формулу для расчета объема куба
• Рассчитать объем куба

Формула куба — объяснение, свойства и решенные примеры

Что такое куб в математике?

Нас окружают разные вещи разной геометрической формы. Представьте себе детскую игру в кубики, игральные кости или кубик льда.Что вы видите общего среди всего этого? Все они имеют форму куба, не так ли? В этой статье мы изучим, что такое куб? Формула объема куба, формула площади куба, формула площади поверхности куба. Некоторые из распространенных примеров куба: Ice cube, Dice, Rubik’s Cube

Что такое куб?

Куб — это трехмерная фигура, состоящая из граней квадратной формы одинакового размера. Все углы куба пересекаются в 900. У куба 6 равных граней, и все грани имеют квадратную форму.У него 8 вершин и 12 равных ребер.

На рисунке ниже представлен куб, где l — длина, b — ширина, h — высота, а l = b = h. Длина, ширина и высота представляют края куба. И когда три ребра встречаются в точке, это называется вершиной.

[Изображение будет загружено в ближайшее время]

Свойства куба

1. Все грани куба имеют квадратную форму.

2. Все грани и кромки равны.

3. Углы куба прямые.

4. Каждая из граней встречается с другими соседними четырьмя гранями.

5. Каждая из вершин пересекает три грани и три ребра.

6. Противоположные друг другу кромки параллельны и также равны.

7. Все 12 диагоналей на поверхности имеют одинаковую величину

8. Все 4 внутренние диагонали равны

Площадь поверхности по формуле куба

Площадь поверхности — это площадь, рассчитанная для трех габаритный объект.Поскольку трехмерный объект состоит из двухмерных граней, площадь поверхности представляет собой сумму площадей всех граней фигуры. Следовательно, чтобы найти площадь поверхности 3D-объекта, мы должны добавить площадь всех его граней. Мы можем использовать базовую формулу площади для вычисления его граней, поскольку они представляют собой простые 2D-фигуры,

Например, куб имеет шесть граней. Следовательно, его площадь поверхности будет суммой площадей всех шести граней. Поскольку все стороны куба являются квадратами, мы можем выразить площадь поверхности куба как 6 x (Площадь квадрата)

В основном площадь поверхности можно классифицировать как:

Площадь изогнутой поверхности объекта равна площадь всех криволинейных поверхностей объекта.

Боковая поверхность объекта — это площадь всех граней объекта, за исключением области его основания и вершины. Для куба площадь боковой поверхности будет суммой площадей четырех сторон, т.е. 4 стороны.

Площадь боковой поверхности = 4 × (край) 2

Общая площадь поверхности — это площадь всех граней, включая основания.

Куб — это трехмерный объект, поэтому пространство, занимаемое кубом, будет трехмерным.

Куб ограничен шестью квадратными гранями, поэтому площадь поверхности будет вычисляться путем сложения площадей всех шести квадратных граней. Следовательно, площадь поверхности по формуле куба равна

Площадь поверхности куба = 6 (сторона) 2

Объем по формуле куба

Пространство, занимаемое трехмерным объектом, равно измеряется объемом этого объекта. Объем твердой фигуры является произведением трех измерений, поэтому объем выражается в кубических единицах.Предположим, что объем куба измеряется произведением его длины, ширины и высоты.

Внутренняя часть полого предмета может быть заполнена воздухом или жидкостью, которая принимает форму предмета. В таких случаях объем вещества, который может вместить внутренняя часть объекта, называется емкостью полого объекта. Таким образом, мы можем сказать, что объем объекта — это мера пространства, которое он занимает, а емкость объекта — это объем вещества, которое может вместить его внутреннее пространство.

А объем куба — это занимаемое им пространство. Объем формулы куба будет рассчитан как

Длина диагонали грани куба = √2 (край)

Длина диагонали куба Куб = √3 (край)

Решенные примеры

Пример 1: Найдите площадь поверхности куба, длина сторон которого равна 7 см.

Решение:

Заданная длина = край = 7 см

Мы имеем, Площадь поверхности куба = 6 (край) 2

= 6 × 72

= 6 × 49

= 294 см2

Пример 2: Сторона кубического ящика — 9м. Найдите объем кубической коробки.

Решение:

Дано, Сторона = a = 9м

По формуле объема куба мы знаем, что

V = a3

V = 9 x 9 x 9

V = 729 кв.м или 729m2

Quiz Time

1. Каков объем куба со стороной 11.5 см?

2. Если объем куба равен 343 см3, то какова мера края куба?

Калькулятор площади поверхности

Используйте калькуляторы ниже, чтобы вычислить площадь поверхности нескольких распространенных форм.

Площадь поверхности мяча

Площадь поверхности конуса

Площадь поверхности куба

Площадь поверхности цилиндрического резервуара

Площадь прямоугольного резервуара

Площадь поверхности капсулы

Площадь поверхности крышки

Для расчета укажите любые два значения ниже.

Площадь поверхности конической усадки

Площадь поверхности эллипсоида

Площадь квадратной пирамиды

Калькулятор связанных объемов | Калькулятор площади | Калькулятор площади поверхности тела

Площадь поверхности твердого тела — это мера общей площади, занимаемой поверхностью объекта.Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для получения более подробной информации о каждом отдельном объекте.

Сфера

Площадь поверхности (SA) сферы можно рассчитать по формуле:

SA = 4πr ²
где r — радиус

Ксаэль не любит ни с кем делиться шоколадными трюфелями.Когда она получает коробку трюфелей Lindt, она приступает к вычислению площади поверхности каждого трюфеля, чтобы определить общую площадь поверхности, которую она должна лизать, чтобы уменьшить вероятность того, что кто-то попытается съесть ее трюфели. Учитывая, что каждый трюфель имеет радиус 0,325 дюйма:

SA = 4 × π × 0,325 ² = 1,327 дюйм ²

Конус

Площадь поверхности круглого конуса может быть вычислена путем суммирования площадей поверхности каждого из его отдельных компонентов.«Базовая SA» относится к кругу, который содержит основание в замкнутом круговом конусе, в то время как боковая SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого из них, а также общая SA замкнутого кругового конуса показаны ниже:

основание SA = πr ²
боковая SA = πr√r ² + h ²
общая SA = πr (r + √r ² + h ² )
где r — радиус, а h — высота

Афина недавно проявила интерес к культуре Юго-Восточной Азии и особенно увлеклась конической шляпой, обычно называемой «рисовой шляпой», которая обычно используется в ряде стран Юго-Восточной Азии.Она решает сделать свое собственное и, будучи очень практичным человеком, не погрязшим в сентиментальности, достает свадебное платье своей матери из темных уголков гардероба, в котором оно находится. Она определяет площадь поверхности материала, необходимого для создания шляпы с радиусом 1 фут и высотой 0,5 фута, следующим образом:

боковой SA = π × 0,4√0,4 ² + 0,5 ² = 0,805 фута ²

Куб

Площадь поверхности куба может быть вычислена путем суммирования общих площадей его шести квадратных граней:

SA = 6a ²
где a — длина кромки

Энн хочет подарить своему младшему брату кубик Рубика на его день рождения, но знает, что у ее брата мало внимания и он легко разочаровывается.Она заказывает кубик Рубика, у которого все грани черные, и должна платить за настройку в зависимости от площади поверхности куба с длиной ребра 4 дюйма.

SA = 6 × 4 ² = 96 дюймов ²

Цилиндрический бак

Площадь поверхности закрытого цилиндра может быть вычислена путем суммирования общих площадей его основания и боковой поверхности:

база SA = 2πr ²
боковой SA = 2πrh
общая SA = 2πr (r + h) где r — радиус, а h — высота

У Джереми есть большой цилиндрический аквариум, в котором он купается, потому что он не любит душ или ванну.Ему любопытно, остывает ли его нагретая вода быстрее, чем в ванне, и ему нужно рассчитать площадь поверхности его цилиндрического резервуара высотой 5,5 футов и радиусом 3,5 фута.

всего SA = 2π × 3,5 (3,5 + 5,5) = 197,920 футов ²

Прямоугольный бак

Площадь поверхности прямоугольного резервуара равна сумме площадей каждой из его граней:

SA = 2lw + 2lh + 2wh
где l — длина, w — ширина, а h — высота

Банан, старшая дочь в длинной череде фермеров, выращивающих бананы, хочет преподать своей испорченной гнилой младшей сестре Банановый хлеб урок о надеждах и ожиданиях.Banana-Bread всю неделю настаивает на том, чтобы ей нужен новый набор ящиков для размещения ее новых фигурок Бэтмена. Таким образом, Банана покупает ей большой кукольный домик Барби с кухонной утварью ограниченного выпуска, духовкой, фартуком и реалистичными гниющими бананами для Бэтмена. Она упаковывает их в прямоугольную коробку таких же размеров, как выдвижной ящик, который нужен Banana-Bread, и ей нужно определить количество оберточной бумаги, которое ей нужно, чтобы завершить презентацию подарка — сюрприз размером 3 × 4 × 5 футов:

SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 футов ²

Капсула

Площадь поверхности капсулы может быть определена путем комбинирования уравнений площади поверхности для сферы и площади боковой поверхности цилиндра.Обратите внимание, что площадь поверхности оснований цилиндра не включена, поскольку она не составляет часть площади поверхности капсулы. Общая площадь поверхности рассчитывается следующим образом:

SA = 4πr ² + 2πrh
где r — радиус, а h — высота.

Горацио производит плацебо, которое призвано оттачивать индивидуальность человека, критическое мышление и способность объективно и логично подходить к различным ситуациям.Он уже протестировал рынок и обнаружил, что подавляющее большинство выборочной совокупности не проявляют ни одного из этих качеств и очень готовы купить его продукт, еще больше укрепляя свои черты, от которых они так отчаянно стремятся избавиться. Горацио должен определить площадь поверхности каждой капсулы, чтобы он мог покрыть их чрезмерным слоем сахара и обратиться к предрасположенным к сахару языкам населения при подготовке к следующему плацебо, которое «излечит» все формы сахарного диабета.Учитывая, что каждая капсула имеет r 0,05 дюйма и h 0,5 дюйма:

SA = 4π × 0,05 ² + 2π × 0,05 × 0,5 = 0,188 дюйма ²

Сферический колпачок

Площадь поверхности сферической крышки зависит от высоты рассматриваемого сегмента. Предоставленный калькулятор предполагает твердую сферу и включает основание крышки при расчете площади поверхности, где общая площадь поверхности является суммой площади основания и боковой поверхности сферической крышки.Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Учитывая два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, представленных в Калькуляторе объема. Уравнения площади поверхности следующие:

сферический колпачок SA = 2πRh
база SA = πr ²
Полная твердая сфера SA = 2πRh + πr ²
где R — радиус сферической крышки, r — радиус основания, а h — высота.

Дженнифер завидует земному шару, который ее старший брат Лоуренс получил на свой день рождения.Поскольку Дженнифер на две трети старше своего брата, она решает, что заслуживает одну треть земного шара своего брата. Вернув ручную пилу своего отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с R 0,80 фута и h 0,53 фута, как показано ниже:

SA = 2π × 0,80 × 0,53 = 2,664 фута ²

Коническая Frustum

Площадь поверхности твердого прямоугольного усеченного конуса равна сумме площадей его двух круглых концов и площади его боковой поверхности:

круговой конец SA = π (R ² + r ² )
боковой SA = π (R + r) √ (R-r) ² + h ²
всего SA = π (R ² + r ² ) + π (R + r) √ (R-r) ² + h ²
где R и r — радиусы концов, h — высота

Пол делает вулкан в форме усеченного конуса для своего проекта научной ярмарки.Пол рассматривает извержения вулканов как явление насилия и, выступая против всех форм насилия, решает сделать свой вулкан в форме закрытой конической усеченной пирамиды, которая не извергается. Хотя его вулкан вряд ли произведет впечатление на судей научной ярмарки, Пол все равно должен определить площадь поверхности материала, который ему нужен для покрытия внешней стены своего вулкана с R 1 фут, r 0,3 фута и h 1,5 фута:

всего SA = π (1 ² + 0,3 ² ) + π (1 + 0.3) √ (1 — 0,3) ² + 1,5 ² = 10,185 футов ²

Эллипсоид

Для вычисления площади поверхности эллипсоида нет простой и точной формулы, такой как куб или другая более простая форма. В калькуляторе выше используется приблизительная формула, предполагающая, что эллипсоид почти сферический:

SA ≈ 4π ^1,6 √ (a ^1,6 b ^1,6 + a ^1,6 c ^1,6 + b ^1,6 c ^1,6 ) / 3
где a , b и c — оси эллипса

Колтен всегда любил готовить и недавно выиграл на конкурсе керамический нож.К несчастью для своей семьи, которая почти полностью ест мясо, Колтейн практиковал свою технику нарезки чрезмерного количества овощей. Вместо того, чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических разрезов кабачков с осями 0,1, 0,2 и 0,35 дюйма:

SA ≈ 4π ^1,6 √ (0,1 ^1,6 0,2 ^1,6 + 0,1 ^1,6 0,35 ^1,6 + 0,2 ^1,6 0,35 ^1.6 ) / 3 = 0,562 дюйма ²

Квадратная пирамида

Площадь поверхности квадратной пирамиды складывается из площади ее квадратного основания и площади каждой из четырех треугольных граней. Учитывая высоту h и длину кромки a , площадь поверхности можно рассчитать с помощью следующих уравнений:

база SA = ²
боковая SA = 2a√ (a / 2) ² + h ²
всего SA = a ² + 2a√ (a / 2) ² + h ²

В классе Вонквайлы недавно завершено строительство модели Великой пирамиды в Гизе.Тем не менее, она считает, что модель не излучает того архитектурного чуда, как оригинал, и решает, что покрытие ее «снегом», по крайней мере, придаст вид чуда. Она вычисляет площадь поверхности расплавленного сахара, которая потребуется ей, чтобы полностью покрыть пирамиду, с длиной ребра a 3 фута и высотой h 5 футов:

всего SA = 3 ² + 2 × 3√ (3/2) ² + 5 ² = 40,321 футов ²

В отличие от Великой пирамиды в Гизе, которая простояла тысячи лет, ее модель, сделанная из крекеров и покрытая сахаром, просуществовала всего несколько дней.

Единицы общего пользования

Единица	метр 2
километр 2	1,000,000
сантиметр 2	0,0001
миллиметр 2	2	микрометр	0,000000000001
га	10,000
миля 2	2,589,990
ярд 2	0.83613
фут 2	0,092903
дюйм 2	0,00064516
акров	4,046,86

SA: у кубов и квадратов те же свойства, что и у сфер?

Студенты-математики часто бывают заинтригованы, когда понимают, что производная формулы объема сферы по радиусу сферы является формулой поверхности сферы:.Они также очарованы тем фактом, что производная от формулы площади круга является формулой для его длины:. Эти результаты, кажется, неприменимы к кубам и квадратам, потому что площадь поверхности куба и периметр квадрата. Почему сферы и круги ведут себя так, а кубы и квадраты — по-другому?

Рассмотрим производную площади круга. Согласно определению производной:

Геометрически этот результат легко увидеть, потому что область между двумя концентрическими окружностями, одна с радиусом r , а другая с радиусом r + h , по существу представляет собой полосу шириной h и длиной 2π r , как показано на рисунке 1.

Аналогичное вычисление справедливо для производной объема сферы. Согласно определению производной:

Геометрически этот результат легко понять, поскольку область между двумя концентрическими сферами, одна с радиусом r, а другая с радиусом r + h , по существу представляет собой полый шар толщиной h и площадью поверхности 4π r ² .

Подобные результаты не верны для стандартной формулы для объема куба и площади квадрата, как показано в первом абзаце.Давайте рассмотрим различные формулы: Пусть s будет расстоянием от центра квадрата перпендикулярно противоположной стороне, как показано на рисунке 2. Тогда, поскольку s составляет половину длины края квадрата, мы имеем формула A = (2 s ) ² = 4 s ² и P = 8 s , для площади квадрата и периметра квадрата соответственно.

Рассмотрим производные этой новой формулы площади квадрата.Так как A = 4 s ² , что является нашей формулой для периметра квадрата. Аналогично, пусть s будет расстоянием от центра куба перпендикулярно противоположной стороне. Тогда, поскольку s составляет половину длины ребра куба, мы имеем формулу V = (2 s ) ³ = 8 s ³ для объема куба, и (2 с ) ² = 4 с ² для площади каждой грани.Поскольку V = 8 s ³ , то, что в 6 раз превышает площадь грани куба, и, таким образом, это выражение равно площади поверхности куба. Записав формулы в терминах s , половина длины ребра, мы теперь имеем формулы, которые имеют свойства, согласующиеся со свойствами сфер и кругов.

Мы можем распространить этот результат на равносторонние треугольники. Пусть e будет длиной ребра треугольника, как показано на рисунке 3.

Площадь треугольника равна, а его периметр равен 3 e . Производная площади равна, что отдаленно не похоже на периметр треугольника. Давайте теперь изменим переменную, и пусть s представляет собой перпендикулярное расстояние от центра треугольника до одной из сторон, как показано на рисунке 4.

Используя соотношение Пифагора, или. В терминах s , площадь треугольника равна, а периметр равен. Поскольку производная площади равностороннего треугольника равна периметру треугольника.Рисунок 5 показывает, что разница между треугольными областями с использованием s и s + h , по сути, представляет собой трехстороннюю полосу шириной h и длиной, равной периметру треугольника, что геометрически подтверждает наш результат.

Случай равностороннего треугольника предлагает способ обобщения этого результата на другие правильные многоугольники. Отрезок s от центра многоугольника перпендикулярно стороне называется апофемой многоугольника.Тогда длина стороны многоугольника равна, где n — количество сторон, и, следовательно, периметр многоугольника равен. Площадь многоугольника — это длина апофемы, умноженная на половину длины периметра. В символах:

Теперь мы можем проверить это, периметр правильного многоугольника.

Предложите своим ученикам применить этот метод к правильному шестиугольнику. Они должны найти формулы для площади и периметра шестиугольника с точки зрения его апофемы.Затем они должны показать, что одно является производным от другого.

Мы также можем распространить наши результаты на трехмерные фигуры. Для правильных многогранников апофема — это радиус вписанной сферы. Рассмотрим тетраэдр.

Стандартные формулы для объема и площади поверхности тетраэдра обычно основаны на длине ребра, a , тетраэдра. Однако нетрудно переписать их в терминах длины r апофемы — радиуса вписанной сферы.

r = радиус вписанной сферы = апофема многогранника
R = радиус описанной сферы
a = длина края тетраэдра
S = площадь поверхности тетраэдра
V = объем тетраэдра

В пересчете на r вписанный радиус:

Таким образом, мы легко можем видеть, что в терминах апофемы производной формулы для объема тетраэдра является формула для его площади поверхности.

Аналогично, используя стандартные формулы для объема и площади поверхности октаэдра на основе длины ребра, a , октаэдра. Мы можем переписать их в терминах длины апофемы х .

Опять же, ясно, что производная формулы объема по отношению к r является формулой для площади поверхности.

Вот формулы для объема и площади поверхности двух других правильных многогранников через длину вписанного радиуса, r .

Додекаэдр:

Икосаэдр:

Вы можете предложить студентам сложную задачу проверки того, что производная приведенной выше формулы для объема додекаэдра на самом деле является данной формулой для его площади поверхности.

Какова ценность этого результата? Это просто академическое упражнение? Фактически, эти формулы предоставляют простой способ найти формулу для площади поверхности обычных твердых тел, если вы знаете формулу для их объема, или наоборот.Просто напишите формулу в терминах апофемы твердого тела и дифференцируйте или антидифференцируйте соответственно, чтобы найти другую формулу.

Ссылки

http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html#octahedron

http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html

Джон Ф. Махони представил AP Statistics в средней школе Banneker в 2002–2003 годах и обучил 59 студентов в этом году по этому курсу. Каждый из студентов сдал экзамен AP, и Махони считает, что у них, возможно, был самый высокий процент пожилых людей, сдающих статистику AP в стране.В этом году он также преподает исчисление AP уровня AB и BC. Он является консультантом по программе AP и давним участником программы AP Calculus Reading. В настоящее время он является одним из руководителей экзаменов. Он также возглавляет редакционную коллегию журнала NCTM ON-Math: www.nctm.org/onmath. В средней школе Баннекера он является одним из наставников команды робототехники и помогает студентам проектировать приводные механизмы на базе зубчатых колес — так же, как сам Баннекер делал более 200 лет назад. Им помогают многие инженеры, в том числе из Университета Говарда, расположенного через проспект Джорджии от средней школы.Он является одним из тренеров отмеченной наградами школьной команды It’s Academic. Когда он решил преподавать в средней школе Баннекера три года назад, после долгой карьеры в частных школах, он изучил математику Баннекера, и эта статья является результатом этой работы.

Калькулятор объема — прямоугольники, кубики

Вычислить объем прямоугольника или квадрата, плюс площадь его поверхности и количество жидкости, которое он может удерживать.

Калькулятор объема прямоугольника

…

Кубики квадратные, поэтому вам нужно ввести только одно измерение, так как все стороны равны. Введите высоту только для кубиков; Остальные размеры для кубов игнорируются. Для прямоугольников входить:

Высота сверху вниз; Ширина — расстояние слева направо; Глубина — измерение спереди назад.

Расчет площади прямоугольной поверхности

Площадь поверхности рассчитывается путем сложения всех внешних сторон прямоугольника или куба.

У прямоугольника шесть сторон: 3 набора по 2 стороны друг от друга одинакового размера. Чтобы вычислить площадь прямоугольника:

Верхняя / нижняя область (S1): 2 x ширина x глубина

Передняя / задняя боковая область (S2): 2 x ширина x высота

Левая / правая область (S3): 2 x глубина x высота

Площадь = S1 + S2 + S3

У куба все 6 сторон имеют одинаковый размер, поэтому расчет выглядит следующим образом:

Площадь = 6 * высота ²

Обратите внимание, что мы использовали высоту для куба, но можно использовать любую сторону.

Расчет объема прямоугольника

Объем — это то, сколько жидкости (или твердого вещества) может вместить прямоугольный кусок. Например, в аквариуме это количество галлонов воды в резервуаре. В прямоугольной глиняной запеканке это количество грязи, которую он мог удержать. Чтобы рассчитать объем прямоугольника:

Объем = высота * ширина * глубина

Результат вычисления объема прямоугольника выражается в кубических дюймах (или сантиметрах).С использованием объем, емкость прямоугольника по жидкости рассчитывается в нескольких общих показателях (чашки, унции, пинты, литров и т. д.)

Обратите внимание, что объем будет немного больше, чем требуется, если вы не измеряете его изнутри. стенки контейнера; В противном случае в расчет включается ширина стены со всех сторон.

Подробная информация о деривациях и примере

Объем куба: Объем куба — одна из важных и фундаментальных концепций, которая находит свое применение в различных сценариях.В общем, объем — это мера в кубических единицах, занимаемая твердой трехмерной фигурой. Мы знаем, что все стороны куба равны, а объем куба определяется произведением длины, ширины и высоты куба. В этой статье мы предоставили определение, вывод, формулу, решенные примеры и другие факты об объеме куба. Читай дальше что бы узнать!

Также проверьте:

Объем куба

Определение: Объем куба определяется как количество кубических единиц, занимаемых кубом.Математическое выражение для объема куба дается произведением длины трех сторон куба.

Что такое куб?

Куб — это трехмерная сплошная фигура с шестью равными квадратными гранями. Куб имеет восемь вершин и двенадцать сторон или ребер равной длины.

Каковы размеры куба?

У куба есть три основных размера:

• — Длина (L): Обычно под длиной понимается длина переднего края основания куба.
• — Ширина (B): Ширина — это длина стороны, перпендикулярной длине и в той же плоскости, что и основание.
• — Высота (H) или Глубина: Высота — это длина стороны куба, перпендикулярной основанию.

Формула объема куба

Объем куба можно определить, зная длину его ребер. Поскольку все ребра имеют одинаковую длину, длины любого ребра будет достаточно, чтобы вычислить объем куба.

Пусть ‘V’ будет объемом куба, а ‘a’ будет длиной ребер куба. Тогда объем будет равен:

Объем куба = длина × ширина × высота
V = a x a x a
V = a ³

Расчет объема куба

Давайте рассмотрим один из процессов, с помощью которого мы можем определить объем куба.

• — Давайте начнем с квадратной поверхности со сторонами, равными «а». Скажем, это квадратный лист бумаги, и первым делом нужно найти область.
• — Площадь бумаги определяется произведением ее длины и ширины. Следовательно, площадь квадрата будет ² ».
• — Теперь куб может быть сформирован путем наложения нескольких листов один на другой до тех пор, пока высота не станет равной единицам« а ».
• — Таким образом, площадь куба можно получить, вычислив произведение площади квадрата на высоту.
• Итак, объем куба будет равен ² x a.

Объем куба = a ² x a = a ³

Объем куба по диагонали

Допустим, длина диагонали дана, и нам нужно получить объем куба.В этом случае объем куба можно рассчитать по следующей формуле:

Объем куба = √3 × (d ³ /9)

Где
d — длина диагонали куба.

Площадь поверхности куба

У куба всего 6 равных квадратных поверхностей, и сумма площадей всех шести граней даст нам площадь поверхности куба. Пусть ‘a’ будет длиной стороны куба, которая также является длиной каждой квадратной поверхности. Тогда площадь куба будет равна:

Площадь поверхности куба = 6a ²

Решенные примеры для объема куба

Давайте рассмотрим некоторые из решенных примеров объема куба снизу:

Вопрос 01: Найдите объем куба со сторонами длиной 6 см.
Решение: Длина стороны куба 6 см.
Мы знаем, Объем куба = (длина сторон куба) ³
Таким образом, Объем = 6 ³
V = 216 см ³
Объем куба, имеющего длину стороны 6 см составляет 216 куб.

Вопрос 02: Найдите длину ребер куба, если его объем равен 343 см ³
Решение: Объем куба равен 343 см ³ .
Используя формулу объема куба, V = a ³
Следовательно, a = ³ √ 343
a = 7 см.
Следовательно, длина куба 7 см.

Бесплатные ресурсы для онлайн-исследований Embibe

Embibe предоставляет бесплатные учебные материалы для учащихся с 8 по 12 классы по таким предметам, как физика, химия, биология и математика. Студенты могут получить бесплатный доступ к этим материалам и подготовиться к экзаменам.

Часто задаваемые вопросы

Проверьте часто задаваемые вопросы ниже:

Q.Как получить объем куба? A. Объем куба можно рассчитать, найдя произведение длины, ширины и высоты куба.

В. Какова формула куба? A. Формула для вычисления объема куба: V = a 3

В. Каков объем 1 кубической единицы? A. Объем единичного куба равен 1 кубической единице.Куб длиной, шириной и высотой 1 единица превратится в объем 1 кубическую единицу.

В. Каковы отношения между объемом куба и длиной его ребра? A. Объем куба и длина ребра напрямую связаны. Объем «V» прямо пропорционален длине стороны «а». Это означает, что с изменением длины стороны будет меняться и объем.

Q.Сколько ребер в кубе? A. В кубе всего 12 ребер.

В. Могу ли я рассчитать объем куба, если задана длина диагонали? A. Да, вы можете рассчитать объем по приведенной ниже формуле: Объем куба = √3 × (d 3 /9)

Мы надеемся, что эта статья вам поможет. Если у вас есть какие-либо вопросы, не стесняйтесь размещать их в разделе комментариев ниже.Мы свяжемся с вами в ближайшее время.

630 Просмотры

Узнайте об объеме и площади поверхности

Из этого видео вы узнаете, как рассчитать объем и площадь поверхности выбранных твердых фигур, таких как призма, сфера, конус, цилиндр и пирамида.

Объем трехмерной фигуры — это объем занимаемого пространства.
Боковая область трехмерной фигуры представляет собой сумму самых внешних слоев фигуры, за исключением оснований.
Площадь поверхности трехмерной фигуры представляет собой сумму самых внешних слоев фигуры.

Призма
Объем:
Боковая площадь:
Площадь поверхности:

Пирамида
Объем:
Боковая площадь:
Площадь поверхности:

Цилиндр
Объем:
Боковая площадь:
Площадь поверхности:

Правый круговой конус
Объем:
Боковая площадь:
Площадь поверхности:

Сфера
Объем:
Боковая площадь:
Площадь поверхности:

Стенограмма видеоурока

В этом уроке мы рассмотрим формулы для вычисления объема и площади поверхности.

У нас есть сплошная фигура, формула для объема и формула для площади поверхности или площади

Начнем с призмы.

Например, призма может быть прямоугольной. Где верх и низ одинаковы и вытянуты по вертикали. Нижняя часть представляет собой прямоугольник, а верхняя часть также является прямоугольником. Куб — это тоже призма. У нас есть квадрат со всех шести сторон. У нас также может быть треугольная призма. Верх и низ представляют собой треугольник, а вертикальные линии вытянуты вверх.

Объем

где площадь основания, нам просто нужно узнать, какова площадь основания, а затем умножить ее на высоту.

Для куба мы должны узнать, какова площадь основного квадрата, умноженная на его высоту.

И для этого треугольника мы должны найти площадь основного треугольника, умноженную на его высоту.

Это определение объема призмы.

Что такое боковая область?

Боковая площадь — это площадь сторон.

Область передней, задней, левой и правой сторон. Мы должны найти всю боковую область вокруг.

Чтобы найти боковую площадь вокруг него, вам просто нужно умножить высоту на периметр.

Надо выяснить периметр базы. Для этого нам просто нужно сложить длину, умноженную на ее высоту.

Нам нужно найти общую площадь поверхности, мы должны найти площадь верхней и нижней части и добавить ее к общей боковой площади.

Теперь давайте посмотрим на объем и площадь поверхности пирамиды.

Пирамида имеет квадратное основание и простирается до точки над ним. Выглядит это примерно так.

У нас есть квадратное или прямоугольное основание, а все стороны — треугольники.

Формула объема пирамиды

где — площадь основания, в данном случае основание — квадрат.

Итак, мы должны вычислить площадь квадрата, умножив ее на его высоту.

Высота от низа до наивысшей точки; если вы внутри, то она идет прямо вниз и будет под прямым углом к ​​основанию.

Для расчета боковой площади пирамиды:

P — периметр основания.

В данном случае это квадрат. Просто сложите все стороны, умножьте его на высоту, и вы получите боковую площадь.

Боковая площадь — это площадь сторон. Исключает площадь основания. Вот почему нам нужно найти площадь квадратного основания и добавить ее.

Теперь посмотрим на цилиндр.

Цилиндр имеет круглую верхнюю и нижнюю части, как у банки, и имеет высоту.

Объем

очень похож на призму.

Здесь основание — круг.

Мы должны найти площадь круга.

Наша формула теперь

Боковая зона

Вот формула длины окружности.

У нас есть расстояние от основания круга, умноженное на его высоту.

По сравнению с формулой призмы, где высота умножается на периметр, здесь высота умножается на длину окружности.

Боковое пространство — это область вокруг цилиндра.Но здесь нет верха и низа. Если бы нам нужно было найти общую площадь поверхности цилиндра, нам нужно было бы вычислить площадь верха и низа, а затем добавить их.

Итак, общая площадь поверхности в данном случае составляет

, включая верх и низ.

Общая боковая площадь просто огибает стороны.

Теперь пройдемся по правому круговому конусу.

Основание правильного кругового конуса — круг. Затем он поднимается до точки или до вершины.

Объем

, где — площадь основания, а — высота, рассчитанная от самого верха до низа.

Основание — круг, так что

Наша формула объема теперь

Теперь посмотрим на боковую часть.

Боковая площадь

где — длина стороны конуса.

Это правильный круговой конус, поэтому, если мы проведем высоту посередине и продлим радиус до этой точки, мы получим прямой угол.

Итак, у нас получился прямоугольный треугольник с высотой и радиусом.

Теперь, когда у нас есть прямоугольный треугольник, мы можем найти длину, если она не задана с помощью теоремы Пифагора.

Мы делаем.

Боковая область даст нам область вокруг конуса, но не будет включать нижнюю часть конуса.

Если нам нужна общая площадь поверхности, включая базовый круг, мы должны сделать боковую площадь плюс площадь базовой окружности.

Обсудим объем и площадь поверхности шара.

Сфера похожа на шар или мрамор. Это круглая трехмерная фигура.

Объем шара

, а площадь —

Радиус идет от центра к краю.

Можно подумать о площади поверхности, если вы делаете кожаный баскетбольный мяч. Вы можете использовать площадь поверхности, чтобы определить, сколько кожи вам понадобится для изготовления мяча. Какая площадь вам понадобится, чтобы сделать мяч.

Хорошая особенность ближневосточных любительских регионов заключается в том, что вам даются формулы.Вам не нужно запоминать каждую формулу из этого списка.

Они фактически дают вам формулу объема пирамиды, но не формулу поперечной площади.

Кроме того, они дают вам формулу для объема и поперечной площади цилиндра.

Они дают вам формулу для объема и боковой площади правильного кругового конуса.