Конденсатор | Класс робототехники
Электрический конденсатор (англ. capacitor) — это устройство, которое может накапливать электрический заряд и хранить его некоторое время. Конденсаторы можно найти практически в любом электронном устройстве. Они бывают разных типов и размеров.
На электрических схемах конденсаторы обозначают двумя параллельными черточками. При этом, у полярных конденсаторов около положительного электрода дополнительно ставится плюсик.
Для чего нужен конденсатор?
У этого прибора есть множество применений. Мы не будем перечислять их все, отметим лишь некоторые.
1) Фильтрация пульсаций в цепях питания. Конденсаторы часто ставят на входе и выходе преобразователей напряжения, на входе питания микросхем. В этом случае конденсаторы служат своего рода амортизаторами, которые могут сгладить неровности напряжения, подобно амортизаторам автомобиля, сглаживающим неровности дороги.
2) Времязадающие электрические цепи.
Конденсаторы разной ёмкости заряжаются и разряжаются за разное время. Эту особенность используют в устройствах, где необходимо отсчитывать определенные промежутки времени. Например, с помощью резистора и конденсатора задается период и скважность импульса в микросхеме таймера 555 (урок про таймер 555).
3) Датчики прикосновения. В роли одной из обкладок конденсатора может выступить человек. Эту особенность нашего тела используют в своей работе сенсорные кнопки, тачскрины и тачпады некоторых видов.
4) Хранение данных. Конденсаторы применяются для хранения данных в оперативной памяти — ОЗУ (SRAM). Каждый модуль такой памяти содержит миллиарды отдельных конденсаторов, которые могут быть заряжены или разряжены, что интерпретируется как единица или ноль.
И это далеко не все варианты применения этого незаменимого прибора. Попробуем разобраться, как устройство конденсатора позволяет ему выполнять столько полезных функций!
Устройство простейшего конденсатора
Конденсатор состоит их двух металлических пластин — электродов, называемых также обкладками, между которыми находится тонкий слой диэлектрика.
Собственно, все конденсаторы устроены именно таким (или почти таким) образом, разве что меняется материал обкладок и диэлектрика.
Чтобы увеличить ёмкость конденсатора, не увеличивая его размеры, применяют разные хитрости. Например, если мы возьмем две обкладки в виде длинных полосок фольги, проложим между ними хотя бы тот же полиэтилен и свернем все это как рулет, то получится очень компактный прибор с большой ёмкостью. Именно так устроены плёночные конденсаторы.
Если вместо полиэтилена взять бумагу и пропитать её электролитом, то на поверхности фольги образуется тонкий слой оксида, который не проводит ток. Такой конденсатор будет называться электролитическим.
Существует много разных видов конденсаторов: бумажные, плёночные, оксидные алюминиевые и танталовые, вакуумные и т.п. В нашем уроке мы будем использовать оксидные электролитические конденсаторы из-за их большой ёмкости и доступности.
Полярные и неполярные конденсаторы
Очень важным является разделение конденсаторов на полярные и неполярные.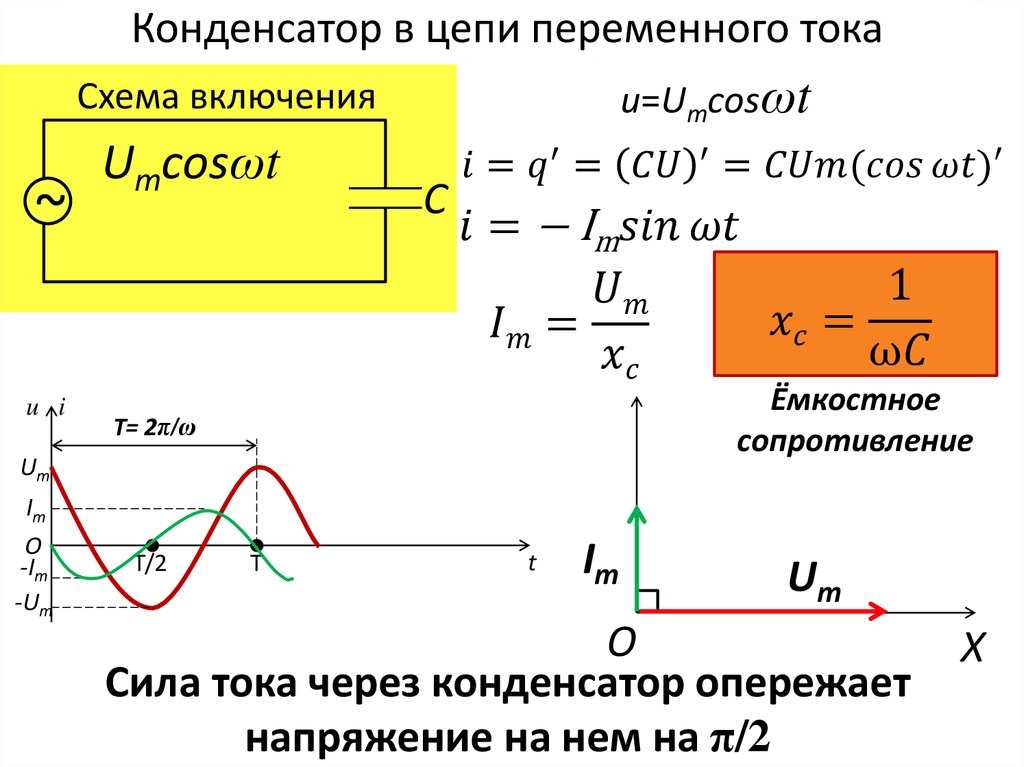
Приборы на основе оксидов: электролитические алюминиевые и танталовые обычно являются полярными, а значит если перепутать их полярность — они выйдут из строя. Причём этот выход из строя будет сопровождаться бурной электрохимической реакций вплоть до взрыва конденсатора.
На полярных конденсаторах всегда имеется маркировка. Как правило на электролитических конденсаторах на корпусе контрастной полосой отмечается отрицательный вывод (катод), у танталовых (в желтых прямоугольных корпусах) полоской помечается положительный вывод (анод). Если есть сомнения в маркировке, то лучше найти документацию на этот конденсатор и убедиться.
Неполярные же конденсаторы можно включать в цепь какой угодно стороной. К примеру, многослойные керамические конденсаторы — неполярные.
Ёмкость и напряжение конденсатора
Теперь обратим внимание на две важные характеристики конденсатора: ёмкость и номинальное напряжение.
Ёмкость конденсатора характеризует способность конденсатора накапливать заряд.
Это как ёмкость банки, в которой хранится, к примеру, вода. Кстати, не зря одним из первых электрических конденсаторов была так называемая Лейденская банка. Она представляла собой обыкновенную стеклянную посуду, снаружи обмотанную фольгой. В банку была налита токопроводящая жидкость — электролит. Фольга и электролит играли роль обкладок, а стекло банки служило тем самым диэлектрическим барьером.
Ёмкость электрического конденсатора измеряют в фарадах. В схемах ёмкость обозначают латинской буквой C. Как правило, ёмкость классических конденсаторов варьируется от нескольких пикофарад (пФ) до нескольких тысяч микрофарад (мкФ). Ёмкость указывается на корпусе конденсатора. Если единицы не указаны — то это пикофарады. Микрофарады часто обозначают как uF — так как буква u внешне похожа на греческую букву мю, которую используют вместо приставки микро.
Существует и особый вид конденсаторов, называемых ионисторами (англ. supercapacitor), которые имеют ёмкость в несколько фарад! Чем больше ёмкость конденсатора, тем больше энергии в нём может храниться и тем дольше он заряжается, при прочих равных условиях.
Номинальное напряжение — второй важный параметр. Это такое напряжение, при котором конденсатор будет работать весь срок службы без критичного изменения своих параметров. Нельзя применять в 12-вольтовой цепи конденсатор на 6 вольт — он быстро выйдет из строя.
Именно эти два параметра обычно наносят на поверхность корпуса конденсатора. На фотографии ниже изображён электролитический конденсатор ёмкостью 470 мкФ и номинальным напряжением 16 Вольт.
А вот на керамических конденсаторах часто указывают только ёмкость. На картинке ниже конденсатор имеет маркировку 104. Что бы это значило?
Последняя цифра в этом коде — количество нулей после двухзначного числа в начале. 104 = 10 0000 пФ = 100 нФ = 0,1 мкФ
Параллельное и последовательное подключение конденсаторов
Как и в случае резисторов, конденсаторы можно составлять в цепочки. Это бывает нужно, когда в схеме необходима какая-то конкретная ёмкость, а у вас нет такого конденсатора.
Параллельное подключение
В отличие от резисторов, при параллельном подключении конденсаторов их ёмкости складываются.
Например, если нам нужно получить ёмкость 3000 мкФ, а у нас есть два конденсатора по 1000 мкФ, и 10 штук по 100 мкФ, смело ставим их параллельно и получаем: 1000*2+100*10 = 2000 + 1000 = 3000 мкФ
Последовательно подключение
При последовательном подключении конденсаторы ведут себя как резисторы, соединённые параллельно. Например, посчитаем суммарную ёмкость двух конденсаторов на 100 мкФ, соединённых последовательно:
Суммарная ёмкость Ctot = 50 мкФ.
Заряд и разряд конденсатора — RC-цепочка
Теперь разберёмся с процессами, происходящими внутри конденсатора во время заряда и разряда. Для этого рассмотрим самую простую электрическую цепь с конденсатором. С левой стороны схемы подключим источник питания. Сверху разместим ключ и резистор, а справа сам конденсатор. Участок цепи, на котором есть конденсатор и резистор называют RC-цепью.
При замыкании ключа, в такой цепи образуется электрический ток, сила которого зависит от сопротивления резистора и внутреннего сопротивления самого конденсатора.
Заряженные частицы устремятся к конденсатору, но не смогут преодолеть слой диэлектрика (по крайней мере все разом). Вследствие чего, с одной стороны конденсатора накопятся отрицательно заряженные частицы, а с другой стороны — положительно заряженные. Концентрация заряженных частиц на обкладках создаст мощное электрическое поле между ними.
С течением времени, напряжение на конденсаторе растет, а сила тока падает. После завершения процесса заряда, ток в цепи упадет почти до нуля. Останется только очень маленький ток утечки, который образуется благодаря тому, что некоторым заряженным частицам всё же удается проскочить через слой диэлектрика. Напряжение, напротив, станет практически равным напряжению источника.
Когда мы отключим конденсатор от источника питания, этот самый ток утечки постепенно разрядит конденсатор. Эта особенность электрических конденсаторов не даёт нам сделать из них контейнер для длительного хранения энергии. Хотя частично эту проблему решают ионисторы.
Резистор и время заряда конденсатора
Зачем в цепи нужен резистор? Что на мешает подключить его напрямую к источнику? Тому есть две причины.
Резистор ограничивает ток, протекающий через конденсатор. Чем меньше заряженных частиц за единицу времени прибывает в конденсатор, тем больше времени для заряда ему потребуется.
Конденсатор заряжается и разряжается по экспоненциальному закону. Зная это, мы можем легко рассчитать время заряда/разряда в зависимости от его ёмкости и от сопротивления резистора.
По картинке можно понять, что за время T конденсатор заряжается на 63,2%. А вот за время 3T уже на 95%. Время T здесь равно произведению ёмкости конденсатора C на сопротивление R, последовательно соединенного резистора:
Например, у нас есть конденсатор ёмкостью 100 мкФ, соединенный с резистором 1 кОм. Посчитаем за сколько секунд он зарядится хотя бы до 95%:
Теперь умножаем это на 3 и получаем 3T = 0,3 секунды — за такое время конденсатор почти полностью будет заряжен.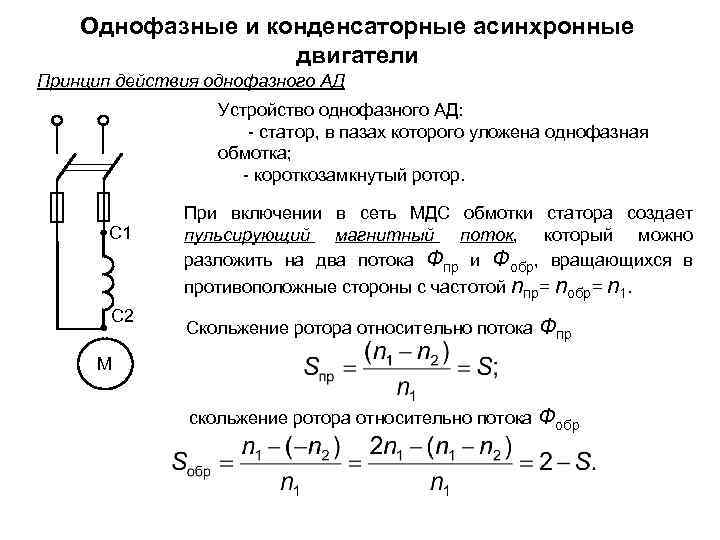
Таким образом, меняя ёмкость конденсатора и резистора мы можем управлять временем его заряда, что нам ещё пригодится в будущем.
Вторая важная причина, по которой в цепи присутствует резистор — защита источника питания. Дело в том, что разряженные конденсаторы имеют очень низкое внутреннее сопротивление, которое составляет доли Ома. По сути, их можно рассматривать как обычные проводники. А что будет, если замкнуть выводы питания проводником? Будет короткое замыкание! Такой режим работы цепи является аварийным для источника питания, и его нужно всячески избегать.
Плавное выключение светодиода при помощи конденсатора
Проведем небольшой опыт. Для этого соберем на макетной плате цепь с кнопкой, конденсатором и светодиодом. В качестве источника питания используем контакты питания Ардуино Уно.
Принципиальная схема
Внешний вид макета
Подключим Ардуино к питанию. Затем, нажмем кнопку и светодиод практически мгновенно загорится.
Отпустим кнопку — светодиод медленно начнет гаснуть. Почему так происходит?
Сразу после подключения нашей схемы к источнику питания, в ней начинают происходит интересные процессы.
Как уже говорилось ранее, пока конденсатор пустой, ток через него максимален. Следовательно, конденсатор начинает стремительно набирать заряд. При этом светодиоду, который подключен параллельно, ничего не достается 🙁 Напряжение на нем близко к нулю.
С течением времени конденсатор насыщается, благодаря чему ток начинает постепенно переходить в параллельную цепь — через светодиод. Напряжение на светодиоде начинает расти. Наступает момент, когда напряжение на светодиоде принимает критическое значение (для красного светодиода около 1,8 В), при котором он стремительно отбирает остатки тока у конденсатора и вспыхивает!
Когда мы отпускаем кнопку, ситуация становится гораздо проще. Конденсатор становится источником питания для светодиода с резистором. Светодиод начинает медленно высасывать заряд из конденсатора, пока тот не разрядится.
Тут мы и наблюдаем медленно угасание.
Меняя сопротивление R1, мы можем влиять на скорость вспыхивания светодиода. Однако, следует учитывать, что увеличивая R1 мы будем снижать ток в цепи, тем самым уменьшая максимальный заряд конденсатора и яркость светодиода.
Увеличивая C1, мы получим более длительное время работы светодиода после выключения источника. Это как поставить более ёмкую батарейку.
Наконец, меняя R2 можно регулировать яркость светодиода, и соответственно, время его работы. Ведь чем меньше тока мы забираем из конденсатора, тем на большее время его хватит.
К размышлению
Итак, мы познакомились с конденсатором — интересным и порой опасным жителем любой электронной платы. В следующих уроках уделим внимание резистору и индуктивности, а также более сложному их собрату — транзистору.
Как рассчитать емкость гасящего конденсатора простого блока питания. . Обзоры товаров из Китая.
Блок питания с гасящим конденсатором представляет собой простейший вариант запитать какое нибудь маломощное устройство.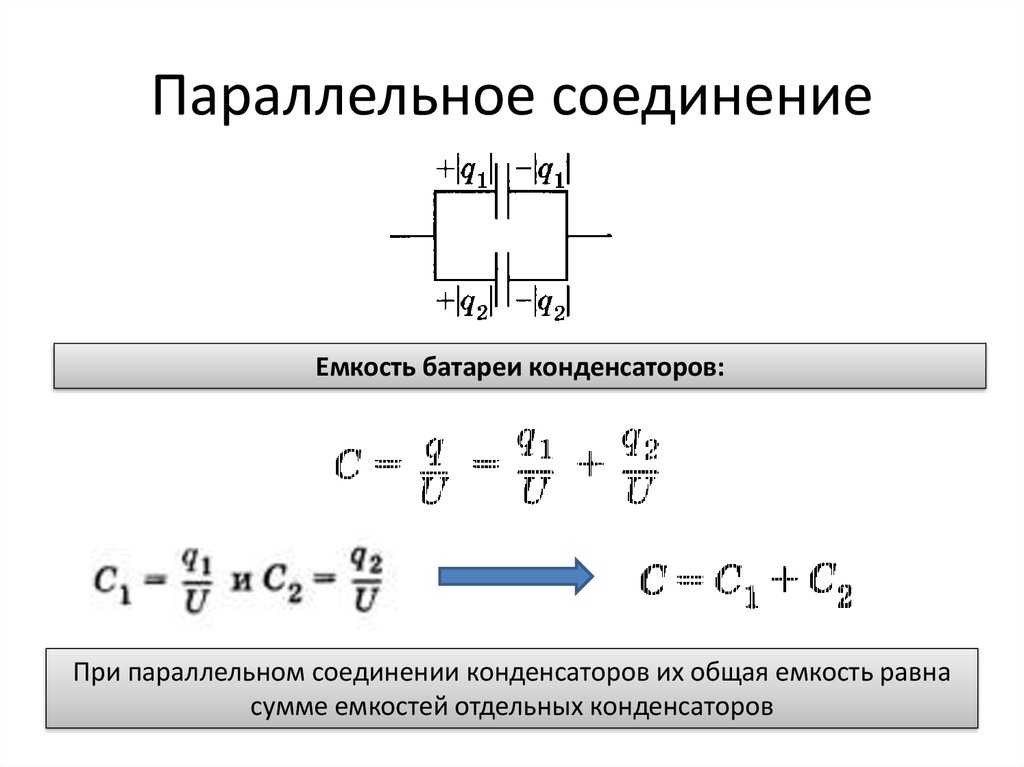
При всей своей простоте он имеет и два минуса:
1. Он гальванически связан с сетью! потому такие БП используются там, где нет вероятности прикосновения к контактам.
2. Такой Бп имеет не очень большой выходной ток. При увеличении выходного тока надо увеличивать емкость гасящего конденсатора и его габариты становятся существенными.
Внимание, будьте очень аккуратны, не прикасайтесь к контактам этого БП когда он включен.
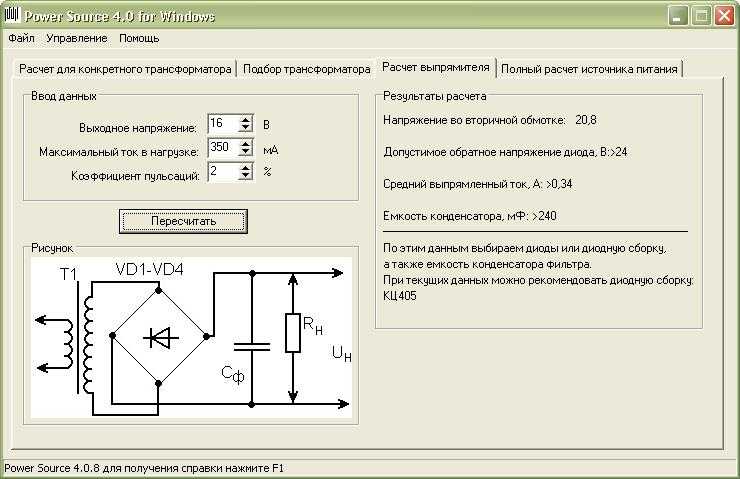
Простейшая схема данного БП выглядит так:
Как можно увидеть из схемы, последовательно с сетью стоит конденсатор. Он то и является балластом,, на котором гасится часть напряжения.
Конденсатор не пропускает постоянный ток, но так как в сети переменный и конденсатор в итоге постоянно перезаряжется, то и получается, что в таком случае ток на выходе есть. Причем сила тока напрямую зависит от емкости конденсатора.
Собственно потому для расчета емкости конденсатора необходимо знать как минимум выходной ток нашего будущего БП, причем надо учесть и потребление стабилизатора, обычно это несколько мА.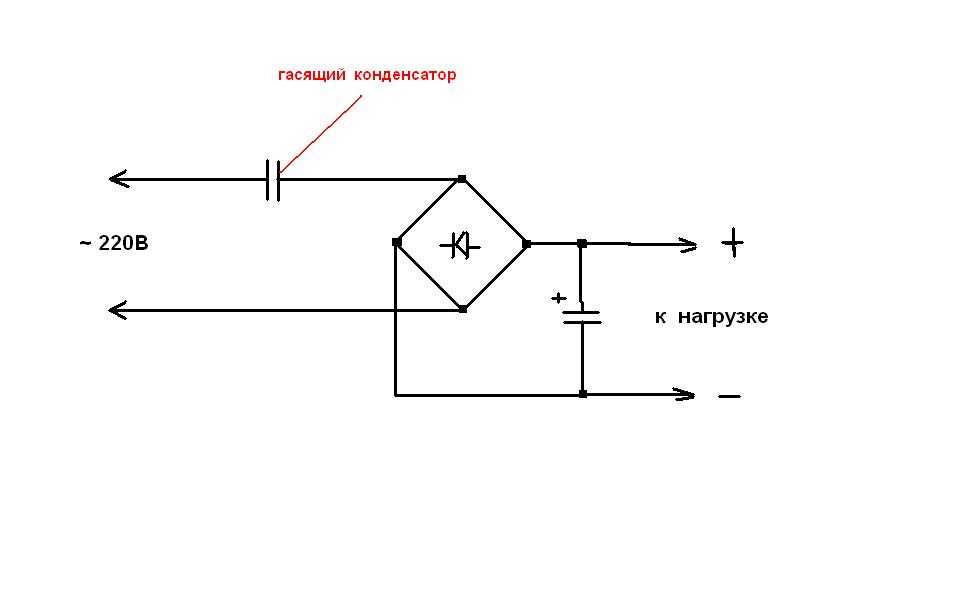
И так. Есть две формулы, сложная и простая.
Сложная — подходит для расчета при произвольном выходном напряжении.
Простая — подходит в ситуациях, когда выходное напряжение не более 10% от входного.
I — выходной ток нашего БП
Uвх — напряжение сети, например 220 Вольт
С — собственно искомая емкость.
Например я хочу сделать БП с выходным током до 150мА. Пример схемы приведен выше, вариант применения — радиопульт с питанием 5 Вольт + реле на 12 Вольт.
Подставляем наши 0.15 Ампера и получаем емкость 2.18мкФ, можно взять ближайший номинал из стандартных — 2,2мкФ, ну или «по импортному» — 225.
Все как бы вроде хорошо, схема простая, но есть несколько минусов, которые надо исключить:
1. Бросок тока при включении может сжечь диодный мост.
2. При выходе из строя конденсатора может быть КЗ
3. Если оставить как есть, то вполне можно получить разряд от входного конденсатора, так как на нем может долго присутствовать напряжение даже после отключения БП от сети.
4. При снятии нагрузки напряжение на конденсаторе до стабилизатора поднимется до довольно большого значения.
Решения:
1. Резистор R1 последовательно с конденсатором
2. Предохранитель 0.5 Ампера.
3. Резистор R2 параллельно конденсатору.
4. Супрессор на 12 Вольт параллельно конденсатору после диодного моста. Я не рекомендую здесь использовать стабилитроны, супрессоры рассчитаны на большую мощность рассеивания и схема будет работать надежнее.
На схеме красным цветом я выделил новые компоненты, синим — небольшое дополнение в виде светодиода.
Но гасящие конденсаторы используют часто и в дешевых светодиодных лампах. Это плохо, так как у таких ламп меньше надежность и часто высокие пульсации света.
Ниже упрощенный вариант схемы такой лампы.
Попробуем рассчитать емкость для такого применения, но так как напряжение на выходе будет явно больше чем 1/10 от входного, то применим первую формулу.
В качестве выходного напряжения я заложил 48 Вольт, 16 светодиодов по 3 Вольта на каждом.
Ток — 20мА, типичный максимальный ток для большинства индикаторных светодиодов.
У меня вышло, что необходим конденсатор емкостью 0.298 мкФ. Ближайший из распространенных номиналов — 0.27 или 0.33мкФ. Первый встречается гораздо реже, а второй уже будет давать превышение тока, потому можно составить конденсатор из двух параллельных, например по 0.15мкФ. При параллельном включении емкость складывается.
С емкостью разобрались, осталось еще пара моментов:
1. Напряжение конденсатора
2. Тип конденсатора.
С напряжением все просто, можно применить конденсатор на 400 Вольт, но надежнее на 630, хоть они и имеют больше размер.
С типом чуть сложнее. Для такого применения лучше использовать конденсаторы, которые изначально предназначены для такого использования, например К73-17, CL21, X2
А это более надежный вариант, не смотрите что на нем указано 280 Вольт, у него это значение переменного действующего напряжения и он будет работать надежнее, чем К73-17 или CL21.
Такие конденсаторы могут выглядеть и так
А вот теперь можно еще раз внимательно посмотреть, что надо для того, чтобы собрать такой «простой» блок питания и решить, нужен ли он.
В некоторых ситуациях да, он поможет, но он имеет кучу минусов, потому на мой взгляд лучше применить просто небольшой импульсный блок питания, который уже имеет стабилизированное выходное напряжение, гальваническую изоляцию и больший выходной ток.
Но можно поступить еще лучше. Сейчас получили распространение монолитные блоки питания. По сути кубик, в котором находится миниатюрный БП
Например HLK-PM01 производства Hi-link, стоимостью около двух долларов за штуку.
Или их китайский аналог TSP-05 производства Tenstar robot. Они немного дешевле, 1.93 доллара за штуку.
Практика показала, что качество у них сопоставимое.
Как я писал выше, они представляют из себя импульсный Бп в модульном исполнении.
БП в пластмассовом корпусе залитый эпоксидной смолой.
Выпускаются на разные напряжения и способны поддерживать его на довольно стабильном уровне.
Внутренности поближе, на фото вариант от Hi-link
На этом вроде все. Надеюсь, что статья была полезна, постараюсь и в будущем находить интересные темы. Также интересны пожелания, что хотелось бы видеть в рубрике — Начинающим.
Эту страницу нашли, когда искали:
расчет входного конденсатора безтрансформаторного бп, какие ставить конденсаторы в бп чтобы увеличить мощность, схема включения x2 конденсатора, как подобрать конденсатор для блока питания 36 вольт, расчет емкости конденсатора qx/Uвых, конденсатор гасящий калькулятор, сколько вольт вы найдете на основном конденсаторе прибора на 220 вольт, как рассчитать выходное напряжение через конденсатор, конденсатор 0.5 ампера, мощность электролитического конденсатора в бдоке питания, как погасить напряжение 40в с электролитического конденсатора до 25вольт, сглаживающий конденсатор на 19v 5a, какую ёмкость надо добавить,чтобы увеличить ток на 20 миллиампер, бaлaстный кондeнсaтор токоогрaничивaющий рeзистор, огрaничитeльный кондeнсaтор.
Основные расчеты конденсаторов — инженерное мышление
Конденсаторы используются во многих цепях для различных целей, поэтому мы изучим некоторые основные расчеты конденсаторов для цепей постоянного тока.
Прокрутите вниз, чтобы посмотреть обучающее видео на YouTube
Конденсаторы в цепях постоянного тока
Конденсаторы обычно выглядят так. У нас есть конденсатор электролитического и керамического типа.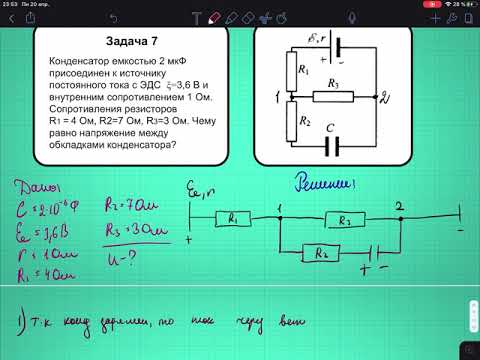
Электролитик поляризован, что означает, что одна сторона должна быть подключена к плюсу, а другая к минусу источника питания. Керамический тип, как правило, может быть подключен любым способом. На стороне электролитического конденсатора мы находим пунктирную линию, указывающую на отрицательную сторону, длинный вывод также указывает на положительную сторону нового конденсатора. Но они обычно обрезаются во время установки, поэтому не полагайтесь только на это. Эти два конденсатора представлены такими символами, обратите внимание, что поляризованный конденсатор имеет небольшой символ плюса, указывающий на положительную сторону.
При подключении к источнику постоянного тока напряжение батареи будет выталкивать электроны в конденсатор, поэтому конденсатор заряжается до того же напряжения, что и батарея. Конденсаторы заряжаются почти мгновенно при прямом подключении к батарее, но мы почти всегда используем резистор, это задержит время зарядки, и позже в этой статье мы увидим, как это рассчитать.
Внутри конденсатора с одной стороны скопилось много электронов, они не могут двигаться из-за изолирующего материала между двумя сторонами. Поскольку электроны заряжены отрицательно, у нас есть накопление заряда на одной стороне по сравнению с другой, поэтому у нас есть разница в напряжении между двумя выводами.
Эти электроны удерживаются на месте, и конденсатор может удерживать этот заряд в течение длительного периода времени. Когда указан путь, они будут разряжаться, пока не опустеют. Электроны не проходят через конденсатор; они просто накапливаются внутри, а затем высвобождаются.
Количество заряда, накопленного в конденсаторе, рассчитывается по формуле Заряд = емкость (в фарадах), умноженная на напряжение. Итак, для этого конденсатора 12 В 100 мкФ микрофарад мы конвертируем микрофарады в фарады (100/1 000 000 = 0,0001 Ф). Затем умножаем это на 12 В, чтобы увидеть, что он хранит заряд 0,0012 кулона. 92
= 0,5 x 0,0001F x 144
= 0,0072 Дж
Мы знаем, что конденсатор будет заряжаться до напряжения батареи.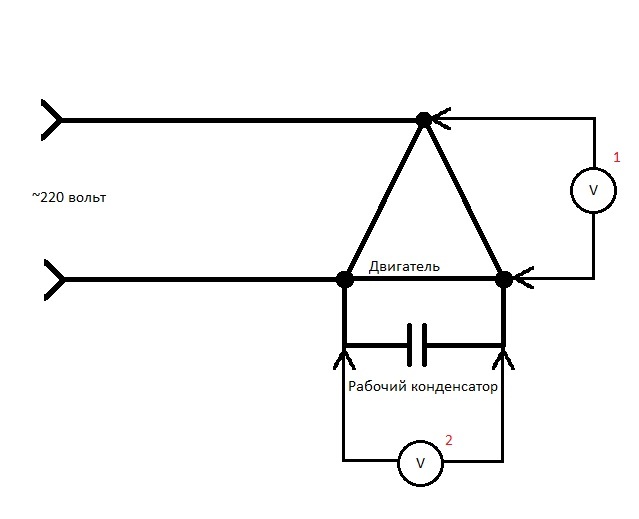
Итак, если мы подключим конденсатор таким образом, каково будет напряжение на конденсаторе? Будет 1,5В. Если мы вот так подключим конденсатор, каково будет его напряжение? Тоже будет 1,5В. Это два разных способа соединения конденсаторов в цепях, последовательное или параллельное. Это приведет к тому, что конденсаторы будут работать по-разному.
Параллельные конденсаторы
Если мы поставили конденсатор параллельно с лампой, то при извлечении батарейки конденсатор начнет питать лампу, она медленно тускнеет по мере разрядки конденсатора. Если бы мы использовали два конденсатора, мы могли бы питать лампу дольше.
Допустим, конденсатор 1 = 10 мкФ, а конденсатор 2 = 220 мкФ. Как рассчитать общую емкость? Это очень просто, ответ 230 мкФ. Конденсаторы соединены параллельно. Итак, 10 мкФ + 220 мкФ = 230 мкФ. Мы можем продолжать добавлять больше, например, конденсатор на 100 мкФ, и общее количество будет просто суммой всех конденсаторов. Размещая их параллельно, мы, по сути, объединяем их, чтобы сформировать больший конденсатор.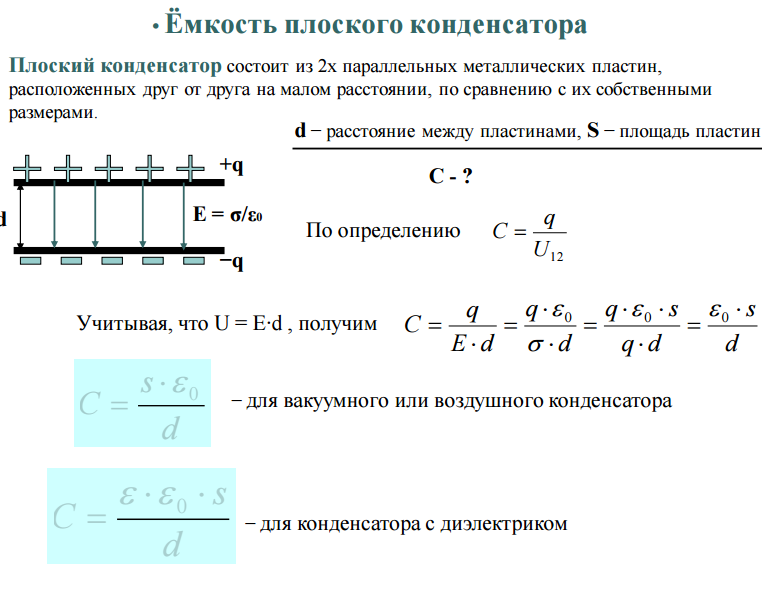
Это очень полезно, потому что, если, например, нам нужен большой конденсатор на 2000 мкФ, но у нас его нет, мы можем просто использовать конденсаторы меньшего размера, такие как 2x 1000 мкФ или 4x 500 мкФ и т. д. Он также часто используется для фильтрации шума и обеспечения большей емкости. ток в цепях с высоким потреблением.
Общий заряд, хранящийся в параллельных конденсаторах, равен: заряд = общая емкость, умноженная на напряжение. Итак, у нас есть батарея на 9 В и два конденсатора общей емкостью 230 мкФ. Поскольку это параллельно, этот провод 9 В, а этот 0 В, поэтому оба конденсатора заряжены до 9 В. Следовательно, 0,00023 Ф, умноженное на 9 В = 0,00207 кулона. И с тремя конденсаторами мы имеем 330 мкФ (0,00033 Ф), умноженные на 9 В = 0,00297 кулонов.
Мы также можем рассчитать заряд каждого конденсатора в отдельности. Мы просто используем одну и ту же формулу для каждого конденсатора, вы можете увидеть ответы на экране.
Конденсатор 1 = 0,00001 F x 9V = 0,00009 кулоны
Конденсатор 2 = 0,00022 F x 9V = 0,00198 кулоны
3 = 0,0001 F x 9V = 0,0009 Coulombs
= 0,00009 + 0,00198 + 0,0009 = 0,00297 Couls
. Если мы поместим конденсатор последовательно с лампой, когда мы нажмем переключатель, она загорится, но затем станет тусклее, когда конденсатор достигнет уровня напряжения батареи, и как только он достигнет этого, лампа погаснет. Помните, что электроны не могут проходить через конденсатор из-за изолирующего материала внутри. Электроны просто накапливаются внутри одной пластины и по мере их накопления отбрасывают такое же количество с противоположной пластины. Таким образом, ток может течь только тогда, когда конденсатор заряжается или разряжается. В настоящее время, когда батарея удалена, конденсатор не может разрядиться, поэтому он будет удерживать напряжение на том же уровне. Неважно, подключаем мы аккумулятор или отключаем, лампа не включится. Однако, если мы обеспечим другой путь, то при нажатии переключателя конденсатор теперь может разряжаться, так что электроны могут течь через лампу и освещать ее. Он станет тусклее по мере разрядки конденсатора.
Что, если бы у нас было 2 конденсатора, соединенных последовательно, опять же, конденсатор 1 имеет емкость 10 мкФ, а конденсатор 2 — 220 мкФ. Как найти полную емкость? Для этого мы используем эту формулу, она может показаться сложной, но на самом деле она очень проста. Все, что нам нужно сделать, это ввести значения наших конденсаторов 10 и 220 мкФ. Мы можем ввести это как это на наших калькуляторах или в Excel. Но при ручном вычислении мы делаем 1, деленное на 10, что равно 0,1, и 1, деленное на 220, что равно 0,00454. Мы складываем их вместе, чтобы получить 0,10454, а затем 1, деленное на это, дает в общей сложности 9.0,56 мкФ. Обратите внимание, что общая емкость теперь меньше конденсатора с наименьшим значением.
Если мы добавили в схему третий конденсатор на 100 мкФ, то получим общую емкость 8,73 мкФ. Значит, уменьшилось еще больше. Это потому, что, объединяя их последовательно, мы существенно увеличиваем толщину изоляционного материала, поэтому притяжение отрицательно заряженных электронов к положительно заряженным отверстиям на противоположной пластине становится слабее.
Общий заряд последовательных конденсаторов находится по формуле: заряд = емкость (в фарадах), умноженная на напряжение.
Итак, если мы использовали 9V батареи, мы переводим микрофарады в фарады и видим, что общий заряд равен 0,00008604 кулонов
(0,00000956F x 9V = 0,00008604 кулонов)
Кулоны)
Заряд, удерживаемый каждым конденсатором в отдельности, очень легко рассчитать в последовательных цепях. Это то же самое, что общее количество. Каждый конденсатор содержит одинаковое количество электронов при последовательном соединении. Это потому, что когда мы заряжали конденсаторы, ток был одинаковым во всех частях цепи. То же самое количество электронов, которые были вытолкнуты в одну пластину, были вытеснены из противоположной пластины, поэтому каждый последовательный конденсатор может быть заряжен только до одного и того же уровня. Таким образом, наименьший конденсатор будет ограничивающим фактором.
Однако, поскольку каждый конденсатор может иметь разную емкость, напряжение каждого конденсатора будет разным. Напряжение каждого конденсатора находим по формуле напряжение = заряд (в кулонах) деленное на емкость (в фарадах).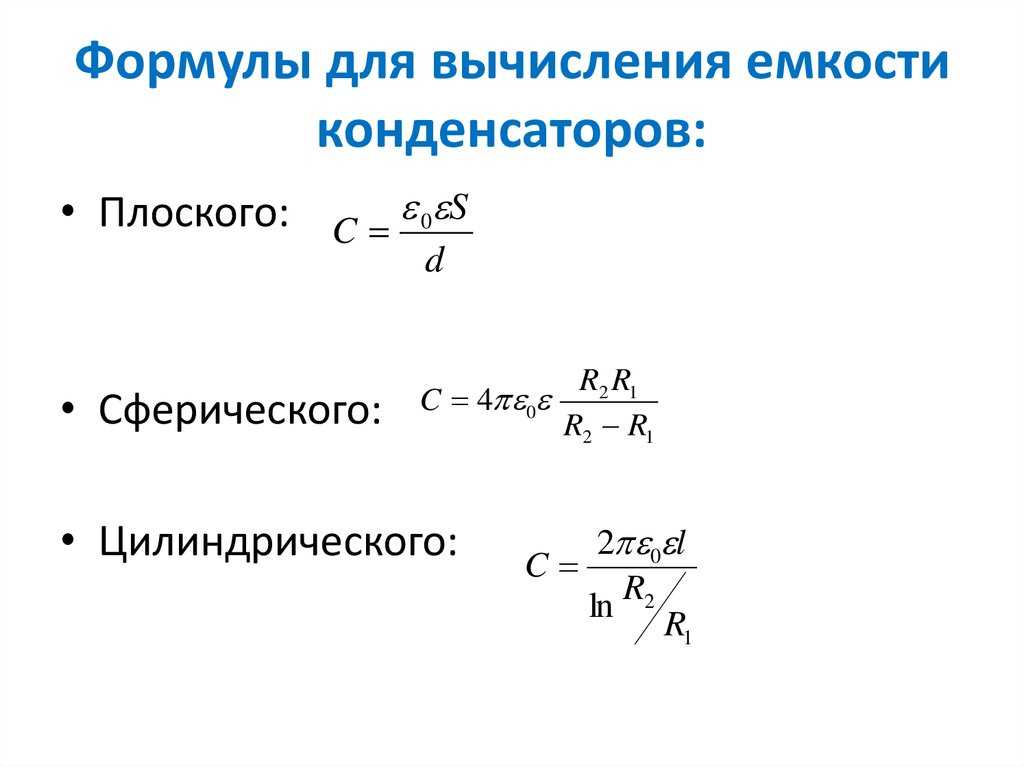
Итак, для этой схемы мы видим, что конденсатор 1 на 7,8 В, конденсатор 2 на 0,35 В и конденсатор 3 на 0,78 В. Они объединяются в общее напряжение батареи, которое составляет 9 В.
Конденсатор 1: 0,00007857 C / 0,00001 F = 7,857 В
Конденсатор 2: 0,00007857 C / 0,00022 F = 0,357 В
Конденсатор 3: 0,00007857 C / 0,0001 F = 0,786 В
Общее напряжение = 7,857 В + 0,357 В + 0,786 В = 9 В переключатель все последовательно. Конденсатор полностью разряжен, и мы считываем 0 В на двух выводах.
Когда мы замыкаем переключатель, конденсатор заряжается. Напряжение будет увеличиваться до тех пор, пока не сравняется с напряжением батареи. Рост напряжения не мгновенный, он имеет экспоненциальную кривую. Сначала напряжение быстро увеличивается, а затем замедляется, пока не достигнет того же уровня напряжения, что и батарея.
Мы разделили эту кривую на 6 сегментов, но нас интересуют только первые 5, потому что на 5 маркере мы в основном находимся на полном напряжении, поэтому мы можем игнорировать все, что дальше этого.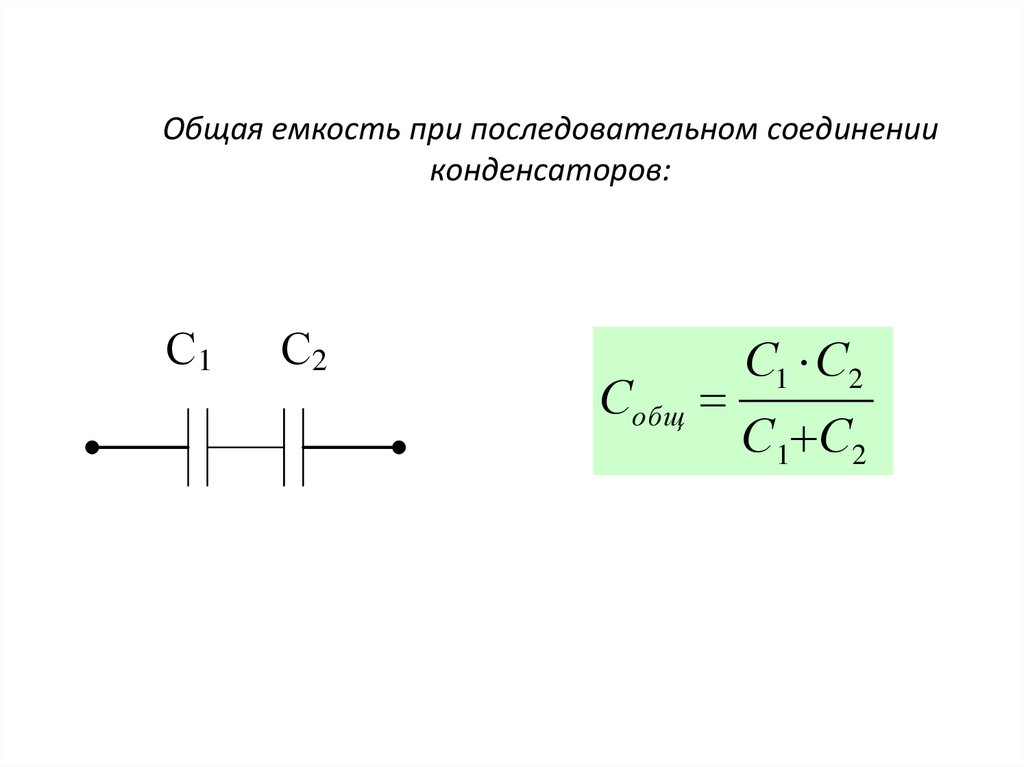
Каждый сегмент представляет нечто, называемое постоянной времени. Следовательно, поскольку у нас есть 5 сегментов, у нас есть 5 постоянных времени, поэтому потребуется 5 постоянных времени, чтобы зарядить конденсатор от 0 до чуть менее 100%. Все, что нам нужно сделать, это вычислить длину одной постоянной времени, а затем умножить ее на 5.
Чтобы вычислить одну постоянную времени, мы используем эту формулу.
Постоянная времени (в секундах) = сопротивление (в Омах), умноженное на емкость (в Фарадах). Итак, мы конвертируем резистор в омы, а емкость конденсатора в фарады и видим, что 10 000 Ом, умноженные на 0,0001 фарад, равняются 1. Итак, в этом примере постоянная времени равна 1 секунде. Следовательно, 5 из них — это 5 секунд. Это означает, что для полной зарядки этого конденсатора до 9 В требуется 5 секунд.
Если бы сопротивление резистора составляло всего 1000 Ом, постоянная времени была бы равна 0,1 секунды, поэтому для достижения
потребовалось бы 0,5 секунды.
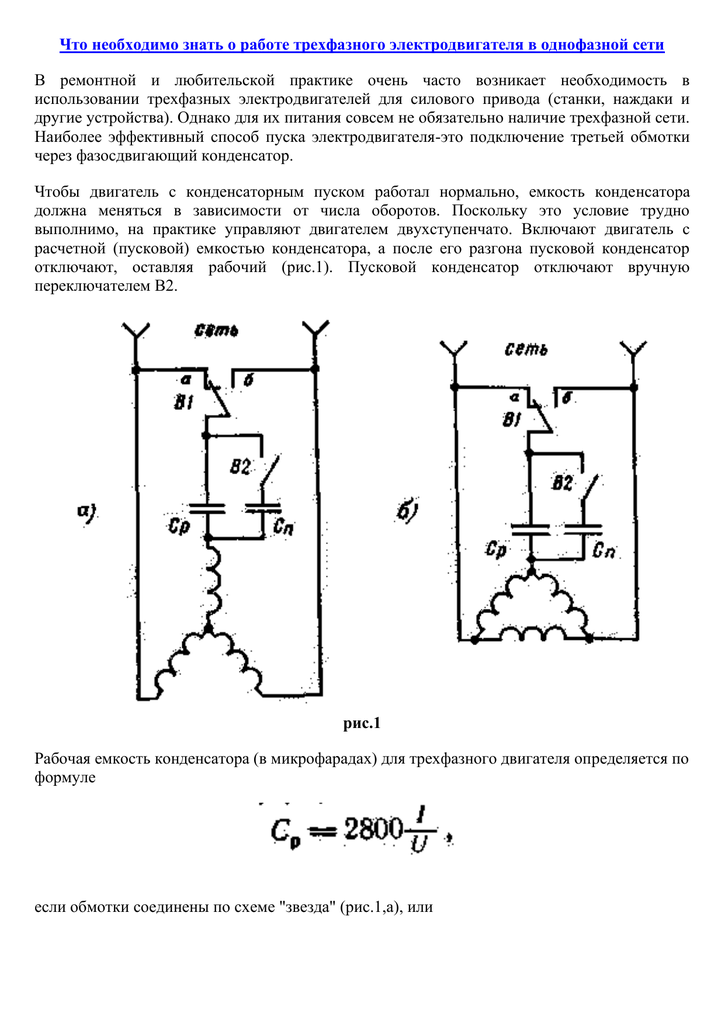V. Если бы конденсатор был 1000 микрофарад, это заняло бы всего 50 секунд. Таким образом, с увеличением размера конденсатора время, затрачиваемое на это, увеличивается. Если значение резистора увеличивается, время, необходимое для этого, также увеличивается.Возвращаемся к нашей исходной схеме. Таким образом, мы можем рассчитать уровень напряжения для каждой постоянной времени. В точке 1 напряжение всегда равно 63,2 %, в точке 2 — 86,5 %, в точке 3 — 95 %, в точке 4 — 98,2 % и в точке 5 — 99,3 %.
Итак, в этом примере через 1 секунду напряжение на конденсаторе составляет 5,68 В, через 2 секунды — 7,78 В, через 3 секунды — 8,55 В, через 4 секунды — 8,83 В и через 5 секунд — 8,9 В.4V
Если вам нужен более точный ответ, мы можем рассчитать каждую точку следующим образом.
Точка 1 = 9В-0В)x0,632 = 5,6880В
Точка 2 = ((9В – 5,688В)x0,632)+5,68В = 7,7812В
Точка 3 = ((9В-7,7812В)x0,632 )+7,7812В = 8,5515В
Точка 4 = ((9В-8,55В)x0,632)+8,5515В = 8,8349В
Точка 5 = ((9В-8,8349В)x0,632)+8,8349В = 8,9393В
Помните, что при последовательном соединении ток в цепи уменьшается, а напряжение на конденсаторе увеличивается.
При полном напряжении ток в цепи не течет. Если бы резистор был лампой, он мгновенно достиг бы полной яркости, когда переключатель был замкнут, но затем стал бы тусклее, когда конденсатор достиг полного напряжения.
Время разрядки конденсатора
Когда мы обеспечиваем путь для разрядки конденсатора, электроны покидают конденсатор, и напряжение на конденсаторе уменьшается. Он не разряжается мгновенно, а следует экспоненциальной кривой. Мы разделяем эту кривую на 6 сегментов, но нас интересуют только первые 5. В точке 1 напряжение всегда равно 36,8%, в точке 2 будет 13,5%, в точке 3 будет 5%, в точке 4 будет 1,8% и в точке 5 будет 0,7%.
Например, если бы у нас была батарея на 9 В, лампа с сопротивлением 500 Ом и конденсатор на 2000 мкФ, наша постоянная времени была бы 500 Ом, умноженная на 0,002 фарад, что составляет 1 секунду.
Итак, в тот самый момент, когда батарея отключена, конденсатор будет на 9 В, и, поскольку он питает цепь, лампа также будет. Через 1 постоянную времени, в данном случае 1 секунду, напряжение составит 36,8%, что составляет 3,312 В, через 2 секунды — 1,215 В, через 3 секунды — 0,45 В, через 4 секунды — 0,162 В и через 5 секунд — 0,063 В.
Таким образом, лампа будет гореть чуть менее 3 секунд. Явно становится тусклее.
8.1 Конденсаторы и емкости — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объяснить понятия конденсатора и его емкости
- Опишите, как оценить емкость системы проводников
Конденсатор — это устройство, используемое для хранения электрического заряда и электрической энергии. Конденсаторы обычно имеют два электрических проводника, разделенных расстоянием. (Обратите внимание, что такие электрические проводники иногда называют «электродами», но правильнее было бы назвать их «пластинами конденсатора».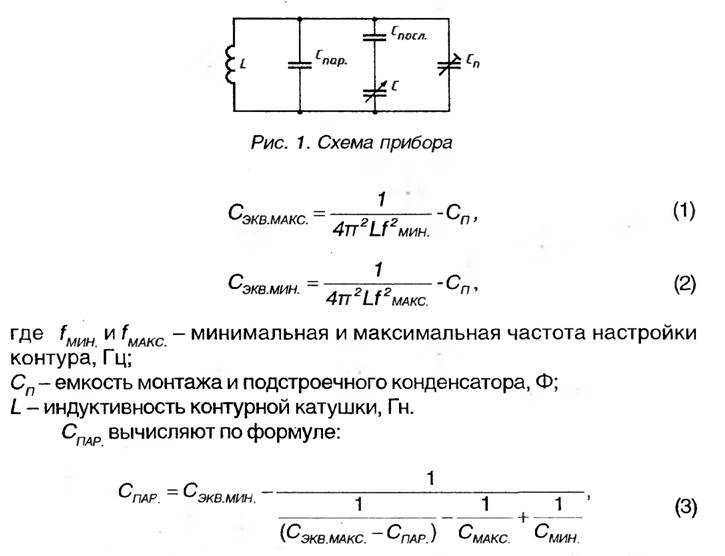
) Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор называется «вакуумный конденсатор». Однако это пространство обычно заполнено изоляционным материалом, известным как диэлектрик. (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем памяти в конденсаторе определяется свойством, называемым
Применение конденсаторов варьируется от фильтрации статического электричества от радиоприема до накопления энергии в сердечных дефибрилляторах. Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 8.2. В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к изначально незаряженному конденсатору, потенциал батареи перемещает небольшое количество заряда величиной 9.0121 Q
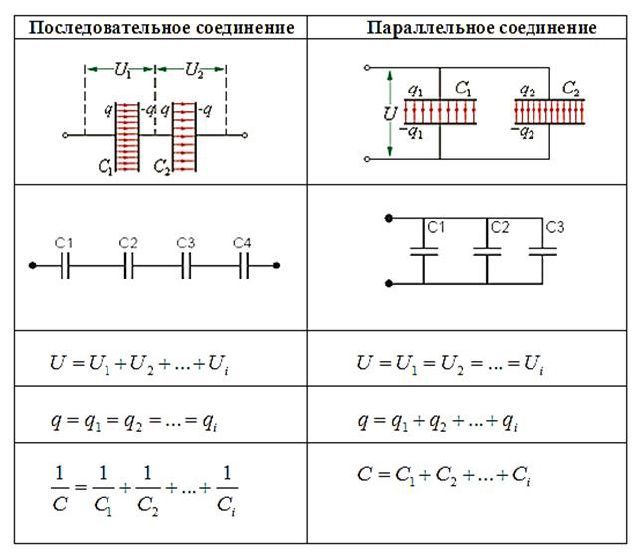Конденсатор в целом остается нейтральным, но с зарядами +Q+Q и -Q-Q, расположенными на противоположных пластинах.Рисунок 8.2 Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них на пластинах есть заряды +Q+Q и −Q−Q (соответственно). (a) Конденсатор с плоскими пластинами состоит из двух пластин противоположного заряда площадью A , разделенных расстоянием d . (b) Скрученный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).
Система, состоящая из двух одинаковых пластин с параллельными проводниками, разделенных расстоянием, называется конденсатором с параллельными пластинами (рис. 8.3). Величина электрического поля в пространстве между параллельными пластинами равна E=σ/ε0E=σ/ε0, где σσ — поверхностная плотность заряда на одной пластине (напомним, что σσ — заряд Ом , приходящийся на площадь поверхности А).
). Таким образом, величина поля прямо пропорциональна Q .
Рисунок 8.3 Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности пластин конденсатора. Линии электрического поля в конденсаторе с плоскими пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.
Конденсаторы с разными физическими характеристиками (такими как форма и размер их пластин) сохраняют разное количество заряда при одном и том же приложенном на их пластинах напряжении В . Емкость C конденсатора определяется как отношение максимального заряда Q , который может храниться в конденсаторе, к приложенному напряжению В на его обкладках. Другими словами, емкость — это наибольшее количество заряда на вольт, которое может храниться на устройстве:
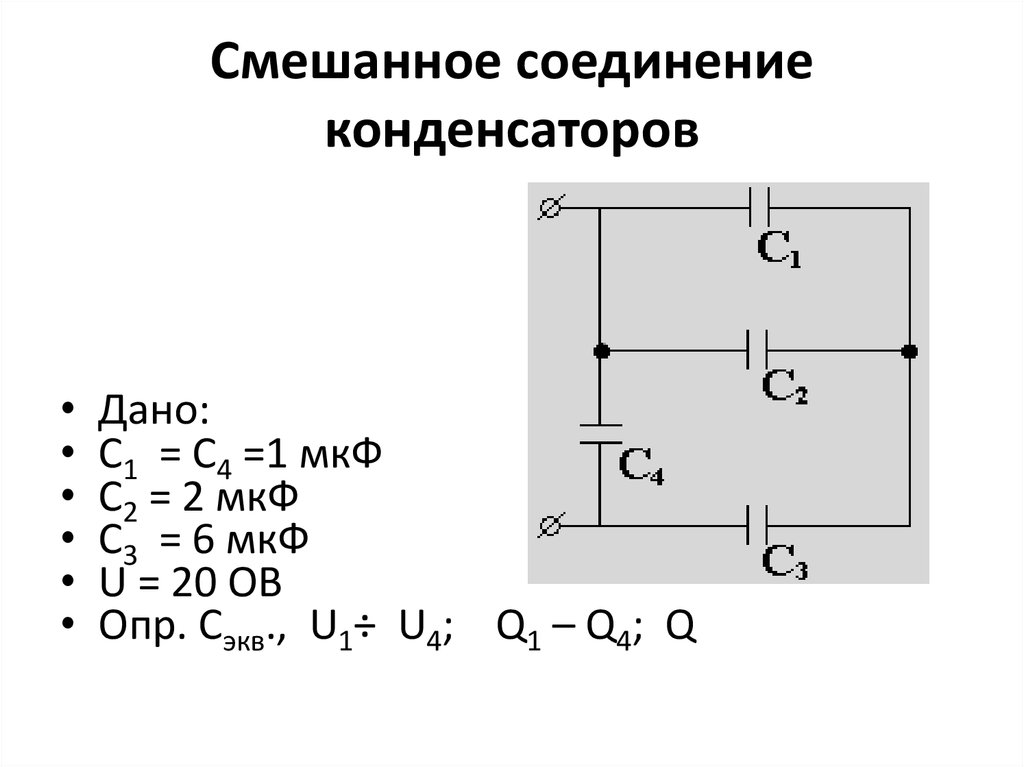C=QV.
C=QV.
8.1
Единицей измерения емкости в системе СИ является фарад (Ф), названный в честь Майкла Фарадея (1791–1867). Поскольку емкость — это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или
1F=1C1V.1F=1C1V.
По определению, конденсатор емкостью 1,0 Ф способен хранить 1,0 Кл заряда (очень большой заряд), когда разность потенциалов между его пластинами составляет всего 1,0 В. Таким образом, один фарад — это очень большая емкость. Типичные значения емкости находятся в диапазоне от пикофарад (1 пФ = 10–12 Ф) (1 пФ = 10–12 Ф) до миллифарад (1 мФ = 10–3 Ф) (1 мФ = 10–3 Ф), включая микрофарад (1 мкФ = 10–6 Ф1 мкФ = 10–10–3). 6F). Конденсаторы могут изготавливаться различных форм и размеров (рис. 8.4).
Рисунок 8.4 Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно связан со значением его емкости. (кредит: Windell Oskay)
Расчет емкости
Мы можем рассчитать емкость пары проводников с помощью следующего стандартного подхода.
Стратегия решения проблем
Расчет емкости
- Предположим, что конденсатор имеет заряд Q .
- Определите электрическое поле E→E→ между проводниками. Если в расположении проводников присутствует симметрия, вы можете использовать закон Гаусса для этого расчета.
- Найдите разность потенциалов между проводниками из
VB-VA=-∫ABE→·dl→, VB-VA=-∫ABE→·dl→,
8,2
где путь интегрирования ведет от одного проводника к другому. Тогда величина разности потенциалов равна V=|VB-VA|V=|VB-VA|. - Зная В , получите емкость непосредственно из уравнения 8.1.
Чтобы показать, как работает эта процедура, мы теперь рассчитаем емкости пластинчатых, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.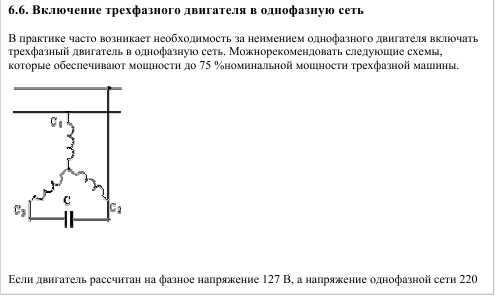
Конденсатор с параллельными пластинами
Конденсатор с плоскими пластинами (рис. 8.5) имеет две одинаковые проводящие пластины, каждая из которых имеет площадь поверхности A , разделенные расстоянием d . При напряжении В подается на конденсатор, он накапливает заряд Q , как показано на рисунке. Мы можем видеть, как его емкость может зависеть от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить. Таким образом, C должно быть больше для большего значения A . Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов.
Следовательно, C должен быть больше для меньшего d .
Рисунок 8,5 В плоском конденсаторе с пластинами, расположенными на расстоянии d , каждая пластина имеет одинаковую площадь поверхности A .
Определим поверхностную плотность заряда σσ на пластинах как
σ=QA.σ=QA.
Из предыдущих глав мы знаем, что когда d мало, электрическое поле между пластинами достаточно однородно (без учета краевых эффектов) и что его величина определяется выражением
E=σε0,E=σε0,
, где константа ε0ε0 — диэлектрическая проницаемость свободного пространства, ε0=8,85×10−12F/м.ε0=8,85×10−12F/м. Единица СИ Ф/м эквивалентна C2/N·m2.C2/N·m2. Поскольку электрическое поле E→E→ между пластинами однородно, разность потенциалов между пластинами равна
.V=Ed=σdε0=Qdε0A.V=Ed=σdε0=Qdε0A.
Следовательно, уравнение 8.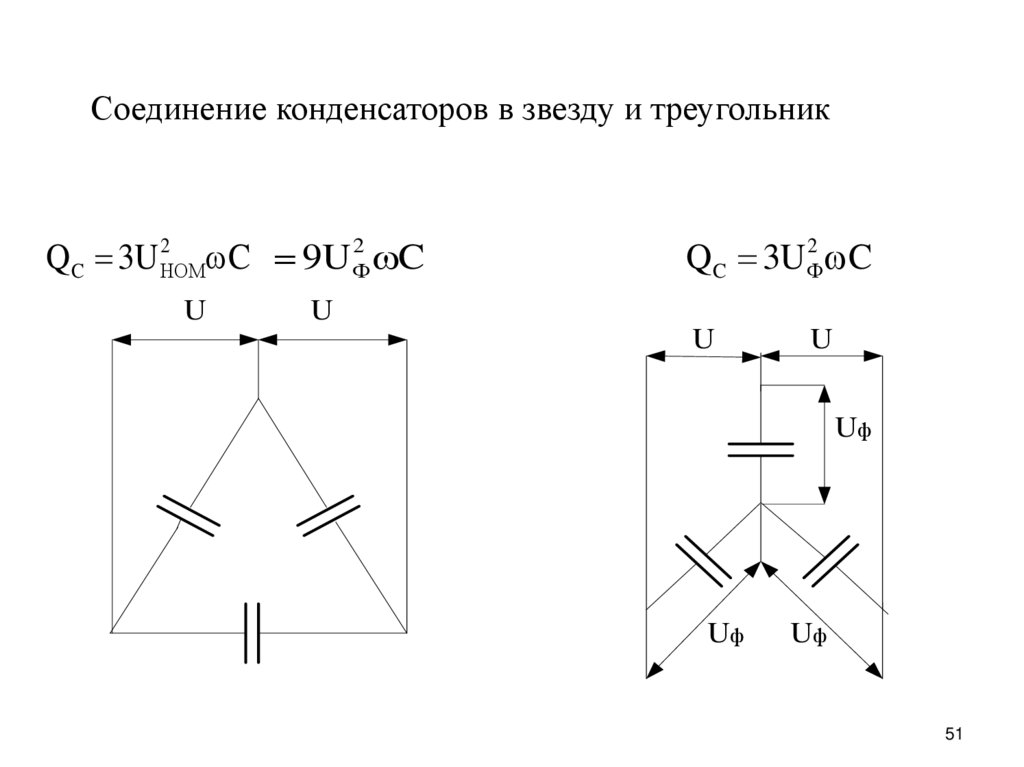
1 дает емкость плоского конденсатора как
C=QV=QQd/ε0A=ε0Ad.C=QV=QQd/ε0A=ε0Ad.
8,3
Обратите внимание, что из этого уравнения емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора. На самом деле это верно не только для плоского конденсатора, но и для всех конденсаторов: Емкость не зависит от Q или V . При изменении заряда соответственно изменяется и потенциал, так что Q / V остается постоянным.
Пример 8.1
Емкость и заряд, хранящиеся в конденсаторе с параллельными пластинами
а) Какова емкость пустого плоского конденсатора с металлическими пластинами площадью 1,00 м21,00 м2, разделенными расстоянием 1,00 мм? б) Сколько заряда накопится в этом конденсаторе, если к нему приложить напряжение 3,00×103 В3,00×103 В?
Стратегия
Нахождение емкости C является прямым применением уравнения 8.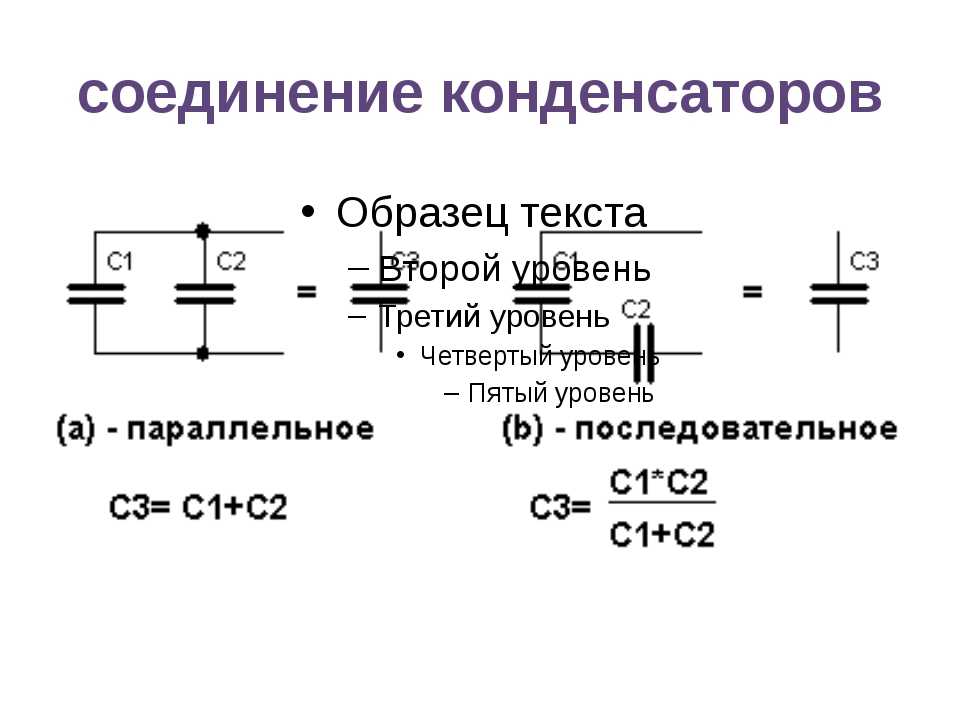
3. Как только мы найдем C , мы сможем найти накопленный заряд, используя уравнение 8.1.
Решение
- Ввод данных значений в уравнение 8.3 дает
C=ε0Ad=(8,85×10−12Fm)1,00m21,00×10−3m=8,85×10−9F=8,85nF.C=ε0Ad=(8,85×10−12Fm)1,00m21,00×10−3m= 8,85×10-9Ф=8,85нФ.
Это маленькое значение емкости указывает на то, насколько сложно сделать устройство с большой емкостью. - Инвертирование уравнения 8.1 и ввод известных значений в это уравнение дает
Q=CV=(8,85×10-9F)(3,00×103В)=26,6мкКл. Q=CV=(8,85×10-9F)(3,00×103В)=26,6мкКл.
Значение
Этот заряд лишь немного больше, чем в типичных приложениях статического электричества. Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около 3,0 МВ/м, на этом конденсаторе больше не может накапливаться заряд при увеличении напряжения.
Пример 8.
2A 1-F Конденсатор с параллельными пластинами
Предположим, вы хотите построить конденсатор с плоскими пластинами емкостью 1,0 Ф. Какую площадь вы должны использовать для каждой пластины, если расстояние между пластинами составляет 1,0 мм?
Решение
Преобразуя уравнение 8.3, мы получаем
A=Cdε0=(1,0F)(1,0×10-3м)8,85×10-12F/м=1,1×108м2.A=Cdε0=(1,0F)(1,0×10-3м)8,85×10-12F/ м=1,1×108м2.
Каждая квадратная пластина должна иметь диаметр 10 км. Раньше было обычной шуткой просить студента пойти на склад лаборатории и попросить конденсатор с плоскими пластинами 1-Ф, пока обслуживающему персоналу не надоела эта шутка.
Проверьте свое понимание 8.1
Емкость плоского конденсатора составляет 2,0 пФ. Если площадь каждой пластины 2,4 см22,4 см2, каково расстояние между пластинами?
Проверьте свое понимание 8.
2Убедитесь, что σ/Vσ/V и ε0/dε0/d имеют одинаковые физические единицы.
Сферический конденсатор
Сферический конденсатор представляет собой еще один набор проводников, емкость которых можно легко определить (рис. 8.6). Он состоит из двух концентрических проводящих сферических оболочек радиусами R1R1 (внутренняя оболочка) и R2R2 (внешняя оболочка). Оболочки получают равные и противоположные заряды +Q+Q и −Q−Q соответственно. Из-за симметрии электрическое поле между оболочками направлено радиально наружу. Мы можем получить величину поля, применив закон Гаусса к сферической поверхности Гаусса радиусом 9dr)=Q4πε0∫R1R2drr2=Q4πε0(1R1−1R2).
В этом уравнении разность потенциалов между пластинами равна V=-(V2-V1)=V1-V2V=-(V2-V1)=V1-V2. Подставим этот результат в уравнение 8.1, чтобы найти емкость сферического конденсатора:
C=QV=4πε0R1R2R2−R1.C=QV=4πε0R1R2R2−R1.
8,4
Рисунок
8,6
Сферический конденсатор состоит из двух концентрических проводящих сфер.
Обратите внимание, что заряды проводника находятся на его поверхности.
Пример 8.3
Емкость изолированной сферы
Рассчитайте емкость одиночной изолированной проводящей сферы радиусом R1R1 и сравните ее с уравнением 8.4 в пределе, когда R2→∞R2→∞.
Стратегия
Мы предполагаем, что заряд на сфере равен Q , и поэтому мы следуем четырем шагам, описанным ранее. Мы также предполагаем, что другой проводник представляет собой концентрическую полую сферу бесконечного радиуса.
Раствор
Снаружи изолированной проводящей сферы электрическое поле определяется уравнением 8.2. Величина разности потенциалов между поверхностью изолированной сферы и бесконечностью равна 9dr)=Q4πε0∫R1+∞drr2=14πε0QR1.
Таким образом, емкость изолированной сферы равна
C=QV=Q4πε0R1Q=4πε0R1.
C=QV=Q4πε0R1Q=4πε0R1.
Значение
Тот же результат можно получить, взяв предел уравнения 8.4 при R2→∞R2→∞. Таким образом, отдельная изолированная сфера эквивалентна сферическому конденсатору, внешняя оболочка которого имеет бесконечно большой радиус.
Проверьте свое понимание 8.3
Радиус внешней сферы сферического конденсатора в пять раз больше радиуса его внутренней оболочки. Каковы размеры этого конденсатора, если его емкость 5,00 пФ?
Цилиндрический конденсатор
Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров (рис. 8.7). Внутренний цилиндр радиусом R1R1 может быть как оболочкой, так и сплошным телом. Внешний цилиндр представляет собой оболочку с внутренним радиусом R2R2. Мы предполагаем, что длина каждого цилиндра равна l и что избыточные заряды +Q+Q и −Q−Q располагаются на внутреннем и внешнем цилиндрах соответственно.
Рисунок 8,7 Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров. Здесь заряд на внешней поверхности внутреннего цилиндра положителен (обозначен ++), а заряд на внутренней поверхности внешнего цилиндра отрицателен (обозначен —). 9dr)=Q2πε0l∫R1R2drr=Q2πε0llnr|R1R2=Q2πε0llnR2R1.
Таким образом, емкость цилиндрического конденсатора равна
C=QV=2πε0lln(R2/R1).C=QV=2πε0lln(R2/R1).
8,6
Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением уравнения 8.6 является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов. Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом. (Здесь мы предполагаем вакуум между проводниками, но физика качественно почти такая же, когда пространство между проводниками заполнено диэлектриком.
) Такая конфигурация экранирует электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний проводник обычно заземлен. Теперь из уравнения 8.6 емкость на единицу длины коаксиального кабеля равна
Cl=2πε0ln(R2/R1).Cl=2πε0ln(R2/R1).
В практических приложениях важно выбрать конкретные значения C / l . Этого можно добиться соответствующим выбором радиусов проводников и изоляционного материала между ними.
Проверьте свое понимание 8.4
Когда цилиндрический конденсатор получает заряд 0,500 нКл, между цилиндрами измеряется разность потенциалов 20,0 В. а) Чему равна емкость этой системы? б) Чему равно отношение их радиусов, если длина цилиндров 1,0 м?
На рис. 8.4 показаны несколько типов практических конденсаторов.
Обычные конденсаторы часто изготавливают из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. рис. 8.2(b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторыми распространенными изоляционными материалами являются слюда, керамика, бумага и антипригарное покрытие Teflon™.
Другим популярным типом конденсатора является электролитический конденсатор. Он состоит из окисленного металла в токопроводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость алюминиевого электролитического конденсатора одного типа может достигать 1,0 Ф. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста.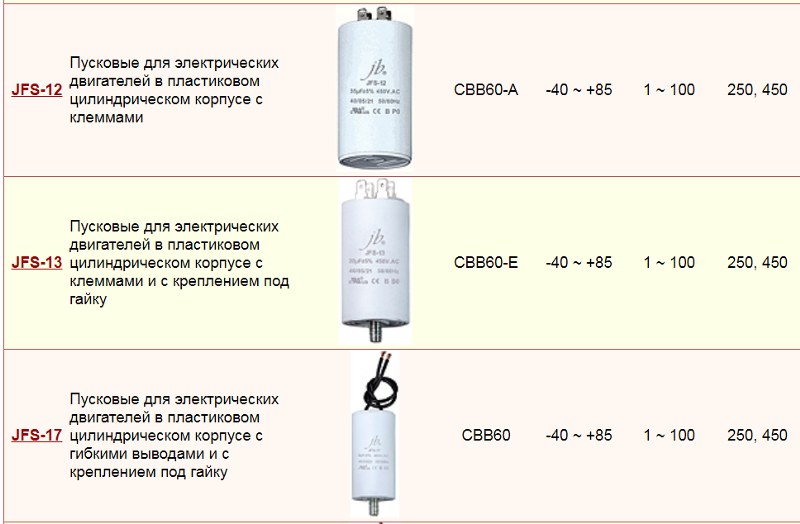
Когда возникает обратная поляризация, электролитическое воздействие разрушает оксидную пленку. Конденсатор этого типа нельзя подключать к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет полярность (см. Цепи переменного тока в цепях переменного тока).
Переменный воздушный конденсатор (рис. 8.8) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначен как «ротор»). Поворачивая вал, можно изменить площадь поперечного сечения в области нахлеста пластин; следовательно, емкость этой системы может быть настроена на желаемое значение. Конденсаторная настройка находит применение в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильный радиоприемник на любимую станцию, подумайте о емкости.
Рисунок
8,8
В переменном воздушном конденсаторе емкость можно регулировать, изменяя эффективную площадь пластин.
(кредит: модификация работы Робби Спроула)
Символы, показанные на рис. 8.9, представляют собой схемы различных типов конденсаторов. Обычно мы используем символ, показанный на рис. 8.9(а). Символ на рис. 8.9(c) обозначает конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией плоского конденсатора. Электролитический конденсатор представлен символом в части рисунка 8.9.(б), где изогнутая пластина указывает на отрицательную клемму.
Рисунок 8,9 Это показывает три различных представления схемы конденсаторов. Символ в (а) является наиболее часто используемым. Символ в (b) представляет собой электролитический конденсатор. Символ в (c) представляет собой конденсатор переменной емкости.
Интересный прикладной пример модели конденсатора взят из клеточной биологии и касается электрического потенциала плазматической мембраны живой клетки (рис. 8.10). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым избранным ионам проходить внутрь или наружу клетки.