Формула расчета площади прямоугольника в м2: Онлайн калькулятор. Площадь прямоугольника — Концессии и государственно-частное партнерство в ЖКХ

Содержание

Как рассчитать площадь прямоугольника в квадратных метрах

Прямоугольник – это четырехугольник, у которого все углы равны 90 градусам (прямые). Основными математичскими характеристиками прямоугольника являются длины его сторон.

Формула расчета площади прямоугольника:

S – площадь прямоугольника;
a – длина прямоугольника;
b – ширина прямоугольника.

Быстро выполнить эту простую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор для рассчета площади прямоугольника в квадратных метрах. С помощью этой программы вы в один клик сможете рассчитать площадь прямоугольника в м2, если известны его длина и ширина.

На данной странице калькулятор поможет рассчитать площадь прямоугольника онлайн. Для расчета задайте длину сторон или длины диагоналей и угол между ними.

Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).

Через стороны

Формула для нахождения площади прямоугольника через стороны:

Через диагонали и угол между ними

Формула для нахождения площади прямоугольника через диагонали и угол между ними:

При ремонте, покупке материалов нужно знать площадь помещений. Говорят еще «квадратура». Как посчитать площадь комнаты в квадратных метрах, что для этого нужно — будем рассматривать в статье.

Немного теории

Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.

Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний

Что такое 1 см² и 1 м²

Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.

Что такое один квадратный сантиметр

Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м². В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².

Формулы

Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.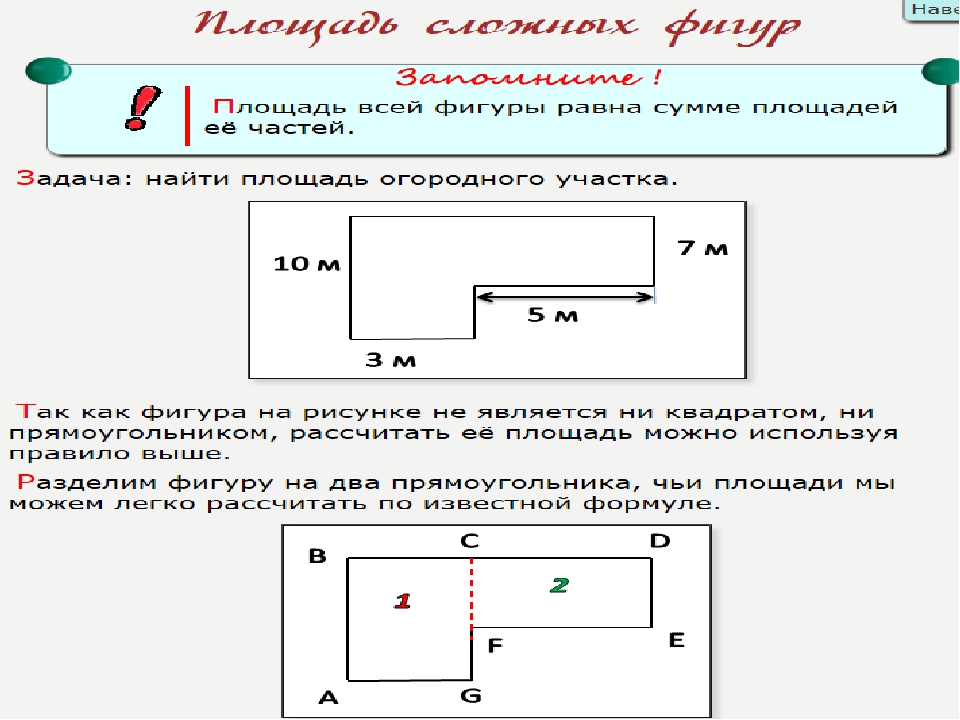

При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата

Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.

Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².

В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.

Простейший калкулятор для расчета площади прямоугольной комнаты.

Перевод квадратных сантиметров в квадратные метры

Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:

80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².
60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².

Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.

Соотношение квадратных сантиметров и квадратных метров

Если же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:

4000 см² / 10000 = 0,4 м²;
96000 см² / 10000 = 9,6 м²;
3600 см²/ 10000 = 0,36 м².

Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно.

Нужно будет предварительно провести измерения, а потом заняться расчетами.

Как посчитать площадь комнаты в квадратных метрах

Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).

Можно найти площадь комнаты зная длину и ширину

Измерения

Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.

На схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.

Как высчитать квадратуру комнаты

Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола. Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку. Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.

Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры.

Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.

Как найти площадь комнаты сложной формы

Считаем большой прямоугольник: 5 м * 4,35 м = 21,75 м².
Находим квадратуру маленького: 2,5 м * 2,65 м = 6,625 м².
Площадь пола в этом помещении равна сумме 21,75 м² + 6,625 м² = 28,375 м².

При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.

Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.

Получается, ищем площадь трех прямоугольников

А недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.

Приведем пример расчета подставляя произвольные значения:

Большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Для простоты округлим до 3,38 м².
Средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м². Снова округлим до 0,67 м².

Самый маленький прямоугольник (в нашем случае это будет квадрат): 0,57 м *0,57 м = 0,3249 м2, после округления имеем 0,33 м².
Чтобы найти общую площадь складываем квадратуру двух прямоугольников и добавляем половину площади последнего, самого маленького участка. 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.

Площадь квартиры

Так как ремонт — это «бедствие», которое периодически нас посещает, лучше сделать план всей квартиры с подробными замерами.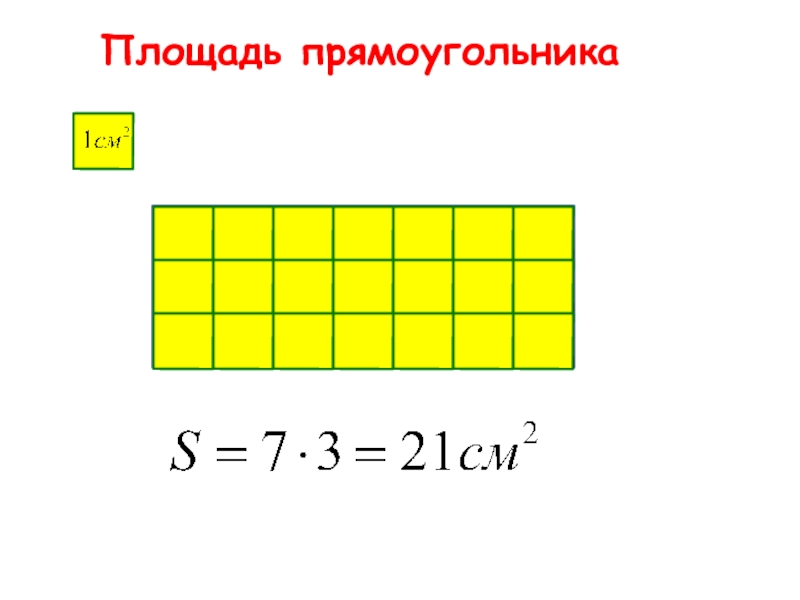

На этом же плане проставьте площади каждого помещения. После того, как рассчитаете квадратуру всех комнат, сложите цифры и получите метраж квартиры.

Для плана лучше рассчитать метраж каждой комнаты

Один вариант может быть как на рисунке выше — для того, чтобы знать именно площади каждого помещения. Это потребуется для закупки материалов. Но нужен будет еще план, на котором будут все длины. Простенки, ширина окон, дверей и т.д. Это потребуется, например, для разработки схем укладки ламината, напольной плитки или других покрытий. Нужен будет такой план и при планировании теплого пола.

Есть, кстати, приложение-калькулятор для телефона, при помощи которого все вычисления сделать очень просто.

Формула расчета площади прямоугольника в м2

Формула расчета площади прямоугольника:

S – площадь прямоугольника;
a – длина прямоугольника;
b – ширина прямоугольника.

Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).

Через стороны

Формула для нахождения площади прямоугольника через стороны:

Через диагонали и угол между ними

Формула для нахождения площади прямоугольника через диагонали и угол между ними:

Начиная ремонт, первым делом нужно определить необходимое количество строительных материалов. Провести расчеты могут специалисты, которые будут выполнять работы. Но они часто делают вычисления с большой погрешностью в свою пользу. Рассмотрим, как самостоятельно посчитать площадь стен.

Инструменты для подсчета квадратных метров

Для расчетов понадобятся:

уровень строительный;
рулетка с ограничителем;
длинная линейка и угольник;
карандаш и бумага;
калькулятор.

Для нанесения размеров нарисуем схему комнат. Обозначим двери, окна, ниши, выступы. Результаты замеров нанесем на чертеж.

Как рассчитать площадь прямоугольных стен

Измеряем высоту (h), длину (a), ширину (b).

Площадь: S = P × h

Периметр: P = (a + b) × 2

Вдоль плинтуса измеряем длину и ширину помещений.

Высоту — по вертикальному углу.

Р = (5 + 4) × 2 = 18 м;

Как правильно рассчитать площадь стен со сложной поверхностью

Не все помещения имеют строгую прямоугольную форму. В зданиях часто присутствуют замысловатые архитектурные элементы, усложняющие расчет.

Как посчитать квадратуру стен за вычетом проемов

При определении точного объема работ, вычтем размеры окон и дверей из общего количества квадратных метров стен комнаты. Для этого по краю рамы замеряем ширину и высоту окна, по краю коробки — габариты двери.

Перемножив длину и ширину проемов, получаем размер, который необходимо вычесть.

Аналогично действуем, если из подсчитываемой квадратуры комнаты нужно исключить печи, камины, радиаторы.

В помещении имеется окно 2,5 м × 1,5 м и дверь 0,9 м × 2,1 м.

S окна равна 2,5 × 1,5 = 3,75 м².

S двери равна 0,9 × 2,1 = 1,89 м².

S стен за вычетом проемов составляет 54 − 3,75 − 1,89 = 48,36 м².

Определение площади помещений неправильной формы

Для определения периметра зданий любых конфигураций сложим длины всех стен, включая выступы и ниши.

Проводить измерения помещений неправильной формы можно, разбив поверхность на несколько простых фигур.

Если у вас комната с прямоугольным выступом, вы имеете две фигуры, квадратуру которых легко вычислить, затем сложить.

Если элемент содержит в себе полукруг, для расчета нужно разбить его на полукруг и прямоугольник.

Как считать квадратные метры стен с круглыми элементами

Встречаются круглые и полукруглые жилые здания или строения с элементами окон или дверей в виде арки.

Их периметр можно определить, умножив диаметр на число π (Пи) = 3,14.

Квадратуру вертикальных поверхностей определяем, умножив полученное значение на высоту от пола до потолка.

S круга равна квадрату радиуса, умноженному на число π; полукруга — половине этой величины.

Если необходимо из квадратуры комнаты вычесть площадь круглых колонн или полукруглых выступающих элементов, при невозможности измерить диаметр или радиус, измеряем длину окружности (P) и применяем формулу: S = P² / 4π.

Как рассчитать квадратные метры конструкций в виде треугольника

В случае наличия комнаты с треугольными элементами, мы можем применить несколько формул, в зависимости от вида фигур:

Где a, b, c — длины сторон треугольника; p — периметр.

Объем помещения

Для определения объема необходимо высчитать площадь пола, и полученный показатель перемножить на высоту. V = S × h.

Расчет площади стен дома на калькуляторе

Существенно облегчат расчеты специальные программы, к которым относится строительный калькулятор в онлайн-версии.

Чтобы посмотреть, сколько квадратных метров составляют стены за вычетом проемов, достаточно выбрать геометрическую форму помещения и ввести показатели:

ширину;
длину;
высоту;
количество проемов;
размеры окон и дверей.

Строительный калькулятор рассчитает количество отделочных материалов, необходимых для вашего ремонта.

Советы и рекомендации

Необходимо помнить, что геометрические параметры зданий редко могут быть идеальными. Поэтому для определения точных величин замеры лучше производить в нескольких местах, а затем выводить среднее арифметическое. Например, рассчитывая площадь комнаты по стенам, длину лучше измерять по потолку, плинтусу и в середине вертикальной плоскости. Высоту — в углах и середине стены по отвесу.

Чтобы вычислить периметр при наличии множества выступов и ниш разных форм, необходимо проложить вдоль всех элементов шнур, затем измерить его рулеткой.

Подсчитав точные параметры, можно идти в магазин за строительными материалами. Лучше показать схемы с нанесенными размерами продавцу-консультанту. Специалист поможет рассчитать расход материалов с учетом нахлеста, подбора рисунка обоев или потерь при резке плитки.

150

Площадь треугольника

Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей треугольников.

Таблица с формулами площади треугольника (в конце страницы)

Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)

— Вычисления (показано) (скрыто)

— примечания (показано) (скрыто)

Для всех треугольников

Площадь треугольника по основанию и высоте

Сторона a

Высота h

Основанием треугольника может быть выбрана любая из сторон треугольника.

Площадь треугольника по двум сторонам и углу между ними

Сторона a

Сторона b

Угол α° между сторонами a и b

Угол α между сторонами может быть любым: тупым, острым, прямым.

Площадь треугольника по радиусу вписанной окружности и трем сторонам

Сторона a

Сторона b

Сторона c

Радиус r вписанной окружности

Площадь треугольника по радиусу описанной окружности и трем сторонам

Сторона a

Сторона b

Сторона c

Радиус R описанной окружности

Площадь треугольника по формуле Герона

Полупериметр:

Сторона a

Сторона b

Сторона c

Площадь произвольного треугольника по стороне и двум прилежащим углам

Сторона a

Угол β°

Угол α°

Для равнобедренных треугольников

Площадь равнобедренного треугольника по боковым сторонам и основанию

Сторона a (a = b)

Сторона c

Площадь равнобедренного треугольника по боковым сторонам и углу между ними

Боковая сторона a (a = b)

Угол α° между боковыми сторонами

Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними

Боковая сторона a (a = b)

Основание треугольника c

Угол β° между основанием и стороной

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами

Основание треугольника c

Угол α° между боковыми сторонами

Для равносторонних треугольников

Площадь равнобедренного треугольника по высоте и основанию

Основание треугольника c

Высота h

Площадь равностороннего треугольника по стороне

Сторона a (a = b = c)

Площадь равностороннего треугольника по высоте

Высота h

Площадь равностороннего треугольника по радиусу вписанной окружности

Радиус r вписанной окружности

Площадь равностороннего треугольника по радиусу описанной окружности

Радиус R описанной окружности

Для прямоугольных треугольников

Площадь прямоугольного треугольника по двум катетам

Катет a

Катет b

Площадь прямоугольного треугольника через гипотенузу и угол

Сторона c

Угол α

Площадь прямоугольного треугольника через катет и угол

Сторона b

Угол α

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

Отрезок d

Отрезок e

Площадь прямоугольного треугольника через гипотенузу и вписанную окружность

Сторона с

Радиус r

Площадь прямоугольного треугольника по формуле Герона

Полупериметр:

Сторона a

Сторона b

Сторона c

Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.

Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.

В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.

Таблица с формулами площади треугольника

Определения

Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

Скачать формулы площади треугольника в виде картинки

Как вычислить площадь прямоугольника. Площадь прямоугольника

Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.

Важно! Важ участок должен приблизительно вписываться в окружность. Иначе расчеты будут не совсем точными.

Указываем все данные в метрах

A B, D A, C D, B C — Размер каждой стороны делянки.

Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.

Методика определения размеров участка ручным методом

Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков. Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.

Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².

После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.

В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах. Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.

Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.

Общие данные

Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.

Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).

На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.

Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.

И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.

Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.

Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.

Площадь комнаты в квадратных метрах

Рулетка. Лучше — с фиксатором, но подойдет и обычная.
Бумага и карандаш или ручка.
Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы

Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.

В этом случае порядок вычислений такой:

Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

высота потолков;
высота и ширина дверных проемов;
высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
Стена с окном:
1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,75 кв.м.
3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

Объем комнаты

Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:

длинна — 5,6 м;
ширина — 3,2 м;
высота — 2,5 м.

Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м 3 . Итак, объем помещения 44,8 куба.

L * H = S чтобы найти площадь прямоугольника, необходимо перемножить ширину на длину. Другими словами её можно выразить так: площадь прямоугольника равна произведению сторон .

1. Приведём пример расчёта как найти площадь прямоугольника , стороны равны известным величинам, например ширина 4 см, длина 8 см.

Как найти площадь прямоугольника со сторонами 4 и 8 см: Решение простое! 4 х 8 = 32 см2 . Чтобы решить такую простую задачу нужно вычислить произведение сторон прямоугольника или просто умножить ширину на длину, это и будет площадь!

2. Частным случаем прямоугольника является квадрат, это тот случай когда стороны у прямоугольника равны, в этом случае найти площадь квадрата можно по выше приведённой формуле.

Чему равна площадь прямоугольника?

Умение рассчитывать площадь прямоугольника является базовым навыком для решения огромного количества бытовых или технических задач.2$.

Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника. Средняя оценка: 4.4 . Всего получено оценок: 214.

Урок на тему: «Формулы определения площади треугольника, прямоугольника, квадрата»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику И.И.Зубаревой и А.Г.Мордковича
Тренажер к учебнику Г.В.Дорофеева и Л.Г.Петерсона

Определение и понятие площади фигуры

Чтобы лучше понять, что такое площадь фигуры, рассмотрим рисунок.
Эта произвольная фигура разбита на 12 маленьких квадратика. Сторона каждого квадратика равна 1 см. А площадь каждого квадратика равна 1 квадратному сантиметру, что записывается так: 1 см 2 .

Тогда площадь фигуры равна 12 квадратным сантиметрам. В математике площадь обозначается латинской буквой S.
Значит, площадь нашей фигуры равна: S фигуры = 12 см 2 .

Площадь фигуры равна площади всех маленьких квадратиков, из которых она состоит!

Ребята, запомните!
Площадь измеряется квадратными единицами длины. Единицы измерения площади:
1. Квадратный километр — км 2 (когда площади очень большие, например, страна или море).
2. Квадратный метр — м 2 (вполне подходит для того, чтобы измерять площадь участка или квартиры).
3. Квадратный сантиметр — см 2 (обычно используется на уроках математики, когда рисуют фигуры в тетради).
4. Квадратный миллиметр — мм 2 .

Площадь треугольника

Рассмотрим два вида треугольников: прямоугольный и произвольный.

Чтобы найти площадь прямоугольного треугольника необходимо знать длину основания и высоту. В прямоугольном треугольнике высоту заменяет одна из сторон. Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон.
В нашем примере стороны равны 7 см и 4 см. Формула для расчета площади треугольника записывается так:
S прямоугольного треугольника АВС = ВС * СА: 2

S прямоугольного треугольника АВС = 7 см * 4 см: 2 = 14 см 2

Теперь рассмотрим произвольный треугольник.

Для такого треугольника необходимо провести высоту к основанию.
В нашем примере высота равна 6 см, а основание равно 8 см. Как и в предыдущем примере, рассчитываем площадь по формуле:
S произвольного треугольника АВС = ВС * h: 2.

Подставим в формулу наши данные и получим:
S произвольного треугольника АВС = 8 см * 6 см: 2 = 24 см 2 .

Площадь прямоугольника и квадрата

Возьмем прямоугольник АВСD со сторонами 5 см и 8 см.
Формула расчета площади прямоугольника записывается так:
S прямоугольника АВСD = АВ * ВС.

S прямоугольника АВСD = 8 см * 5 см = 40 см 2 .

Теперь рассчитаем площадь квадрата. В отличии от прямоугольника и треугольника, для нахождения площади квадрата необходимо знать только одну сторону. В нашем примере сторона квадрата ABCD равна 9 см. S квадрата АВСD = АВ * ВС = АВ 2 .

Подставим в формулу наши данные и получим:
S квадрата АВСD = 9 см * 9 см = 81 см 2 .

Как найти площадь прямоугольника формула 3. Площадь прямоугольника онлайн калькулятор. Как найти площадь прямоугольника

Площадь многоугольника

Понятие площади многоугольника будем связывать с такой геометрической фигурой, как квадрат. За единицу площади многоугольника будем принимать площадь квадрата со стороной, равной единице. Введем два основных свойства, для понятия площади многоугольника.

Свойство 1: Для равных многоугольников значения их площадей равны.

Свойство 2: Любой многоугольник можно разбить на несколько многоугольников. При этом площадь исходного многоугольника равняется сумме площадей всех многоугольников, на которые разбит данный многоугольник.

Площадь квадрата

Теорема 1

Площадь квадрата определяется как квадрат длины его стороны.

где $a$ — длина стороны квадрата.

Доказательство.

Для доказательства нам необходимо рассмотреть три случая.

Теорема доказана.

Площадь прямоугольника

Теорема 2

Площадь прямоугольника определяется произведением длин его смежных сторон.

Математически это можно записать следующим образом

Доказательство.

Пусть нам дан прямоугольник $ABCD$, у которого $AB=b,\ AD=a$. Достроим его до квадрата $APRV$, длина стороны которого равняется $a+b$ (рис. 3).

Рисунок 3.

По второму свойству площадей имеем

\ \ \

По теореме 1

\ \

Теорема доказана.

Пример задач

Пример 1

Найти площадь прямоугольника со сторонами $5$ и $3$.

Для вычисления площади и периметра квадрата нужно разобраться в понятиях этих величин. Квадрат представляет собой прямоугольник только с четырьмя одинаковыми сторонам, которые имеют между собой угол в 90°. Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.

Площадь квадрата и как ее найти

Как было сказано выше, квадрат — это прямоугольник, имеющий 4 равные стороны, поэтому ответом на вопрос: «как найти площадь квадрата» является формула: S = a*a или S = a 2 , где а — сторона квадрата. Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.

Например, S = 121, следовательно, а = √121 = 11. Если заданное значение отсутствует в таблице квадратов, то можно воспользоваться калькулятором: S = 94, а = √94 = 9,7.

Как найти периметр квадрата

Периметр квадрата находится по легкой формуле: Р = 4а, где а — сторона квадрата.

Пример:

сторона квадрата = 5, следовательно, P = 4*5 = 20
сторона квадрата = 3, следовательно, Р = 4*3 = 12

Но существуют такие задачи, где заведомо обозначена площадь, а нужно найти периметр. При решении нужны формулы, которые представлены ранее.

Например: как найти периметр квадрата, если известна площадь, равная 144?

Шаги решения:

Выясняем длину одной стороны: а = √144 = 12
Находим периметр: Р = 4*12 = 48.

Нахождение периметра вписанного квадрата

Существуют еще несколько способов нахождения периметра квадрата. Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.

Алгоритм решения:

так как на рассмотрении квадрат, формулу можно выразить таким образом: a 2 + a 2 = (2r) 2 ;
затем следует уравнение сделать проще: 2a 2 = 4(r) 2 ;
делим уравнение на 2: (a 2 ) = 2(r) 2 ;
извлекаем корень: a = √(2r).

В итоге получаем последнюю формулу: а (сторона квадрата) = √(2r).

Найденная сторона квадрата умножается на 4, далее применяется стандартная формула по нахождению периметра: P = 4√(2r).

Задача:

Дан квадрат, который вписан в окружность, ее радиус равен 5. Значит, диагональ квадрата равняется 10. Применяем теорему Пифагора: 2(a 2 ) = 10 2 , то есть 2a 2 = 100. Делим полученное на два и в результате: a 2 = 50. Так как это не табличное значение, используем калькулятор: а = √50 = 7,07. Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!

Рассмотрим еще один вопрос

Часто в задачах встречается другое условие: как найти площадь квадрата, если известен периметр?

Мы уже рассмотрели все необходимые формулы, поэтому для решения задач подобного типа, необходимо умело их применять и связывать между собой. Перейдем сразу к наглядному примеру: Площадь квадрата равна 25 см 2 , найдите его периметр.

Шаги решения:

Находим сторону квадрата: а = √25 = 5.

Находим сам периметр: Р = 4*а = 4*5 = 20.

Подводя итог, важно напомнить, что такие легкие формулы применимы не только в учебной деятельности, но и повседневной жизни. Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Площадь прямоугольника, как не будет дерзко звучать, но это важное понятие. В повседневной жизни мы постоянно сталкиваемся с ним. Узнать размер полей, огородов, рассчитать количество краски, необходимой для побелки потолка, сколько понадобится обоев для оклейки ко

мнаты и другое.

Геометрическая фигура

Для начала поговорим о прямоугольнике. Это фигура на плоскости, которая имеет четыре прямых угла, а ее противоположные стороны равны. Стороны его привыкли называть длиной и шириной. Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.

Площадь=длина*ширина

Но еще одна оговорка: длина и ширина должны быть выражены в одинаковых единицах измерения, то есть метр и метр, а не метр и сантиметр. Записывается площадь латинской буквой S. Для удобства обозначим длину латинской буквой b, а ширину латинской буквой a, как показано на рисунке. Отсюда мы делаем вывод, что единицей измерения площади является мм 2 , см 2 , м 2 и т. д.

Рассмотрим на конкретном примере, как найти площадь прямоугольника. Длина b=10 ед. Ширина a=6 ед. Решение: S=a*b, S=10 ед.*6 ед., S=60 ед 2 . Задача. Как узнать площадь прямоугольника, если длина в 2 раза больше ширины и составляет 18 м? Решение: если b=18 м, тогда а=b/2, a=9 м. Как найти площадь прямоугольника, если известны обе стороны? Правильно, подставить в формулу. S=a*b, S=18*9, S=162 м 2 . Ответ: 162 м 2 . Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.

Площади противоположных сторон равны. Вычислим площадь стены с размерами 5,5 м и 3 м. S стены 1 =5,5*3,

S стены 1 =16,5 м 2 . Следовательно, противоположная стена имеет площадь равную 16,5 м 2 . Найдем площади следующих двух стен. Стороны их, соответственно, равны 3,5 м и 3 м. S стены 2 =3,5*3, S стены 2 =10,5 м 2 . Значит, и противоположная сторона равна 10,5 м 2 . Сложим все результаты. 16,5+16,5+10,5+10,5=54 м 2 . Как вычислить площадь прямоугольника, если стороны выражены в разных единицах измерения. Ранее мы вычисляли площади в м 2 , то и в этом случае будем использовать метры. Тогда ширина рулона обоев будет равна 0,5 м. S рулона =10*0,5, S рулона =5 м 2 . Теперь узнаем, сколько рулонов необходимо для оклейки комнаты. 54:5=10,8 (рулонов). Так как они измеряются целыми числами, то нужно купить 11 рулонов обоев. Ответ: 11 рулонов обоев. Задача. Как вычислить площадь прямоугольника, если известно, что ширина на 3 см короче длины, а сумма сторон прямоугольника составляет 14 см? Решение: пусть длина х см, тогда ширина (х-3) см. х+(х-3)+х+(х-3)=14, 4х-6=14, 4х=20, х=5 см — длина прямоугольника, 5-3=2 см — ширина прямоугольника, S=5*2, S=10 см 2 Ответ: 10 см 2 .

Резюме

Рассмотрев примеры, надеюсь, стало понятно, как найти площадь прямоугольника. Напомню, что единицы измерения длины и ширины должны совпадать, иначе получится неправильный результат, чтобы не допустить ошибок, читайте задание внимательно. Иногда сторона может быть выражена через другую сторону, не стоит бояться. Обратитесь к нашим решенным задачам, вполне возможно, они могут помочь. Но хоть раз в жизни мы сталкиваемся с нахождением площади прямоугольника.

Что такое площадь и что такое прямоугольник

Площадь – это такая геометрическая величина, с помощью которой можно определить размер какой-либо поверхности геометрической фигуры.

На протяжении многих веков так повелось, что вычисление площади называли квадратурой. То есть, чтобы узнать площадь несложных геометрических фигур, достаточно было подсчитать количество единичных квадратов, которыми условно были покрыты фигуры. А фигуру, которая имела площадь, называли квадрируемой.

Поэтому, можно подвести итог, что площадь – это такая величина, которая показывает нам размер части плоскости, соединенной между собой отрезками.

Прямоугольник – это такой четырехугольник, у которого все углы прямые. То есть, четырехстороннюю фигуру, которая имеет четыре прямых угла и ее противоположные стороны равны, называют прямоугольником.

Как найти площадь прямоугольника

Самый простой способ нахождения площади прямоугольника – взять прозрачную бумагу, например кальку, или клеенку и расчертить ее на равные квадратики по 1 см, а потом приложить к изображению прямоугольника. Количество заполненных квадратиков и будет площадью в сантиметрах квадратных. Например, на рисунке видно, что прямоугольник попадает в 12 квадратов, значит, его площадь равна – 12 кв. см.

Но для нахождения площади больших объектов, например квартиры, необходим более универсальный способ, поэтому была доказана формула, чтобы найди площадь прямоугольника необходимо умножить его длину на ширину.

А теперь давайте попробуем записать правило нахождения площади прямоугольника в виде формулы. Обозначим площадь нашей фигуры буквой S, буква а – будет обозначать его длину, а буква b – ширину.

В итоге получаем вот такую формулу:

S = а * b.

Если наложить эту формулу на рисунок прямоугольника выше, то мы получим те же 12 кв.см, т.к. а = 4 см, b = 3 см, а S = 4 * 3 = 12 кв.см.

Если взять две идентичные фигуры, и наложить их одну на другую, то они совпадут, а будут называться равными. У таких равных фигур будут также равны их площади и периметры.

Зачем уметь находить площадь

Во-первых, если вы знаете, как найти площадь какой-либо фигуры, то с помощью ее формулы вы без проблем сможете решать любые задачи по геометрии и тригонометрии.
Во-вторых, научившись находить площадь прямоугольника, вы сначала сможете решать простые задачки, а со временем перейдете к решению более сложных, и научитесь находить площади фигур, которые вписаны в прямоугольник или около него.
В-третьих, зная такую простую формулу, как S = а * b, вы получаете возможность без проблем решать любые простые бытовые задачи (например, находить S квартиры или дома), а со временем и сможете применить их к решению сложных архитектурных проектов.

То есть, если совсем упростить формулу нахождения площади, то она будет выглядеть так:

П = Д х Ш,

Что обозначает П – это искомая площадь, Д – это ее длина, Ш – обозначает ее ширину, а х – является знаком умножения.

А известно ли вам, что площадь любого многоугольника можно условно разбить на определенное количество квадратных блоков, которые находятся внутри этого многоугольника? Какая разница между площадью и периметром

Давайте на примере попробуем понять разницу между периметром и площадью. Например, наша школа находится на участке, который огражден забором – суммарная длина этого забора будет периметром, а то пространство, которое находится внутри ограждения и является площадью.

Единицы измерения площади

Если периметр одномерный измеряется в линейных единицах, которыми являются дюймы, футы и метры, то S относится к двумерным исчислениям и имеет свою длину и ширину.

И измеряется S в квадратных единицах, таких, как:

Один квадратный миллиметр, где S квадрата имеет сторону, равную одному миллиметру;
Квадратный сантиметр, имеет S такого квадрата, у которого сторона равна одному сантиметру;
Квадратный дециметр равен S этого квадрата со стороной в один дециметр;
Квадратный метр имеет S квадрата, сторона которого равна одному метру;
И наконец, квадратный километр имеет S квадрата, сторона которого равна одному километру.

Для измерения площадей больших участков на поверхности Земли используют такие единицы, как:

Один ар или сотка – если S квадрата имеет сторону десять метров;
Один гектар равен S квадрата, у которого сторона имеет сто метров.

Задачи и упражнения

А теперь давайте рассмотрим несколько примеров.

На рисунке 62 нарисована фигура, которая имеет восемь квадратов и каждая сторона этих квадратов равна одному сантиметру. Поэтому S такого квадрата будет квадратный сантиметр.

Если записать, то это будет выглядеть так:

1 см2. А S все этой фигуры, состоящей из восьми квадратов, будет равняться 8 кв.см.

Если взять какую-нибудь фигуру и разбить ее на «р» квадратов со стороной, равной одному сантиметру, то ее площадь будет равна:

Р см2.

Давайте рассмотрим прямоугольник, изображений на рисунке 63. Этот прямоугольник состоит из трех полос, а каждая такая полоска разбита на пять равных квадратов, имеющих сторону в 1 см.

Попробуем найти его площадь. И так берем пять квадратов, и умножаем на три полоски и получаем площадь равную 15 кв.см.:

Рассмотрим следующий пример. На рисунке 64 изображен прямоугольник ABCD, ломаной линией KLMN он разбит на две части. Первая его часть равна площади 12 см2, а вторая имеет площадь 9 см2. Теперь давайте найдем площадь всего прямоугольника:

Итак, берем три и умножаем на семь и получаем 21 кв.см:

3 7 = 21 кв.см. При этом 21 = 12 + 9.

И приходим к выводу, что площадь всей нашей фигуры равна сумме площадей ее отдельных частей.

Рассмотрим еще один пример. И так на рисунке 65 изображен прямоугольник, который с помощью отрезка АС разбит на два равных треугольника ABC и ADC

А так, как нам уже известно, что квадрат – это такой же прямоугольник, только имеющий равные стороны, то площадь каждого треугольника будет равняться половине площади всего прямоугольника.

Представим, что сторона квадрата равна а, то:

S = a a = a2.

Делаем вывод, что формула площади квадрата будет иметь такой вид:

А запись a2 называется квадратом числа а.

И так, если сторона нашего квадрата равна четырем сантиметрам, то его площадь будет:

4 4, то есть 4 * 2 = 16 кв.см.

Вопросы и задания

Найдите площадь фигуры, которая разбита на шестнадцать квадратов, сторона которых равна одному сантиметру.
Вспомните формулу прямоугольника и запишите ее.
Какие измерения нужно произвести, чтобы узнать площадь прямоугольника?
Дайте определение равным фигурам.
Могут ли иметь равные фигуры различные площади? А периметры?
Если вам известны площади отдельных частей фигуры, как узнать ее общую площадь?
Сформулируйте и запишите, чему равняется площадь квадрата.

Историческая справка

А известно ли вам, что древние люди в Вавилоне умели рассчитать площадь прямоугольника. Так же древние египтяне делали расчеты различных фигур, но так как точных формул они не знали, то вычисления имели небольшие погрешности.

В своей книге «Начала» знаменитый древнегреческий математик Евклид, описывает различные способы вычисления площадей разных геометрических фигур.

Вычисление формулы объема и площади в Excel

Программа Excel является лучшим калькулятором. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы. Все их возможности поддерживает программа Excel. Более того, он имеет неоспоримые преимущества.

В некоторых формулах можно выполнить только одно математическое вычисление при калькуляционных расчетах. В таких случаях, если меняются данные нужно изменить формулу. Но если все данные будут распределены по ячейкам, а формула будет только ссылаться на них, то при любых изменениях нет необходимости менять формулу. Одна формула может использоваться многократно. Чтобы понять, как это работает, лучше привести несколько практических примеров.

Как рассчитать объем и площадь в Excel

В ячейке A1 запишем формулу вычисления объема параллелепипеда: a = 6 см; b = 8 см; c = 12 см.

В ячейке A2 запишем формулу вычисления площади круга: r = 25 см.

В ячейке A3 формула содержит безаргументную функцию ПИ(), которая содержит в себе полное число ПИ (а не 3.3 (A2 – это ссылка на ячейку).

В ячейке A2 будем вводить разные радиусы и после каждого ввода в ячейке B2 будем получать результат вычисления объема сфер соответствующих своим радиусам.

Примечание. Если вы используете в Excel многократные вычисления или формулы содержащие ссылки на ячейки в качестве переменных значений, то всегда подписывайте каждую ячейку с входящими данными и формулами. Это позволит избежать ошибок и легко читать значения или результаты вычисления формул.

Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма. Площади плоских фигур. Формулы площади.

Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма.

Справочно: число пи

Пример 1

Прямоугольный поднос имеет длину 900 мм и ширину 350 мм. Определить его площадь в а) мм², б) в см², в) в м²

Решение:

а) Площадь =длина*ширина=900*350=315000 мм²

б) 1 см²=100 мм², следовательно,

315000 мм²=315000/100=3150 см²

1 м²=10000 см², следовательно,

3150 см²=3150/10000=0.315 м²

Пример 2

Определить площадь поперечного сечения балки, изображенной на рисунке.

Сечение балки можно разделить на три отдельных прямоугольника, как показано на рисунке

Sa=3*50=150 мм²

Sb=(65-5-3)*4=228 мм²

Sc=60*5=300 мм²

Общая площадь балки 150+228+300=678 мм²=6.78 см².

Пример 3

Определить площадь дорожки, показанной на рисунке.

Решение:

Площадь дорожки = площадь большого прямоугольника — площадь малого прямоугольника

S=35*15-29*11=206 м²

Пример 4

Определить площадь параллелограмма, показанного на рисунке (размеры приведены в миллиметрах).

Площадь параллелограмма = основание * высота. Высота h определяется по теореме Пифагора BC²=CE²+h²

Тогда

20²=(36-30)²+h²

h²=20²-6²=164

h=14,3 (приблизительно)

Следовательно, S_abcd=30*14.3=429 мм²

Пример 5

Показана боковая сторона здания. Определить площадь кирпичной кладки на боковой стороне.

Боковая сторона состоит из прямоугольника и треугольника.

S_прям.=6*10=60 м²

S_треуг.=1/2*основание*высота

CD=5 м, AD=6 м, следовательно, AC=3 м (по т. Пифагора). Следовательно,

S_треуг.=1/2*10*3=15 м².

Общая площадь кирпичной кладки есть 60+15=75 м²

Пример 6

Определить площади кругов, имеющих а) радиус 3 см, б) диаметр 10 мм, в) длину окружности 60 мм.

S=πr² или πd²/4.

а) S=πr²=π(3)²=9π=28.26 см²

б) S=πd²/4=π(10)²/4=100π/4=78.5 мм²

в) Длина окружности с=2πr, следовательно,

r=c/2π=60/2π=30/π

S=πr²=π(30/π)²=286.62 мм²

Пример 7

Вычислить площадь правильного восьмиугольника со стороной 5 см и поперечником 10 см.

Восьмиугольник — это многоугольник с 8 сторонами. Если из центра многоугольника провести лучи к вершинам, получится восемь одинаковых треугольников.

S_треуг.=1/2*основание*высота=1/2*5*10/2=12.5 см²

Площадь восьмиугольника есть 8*12.5=100 см²

Пример 8

Определить площадь правильного шестиугольника со стороной 10 см.

Шестиугольник — это многоугольник с шестью сторонами, который может быть разбит на шесть равных треугольников, как показано на рис. сходящиеся в центре многоугольника углы треугольника равны 360^о/6=60^о

Другие два угла каждого треугольника составляют в сумме 120^о и равны между собой.

Следовательно, все треугольники являются равносторонними с углами 60^о и стороной 10 см

S_треуг.=1/2*основание*высота

Высоту h находим по теореме Пифагора:

10²=h²+5²

Отсюда h²=100-25=75

h=8.66 см

Следовательно, S_треуг.=1/2*10*8.66=43.3 см ²

Площадь шестиугольника равна 6*43.3=259.8 см²

Площадь прямоугольников — объяснение и примеры

По определению, площадь прямоугольника — это область, охватываемая прямоугольником в двухмерной плоскости . Прямоугольник — это двумерный многоугольник с четырьмя сторонами, четырьмя углами и четырьмя вершинами.

Прямоугольник состоит из двух сторон: длины (L) и ширины (W). Длина прямоугольника — самая длинная сторона, а ширина — самая короткая. Ширина прямоугольника иногда обозначается как ширина (b).

Как найти площадь прямоугольника?

Площадь прямоугольника можно рассчитать, подсчитав количество маленьких полных квадратов размером 1 * 1 кв. Единиц, необходимых для покрытия прямоугольника.

Например, если количество подсчитанных полных квадратов равно 20, это означает, что площадь прямоугольника равна 20 единицам квадратов.

Недостатком этого метода является то, что он не дает точных значений площади, а также метод неприменим для определения площади больших плоскостей.

Площадь прямоугольника Формула

Площадь прямоугольника равна произведению ширины и длины прямоугольника.

Следовательно, формула площади прямоугольника утверждает, что:

Площадь прямоугольника = Длина x Ширина

A = L * W, где A — площадь, L — длина, W — ширина или ширина. .

ПРИМЕЧАНИЕ: При умножении длины на ширину всегда проверяйте, что вы работаете в одной и той же единице длины. Если они даны в разных единицах, замените их на одну и ту же единицу.

Давайте решим несколько примеров задач о площади прямоугольника.

Пример 1

Найдите площадь прямоугольника, если его длина 25 м, а ширина 10 м.

Решение

A = l x w

Заменить 25 на l и 10 на w.

= (25 x 10) м ²

= 250 м ²

Итак, площадь прямоугольника 250 м ².

Пример 2

Найдите площадь прямоугольника, длина и ширина которого составляют 10 см и 3 см соответственно.

Раствор

Дано,
Длина (l) = 10 см.
Ширина (б) = 3 см.
Площадь прямоугольника = длина × ширина

= 10 × 3 см ².

= 30 см ².

Пример 3

Если периметр прямоугольника составляет 60 см, а его длина в 5 раз больше ширины, найдите площадь прямоугольника.

Решение

Пусть ширина будет x.

Длина в 5 раз больше ширины, длина = 5x.

Но периметр прямоугольника = 2 (l + w) = 60 см

Замените 5x вместо l и x вместо w.

60 = 2 (5x + x)

60 = 12x

Разделите обе стороны на 12, чтобы получить.

x = 5

Теперь подставьте x = 5 в уравнение длины и ширины.

Следовательно, ширина = 5 см, а длина = 25 см.

Но площадь прямоугольника = lxw

= (25 x 5) см ²

= 125 см ²

Пример 4

Найдите площадь прямоугольника длиной 12 см и диагональ 13 см.

Решение

Здесь ширина не указана, поэтому мы используем теорему Пифагора для определения ширины.

c ² = a ² + b ²

13 ² = a ² + 12 ²

169 = a ² + 144.

Вычесть 144 с обеих сторон .

169 — 144 = a ² + 144 — 144

25 = a ²

Найдя квадратный корень из обеих сторон, мы получим.

a = 5

Следовательно, ширина прямоугольника 5 см.

Теперь посчитаем площадь.

A = Д x Ш

= (12 x 5) см ²

Пример 5

Если цена цементирования пола составляет 12,40 долларов США за квадратный метр, найдите стоимость цементирования прямоугольного пола длиной 20 м и шириной 10 м.

Раствор

Чтобы найти общую стоимость цементирования пола, умножьте площадь пола на норму цементирования.

Площадь = Д x Ш

= (20 x 10) м ²

= 200 м ²

Стоимость цементирования = площадь x скорость цементирования

= 200 м ² x 12,40 долл. США / м ²

= 2480 долларов США

Пример 6

Длина и ширина находятся в соотношении 11: 7, а его площадь составляет 693 квадратных фута. Найдите его длину и ширину.

Решение

Пусть общее соотношение длины и ширины = x

Следовательно, длина = 11x

Ширина = 7x

Площадь прямоугольника = L x W

693 кв.футов = (11x) (7x)

693 кв. ft = 77x ²

Разделим обе стороны на 77.

x ² = 9

Найдите квадрат обеих сторон, чтобы получить;

x = 3.

Заменитель.

Длина = 11x = 11 * 3 = 33

Ширина = 7x = 7 * 3 = 21

Следовательно, длина прямоугольника составляет 33 фута, а его ширина — 21 фут.

Пример 7

Длина прямоугольника 0,7 м, ширина 50 см.Какова площадь прямоугольника в метрах?

Решение

Длина = 0,7 м

Ширина = 50 см.

Преобразуйте 50 см в метры, разделив 50 на 100. Итак, 50 см = 0,5 м

Площадь = Д x Ш

= (0,7 x 0,5) м ²

= 0,35 м ²

Пример 8

Размер прямоугольной стены 75 м на 32 м. Узнайте стоимость покраски стены, если ставка покраски 5 рупий за кв.м.

Решение

Площадь = Д x Ш

= (75 x 32) м ²

= 2400 м ²

Чтобы получить стоимость покраски стены, умножаем площадь стены по скорости покраски.

Стоимость = 2400 м ² x 5 рупий за кв.м

= 12000 рупий

Пример 9

Пол прямоугольного двора, размером 50 м на 40 м, покрыт прямоугольной плиткой размеры, 1 м на 2 м.Найдите общее количество плиток, необходимых для полного покрытия пола двора.

Решение

Сначала вычислите площадь пола двора и плитки.

Площадь пола двора = (50 x 40) м ²

= 2000 м ²

Площадь плитки = (1 x 2) м ²

= 2 м ²

Чтобы найти количество плиток, необходимое для покрытия пола двора, мы делим пол двора на площадь плитки.

Количество плиток = 2000 м ²/2 м ²

= 1000

Следовательно, для покрытия пола необходимо 1000 плиток.

Предыдущий урок | Главная страница | Следующий урок

Расчетная площадь | SkillsYouNeed

Площадь — это мера того, сколько места внутри фигуры. Расчет площади формы или поверхности может быть полезен в повседневной жизни — например, вам может потребоваться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы засеять лужайку.

На этой странице описаны основные сведения, которые необходимо знать для понимания и расчета площадей общих форм, включая квадраты и прямоугольники, треугольники и круги.

Расчет площади по сетке

Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.

В этом примере внутри прямоугольника 10 квадратов сетки.

Чтобы найти значение площади с помощью метода сетки, нам нужно знать размер, который представляет квадрат сетки.

В этом примере используются сантиметры, но тот же метод применяется к любой единице длины или расстояния. Например, вы можете использовать дюймы, метры, мили, футы и т. Д.

В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному квадратному сантиметру.

Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.

Есть 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.

В математике мы сокращаем «квадратные сантиметры» до ². ² означает «в квадрате».

Каждый квадрат сетки равен 1 см ².

Площадь большого квадрата 16см ².

Подсчет квадратов на сетке для определения площади работает для всех форм — если известны размеры сетки. Однако этот метод становится более сложным, когда формы не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.

В этом примере квадрат не точно помещается на сетке.

Мы все еще можем вычислить площадь, считая квадраты сетки.

Имеется 25 полных квадратов сетки (заштрихованы синим цветом).
10 квадратов полусетки (заштрихованы желтым цветом) — 10 полуквадратов равны 5 полным квадратам.
Также есть 1 четверть квадрата (заштрихована зеленым) — (или 0,25 целого квадрата).
Сложите целые квадраты и дроби вместе: 25 + 5 + 0.25 = 30,25.

Следовательно, площадь этого квадрата составляет 30,25 см ².

Вы также можете записать это как 30¼см ².

Хотя использование сетки и подсчета квадратов внутри фигуры — очень простой способ изучения концепции площади, он менее полезен для нахождения точных областей с более сложными формами, когда можно сложить много частей квадратов сетки.

Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.

Остальная часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сеток.

Площади простых четырехугольников:

Квадраты, прямоугольники и параллелограммы

Простейшие (и наиболее часто используемые) вычисления площади выполняются для квадратов и прямоугольников.

Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.

Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это на себя, чтобы найти площадь.Это то же самое, что сказать длину ² или длину в квадрате.

Рекомендуется проверять, является ли фигура квадратом, измеряя две стороны. Например, стена комнаты может выглядеть как квадрат, но когда вы ее измеряете, вы обнаруживаете, что на самом деле это прямоугольник.

Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.

Типовой план помещения не может состоять из простого прямоугольника или квадрата:

В этом и других подобных примерах фокус состоит в том, чтобы разделить фигуру на несколько прямоугольников (или квадратов).Неважно, как вы разделите фигуру — любое из трех решений даст один и тот же ответ.

Для решений 1 и 2 необходимо создать две фигуры и сложить их площади, чтобы найти общую площадь.

Для решения 3 вы создаете большую форму (A) и вычитаете из нее меньшую форму (B), чтобы найти площадь.

Другая распространенная проблема — найти область границы — фигуру внутри другой фигуры.

В этом примере показана дорожка вокруг поля — ширина дорожки 2 метра.

Опять же, в этом примере есть несколько способов определить площадь пути.

Вы можете просмотреть путь как четыре отдельных прямоугольника, вычислить их размеры, а затем их площадь и, наконец, сложить области, чтобы получить итог.

Более быстрый способ — вычислить площадь всей формы и площадь внутреннего прямоугольника. Вычтите площадь внутреннего прямоугольника из всей, оставив площадь пути.

Площадь всей формы составляет 16 м × 10 м = 160 м ².
Мы можем определить размеры средней секции, потому что знаем, что путь по краю имеет ширину 2 метра.
Ширина всей формы составляет 16 м, а ширина пути по всей форме — 4 м (2 м слева от формы и 2 м справа). 16 м — 4 м = 12 м
То же самое для высоты: 10м — 2м — 2м = 6м
Итак, мы вычислили, что средний прямоугольник имеет размер 12 × 6 м.
Таким образом, площадь среднего прямоугольника составляет: 12 м × 6 м = 72 м ².
Наконец, мы убираем область среднего прямоугольника из области всей формы. 160 — 72 = 88м ².

Площадь тропы 88м ².

Параллелограмм — это четырехгранная форма с двумя парами сторон равной длины — по определению прямоугольник является разновидностью параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехсторонних фигурах с наклонными линиями, как показано здесь.

Площадь параллелограмма рассчитывается так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных (или отклоненных от вертикали) сторон, а расстояние между сторонами.

Из диаграммы вы можете видеть, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.

Представьте себе воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.

Области треугольников

Может быть полезно думать о треугольнике как о половине квадрата или параллелограмма.

Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро вычислить его площадь.

Площадь треугольника (высота × ширина) ÷ 2.

Другими словами, вы можете вычислить площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите свой ответ на 2.

Высота треугольника измеряется по прямой линии от нижней линии (основания) до «вершины» (верхней точки) треугольника.

Вот несколько примеров:

Площадь трех треугольников на диаграмме выше одинакова.

Каждый треугольник имеет ширину и высоту 3 см.

Площадь рассчитана:

(высота × ширина) ÷ 2

3 × 3 = 9

9 ÷ 2 = 4,5

Площадь каждого треугольника составляет 4,5 см ².

В реальных ситуациях вы можете столкнуться с проблемой, требующей найти площадь треугольника, например:

Вы хотите покрасить фронтальный конец сарая. Вам нужно посетить магазин украшений только один раз, чтобы получить нужное количество краски.Вы знаете, что литр краски покроет 10 м ² стены. Сколько краски нужно, чтобы покрыть фронтон?

Вам нужно три измерения:

A — Общая высота до вершины крыши.

B — Высота вертикальных стен.

C — Ширина здания.

В этом примере измерения:

A — 12,4 м

B — 6,6 м

C — 11,6 м

Следующий этап требует дополнительных расчетов.Подумайте о здании как о двух формах: прямоугольнике и треугольнике. По имеющимся у вас измерениям вы можете рассчитать дополнительное измерение, необходимое для определения площади фронтона.

Размер D = 12,4 — 6,6

D = 5,8 м

Теперь вы можете определить площадь двух частей стены:

Площадь прямоугольной части стены: 6,6 × 11,6 = 76,56 м ²

Площадь треугольной части стены: (5.8 × 11,6) ÷ 2 = 33,64 м ²

Сложите эти две области вместе, чтобы получить общую площадь:

76,56 + 33,64 = 110,2 м ²

Как вы знаете, один литр краски покрывает 10 м ² стены, поэтому мы можем рассчитать, сколько литров нам нужно купить:

110,2 ÷ 10 = 11,02 л.

На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых канистрах, результат — чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но, если мы не будем разбавлять краску водой, этого будет недостаточно.Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать потерь и оставит большую часть литра для подкраски позднее. И не забывайте, что если вам нужно нанести более одного слоя краски, вы должны умножить количество краски для одного слоя на количество необходимых слоев!

Области кругов

Чтобы вычислить площадь круга, вам необходимо знать его диаметр или радиус .

Диаметр круга — это длина прямой линии от одной стороны круга до другой, проходящей через центральную точку круга. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)

Радиус круга — это длина прямой линии от центральной точки круга до его края. Радиус составляет половину диаметра. (радиус = диаметр ÷ 2)

Вы можете измерить диаметр или радиус в любой точке окружности — важно измерять, используя прямую линию, проходящую через (диаметр) или заканчивающуюся в (радиусе) центром окружности.

На практике при измерении окружностей часто легче измерить диаметр, а затем разделить на 2, чтобы найти радиус.

Радиус нужен для вычисления площади круга, формула:

площадь круга = πR ².

Это означает:

π = Pi — постоянная, равная 3,142.

R = радиус окружности.

R ² (радиус в квадрате) означает радиус × радиус.

Следовательно, круг с радиусом 5 см имеет площадь:

3.142 × 5 × 5 = 78,55 см ².

Круг диаметром 3 м имеет площадь:

Сначала прорабатываем радиус (3м ÷ 2 = 1,5м)

Затем примените формулу:

πR ²

3,142 × 1,5 × 1,5 = 7,0695.

Площадь круга диаметром 3 м составляет 7,0695 м ².

Последний пример

В этом примере используется большая часть содержимого этой страницы для решения простых задач с областями.

Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (номер записи: 376599).

Этот пример включает поиск области фасада дома, деревянной решетчатой части — исключая дверь и окна. Вам нужны следующие размеры:

A — 9,7 м	B — 7,6 м
C — 8,8 м	D — 4,5 м
E — 2.3 мес.	F — 2,7 м
G — 1,2 м	H — 1,0 м

Примечания:

Все размеры являются приблизительными.
Не нужно беспокоиться о границе вокруг дома — она не учтена в измерениях.
Мы предполагаем, что все прямоугольные окна одинакового размера.
Размер круглого окна — это диаметр окна.
Размер двери включает ступеньки.

Какова площадь деревянной реечной части дома?

Работы и ответы ниже:

Ответы на приведенный выше пример

Сначала определите площадь основной формы дома — прямоугольника и треугольника, составляющих форму.

Главный прямоугольник (B × C) 7,6 × 8,8 = 66,88 м ².

Высота треугольника (A — B) 9,7 — 7,6 = 2,1.

Следовательно, площадь треугольника равна (2.1 × C) ÷ 2.
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м ².

Общая площадь фасада дома равна сумме площадей прямоугольника и треугольника:

66,88 + 9,24 = 76,12 м ².

Затем проработайте площади окон и дверей, чтобы их можно было вычесть из всей площади.

Площадь двери и ступеней составляет (Д × В) 4,5 × 2,3 = 10,35 м ².

Площадь одного прямоугольного окна составляет (G × F) 1.2 × 2,7 = 3,24 м ².

Есть пять прямоугольных окон. Умножьте площадь одного окна на 5.

3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).

Круглое окно имеет диаметр 1 м, поэтому радиус 0,5 м.

Используя πR ², определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855м ².

Затем сложите площади двери и окон.

(зона двери) 10,35 + (прямоугольная зона окон) 16.2 + (площадь круглого окна) 0,7855 = 27,3355

Наконец, вычтите общую площадь окон и дверей из всей площади.

76,12 — 27,3355 = 48,7845

Площадь деревянного реечного фасада дома и ответ на проблему: 48,7845м ².

Вы можете округлить ответ до 48,8 м ² или 49 м ².

См. Нашу страницу Оценка, приближение и округление .

Как найти площадь прямоугольника (формула и видео) // Репетиторы.com

Содержание

Что такое прямоугольник?
Площадь прямоугольника
Формула площади прямоугольника
Как найти площадь прямоугольника
Как рассчитать площадь прямоугольника
Примеры площади прямоугольника

Что такое прямоугольник?

Прежде чем найти площадь прямоугольника, убедитесь, что у вас на самом деле прямоугольник . По определению, прямоугольник представляет собой четырехстороннюю форму, все углы которой равны прямым углам, составляющим 90 градусов.

Вы можете распознать прямоугольник, проверив его два идентифицирующих свойства :

Четыре внутренних прямых угла
Две пары параллельных совпадающих сторон

Единственный способ построить многоугольник, удовлетворяющий этим двум требованиям, — это создать прямоугольник. Поэтому проверьте, есть ли у вас плоская замкнутая четырехгранная форма (это плоская фигура, четырехугольник с внутренней и внешней стороной). Если все в порядке, посмотрите, есть ли у него четыре внутренних угла по 90 ° каждый с противоположными параллельными конгруэнтными сторонами.

Если ваша форма обладает всеми этими качествами, у вас есть прямоугольник, и вы можете определить его площадь.

Площадь прямоугольника

Площадь — это количество плоского пространства внутри прямоугольника или замкнутой формы. Он всегда выражается в квадратных единицах линейного измерения. Итак, если фигура имеет длину 11 ярдов и ширину 7 ярдов, ее площадь выражается в квадратных ярдах, даже если форма не является квадратом.

Площадь никогда не бывает линейной мерой.

Квадратная единица чего-либо — это одна единица длины, умноженная на одну единицу ширины.Вот некоторые общие линейные единицы измерения, их квадратные единицы, а также способы их записи и сокращения:

дюймов (дюймов) = квадратные дюймы, квадратные дюймы, 2 дюйма
футов (футы) = квадратные футы, кв. Футы, фут2
миллиметров (мм) = квадрат, мм, мм2
сантиметров (см) = квадрат см, см2
метров (м) = квадратных метров, м2

Каждый раз вы просто берете единицу линейной меры и умножаете ее на себя (возводите в квадрат). Вы делаете это, потому что пытаетесь понять, сколько замкнутого пространства содержит фигура.

Формула площади прямоугольника

Формула для площади прямоугольника:

площадь = длина × ширина

Однако, если вы не знаете, какова длина прямоугольника, эта формула не принесет вам много пользы. Поэтому убедитесь, что вы можете идентифицировать два линейных измерения прямоугольника.

Под длиной любого многоугольника всегда понимается его большее измерение, даже если его длина не представлена по горизонтали.

Как найти площадь прямоугольника

Представьте, что вы устанавливаете новый ковер от стены до стены в комнате.Это очень распространенное использование для поиска области. Комната имеет длину 4 метра и ширину 3 метра. Чтобы достичь всех четырех углов (от стены до стены), ваш ковер также должен быть 4 метра в длину и 3 метра в ширину.

Уравнение площади прямоугольника

площадь = длина × ширина

Площадь пола и коврового покрытия:

площадь = 4м × 3м

площадь = 12м2

Как вычислить площадь прямоугольника

Следующий пример — чрезвычайно распространенное практическое использование для определения площади прямоугольников.Допустим, вы перекрашиваете стены своей спальни. Не обращая внимания на места для окон, дверей шкафа и двери спальни (в любом случае вы всегда покупаете немного больше краски, чем вам нужно!), Вот размеры стены:

Северная стена: 8 футов в высоту и 9 футов в ширину

Восточная стена: 8 футов в высоту и 12 футов в ширину

Южная стена: 8 футов в высоту и 9 футов в ширину

Западная стена: 8 футов в высоту и 12 футов в ширину

Обратите внимание, что все стены одинаковой высоты. Также обратите внимание, что северная и южная стены имеют одинаковую ширину, а восточная и западная стены имеют одинаковую ширину.Вы знаете, что ваша спальня представляет собой прямоугольник. Теперь посчитаем площадь:

Северная стена: 8 футов × 9 футов = 72 фут2

Восточная стена: 8 футов × 12 футов = 96 футов2

Южная стена: 8 футов × 9 футов = 72 кв. Фута

Западная стена: 8 футов × 12 футов = 96 футов2

Вы можете быстро сложить их, чтобы определить, что вашей комнате требуется 336 квадратных футов покрытия краски. Типичный галлон краски покрывает 400 квадратных футов, поэтому вам понадобится один галлон краски.

Как рассчитать площадь прямоугольника

Предположим, вам нужно мягкое одеяло для дневной будки вашей собаки.Пол питомника имеет размеры 54 дюйма в длину и 36 дюймов в ширину. Какой площади одеяла вам нужно?

площадь = длина × ширина

площадь = 54 «× 36»

площадь = 1944 кв. Дюйм

Примеры площади прямоугольника

Пример # 2

Допустим, вам нужен новый приветственный коврик для входа в дом. Вы видите один размером 75 сантиметров (см) в длину и 40 см в ширину. Какова площадь дверного коврика?

площадь = длина × ширина

площадь = 75 см × 40 см

площадь = 3000 см2

Пример # 3

Площадь часто связана с ценообразованием.Ковер продается квадратными или квадратными метрами. Плитка для пола продается квадратными футами. Даже такие вещи, как строительство нового здания и аренда, рассчитываются как затраты на квадратный фут или квадратный метр.

Знание того, как найти площадь прямоугольника, может помочь вам найти выгодные покупки и не тратить деньги зря. Давай попробуем вот такой. У вас есть два коврика:

Синий коврик: 6 футов на 9 футов за 162 доллара США
Коричневый коврик: 9 x 12 футов за 243 доллара

Что дает вам меньшую стоимость квадратного фута? Сначала посчитайте площадь каждого коврика:

площадь = длина × ширина

площадь синего коврика = 6 футов × 9 футов = 54 кв.фута

площадь коричневого ковра = 9 футов × 12 футов = 108 кв.футов

Теперь разделите стоимость каждого ковра на его квадратные футы:

синий ковер = 16254 доллара за фут2 = 3 доллара за фут2

коричневого ковра = 243108 футов2 = 2 доллара.25 фут2

Коричневый коврик дешевле за квадратный фут. Знание того, как найти площадь прямоугольника, помогло вам сэкономить деньги!

Краткое содержание урока

Посмотрев видео и прочитав этот урок, вы узнали, как распознать прямоугольник, какие квадратные единицы связаны с площадью, как рассчитать площадь прямоугольника и как этот навык может быть полезен. Формула для вычисления площади прямоугольника: длина, умноженная на ширину, в квадратных единицах.

Следующий урок:

Что такое квадрат?

Как найти площадь прямоугольника?

Площадь прямоугольника A определяется формулой

A = L W

, где L и W — длина и ширина прямоугольника соответственно.

Как найти площадь прямоугольника? Примеры решений

Пример 1
Найдите площадь прямоугольника длиной 35 метров и шириной 20 метров.
Решение примера 1
Поскольку длина L и ширина W имеют одинаковые единицы, мы применяем приведенную выше формулу, заменяя L и W их значениями следующим образом
A = L W = 35 20 = 700 квадратных метров (или ² м)

Пример 2
Прямоугольное поле имеет длину 360 дюймов и ширину 300 дюймов.Найдите площадь прямоугольника в квадратных футах. (1 фут = 12 дюймов)
Решение примера 2
Поскольку нам нужно найти площадь в квадратных футах, нам нужно преобразовать длину L и ширину W в футы.
L = 360 дюймов = 360/12 = 30 футов
W = 300 дюймов = 300/12 = 25 футов
Площадь прямоугольника A определяется выражением
A = L W = 30 25 = 750 квадратных футов (или ² футов)

Пример 3
Ширина прямоугольника составляет 20 метров, а его длина — пять четвертей его ширины.Найдите площадь этого прямоугольника.
Решение примера 3
Сначала нам нужно найти длину L прямоугольника, учитывая его ширину W = 20 метров.
L = (5/4) W = (5/4) 20 = 5 20/4 = 25 метров
Площадь прямоугольника A определяется выражением
A = L W = 25 20 = 500 квадратных метров (² м)

Пример 4
Длина прямоугольника составляет 1200 метров, а его ширина на 100 метров короче его длины. Найдите площадь этого прямоугольника в квадратных километрах.(1 километр = 1000 метров)
Решение примера 4
Сначала нам нужно найти ширину W прямоугольника, учитывая его длину L = 1200 метров.
W = 1200 — 100 = 1100 метров
Преобразуем длину L и ширину W в километры
L = 1200 метров / 1000 = 1,2 километра
W = 1100 метров / 1000 = 1,1 километра
Площадь прямоугольника A рассчитывается следующим образом
A = L W = 1,2 1,1 = 1,32 квадратных километров (или ² км)

Пример 5
Прямоугольная комната длиной 5 метров и шириной 4.5 метров облицовывают квадратной плиткой по 20 см на каждую сторону. Какое минимальное количество плиток нужно?
Решение примера 5
Нам нужно найти площадь A1 одной плитки в квадратных сантиметрах.
A1 = 20 20 = 400 квадратных сантиметров.
Теперь конвертируем длину L и ширину W комнаты в сантиметры и находим ее площадь A.
L = 5100 = 500 сантиметров
W = 4,5 100 = 450 сантиметров
A = 500 450 = 225 000 квадратных сантиметров
Количество необходимых плиток N определяется делением общей площади комнаты на площадь одной плитки.
N = Общая площадь комнаты / площадь одной плитки = 225000/400 = 562.5 плиток
Количество плиток должно быть целым числом, а также при облицовке комнаты плитками в некоторых местах может потребоваться резка плиток, и поэтому может потребоваться больше плиток. Следовательно, минимальное необходимое количество плиток — 563.

Дополнительные ссылки и ссылки

Площадь, периметр и диагональ прямоугольника — Калькулятор.
Длина и ширина прямоугольника — Калькулятор геометрии.

Площадь прямоугольника — Веб-формулы

Четырехугольник называется прямоугольником, если он параллелограмм и каждый угол составляет 90 градусов.

Прямоугольник — это четырехсторонняя замкнутая фигура. В прямоугольнике все противоположные стороны параллельны и равны. Также в прямоугольнике все смежные стороны перпендикулярны.

Прямоугольник — это четырехугольник, а также параллелограмм.

Рассмотрим прямоугольник с длиной x единиц и шириной y единиц.

Площадь вышеуказанного прямоугольника = Д × Ш

Пример 1: Дан прямоугольник, длина которого равна 5 см, а ширина — 3 см.Найдите площадь этого прямоугольника.

Решение : Чтобы вычислить площадь, мы можем использовать формулу для площади прямоугольника:

A = Д × Ш

Поскольку длина задана как 5 см, мы можем заменить L на 5. Точно так же, поскольку ширина задана как 3 см, мы можем заменить W на 3. После этого мы можем вычислить A , как показано ниже:

A = Д × Ш

A = 3 × 5

А = 15

Теперь вычисленное число 15 имеет значение, только если мы включим для него единицу измерения.Поскольку длина и ширина указаны в см, единицей измерения площади будет ² см. Следовательно:

A = 15 см ²

Пример 2: Найдите площадь сада, длина и ширина сада соответственно 600 м и 400 м.

Решение :

Площадь сада = длина × ширина

A = Д × Ш

А = 600 × 400

A = 240000 м ²

Пример 3: Белая бумага имеет размер 20 см в длину и 15 см в ширину.Джек нарисовал в центре листа прямоугольник 10 см в длину и 5 см в ширину и закрасил весь прямоугольник в фиолетовый цвет. Найдите область фиолетовой части и область белой части.

Решение : Мы знаем, что площадь прямоугольника равна длине × ширине.

Здесь данная бумага имеет форму прямоугольника.

Итак, площадь бумаги = 20см x 15см = 300см² .

А площадь фиолетового прямоугольника = 10см x 5см = 50см² .

Итак, площадь белого участка = 300 см² — 50 см² = 250 см² .

Пример 4: Длина сада прямоугольной формы составляет 250 метров, а ширина сада составляет 175 метров. Найдите площадь прямоугольного сада.

Решение : Длина сада = 250 метров

Ширина сада = 175 метров

Площадь прямоугольного сада = 250 х 175

= 43,750 м ²

Пример 5: В зрительном зале пол покрыт прямоугольным ковром длиной 9 м и шириной 6 м.Вычислите площадь прямоугольного ковра.

Решение :

Учитывая это, длина (L) ковра = 9 м и ширина ковра (W) = 6 м.

Площадь прямоугольника = длина Ширина

Площадь = Д × Ш = 9 × 6 = 54 м ²

Онлайн-калькулятор площади

Прямоугольный калькулятор. Найдите площадь и периметр любого прямоугольника

Если вам нужно знать площадь ковра, участка, экрана телевизора, прямоугольного бассейна или окна, этот прямоугольный калькулятор решит вашу проблему в мгновение ока! Все, что вам нужно сделать, это ввести длину и ширину (или диагональ) и позволить вычислению прямоугольника найти значения P (периметр) и A (площадь).Продолжайте читать, если вы хотите понять, что такое прямоугольник, вас интересуют определение прямоугольника, формулы, свойства прямоугольника … Или вы просто хотите узнать, как найти площадь прямоугольника.

Поскольку вы уже здесь, мы полагаем, что другие наши калькуляторы геометрических фигур могут быть вам интересны. Взгляните на наши замечательные инструменты, поиграйте с ними и опробуйте их!

Прямоугольник — это пример четырехугольника. Может быть, вы хотите посмотреть другие?

Что такое прямоугольник? Определение прямоугольника

Прямоугольник — это четырехугольник с четырьмя прямыми углами .Его также можно определить по-другому: параллелограмм, содержащий прямой угол — если один угол прямой, остальные должны быть такими же. Более того, каждая сторона прямоугольника имеет ту же длину, что и противоположная ему. Он также имеет неравные смежные стороны, в отличие от квадрата, который является частным случаем прямоугольника.

Если вы немного знаете латынь, название фигуры обычно многое объясняет. Слово прямоугольник происходит от латинского rectangulus . Это комбинация rectus (что означает «прямой, прямой») и angulus (угол), поэтому оно может служить простым базовым определением прямоугольника.

Как найти площадь прямоугольника?

На изображении выше показан типичный прямоугольник. У него четыре стороны и четыре прямых угла. Длины его сторон обозначены как a и b , а длина диагонали обозначена как d .

Если все стороны прямоугольника равны, он называется квадратом .

Площадь прямоугольника — это пространство, ограниченное его сторонами, или, другими словами, в пределах периметра прямоугольника.Чтобы найти площадь прямоугольника, все, что вам нужно сделать, это умножить стороны прямоугольника a и b :

Площадь = a * b

Формулы прямоугольника

В нашем калькуляторе прямоугольников реализованы следующие формулы:

Для площади прямоугольника : А = а * б
Для периметра прямоугольника : П = 2 * (а + б)
Для диагонали прямоугольника : d² = a² + b²

Если вас интересует площадь трехмерных тел, а не двумерные формы, воспользуйтесь калькулятором площади поверхности.

Вычисление прямоугольника: найти A (площадь)

Поскольку мы знаем формулу площади прямоугольника A = a * b , давайте на примере покажем, как можно вычислить это свойство:

Выберите длину прямоугольника — например, a = 5 см .
Определитесь с шириной прямоугольника — например, b = 6 см .
Умножьте эти два значения: A = 5 см * 6 см = 30 см² .
Площадь прямоугольника 30 см².

Вычисление прямоугольника: найти P (периметр)

Давайте узнаем, как найти периметр прямоугольника. Как обычно, периметр представляет собой сумму всех сторон фигуры:

P = a + b + a + b

, которое можно записать как:

P = 2 * (a + b)

Возьмем для примера тот же прямоугольник:

Выбираем длину прямоугольника — a = 5 см в нашем случае .
Определитесь с шириной прямоугольника — эл.грамм. b = 6 см .
Сложите эти два значения: a + b = 5 + 6 = 11 см .
Умножьте результат на 2: P = 2 * 11 = 22 см .
Поехали! Периметр нашего прямоугольника 22 см.

Вычисление прямоугольника: найти D (диагональ)

Диагональ прямоугольника — это отрезок, соединяющий две противоположные вершины прямоугольника. Рассчитаем длину диагонали примерного прямоугольника:

Выберите длину прямоугольника — например, a = 5 см .
Определитесь с шириной прямоугольника — например, b = 6 см .
Вычислите a в степени двойки: a² = 25 см² .
Вычислите b в степени двойки: b² = 36 см² .
Сложите эти два значения: a² + b² = 25 + 36 = 61 см² .
Наконец, извлеките квадратный корень из результата: d = √ (a² + b²) = √61 ~ 7,81 см .
Длина по диагонали 7,81 см.

Естественно, вместо того, чтобы вычислять все эти значения вручную, вы можете использовать эту область прямоугольного калькулятора. Вы также можете использовать его в обратном порядке — например, чтобы вычислить ширину прямоугольника с известной длиной и периметром.

Золотой прямоугольник

Особый тип прямоугольника, называемый золотым прямоугольником, показан на изображении выше. Такой прямоугольник удовлетворяет следующему условию:

(a + b) / a = a / b = ϕ

, где φ — золотое сечение, равное 1.618.

Как вы, наверное, помните, отношение — это отношение между двумя величинами, часто представляемое в виде дроби.

Знаете ли вы, что золотой треугольник можно построить, используя только линейку и циркуль ? Всего несколько шагов!

Нарисуйте квадрат.
Проведите линию от середины одной стороны квадрата до противоположного угла.
Нарисуйте круг с радиусом, равным этой линии, с центром в средней точке, как на картинке.
Точка, где круг встречается со стороной расширенного квадрата, является следующим углом золотого прямоугольника.
Найдите последнюю вершину и завершите золотой прямоугольник.

Даааааааааааааааааааааааааааааааааааа! Это было не так уж сложно, правда?

Свойства прямоугольника

Прямоугольники обладают множеством интересных свойств. Прямоугольник:

— это циклический — это означает, что все углы лежат на одной окружности.
— это равноугольный — все углы его углов равны 90 градусам.
— это прямолинейный — его стороны пересекаются под прямым углом.
имеет две линии отражательной симметрии — вертикальную и горизонтальную через центр.
имеет две диагонали, которые делят пополам. Вы можете найти длину диагонали, используя теорему Пифагора.
противоположные стороны прямоугольника параллельны друг другу и имеют одинаковую длину.

Другие менее известные объекты прямоугольной формы:

Пересечение диагоналей — это центр описанной окружности — существует круг, центр которого находится в этой точке, и он проходит через четыре угла.
В прямоугольнике с разной длиной стороны (попросту говоря — не квадрате) невозможно нарисовать вписанную окружность.
Линии, соединяющие середины сторон прямоугольника, образуют ромб, который составляет половину площади прямоугольника. Стороны фигуры параллельны диагоналям.

Вы можете думать и о своей собственной собственности; например по поводу вращения прямоугольника — по бокам или диагонали, чтобы получился цилиндр или конус соответственно.

Прямоугольник и другие формы. Квадрат — это прямоугольник?

TL; DR:

Является ли квадрат прямоугольником? ДА .
Прямоугольник — это параллелограмм? ДА .
Прямоугольник — это ромб? В общем — НЕТ. Только если это квадрат (все углы ромба равны 90 градусам).
Ромб — это прямоугольник? В общем — НЕТ. Только если это квадрат (все стороны прямоугольника одинаковой длины).
Прямоугольник — это четырехугольник? ДА , конечно.
Прямоугольник — это трапеция? ДА .

Хотите знать, является ли квадрат прямоугольником или прямоугольником параллелограммом? Взгляните на картинку, и у вас больше не должно возникнуть сомнений относительно соотношения четырехугольников:

Как читать эту диаграмму? Начнем с нашего прямоугольника. Непосредственно к форме соединены три фигуры: квадрат, параллелограмм и равнобедренная трапеция.Итак, если фигура находится над интересующей нас фигурой — например, квадрат или прямоугольник — мы можем сказать, что:

Каждый квадрат — это прямоугольник , а квадрат — это частный случай прямоугольника .

Для двух других цифр можно указать аналогично:

Каждый прямоугольник — это параллелограмм , а прямоугольник — это частный случай параллелограмма .
Каждый прямоугольник — это трапеция , а прямоугольник — это особый случай трапеции .

Странный забавный факт: какая страна самой прямоугольной формы в мире?

Существует множество различных рейтингов, оценивающих страны — по их регионам, населению, уровню образования или лауреатам Нобелевской премии. Но задумывались ли вы когда-нибудь , кто является победителем конкурса самых прямоугольных стран? Австралийский геостатист Дэвид Барри рассчитал параметр прямоугольности для всех стран мира и составил рейтинг. Он выяснил, что самой прямоугольной страной является Египет, а титул «наименее прямоугольной страны в мире» достается Мальдивам (однако автор признает, что расчеты для стран, состоящих из множества небольших островов, могут быть ужасно ошибочными).Взгляните на таблицу ниже и выберите первые десять стран, а также страны с наименее прямоугольной формой.

Наивысшие баллы в рейтинге прямоугольности. Индекс 1 — идеальный прямоугольник, 0 — бесконечное количество бесконечно малых островов. Таблица адаптирована с веб-страницы мистера Барри, как изображение мира ниже.

Египет — лидер, но это никого не должно удивлять, проверяя очертания этой страны на карте. США находятся в середине рейтинга, в основном из-за неординарности Аляски и Гавайев.Смущает то, что вторая по величине прямоугольность страны — Ватикан — одновременно является четвертой по округлости страной, а Польша, занимающая 5-е место в классификации округлости, занимает 9-е место в рейтинге прямоугольности.

Как это вообще возможно быть прямоугольным и круглым одновременно ?! Как вы можете догадаться, все дело в определении прямоугольности и округлости, которые могут не подходить для сложных или рассеянных форм — и обычно такими примерами являются границы стран, содержащие острые края, небольшие острова или колонии где-то в другой части. Глобус.Если вас интересует эта тема, вы можете взглянуть на это объяснение и обсуждение результатов. Кроме того, в круглом калькуляторе вы найдете специальный абзац о округлости стран с аналогичной таблицей и примерами.

Можно было подумать, что мир было бы легче нарисовать, если бы каждая страна была прямоугольной … Или нет?

Прямоугольник

Форма прямоугольника используется во многих периодических моделях тесселяции. Его можно использовать для облицовки стен из кирпича, плитки для пола, тротуара или различной мозаики.Ниже вы найдете несколько популярных паттернов:

Стыковая кладка — это наиболее распространенный и простой способ укладки плитки, так как плитки укладываются прямыми линиями.

Спусковая связка — типичная для мостовых и кирпичных связок.

Елочка — деревянные полы хорошо смотрятся с таким рисунком.

Basketweave — часто используется для коридоров или уличных дорожек.

Конечно, плитка бывает всех форм и размеров — довольно популярны шестиугольники и восьмиугольники с квадратами. Форма пятиугольника должна быть неправильной, чтобы образовался мозаичный узор.

Прямоугольники в повседневной жизни: прямоугольная форма тела, прямоугольный бассейн, прямоугольная скатерть …

Одной из самых популярных проблем, связанных с прямоугольниками, является тип тела. Если вам интересно, на какую форму ваша фигура больше всего похожа, воспользуйтесь нашим калькулятором формы тела.Все, что вам нужно сделать, это измерить свой бюст, талию, бедра и высокие бедра и ввести значения в инструмент. Тогда вы получите информацию о вашей фигуре. Например, фигура прямоугольника определяется как «мальчишеский» тип телосложения — ваши бедра, талия и бюст примерно одинакового размера. Ваше тело стройно и спортивно. Ознакомьтесь также с нашим калькулятором жировых отложений, который поможет вам оценить процентное содержание жировых отложений в общей массе вашего тела.

Удивительно, но нас окружают прямоугольные предметы.Поэтому наш калькулятор прямоугольников может быть полезен не только на уроках математики, но и в решении повседневных задач. Конечно, вы не найдете идеального прямоугольника в реальности, поскольку он всегда имеет третье измерение; но если он мал по сравнению с двумя другими измерениями, приближение достаточно хорошее.

Прямоугольные скатерти — учитывая размер вашего стола, вы можете узнать, какая скатерть вам понадобится, а также сколько кружевной или подшивной ленты вам понадобится.
Двери или оконное стекло — Ваше оконное стекло разбило шторм или мяч для гольфа? Подсчитайте площадь и оцените стоимость ремонта, учитывая цену за квадратный метр или квадратный метр.
Экраны электронных устройств — планшеты, смартфоны, телевизоры — используйте эту область прямоугольного калькулятора или наш специальный инструмент размера экрана, чтобы оценить, сколько места на стене займет ваш экран — или насколько большой экран вашего телефона хочу купить есть. Если вас интересует плотность пикселей, попробуйте наш калькулятор PPI
Классные доски, зеркала, рамки, холст, листы бумаги, записные книжки, конверты, деньги, флаги, прямоугольные бассейны … Это бесконечный список!

Посмотрите, можете ли вы найти больше прямоугольных предметов вокруг себя? Что вы можете!

Формулы площади

( пи = = 3.141592 …)

Площадь Формулы

Примечание: «ab» означает «а» умножить на «б». «a

²» означает «квадрат», что то же самое, что «а» умножить на «а».

Будьте осторожны !! Количество единиц. Используйте то же самое единиц для всех измерений. Примеры

квадрат = a ²

прямоугольник = ab

параллелограмм = bh

трапеция = h / 2 (b ₁ + b ₂)095

pi r ²

эллипс = pi r ₁ r ₂

треугольник =

, равная половине длины основания, умноженной на высоту треугольник

равносторонний треугольник =

треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C

треугольник, заданный a, b, c = [s (s-a) (s-b) (s-c)] когда s = (a + b + c) / 2 (формула Герона)

правильный многоугольник = (1/2) n sin (360 ° / n) S ²
когда n = количество сторон и S = длина от центра до угла

шт.

Площадь измеряется в «квадратных» единицах.Площадь фигуры количество квадратов, необходимых для его полного покрытия, как плитки на пол.

Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата — это то же самое, это может быть просто длина одной стороны в квадрате.

Если у квадрата одна сторона 4 дюйма, площадь будет равна 4 дюймам. 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в формате ².)

Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается. измерение.

Площадь прямоугольника — это длина сбоку. раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что это площадь?

НЕ ПРАВИЛЬНО …. 4 раза 6 = 24

ПРАВИЛЬНО …. 4 дюйма равно 1/3 фута.