- Определение коэффициента теплопередачи материалов
- Коэффициент теплопроводности материалов таблица, формулы
- Коэффициент теплопроводности теплоизоляционных материалов
- Коэффициенты теплопроводности изоляции
- Расчет коэффициента теплопередачи / ППУ XXI ВЕК – Напыление ППУ
- Коэффициенты теплопроводности
- Шаг 4: Сравниваем. Таблица теплопроводности утеплителей
- Шаг 2: Теория понятие
- Обобщения закона Фурье
- Коэффициенты теплопроводности строительных материалов в таблицах
- Перлитовая
- Теплопроводность гипсовой штукатурки
- Коэффициенты теплопроводности различных веществ
- Теплопроводность готового здания. Варианты утепления конструкций
- Если задумано индивидуальное строительство
- Теплопроводность.
- Таблица теплопроводности теплоизоляционных материалов
- Закон теплопроводности Фурье
- Экономичная штукатурная теплоизоляция.
- Конвекция в атмосфере
- Определение
- Понятие теплопроводности на практике
- Что такое теплопроводность и термическое сопротивление
- Шаг 5: Правила монтажа
- Как рассчитать толщину стен
- Коэффициент теплопроводности.
- Коэффициент теплопроводности — это… Что такое Коэффициент теплопроводности?
- Характеристики теплопередачи функционализированных нанопластинок графена Водные наножидкости
- Abstract
- 1. Введение
- 2. Характеристики наножидкостей
- 3. Определение коэффициента теплопередачи
- 4. Анализ данных
- 5. Результаты
- 6. Выводы
- Благодарности
- Сокращения
- АвторПардиняс участвовал в реализации экспериментальной установки для разработки тестов теплопередачи, Роберто Агромайор определил экспериментальные коэффициенты теплопередачи и перепады давления наножидкостей, а Дэвид Кабалейро выполнил дизайн наножидкостей и их теплофизические характеристики. Роберто Агромайор, Анхель Б. Пардиньяс, Дэвид Кабалейро и Хавьер П. Вальехо проанализировали данные и написали статью. Хосе Фернандес-Сеара и Луис Луго придумали исследование, разработали его дизайн и координировали редактирование рукописи.Все авторы прочитали и одобрили окончательную рукопись.
- Конфликт интересов
- Ссылки
- Frontiers | Численное моделирование корреляции коэффициента теплопередачи для распылительного охлаждения при непрерывной разливке
- Коэффициент теплопередачи повторно используемого бетонного кирпича в сочетании со стеной из изоляционной плиты EPS
- 1. Введение
- 2. Тест коэффициента теплопередачи
- 2.1. Типы стен и свойства материалов
- 2.2. Прибор для испытаний
- 3. Расчет коэффициента теплопередачи Модель
- 3.1. Принципы расчета тестовых значений
- 3.2. Теоретическая расчетная модель
- 3.3. Модель расчета скорректированного значения
- 4. Результаты
- 4.1. Экспериментальные результаты и анализ неопределенностей
- 4.3. Результаты испытаний и теоретические значения
- 4.4. Анализ результатов правильного расчета коэффициента теплопередачи
- 5. Выводы
- Конфликт интересов
- Благодарности
- Общий коэффициент теплопередачи — U-фактор | Определение
- Теплообмен
- Конвертер коэффициента теплопередачи • Термодинамика — Тепло • Компактный калькулятор • Онлайн-конвертеры единиц
Определение коэффициента теплопередачи материалов
Для чего подбирают определенную толщину стены дома?
Естественно для обеспечения необходимых условий проживания:
— прочности и устойчивости;
— её теплотехнических характеристик;
— комфортности проживания в помещении со стенами из данного материала.
Согласно СНИПу 23-02-2003 нормативное значение сопротивления теплопередаче внешней стены дома зависит от региона. В таблице необходимое сопротивление теплопередаче наружней стены в Красноярске будет 4,84 м2·°C/В.
Вычисляем реальное сопротивление теплопередачи стены дома
Значение коэффициента теплопередачи стен зависит от типа и толщины каждого отдельно взятого материала, используемого для их возведения. Для определения этого коэффициента используют показатель Λ — W/(m²·K), т.е нужно разделить толщину материала (м) на коэффициент теплопроводности.
Пример:
Определим коэффициент теплопередачи наружней стены из 3D-панелей
Пенополистирол ПСБ-С-25 — 300 мм
Цементная штукатурка — 250 мм
1.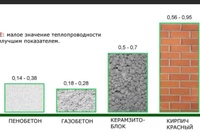 В первую очередь следует определить коэффициенты теплопроводности применяемых материалов. Выбираем из таблицы:
В первую очередь следует определить коэффициенты теплопроводности применяемых материалов. Выбираем из таблицы:
пенополистирол ПСБ-С25 — 0,038 Вт/м*К
штукатурка цементная — 0,9 Вт/м*К
2. Теперь определяем коэффициенты сопротивления теплопередачи по формуле:
R =D/λ, где D — толщина слоя в м; λ — коэффициент теплопроводности W/(m²·K) взятый из таблицы
0,30 / 0,038 = 7,89
0,25 / 0,9 = 0,28
| Наименование материала | Толщина материала, м | Коэффициент теплопроводности, Вт/м*К | Коэффициент сопротивление теплопередачи, м2 °С/Вт |
| Пенополистирол ПСБ-С25 | 0,30 | 0,038 | 7,89 |
| Штукатурка цементная | 0,25 | 0,9 | 0,28 |
3. Теперь просуммируем полученные величины и узнаем общий коэффициент сопротивление теплопередачи наружней стены 7,89 + 0,28 = 8,17 W/(m²·K)
Коэффициент сопротивление теплопередачи наружной стены из 3D-панелей 8,17 W/(m²·K) Рекомендуемое значение для Красноярска 4,84 (из таблицы), таким образом стена из 3D-панелей не только удовлетворяет «строгому» СНиП 23-02-2003, но и превосходит этот показатель, что гарантирует комфортное проживание в таком доме и позволяет экономить ваши деньги на отоплении и кондиционировании.
Определяем толщину стены из других строительных материалов что бы она соответствовала коэффициенту сопротивление теплопередачи наружней стены 8,17 W/(m²·K), как в 3D-панелях.
Используем формулу: D=λ*R, где
D — толщина слоя в м;
λ — коэффициент теплопроводности, W/(m²·K) взятый из таблицы;
R — Коэффициент сопротивление теплопередачи, м2 °С/Вт (в нашем случае это 8,17)
| Наименование материала | Коэффициент теплопроводности, Вт/м*К | Толщина стены, м |
| 3D-панель | 0,55 | |
| Липа, береза, клен, дуб (15% влажности) | 0,15 | 1,23 |
| Керамзитобетон | 0,2 | 1,63 |
| Пенобетон 1000 кг/м3 | 0,3 | 2,45 |
| Сосна и ель вдоль волокон | 0,35 | 2,86 |
| Дуб вдоль волокон | 0,41 | 3,35 |
| Кладка из кирпича на цементно-песчасном растворе | 0,87 | 7,11 |
| Железобетон | 1,7 | 13,89 |
Мы видим из таблицы, что при одинаковом коэффициенте сопротивление теплопередачи 8,17 м2 °С/Вт толщина стен из различных строительных материалов разная, что влияет на размеры и стоимость дома.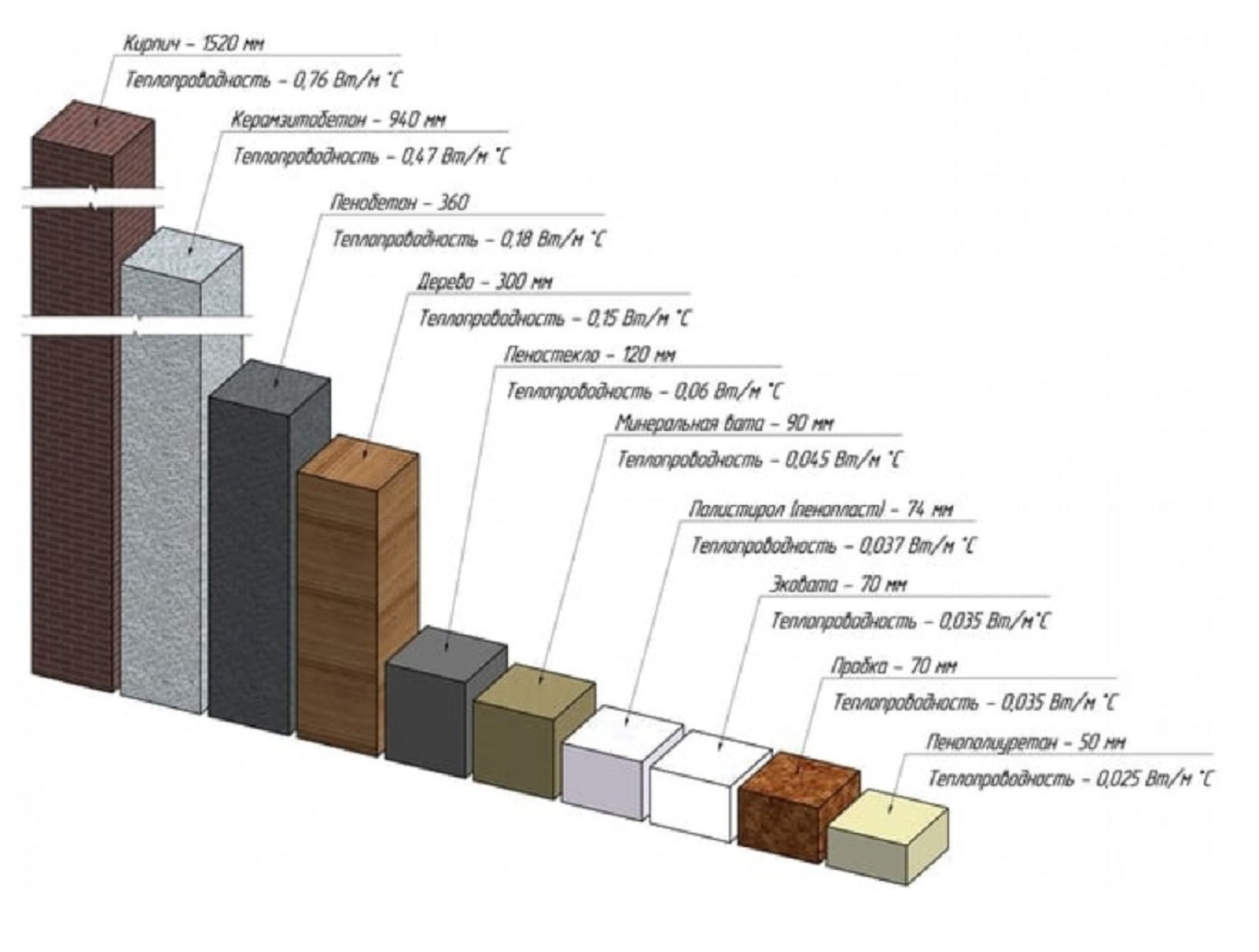
Толщина стен из 3D-панелей 550 мм, а если взять кирпич без утеплителя то нужно стоить стену толщиной 7110 мм.
Коэффициент теплопроводности материалов таблица, формулы
Термин «теплопроводность» применяется к свойствам материалов пропускать тепловую энергию от горячих участков к холодным. Теплопроводность основана на движении частиц внутри веществ и материалов. Способность передавать энергию тепла в количественном измерении – это коэффициент теплопроводности. Круговорот тепловой энергопередачи, или тепловой обмен, может проходить в любых веществах с неравнозначным размещением разных температурных участков, но коэффициент теплопроводности зависим от давления и температуры в самом материале, а также от его состояния – газообразного, жидкого или твердого. Эквивалентная теплопроводимость строительных материалов и утеплителей
Физически теплопроводность материалов равняется количеству тепла, которое перетекает через однородный предмет установленных габаритов и площади за определенный временной отрезок при установленной температурной разнице (1 К).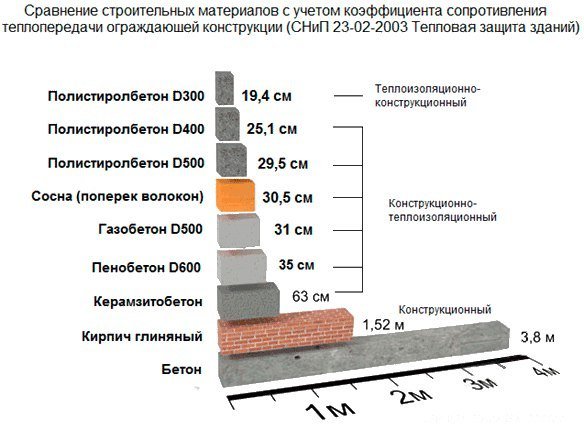 В системе СИ единичный показатель, который имеет коэффициент теплопроводности, принято измерять в Вт/(м•К).
В системе СИ единичный показатель, который имеет коэффициент теплопроводности, принято измерять в Вт/(м•К).
Как рассчитать теплопроводность по закону Фурье
В заданном тепловом режиме плотность потока при передаче тепла прямо пропорциональна вектору максимального увеличения температуры, параметры которой изменяются от одного участка к другим, и по модулю с одинаковой скоростью увеличения температуры по направлению вектора:
q → = − ϰ х grad х (T), где:
- q → – направление плотности предмета, передающего тепло, или объем теплового потока, который протекает по участку за заданную временную единицу через определенную площадь, перпендикулярный всем осям;
- ϰ – удельный коэффициент теплопроводности материала;
- T – температура материала.
Знак «-» в формуле перед «ϰ» указывает, что тепло движется в противоположном направлении от вектора grad х (T)/ – в направлении уменьшения температуры предмета. Эта формула отражает закон Фурье. В интегральном выражении коэффициент теплопередачи согласно закону Фурье будет выглядеть как формула:
Эта формула отражает закон Фурье. В интегральном выражении коэффициент теплопередачи согласно закону Фурье будет выглядеть как формула:
- P = − ϰ х S х ΔT / l, выражается в (Вт/(м•К) х (м2•К) / м = Вт/(м•К) х (м•К) = Вт), где:
- P – общая мощность потерь теплоотдачи;
- S – сечение предмета;
- ΔT – разница температуры по стыкам сторон предмета;
- l – расстояние между стыками сторон предмета – длина фигуры.
Электропроводность и коэффициент теплопередачи
Собственно, коэффициент теплопроводности металлов «ϰ» связан с их удельной электропроводимостью «σ» согласно закону Видемана-Франца, в соответствии с которым коэффициент теплопроводности металлов зависит от удельной электропроводимости прямо пропорционально температуре:
Κ / σ = π2 / 3 х (К / e)2 х T, где:
- К – постоянный коэффициент Больцмана, устанавливающий закономерность между тепловой энергией тела и его температурой;
- e – заряд электрона;
- T – термодинамическая температура предмета.

Коэффициент теплопроводности газовой среды
В газовой среде коэффициент теплопроводности воздуха может рассчитываться по приблизительной формуле:
ϰ ~ 1/3 х p х cv х Λλ х v–, где:
- pv – плотность газовой среды;
- cv – удельная емкость тепловой энергии при одном и том же объеме тела;
- Λλ – расстояние свободного перемещения молекул в газовой среде;
- v– – скорость передачи тепла.
Или:
ϰ = I x К / 3 x π3/3 x d2 √ RT / μ, где:
- i – результат суммирования уровней свободы прямого движения и вращения молекул в газовой среде (для 2-атомных газов i=5, для 1-атомных i=3;
- К – коэффициент Больцмана;
- μ – отношение массы газа к количеству молей газа;
- T – термодинамическая температура;
- d – ⌀ молекул газа;
- R – универсальный коэффициент для газовой среды.

Согласно формуле минимальная теплопроводность материалов существует у тяжелых инертных газов, максимально эффективная теплопроводность строительных материалов – у легких.
Теплопроводимость в газовой разреженной среде
Газовая среда и теплопроводность
Результат по выкладкам выше, по которым делают расчет теплопроводности для газовой среды, от давления не зависит. Но в очень разреженной газовой среде расстояние свободного перемещения молекул зависит не от столкновений частиц, а от препятствий в виде стен резервуара. При этом ограничение перемещения молекул в соответствующих единицах измерения называют высоковакуумной средой, при которой степень теплообмена уменьшается в зависимости от плотности материала и прямо пропорциональна значению давления в резервуаре:
ϰ ~ 1/3 х p х cv х l х v–, где:
i – объем резервуара;
Р – уровень давления в резервуаре.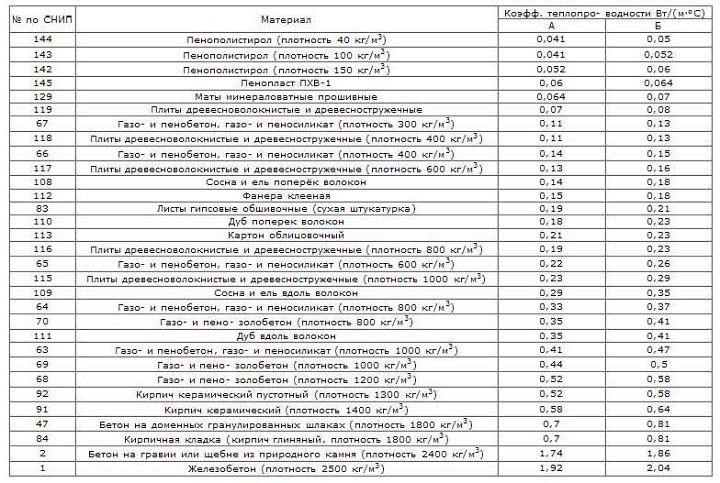
Согласно этой формуле теплопроводность в вакуумной среде стремится к нулевой отметке при глубоком вакууме. Это объясняется тем, что в вакууме частицы, которые передают тепловую энергию, имеют низкую плотность на единицу площади. Но тепловая энергия в вакуумной среде перетекает посредством излучения. В качестве примера можно привести обычный термос, в котором для уменьшения потерь тепловой энергии стенки должны быть двойными и посеребренными, без воздуха между ними. Что такое тепловое излучение
При применении закона Фурье не принимают во внимание инерционность перетекания тепловой энергии, а это значит, что имеется в виду мгновенная передача тепла из любой точки на любое расстояние. Поэтому формулу нельзя использовать для расчетов передачи тепла при протекании процессов, имеющих высокую частоту повторения. Это ультразвуковое излучение, передача тепловой энергии волнами ударного или импульсного типа и т.д. Существует решение по закону Фурье с релаксационным членом:
τ х ∂q / ∂t = − (q + ϰ х ∇T) .
Если релаксация τ мгновенная, то формула превращается в закон Фурье.
Ориентировочная таблица теплопроводности материалов:
| Основа | Значение теплопроводности, Вт/(м•К) |
| Жесткий графен | 4840 +/– 440 – 5300 +/– 480 |
| Алмаз | 1001-2600 |
| Графит | 278,4-2435 |
| Бора арсенид | 200-2000 |
| SiC | 490 |
| Ag | 430 |
| Cu | 401 |
| BeO | 370 |
| Au | 320 |
| Al | 202-236 |
| AlN | 200 |
| BN | 180 |
| Si | 150 |
| Cu3Zn2 | 97-111 |
| Cr | 107 |
| Fe | 92 |
| Pt | 70 |
| Sn | 67 |
| ZnO | 54 |
| Черная сталь | 47-58 |
| Pb | 35,3 |
| Нержавейка | Теплопроводность стали – 15 |
| SiO2 | 8 |
| Высококачественные термостойкие пасты | 5-12 |
| Гранит (состоит из SiO2 68-73 %; Al2O3 12,0-15,5 %; Na2O 3,0-6,0 %; CaO 1,5-4,0 %; FeO 0,5-3,0 %; Fe2O3 0,5-2,5 %; К2О 0,5-3,0 %; MgO 0,1-1,5 %; TiO2 0,1-0,6 %) | 2,4 |
| Бетонный раствор без заполнителей | 1,75 |
| Бетонный раствор со щебнем или с гравием | 1,51 |
| Базальт (состоит из SiO2 – 47-52%, TiO2 – 1-2,5%, Al2O3 – 14-18%, Fe2O3 – 2-5%, FeO – 6-10%, MnO – 0,1-0,2%, MgO – 5-7%, CaO – 6-12%, Na2O – 1,5-3%, K2O – 0,1-1,5%, P2O5 – 0,2-0,5 %) | 1,3 |
| Стекло (состоит из SiO2, B2O3, P2O5, TeO2, GeO2, AlF3 и т. | 1-1,15 |
| Термостойкая паста КПТ-8 | 0,7 |
| Бетонный раствор с наполнителем из песка, без щебня или гравия | 0,7 |
| Вода чистая | 0,6 |
| Силикатный или красный кирпич | 0,2-0,7 |
| Масла на основе силикона | 0,16 |
| Пенобетон | 0,05-0,3 |
| Газобетон | 0,1-0,3 |
| Дерево | Теплопроводность дерева – 0,15 |
| Масла на основе нефти | 0,125 |
| Снег | 0,10-0,15 |
| ПП с группой горючести Г1 | 0,039-0,051 |
| ЭППУ с группой горючести Г3, Г4 | 0,03-0,033 |
| Стеклянная вата | 0,032-0,041 |
| Вата каменная | 0,035-0,04 |
| Воздушная атмосфера (300 К, 100 кПа) | 0,022 |
| Гель на основе воздуха | 0,017 |
| Аргон (Ar) | 0,017 |
| Вакуумная среда | 0 |
Приведенная таблица теплопроводности учитывает теплопередачу посредством теплового излучения и теплообмена частиц.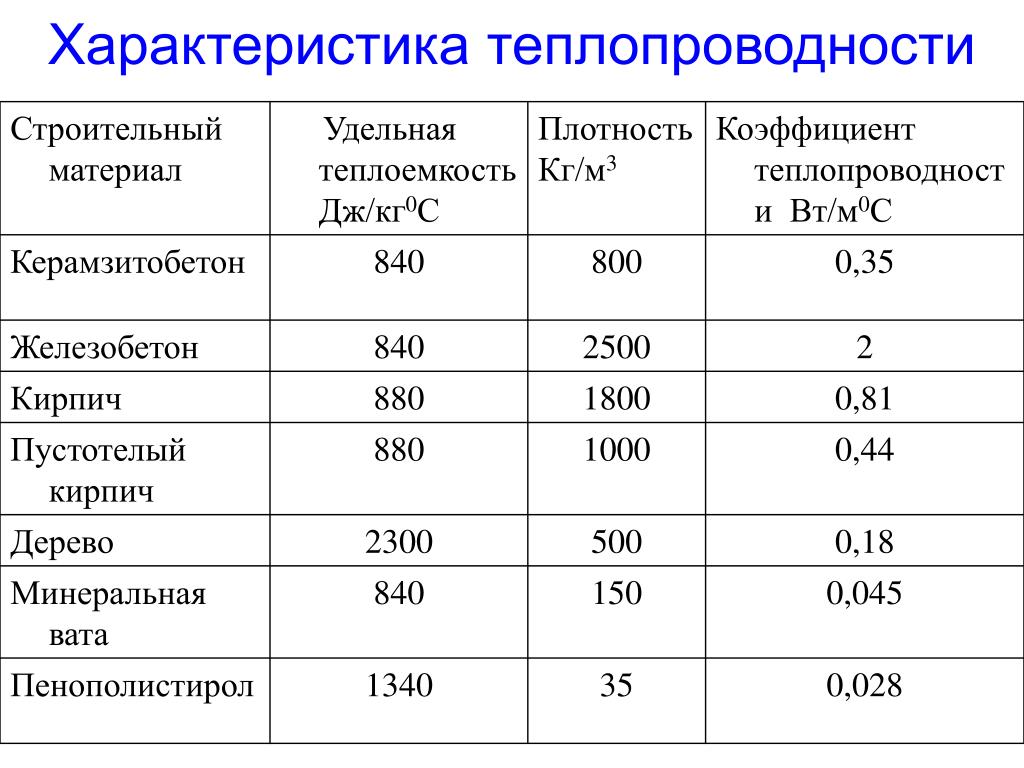 Так как вакуум не передает тепло, то оно перетекает при помощи солнечного излучения или другого типа генерации тепла. В газовой или жидкой среде слои с разной температурой смешиваются искусственно или естественным способом.
Так как вакуум не передает тепло, то оно перетекает при помощи солнечного излучения или другого типа генерации тепла. В газовой или жидкой среде слои с разной температурой смешиваются искусственно или естественным способом.
Проводя расчет теплопроводности стены, необходимо принимать во внимание, что теплопередача сквозь стеновые поверхности меняется от того, что температура в здании и на улице всегда разная, и зависит от площади всех поверхностей дома и от теплопроводности стройматериалов.
Чтобы количественно оценить теплопроводность, ввели такое значение, как коэффициент теплопроводности материалов. Он показывает, как тот или иной материал способен передавать тепло. Чем выше это значение, например, коэффициент теплопроводности стали, тем эффективнее сталь будет проводить тепло.
- При утеплении дома из древесины рекомендуется выбирать стройматериалы с низким коэффициентом.
- Если стена кирпичная, то при значении коэффициента 0,67 Вт/(м2•К) и толщине стены 1 м при ее площади 1 м2 при разнице наружной и внутридомовой температуры 10С кирпич будет пропускать 0,67 Вт энергии. При разнице температур 100С кирпич будет пропускать 6,7 Вт и т.д.
Стандартное значение коэффициента теплопроводимости теплоизоляции и других строительных материалов верно для толщины стены 1 м. Чтобы провести расчет теплопроводности поверхности другой толщины, следует коэффициент поделить на выбранное значение толщины стены (метры). Ориентировочные показатели коэффициентов теплопроводимости
В СНиП и при проведении расчетов фигурирует термин «тепловое сопротивление материала», он означает обратную теплопроводность. То есть при теплопроводности листа пенопласта 10 см и его теплопроводности 0,35 Вт/(м2•К) тепловое сопротивление листа – 1 / 0,35 Вт/(м2•К) = 2,85 (м2•К)/Вт.
Ниже – таблица теплопроводности для востребованных строительных материалов и теплоизоляторов:
| Стройматериалы | Коэффициент теплопроводимости, Вт/(м2•К) |
| Плиты из алебастра | 0,47 |
| Al | 230 |
| Шифер асбоцементный | 0,35 |
| Асбест (волокно, ткань) | 0,15 |
| Асбоцемент | 1,76 |
| Асбоцементные изделия | 0,35 |
| Асфальт | 0,73 |
| Асфальт для напольного покрытия | 0,84 |
| Бакелит | 0,24 |
| Бетон с заполнителем щебнем | 1,3 |
| Бетон с заполнителем песком | 0,7 |
| Пористый бетон – пено- и газобетон | 1,4 |
| Сплошной бетон | 1,75 |
| Термоизоляционный бетон | 0,18 |
| Битумная масса | 0,47 |
| Бумажные материалы | 0,14 |
| Рыхлая минвата | 0,046 |
| Тяжелая минвата | 0,05 |
| Вата – теплоизолятор на основе хлопка | 0,05 |
| Вермикулит в плитах или листах | 0,1 |
| Войлок | 0,046 |
| Гипс | 0,35 |
| Глиноземы | 2,33 |
| Гравийный заполнитель | 0,93 |
| Гранитный или базальтовый заполнитель | 3,5 |
| Влажный грунт, 10% | 1,75 |
| Влажный грунт, 20% | 2,1 |
| Песчаники | 1,16 |
| Сухая почва | 0,4 |
| Уплотненный грунт | 1,05 |
| Гудроновая масса | 0,3 |
| Доска строительная | 0,15 |
| Фанерные листы | 0,15 |
| Твердые породы дерева | 0,2 |
| ДСП | 0,2 |
| Дюралюминиевые изделия | 160 |
| Железобетонные изделия | 1,72 |
| Зола | 0,15 |
| Известняковые блоки | 1,71 |
| Раствор на песке и извести | 0,87 |
| Смола вспененная | 0,037 |
| Природный камень | 1,4 |
| Картонные листы из нескольких слоев | 0,14 |
| Каучук пористый | 0,035 |
| Каучук | 0,042 |
| Каучук с фтором | 0,053 |
| Керамзитобетонные блоки | 0,22 |
| Красный кирпич | 0,13 |
| Пустотелый кирпич | 0,44 |
| Полнотелый кирпич | 0,81 |
| Сплошной кирпич | 0,67 |
| Шлакокирпич | 0,58 |
| Плиты на основе кремнезема | 0,07 |
| Латунные изделия | 110 |
| Лед при температуре 00С | 2,21 |
| Лед при температуре -200С | 2,44 |
| Лиственное дерево при влажности 15% | 0,15 |
| Медные изделия | 380 |
| Мипора | 0,086 |
| Опилки для засыпки | 0,096 |
| Сухие опилки | 0,064 |
| ПВХ | 0,19 |
| Пенобетон | 0,3 |
| Пенопласт марки ПС-1 | 0,036 |
| Пенопласт марки ПС-4 | 0,04 |
| Пенопласт марки ПХВ-1 | 0,05 |
| Пенопласт марки ФРП | 0,044 |
| ППУ марки ПС-Б | 0,04 |
| ППУ марки ПС-БС | 0,04 |
| Лист из пенополиуретана | 0,034 |
| Панель из пенополиуретана | 0,024 |
| Облегченное пеностекло | 0,06 |
| Тяжелое вспененное стекло | 0,08 |
| Пергаминовые изделия | 0,16 |
| Перлитовые изделия | 0,051 |
| Плиты на цементе и перлите | 0,085 |
| Влажный песок 0% | 0,33 |
| Влажный песок 0% | 0,97 |
| Влажный песок 20% | 1,33 |
| Обожженный камень | 1,52 |
| Керамическая плитка | 1,03 |
| Плитка марки ПМТБ-2 | 0,035 |
| Полистирол | 0,081 |
| Поролон | 0,04 |
| Раствор на основе цемента без песка | 0,47 |
| Плита из натуральной пробки | 0,042 |
| Легкие листы из натуральной пробки | 0,034 |
| Тяжелые листы из натуральной пробки | 0,05 |
| Резиновые изделия | 0,15 |
| Рубероид | 0,17 |
| Сланец | 2,100 |
| Снег | 1,5 |
| Хвойная древесина влажностью 15% | 0,15 |
| Хвойная смолистая древесина влажностью 15% | 0,23 |
| Стальные изделия | 52 |
| Стеклянные изделия | 1,15 |
| Утеплитель стекловата | 0,05 |
| Стекловолоконные утеплители | 0,034 |
| Стеклотекстолитовые изделия | 0,31 |
| Стружка | 0,13 |
| Тефлоновое покрытие | 0,26 |
| Толь | 0,24 |
| Плита на основе цементного раствора | 1,93 |
| Цементно-песчаный раствор | 1,24 |
| Чугунные изделия | 57 |
| Шлак в гранулах | 0,14 |
| Шлак зольный | 0,3 |
| Шлакобетонные блоки | 0,65 |
| Сухие штукатурные смеси | 0,22 |
| Штукатурный раствор на основе цемента | 0,95 |
| Эбонитовые изделия | 0,15 |
Кроме того, необходимо учитывать теплопроводность утеплителей из-за их струйных тепловых потоков. В плотной среде возможно «переливание» квазичастиц из одного нагретого стройматериала в другой, более холодный или более теплый, через поры субмикронных размеров, что помогает распространять звук и тепло, даже если в этих порах будет абсолютный вакуум.
Коэффициент теплопроводности теплоизоляционных материалов
Одной из основных характеристик теплоизоляционных материалов является теплопроводность. Почти у всех есть понимание, что чем она меньше, тем лучше. Но что означает этот термин и что он нам дает? Как сравнить два типа изоляции, используя этот параметр? Предлагаем разобраться
Что такое коэффициент теплопроводности?
Согласно определения в своде правил СП 61.13330.2012:
Коэффициент теплопроводности — количество тепла, которое передается за единицу времени на единицу площади поверхности при температурном градиенте (изменении температуры), равном единице. Обозначается символом λ (лямбда), единица измерения Вт/(м·К).
Само свойство теплопроводности определяет способность материалов передавать тепловую энергию от более горячего тела к более холодному.
От чего зависит коэффициент?
При изучении данной характеристики было определено, что существует зависимость коэффициента теплопроводности от температуры и других параметров:
- параметров состояния — температуры, давления
- свойств — плотность, влажность, структуры
При изменении данных свойств и параметров меняется и теплопроводность.
Обозначение λ0 определяет коэффициент теплопроводности, который получен при испытаниях при температуре 0 °С. При этом температура является среднеарифметическим значением от: (температура на внешней поверхности изоляционного материала + температура на изолируемой поверхности)/2.
По аналогии λ20 — это коэффициент полученный при проведении замеров при температуре 20 °С.
Как это использовать на практике?
Данная характеристика позволяет определить возможность использования теплоизоляции в определенных условиях. Кроме того, Вы можете сравнивать различные виды теплоизоляционных материалов и выбирать наиболее подходящий.
Коэффициент теплопроводности теплоизоляционных материалов
1. Вспененный полиэтилен. Сравнивая продукцию из вспененного полиэтилена можно определить, что при температуре 10 °С минимальным коэффициентом теплопроводности будет обладать теплоизоляция ALMALEN — 0.032 Вт/мК — 0.034 Вт/мК. Это наименьший показатель в данном классе.
2. Вспененный каучук. В данной группе теплоизоляции можно выделить AF/Armaflex — для неё λ0 ºC ≤ 0,033 Вт/(м·К).
3. Базальтовый утеплитель. При выборе материалов из базальтовой ваты, стоит обратить внимание на Цилиндры Paroc HVAC Section AluCoat T — λ10 ºC ≤ 0,034 В/(м·К).
Правильно ли сравнивать только по λ?
Прежде всего стоит сравнивать показатели, определенные при одной температуре. Существуют различные стандарты определения коэффициента. Могут отличаться «стандартные тепловые режимы»: согласно ГОСТ 7076-99 показатель определяется при 25 °С, а при использовании европейского стандарта EN 12667:2001, нормой является 10 °С.
Также учитывайте планируемые условия эксплуатации материала: влажность, возможное воздействие пара, наличие критических перепадов температуры и так далее.
1 | Асбестовый матрац, заполненный совелитом | 0,087+0,00012* tт |
2 | Асбестовый матрац, заполненный стекловолокном | 0,058+0,00023* tт |
3 | Асботкань в несколько слоев | 0,13+0,00026* tт |
4 | Асбестовый шнур | 0,12+0,00031* tт |
5 | Асбестовый шнур (ШАОН) | 0,13+0,00026* tт |
6 | Асбопухшнур (ШАП) | 0,093+0,0002* tт |
7 | Асбовермикулитовые изделия марки 250 | 0,081+0,00023* tт |
8 | Асбовермикулитовые изделия марки 300 | 0,087+0,00023* tт |
9 | Битумоперлит | 0,12+0,00023* tт |
10 | Битумокерамзит | 0,13+0,00023* tт |
11 | Битумовермикулит | 0,13+0,00023* tт |
12 | Вулканитовые плиты марки 300 | 0,074+0,00015* tт |
13 | Диатомовые изделия марки 500 | 0,116+0,00023* tт |
14 | Диатомовые изделия марки 600 | 0,14+0,00023* tт |
15 | Известково-кремнеземистые изделия марки 200 | 0,069+0,00015* tт |
16 | Маты минераловатные прошивные марки 100 | 0,045+0,0002* tт |
17 | Маты минераловатные прошивные марки 125 | 0,049+0,0002* tт |
18 | Маты и плиты из минеральной ваты марки 75 | 0,043+0,00022* tт |
19 | Маты и полосы из непрерывного стекловолокна | 0,04+0,00026* tт |
20 | Маты и плиты стекловатные марки 50 | 0,042+0,00028* tт |
21 | Пенобетонные изделия | 0,11+0,0003* tт |
22 | Пенопласт ФРП-1 и резопен группы 100 | 0,043+0,00019* tт |
23 | Пенополимербетон | 0,07 |
24 | Пенополиуретан | 0,05 |
25 | Перлитоцементные изделия марки 300 | 0,076+0,000185* tт |
26 | Перлитоцементные изделия марки 350 | 0,081+0,000185* tт |
27 | Плиты минераловатные полужесткие марки 100 | 0,044+0,00021* tт |
28 | Плиты минераловатные полужесткие марки 125 | 0,047+0,000185* tт |
29 | Плиты и цилиндры минераловатные марки 250 | 0,056+0,000185* tт |
30 | Плиты стекловатные полужесткие марки 75 | 0,044+0,00023* tт |
31 | Полуцилиндры и цилиндры минераловатные марки 150 | 0,049+0,0002* tт |
32 | Полуцилиндры и цилиндры минераловатные марки 200 | 0,052+0,000185* tт |
33 | Совелитовые изделия марки 350 | 0,076+0,000185* tт |
34 | Совелитовые изделия марки 400 | 0,078+0,000185* tт |
35 | Скорлупы минераловатные оштукатуренные | 0,069+0,00019* tт |
36 | Фенольный поропласт ФЛ монолит | 0,05 |
37 | Шнур минераловатный марки 200 | 0,056+0,000185* tт |
38 | Шнур минераловатный марки 250 | 0,058+0,000185* tт |
39 | Шнур минераловатный марки 300 | 0,061+0,000185* tт |
Расчет коэффициента теплопередачи / ППУ XXI ВЕК – Напыление ППУ
Эта статья поможет вам самостоятельно выяснить, какие потери тепла вы несете. Для этого необходимо знать четыре основные термина. С первого взгляда они означают одно и то же, поэтому и надо рассмотреть их внимательнее.
Коэффициент теплопередачи
Коэффициент теплопередачи показывает, как хорошо элемент конструкции (крыша, стена, пол) проводит тепло. Чем ниже этот показатель, тем хуже пропускается тепло и тем лучше теплоизоляция.
Определение коэффициента теплопередачи звучит следующим образом: потеря энергии квадратным метром поверхности при разности температур внешней и внутренней. Это определение влечет за собой взаимосвязь ватт, квадратных метров и Кельвина W/(m2·K).
Кельвин – это единица температуры. 0 Кельвинов – минимально возможное значение температуры. При разности температур значения Кельвина совпадают с градусами по Цельсию.Следующий пример с неизолированной стеной в старой постройке показывает значение коэффициента теплопередачи.В начале 20 века внешние стены дома строили из полнотелого кирпича толщиной 24 см, с двух сторон стена покрывалась штукатуркой толщиной 1,5 см. коэффициент теплопередачи такой стены примерно составляет 2 W/(m2·K).
При разности температур в 1Кельвин (например 21 градус внутри помещения и 20 снаружи) потеря энергии составляет 2 Ватта за квадратный метр. Стена площадью 30 метров квадратных (12*2,5) теряет примерно 60 Ватт.
При понижении внешней температуры соответственно увеличивается потеря энергии. При внешней температуре 0, разница составит 21 градус, а потеря тепла 21 Kельвин x 60 Ватт/Kельвин = 1260 Ватт или 1,26 кВатт. За 24 часа получается 24ч х 1,26 кВатт=30 кВатт/сут., что соответствует расходу топлива объемом 3 литра.
Коэффициент теплопередачи – это предпочтительный способ сравнения конструкций с энергетической точки зрения.
Теплопроводность лямбда λ
Теплопроводность – это свойство материала. Она показывает, насколько хорошо материал проводит тепло и не зависит от его плотности. Теплопроводность подходит для сравнения различных изоляционных материалов, но не для архитектурных конструкций. Теплопроводность – это тепловой ток (Ватт) на разность температур на площадь поперечного сечения умножить на толщину материала. Чем больше толщина материала, тем меньше теплового тока (и наоборот: чем больше площадь поперечного сечения, тем больше теплового тока). Теплопроводность считается по формуле W/(m·K). Но это не означает «Ватт разделить на метр, умноженный на Кельвин». А «Ватт, разделить на метр квадратный(поперечное сечение)умножить на метр (толщина материала) разделить на Кельвин»
Если разделить теплопроводность на толщину материала, то получится коэффициент пропуска тепла с единицей измерения тепловой ток(Ватт) на квадратный метр поверхности и на Кельвин. Эта формула совпадает с коэффициентом теплопередачи, но значения этих понятий различны. Коэффициент теплопередачи учитывает термическое сопротивление воздуха в помещении на стену, также как внешнего воздуха на внешнюю стену. В расчетах коэффициента теплопередачи расчет ведется исходя из разницы в температуре воздуха, а в коэффициенте пропуска тепла – в температуре материалов.
Сопротивление пропуску тепла R
Сопротивление пропуску тепла является обратной величиной коэффициенту пропуска тепла R = d/λ. D при этом толщина слоя. Сопротивление пропуску тепла описывает, как определенный материал не пропускает тепло. Чем выше сопротивление пропуску тепла, тем лучше теплоизоляция. Единица измерения m2K/W.
Коэффициенты теплопроводности
Шаг 4: Сравниваем. Таблица теплопроводности утеплителей
В таблице приводится сравнение утеплителей по теплопроводности заявленной производителями и соответствующие ГОСТам:
| Наименование материала | Коэффициент теплопроводности Ват/м2 |
|---|---|
| Пенопласт | 0.03 |
| Минвата | 0,049-0,6 |
| Пенофол | 0,037-0,049 |
| Пеноизол | 0,21-0,24 |
| Пеностекло | 0.08 |
| Пенополиуретан (ППУ) | 0.02 |
| Эковата (целюлоза) | 0.04 |
Сравнительная таблица теплопроводности строительных материалов, которые не принято считать утеплителями:
| Наименование материала | Коэффициент теплопроводности Ват/м2 |
| Бетон | 1.51 |
| Гранит | 3.49 |
| Мрамор | 2.91 |
| Сталь | 58 |
Показатель теплопередачи лишь указывает на скорость передачи тепла от одной молекуле к другой. Для реальной жизни этот показатель не так важен. А вот без теплового расчета стены не обойтись. Сопротивление теплопередаче — величина обратная теплопроводности. Речь идет о способности материала (утеплителя) задерживать тепловой поток. Чтобы рассчитать сопротивление теплопередаче нужно разделить толщину на коэффициент теплопроводности. На примере ниже показан расчет теплового сопротивления стены из бруса толщиной 180 мм.
Как видно, теплосопротивление такой стены составит 1,5. Достаточно? Это зависит от региона. В примере показан расчет для Красноярска. Для этого региона нужный коэффициент сопротивления ограждающих конструкций установлен на уровне 3,62. Ответ ясен. Даже для Киева, который намного южнее данный показатель равняется 2,04.
А значит, способности деревянного дома сопротивляться потере тепла недостаточно. Необходимо утепление, а уже, каким материалом — рассчитывайте по формуле.
Шаг 2: Теория понятие
Из школьного курса физики, скорее всего, помните, что существует три вида теплопередачи:
- Конвекция;
- Излучение;
- Теплопроводность.
А значит теплопроводность — это вид теплопередачи или перемещения тепловой энергии. Это связано с внутренней структурой тел. Одна молекула передает энергию другой. А теперь хотите небольшой тест?
Какой вид веществ пропускает (передает) больше всего энергии?
- Твердые тела?
- Жидкости?
- Газы?
Правильно, больше всего передает энергию кристаллическая решетка твердых тел. Их молекулы находятся ближе друг к другу и поэтому могут взаимодействовать эффективнее. Самой низкой теплопроводностью обладают газы. Их молекулы находятся на наибольшем удалении друг от друга.
Обобщения закона Фурье
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье неприменим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. п. Инерционность в уравнения переноса первым ввел Максвелл, а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:
\tau\frac{\partial\mathbf{q}}{\partial t}=-\left(\mathbf{q}+\varkappa\,\nabla T\right).
Если время релаксации \tau пренебрежимо мало, то это уравнение переходит в закон Фурье.
Коэффициенты теплопроводности строительных материалов в таблицах
Сегодня очень остро стоит вопрос рационального использования ТЭР. Непрерывно прорабатываются пути экономии тепла и энергии с целью обеспечения энергетической безопасности развития экономики как страны, так и каждой отдельной семьи.
Создание эффективных энергоустановок и систем теплоизоляции (оборудования, обеспечивающего наибольший теплообмен (например, паровых котлов) и, наоборот, от которого он нежелателен (плавильные печи)) невозможно без знания принципов теплопередачи.
Изменились подходы к тепловой защите зданий, возросли требования к строительным материалам. Любой дом нуждается в утеплении и системе отопления. Поэтому при теплотехническом расчёте ограждающих конструкций важен расчёт показателя теплопроводности.
Перлитовая
Это одна из разновидностей декоративных штукатурок, которая состоит из вулканических пород. В состав штукатурки входят особые кислые стекла, которые придают покрытию эстетичный внешний вид и добавляют различные практичные качества. Уникальная способность, которой обладает материал, – вспенивание и увеличение в размерах при нагревании. Надо сказать, что перлитовая штукатурка способна увеличиться в объеме в 10 раз. Благодаря этому получается внешне плотный, но достаточно легкий слой для основной поверхности. Плотность слоя может колебаться в пределах 350…800 кг/м 3 , за счет чего колеблется и теплопроводность штукатурки – 0,13…0,9.
Есть такое понятие «сухая штукатурка». Для незнающих в строительной терминологии это означает обыкновенный гипсокартон. По сути, листы состоят из тех же элементов, что и обычная гипсовая штукатурка (жидкая), за исключением того, что они высушены, спрессованы, сформованы и укреплены на картонных листах. Теплопроводность сухой штукатурки также будет зависеть от плотности материала. Средний коэффициент теплопроводности равен 0.21.
Известковая
Наиболее распространенный вид штукатурки для внутренних работ. Одним из главных ее качеств можно назвать чистую белизну, что отлично подходит под дальнейшие финишные работы, в особенности окрашивание или нанесение декоративных жидких обоев. Состоит смесь из гашеной извести, речного песка. Пропорции могут быть разными. Теплопроводность при плотности 1500 кг/м 3 будет равна 0.7.
Для каждой из смесей предусмотрены свои показатели, которые обозначаются на упаковке. Надо сказать, что бумажный мешок сухой смеси – инструкция не только по эксплуатации, но и составу. Там можно найти основные свойства каждого из составов.
Теплопроводность гипсовой штукатурки
Паропроницаемость гипсовой штукатурки нанесенной на поверхность зависит от замешивания. Но если сравнить ее с обычной, то проницаемость гипсовой штукатурки составляет 0,23 Вт/м×°С, а цементной достигает 0,6÷0,9 Вт/м×°С. Такие расчеты позволяю говорить о том что паропроницаемость гипсовой штукатурки намного ниже.
Благодаря низкой проницаемости снижется коэффициент теплопроводности гипсовой штукатурки, что позволяет увеличить тепло в помещении. Гипсовая штукатурка отлично удерживает тепло в отличии от :
- известково-песчаной;
- бетонной штукатурки.
Благодаря низкой теплопроводности гипсовой штукатурки стены остаются теплыми даже в сильный мороз снаружи помещения.
Коэффициенты теплопроводности различных веществ
| Материал | Теплопроводность, /(·) |
| Графен | 4840±440 — 5300±480 |
| Алмаз | 1001—2600 |
| Графит | 278,4—2435 |
| Карбид кремния | 490 |
| Серебро | 430 |
| Медь | 401 |
| Оксид бериллия | 370 |
| Золото | 320 |
| Алюминий | 202—236 |
| Нитрид алюминия | 200 |
| Нитрид бора | 180 |
| Кремний | 150 |
| Латунь | 97—111 |
| Хром | 107 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Оксид цинка | 54 |
| Сталь[какая? ] | 47 |
| Свинец | 35,3 |
| Кварц | 8 |
| Гранит | 2,4 |
| Бетон сплошной | 1,75 |
| Бетон на гравии или щебне из природного камня | 1,51 |
| Базальт | 1,3 |
| Стекло | 1-1,15 |
| Термопаста КПТ-8 | 0,7 |
| Бетон на песке | 0,7 |
| Вода при нормальных условиях | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Силиконовое масло | 0,16 |
| Пенобетон | 0,05—0,3 |
| Древесина | 0,15 |
| Нефтяные масла | 0,12 |
| Свежий снег | 0,10—0,15 |
| Пенополистирол (горючесть Г1) | 0,038-0,052 |
| Экструдированный пенополистирол (горючесть Г3 и Г4) | 0,029-0,032 |
| Стекловата | 0,032-0,041 |
| Каменная вата | 0,034-0,039 |
| Воздух (300 K, 100 кПа) | 0,022 |
| Аэрогель | 0,017 |
| Аргон (273-320 K, 100 кПа) | 0,017 |
| Аргон (240-273 K, 100 кПа) | 0,015 |
| Вакуум (абсолютный) | 0 (строго) |
Также нужно учитывать передачу тепла из-за конвекции молекул и излучения. Например, при полной нетеплопроводности вакуума, тепловая энергия передаётся излучением (Солнце, инфракрасные теплогенераторы). В газах и жидкостях происходит перемешивание разнотемпературных слоёв естественным путём или искусственно (примеры принудительного перемешивания — фены, электрочайники). Также в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепловой энергии, даже если зазоры представляют собой идеальный вакуум.
Теплопроводность готового здания. Варианты утепления конструкций
При разработке проекта постройки необходимо учесть все возможные варианты и пути потери тепла. Большое его количество может уходить через:
- стены – 30%;
- крышу – 30%;
- двери и окна – 20%;
- полы – 10%.
Теплопотери неутепленного частного дома
При неверном расчете теплопроводности на этапе проектирования, жильцам остается довольствоваться только 10% тепла, получаемого от энергоносителей. Именно поэтому дома, возведенные из стандартного сырья: кирпича, бетона, камня рекомендуют дополнительно утеплять. Идеальная постройка согласно таблице теплопроводности строительных материалов должна быть выполнена полностью из теплоизолирующих элементов. Однако малая прочность и минимальная устойчивость к нагрузкам ограничивает возможности их применения.
Нужно знать! При обустройстве правильной гидроизоляции любого утеплителя высокая влажность не повлияет на качество теплоизоляции и сопротивление постройки теплообмену будет значительно выше.
Сравнительный график коэффициентов теплопроводности некоторых строительных материалов и утеплителей
Самым распространенным вариантом сочетание несущей конструкции из высокопрочных материалов с дополнительным слоем теплоизоляции. Сюда можно отнести:
- Каркасный дом. При его постройке каркасом из древесины обеспечивается жесткость всей конструкции, а укладка утеплителя производится в пространство между стойками. При незначительном уменьшении теплообмена в некоторых случая может потребоваться утепление еще и снаружи основного каркаса.
- Дом из стандартных материалов. При выполнении стен из кирпича, шлакоблоков, утепление должно проводиться по наружной поверхности конструкции.
Необходимая тепло- и гидроизоляция для сохранения тепла в частном доме
Если задумано индивидуальное строительство
При возведении дома важно учитывать технические характеристики всех составляющих (материала для стен, кладочного раствора, будущего утепления, гидроизоляционных и пароотводящих плёнок, финишной отделки). Для понимания, какие стены наилучшим образом будут сохранять тепло, нужно проанализировать коэффициент теплопроводности не только материала для стен, но и строительного раствора, что видно из таблицы ниже:
Для понимания, какие стены наилучшим образом будут сохранять тепло, нужно проанализировать коэффициент теплопроводности не только материала для стен, но и строительного раствора, что видно из таблицы ниже:
| Номер п/п | Материал для стен, строительный раствор | Коэффициент теплопроводности по СНиП |
| 1. | Кирпич | 0,35 – 0,87 |
| 2. | Саманные блоки | 0,1 – 0,44 |
| 3. | Бетон | 1,51 – 1,86 |
| 4. | Пенобетон и газобетон на основе цемента | 0,11 – 0,43 |
| 5. | Пенобетон и газобетон на основе извести | 0,13 – 0,55 |
| 6. | Ячеистый бетон | 0,08 – 0,26 |
| 7. | Керамические блоки | 0,14 – 0,18 |
| 8. | Строительный раствор цементно-песчаный | 0,58 – 0,93 |
| 9. | Строительный раствор с добавлением извести | 0,47 – 0,81 |
Важно. Из приведённых в таблице данных видно, что у каждого строительного материала довольно большой разброс в показателях коэффициента теплопроводности.. Это связано с несколькими причинами:
Это связано с несколькими причинами:
- Плотность. Все утеплители выпускаются или укладываются (пеноизол, эковата) различной плотности. Чем ниже плотность (больше присутствует воздуха в теплоизоляционной структуре), тем ниже проводимость тепла. И, наоборот, у очень плотных утеплителей этот коэффициент выше.
- Вещество, из которого производят (основа). Например, кирпич бывает силикатным, керамическим, глиняным. От этого зависит и коэффициент теплопроводности.
- Количество пустот. Это касается кирпича (пустотелый и полнотелый) и теплоизоляции. Воздух – самый худший проводник тепла. Коэффициент его теплопроводимости – 0,026. Чем больше пустот, тем ниже этот показатель.
Строительный раствор хорошо проводит тепло, поэтому любые стены рекомендуется утеплять.
Теплопроводность.
Так что же такое теплопроводность? С точки зрения физики теплопроводность – это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).
Можно сказать проще, теплопроводность – это способность материала проводить тепло. Если внутри тела имеется разность температур, то тепловая энергия переходит от более горячей его части к более холодной. Передача тепла происходит за счет передачи энергии при столкновении молекул вещества. Происходит это до тех пор, пока температура внутри тела не станет одинаковой. Такой процесс может происходить в твердых, жидких и газообразных веществах.
На практике, например в строительстве при теплоизоляции зданий, рассматривается другой аспект теплопроводности, связанный с передачей тепловой энергии. В качестве примера возьмем «абстрактный дом». В «абстрактном доме» стоит нагреватель, который поддерживает внутри дома постоянную температуру, скажем, 25 °С. На улице температура тоже постоянная, например, 0 °С. Вполне понятно, что если выключить обогреватель, то через некоторое время в доме тоже будет 0 °С. Все тепло (тепловая энергия) через стены уйдет на улицу.
Чтобы поддерживать температуру в доме 25 °С, нагреватель должен постоянно работать. Нагреватель постоянно создает тепло, которое постоянно уходит через стены на улицу.
Таблица теплопроводности теплоизоляционных материалов
Чтобы в доме было проще сохранять тепло зимой и прохладу летом, теплопроводность стен, пола и кровли должна быть не менее определенной цифры, которая рассчитывается для каждого региона. Состав «пирога» стен, пола и потолка, толщина материалов берутся с таким учетом чтобы суммарная цифра была не меньше (а лучше — хоть немного больше) рекомендованной для вашего региона.
Коэффициент теплопередачи материалов современных строительных материалов для ограждающих конструкций
При выборе материалов надо учесть, что некоторые из них (не все) в условиях повышенной влажности проводят тепло гораздо лучше. Если при эксплуатации возможно возникновение такой ситуации на продолжительный срок, в расчетах используют теплопроводность для этого состояния. Коэффициенты теплопроводности основных материалов, которые используются для утепления, приведены в таблице.
| Наименование материала | Коэффициент теплопроводности Вт/(м·°C) | ||
| В сухом состоянии | При нормальной влажности | При повышенной влажности | |
| Войлок шерстяной | 0,036-0,041 | 0,038-0,044 | 0,044-0,050 |
| Каменная минеральная вата 25-50 кг/м3 | 0,036 | 0,042 | 0,,045 |
| Каменная минеральная вата 40-60 кг/м3 | 0,035 | 0,041 | 0,044 |
| Каменная минеральная вата 80-125 кг/м3 | 0,036 | 0,042 | 0,045 |
| Каменная минеральная вата 140-175 кг/м3 | 0,037 | 0,043 | 0,0456 |
| Каменная минеральная вата 180 кг/м3 | 0,038 | 0,045 | 0,048 |
| Стекловата 15 кг/м3 | 0,046 | 0,049 | 0,055 |
| Стекловата 17 кг/м3 | 0,044 | 0,047 | 0,053 |
| Стекловата 20 кг/м3 | 0,04 | 0,043 | 0,048 |
| Стекловата 30 кг/м3 | 0,04 | 0,042 | 0,046 |
| Стекловата 35 кг/м3 | 0,039 | 0,041 | 0,046 |
| Стекловата 45 кг/м3 | 0,039 | 0,041 | 0,045 |
| Стекловата 60 кг/м3 | 0,038 | 0,040 | 0,045 |
| Стекловата 75 кг/м3 | 0,04 | 0,042 | 0,047 |
| Стекловата 85 кг/м3 | 0,044 | 0,046 | 0,050 |
| Пенополистирол (пенопласт, ППС) | 0,036-0,041 | 0,038-0,044 | 0,044-0,050 |
| Экструдированный пенополистирол (ЭППС, XPS) | 0,029 | 0,030 | 0,031 |
| Пенобетон, газобетон на цементном растворе, 600 кг/м3 | 0,14 | 0,22 | 0,26 |
| Пенобетон, газобетон на цементном растворе, 400 кг/м3 | 0,11 | 0,14 | 0,15 |
| Пенобетон, газобетон на известковом растворе, 600 кг/м3 | 0,15 | 0,28 | 0,34 |
| Пенобетон, газобетон на известковом растворе, 400 кг/м3 | 0,13 | 0,22 | 0,28 |
| Пеностекло, крошка, 100 — 150 кг/м3 | 0,043-0,06 | ||
| Пеностекло, крошка, 151 — 200 кг/м3 | 0,06-0,063 | ||
| Пеностекло, крошка, 201 — 250 кг/м3 | 0,066-0,073 | ||
| Пеностекло, крошка, 251 — 400 кг/м3 | 0,085-0,1 | ||
| Пеноблок 100 — 120 кг/м3 | 0,043-0,045 | ||
| Пеноблок 121- 170 кг/м3 | 0,05-0,062 | ||
| Пеноблок 171 — 220 кг/м3 | 0,057-0,063 | ||
| Пеноблок 221 — 270 кг/м3 | 0,073 | ||
| Эковата | 0,037-0,042 | ||
| Пенополиуретан (ППУ) 40 кг/м3 | 0,029 | 0,031 | 0,05 |
| Пенополиуретан (ППУ) 60 кг/м3 | 0,035 | 0,036 | 0,041 |
| Пенополиуретан (ППУ) 80 кг/м3 | 0,041 | 0,042 | 0,04 |
| Пенополиэтилен сшитый | 0,031-0,038 | ||
| Вакуум | |||
| Воздух +27°C. 1 атм | 0,026 | ||
| Ксенон | 0,0057 | ||
| Аргон | 0,0177 | ||
| Аэрогель (Aspen aerogels) | 0,014-0,021 | ||
| Шлаковата | 0,05 | ||
| Вермикулит | 0,064-0,074 | ||
| Вспененный каучук | 0,033 | ||
| Пробка листы 220 кг/м3 | 0,035 | ||
| Пробка листы 260 кг/м3 | 0,05 | ||
| Базальтовые маты, холсты | 0,03-0,04 | ||
| Пакля | 0,05 | ||
| Перлит, 200 кг/м3 | 0,05 | ||
| Перлит вспученный, 100 кг/м3 | 0,06 | ||
| Плиты льняные изоляционные, 250 кг/м3 | 0,054 | ||
| Полистиролбетон, 150-500 кг/м3 | 0,052-0,145 | ||
| Пробка гранулированная, 45 кг/м3 | 0,038 | ||
| Пробка минеральная на битумной основе, 270-350 кг/м3 | 0,076-0,096 | ||
| Пробковое покрытие для пола, 540 кг/м3 | 0,078 | ||
| Пробка техническая, 50 кг/м3 | 0,037 |
Часть информации взята нормативов, которые прописывают характеристики определенных материалов (СНиП 23-02-2003, СП 50.13330.2012, СНиП II-3-79* (приложение 2)). Те материал, которые не прописаны в стандартах, найдены на сайтах производителей
Так как стандартов нет, у разных производителей они могут значительно отличаться, потому при покупке обращайте внимание на характеристики каждого покупаемого материала
Закон теплопроводности Фурье
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
\vec{q}=-\varkappa\,\mathrm{grad}(T),
где \vec{q} — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, \varkappa — коэффициент теплопроводности
(удельная теплопроводность), T — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно какзакон теплопроводности Фурье .
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
P=-\varkappa\frac{S\Delta T}{l},
где P — полная мощность тепловых потерь, S — площадь сечения параллелепипеда, \Delta T — перепад температур граней, l — длина параллелепипеда, то есть расстояние между гранями.{2}} \sqrt{\frac{RT}{\mu}}
где i — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5, для одноатомного i=3), k — постоянная Больцмана, \mu — молярная масса, T — абсолютная температура, d — эффективный (газокинетический) диаметр молекул, R — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из нерадиоактивных газов — у ксенона).
Теплопроводность в сильно разреженных газах
Приведённое выше выражение для коэффициента теплопроводности в газах не зависит от давления. Однако если газ сильно разрежен, то длина свободного пробега определяется не столкновениями молекул друг с другом, а их столкновениями со стенками сосуда. Состояние газа, при котором длина свободного пробега молекул ограничивается размерами сосуда называют высоким вакуумом
. При высоком вакууме теплопроводность убывает пропорционально плотности вещества (то есть пропорциональна давлению в системе): \varkappa \sim \frac{1}{3}\rho c_v l \bar v\propto P, где l — размер сосуда, P — давление.
Таким образом коэффициент теплопроводности вакуума тем ближе к нулю, чем глубже вакуум. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, энергия в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотерь стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Экономичная штукатурная теплоизоляция.
Полимерные штукатурки можно только купить, их не изготовить самостоятельно. Но растворы на минеральных вяжущих экономичнее смешивать своими руками.
Заказать работу наемным рабочим дорого. Но, если смесь изготовить самостоятельно, общая цена несколько упадет. Многие застройщики экономят таким образом: нанимают штукатуров, а сами выполняют для них «черную» работу. С учетом того, что помощь подсобника оплачивается не за м2, а по дням, экономия может быть не значительной. Приблизительно 800-1200 руб/день.
Еще дешевле самостоятельная подготовка стены, выставление маяков и грубое оштукатуривание. «Спецам» останется только выровнять покрытие и нанести декоративный раствор.
Теплоизоляционная дешевая штукатурка для наружных работ.
Изолирующие смеси дороже обычных, поскольку сложнее. Своими руками, к тому же, можно сделать далеко не все.
Однако изготовление раствора на основе цемента под силам любому начинающему строителю и способно ощутимо снизить расход средств. В качестве наполнителя можно использовать как влагостойкие насыпные материалы (вспененное стекло, керамзитовые пески), так и не влагостойкое (опилки, перлит, вермикулит). Последние лишь защищают слоем плотного бетона.
Для внешней теплоизоляционной штукатурки возможно применение полистирольных наполнителей. Самый экономичный наполнитель – измельченный пенополистирол. Его стоимость нулевая, он бесплатен. Если использовать для измельчения пенопластовую упаковку.
Такой бетон широко применяется в России и за ее пределами. Он не плотен и не применим в конструкциях, требующих высокой прочности. Но для внешних утепляющих штукатурок вполне подходит.
Теплоизоляционная штукатурка своими руками для внутренних работ.
За квадратный метр отделки без наполнителя застройщики отдают меньше, чем за смесь с наполнителем. Поэтому некоторые, особенно «предприимчивые» строители, пытаются добавлять утепляющие подсыпки в готовые смеси. Это запрещено: такие манипуляции сильно ослабляют раствор, снижают его прочность и долговечность.
Чтобы снизить стоимость за кв. м. проще сделать замес самому, используя недорогие наполнители и вяжущее. Так глиняно-опилочный раствор практически бесплатен, хотя и не уступает по прочности гипсовому. data-matched-content-ui-type=»image_stacked» data-matched-content-rows-num=»2″ data-matched-content-columns-num=»3″ data-ad-format=»autorelaxed»>
Конвекция в атмосфере
Важность атмосферной конвекции велика, поскольку благодаря ней существуют такие явления, как ветры, циклоны, образование облаков, дожди и другие. Все эти процессы подчиняются физическим законам термодинамики
Среди процессов конвекции в атмосфере самым важным является круговорот воды. Здесь следует рассмотреть вопросы о том, что такое теплопроводность и теплоемкость воды. Под теплоемкостью воды понимается физическая величина, показывающая, какое количество теплоты необходимо передать 1 кг воды, чтобы ее температура увеличилась на один градус. Оно равно 4220 Дж.
Смотреть галерею
Круговорот воды осуществляется следующим образом: солнце нагревает воды Мирового океана, и часть воды испаряется в атмосферу. За счет процесса конвекции водяной пар поднимается на большую высоту, охлаждается, образуются облака и тучи, которые приводят к возникновению осадков в виде града или дождя.
Определение
Теплопроводностью материала называют перенос внутренней энергии от более нагретых частей к менее нагретым. Механизм переноса тепла отличается в зависимости от агрегатного состояния вещества, а также распределения температур по поверхности материала. Иными словами, способность тела проводить тепло — и есть теплопроводность. Определяется она количеством теплоты, которое способно проходить через определенную толщину материала, на определенном участке за обозначенное время (естественно, для удобства расчетов все показатели равны единице). Но штукатурки отличаются слоем нанесения — значит и показатель будет другим
Понятие теплопроводности на практике
Теплопроводность учитывается на этапе проектирования здания
При этом берется во внимание способность материалов удерживать тепло. Благодаря их правильному подбору жильцам внутри помещения всегда будет комфортно
Во время эксплуатации будут существенно экономиться денежные средства на отопление.
Утепление на стадии проектирования является оптимальным, но не единственным решением. Не составляет трудности утеплить уже готовое здание путем проведения внутренних или наружных работ. Толщина слоя изоляции будет зависеть от выбранных материалов. Отдельные из них (к примеру, дерево, пенобетон) могут в некоторых случаях использоваться без дополнительного слоя термоизоляции. Главное, чтобы их толщина превышала 50 сантиметров.
Особенное внимание следует уделить утеплению кровли, оконных и дверных проемов, пола. Сквозь эти элементы уходит больше всего тепла
Зрительно это можно увидеть на фотографии в начале статьи.
Что такое теплопроводность и термическое сопротивление
При выборе строительных материалов для строительства необходимо обращать внимание на характеристики материалов. Одна из ключевых позиций — теплопроводность
Она отображается коэффициентом теплопроводности. Это количество тепла, которое может провести тот или иной материал за единицу времени. То есть, чем меньше этот коэффициент, тем хуже материал проводит тепло. И наоборот, чем выше цифра, тем тепло отводится лучше.
Диаграмма, которая иллюстрирует разницу в теплопроводности материалов
Материалы с низкой теплопроводностью используются для утепления, с высокой — для переноса или отвода тепла. Например, радиаторы делают из алюминия, меди или стали, так как они хорошо передают тепло, то есть имеют высокий коэффициент теплопроводности. Для утепления используются материалы с низким коэффициентом теплопроводности — они лучше сохраняют тепло. В случае если объект состоит из нескольких слоев материала, его теплопроводность определяется как сумма коэффициентов всех материалов. При расчетах, рассчитывается теплопроводность каждой из составляющих «пирога», найденные величины суммируются. В общем получаем теплоизоляцонную способность ограждающей конструкции (стен, пола, потолка).
Теплопроводность строительных материалов показывает количество тепла, которое он пропускает за единицу времени
Есть еще такое понятие как тепловое сопротивление. Оно отображает способность материала препятствовать прохождению по нему тепла. То есть, это обратная величина по отношению к теплопроводности. И, если вы видите материал с высоким тепловым сопротивлением, его можно использовать для теплоизоляции. Примером теплоизоляционных материалов может случить популярная минеральная или базальтовая вата, пенопласт и т.д. Материалы с низким тепловых сопротивлением нужны для отведения или переноса тепла. Например, алюминиевые или стальные радиаторы используют для отопления, так как они хорошо отдают тепло.
Шаг 5: Правила монтажа
Стоит сказать, что все указанные выше показатели приведены для СУХИХ материалов. Если материл, намокнет, он потеряет свои свойства как минимум наполовину, а то и вовсе превратится в «тряпку». Поэтому нужно защищать теплоизоляцию. Пенопластом чаще всего утепляют под мокрый фасад, в котором утеплитель защищен слоем штукатурки. На минвату накладывается гидроизоляционная мембрана, чтобы не допустить попадание влаги.
Еще один момент, который заслуживает внимания — ветрозащита. Утеплители имеют разную пористость. Например, сравним плиты пенополистирола и минеральную вату. Если первый на вид выглядит цельным, на втором явно видны поры или волокна. Поэтому, если вы монтируете волокнистую теплоизоляцию, например, минвату или эковату на продуваемом ветром ограждении обязательно позаботьтесь о ветрозащите. В противном случае от хороших термических показателей утеплителя не будет пользы.
Как рассчитать толщину стен
Для того чтобы зимой в доме было тепло, а летом прохладно, необходимо чтобы ограждающие конструкции (стены, пол, потолок/кровля) должны иметь определенное тепловое сопротивление. Для каждого региона эта величина своя. Зависит она от средних температур и влажности в конкретной области.
Термическое сопротивление ограждающих конструкций для регионов России
Для того чтобы счета за отопление не были слишком большими, подбирать строительные материалы и их толщину надо так, чтобы их суммарное тепловое сопротивление было не меньше указанного в таблице.
Расчет толщины стены, толщины утеплителя, отделочных слоев
Для современного строительства характерна ситуация, когда стена имеет несколько слоев. Кроме несущей конструкции есть утепление, отделочные материалы. Каждый из слоев имеет свою толщину. Как определить толщину утеплителя? Расчет несложен. Исходят из формулы:
Формула расчета теплового сопротивления
R — термическое сопротивление;
p — толщина слоя в метрах;
k — коэффициент теплопроводности.
Предварительно надо определиться с материалами, которые вы будете использовать при строительстве. Причем, надо знать точно, какого вида будет материал стен, утепление, отделка и т.д. Ведь каждый из них вносит свою лепту в теплоизоляцию, и теплопроводность строительных материалов учитывается в расчете.
Сначала считается термическое сопротивление конструкционного материала (из которого будет строится стена, перекрытие и т.д.), затем «по остаточному» принципу подбирается толщина выбранного утеплителя. Можно еще принять в расчет теплоизоляционных характеристики отделочных материалов, но обычно они идут «плюсом» к основным. Так закладывается определенный запас «на всякий случай». Этот запас позволяет экономить на отоплении, что впоследствии положительно сказывается на бюджете.
Пример расчета толщины утеплителя
Разберем на примере. Собираемся строить стену из кирпича — в полтора кирпича, утеплять будем минеральной ватой. По таблице тепловое сопротивление стен для региона должно быть не меньше 3,5. Расчет для этой ситуации приведен ниже.
- Для начала просчитаем тепловое сопротивление стены из кирпича. Полтора кирпича это 38 см или 0,38 метра, коэффициент теплопроводности кладки из кирпича 0,56. Считаем по приведенной выше формуле: 0,38/0,56 = 0,68. Такое тепловое сопротивление имеет стена в 1,5 кирпича.
- Эту величину отнимаем от общего теплового сопротивления для региона: 3,5-0,68 = 2,82. Эту величину необходимо «добрать» теплоизоляцией и отделочными материалами.
Рассчитывать придется все ограждающие конструкции
- Считаем толщину минеральной ваты. Ее коэффициент теплопроводности 0,045. Толщина слоя будет: 2,82*0,045 = 0,1269 м или 12,7 см. То есть, чтобы обеспечить требуемый уровень утепления, толщина слоя минеральной ваты должна быть не меньше 13 см.
Если бюджет ограничен, минеральной ваты можно взять 10 см, а недостающее покроется отделочными материалами. Они ведь будут изнутри и снаружи. Но, если хотите, чтобы счета за отопление были минимальными, лучше отделку пускать «плюсом» к расчетной величине. Это ваш запас на время самых низких температур, так как нормы теплового сопротивления для ограждающих конструкций считаются по средней температуре за несколько лет, а зимы бывают аномально холодными
Потому теплопроводность строительных материалов, используемых для отделки просто не принимают во внимание
Коэффициент теплопроводности.
Количество тепла, которое проходит через стены (а по научному — интенсивность теплопередачи за счет теплопроводности) зависит от разности температур (в доме и на улице), от площади стен и теплопроводности материала, из которого сделаны эти стены.
Для количественной оценки теплопроводности существует коэффициент теплопроводности материалов. Этот коэффициент отражает свойство вещества проводить тепловую энергию. Чем больше значение коэффициента теплопроводности материала, тем лучше он проводит тепло. Если мы собираемся утеплять дом, то надо выбирать материалы с небольшим значением этого коэффициента. Чем он меньше, тем лучше. Сейчас в качестве материалов для утепления зданий наибольшее распространение получили утеплители из минеральной ваты, и различных пенопластов. Набирает популярность новый материал с улучшенными теплоизоляционными качествами — Неопор.
Коэффициент теплопроводности материалов обозначается буквой ? (греческая строчная буква лямбда) и выражается в Вт/(м2*К). Это означает, что если взять стену из кирпича, с коэффициентом теплопроводности 0,67 Вт/(м2*К), толщиной 1 метр и площадью 1 м2., то при разнице температур в 1 градус, через стену будет проходить 0,67 ватта тепловой энергии. Если разница температур будет 10 градусов, то будет проходить уже 6,7 ватта. А если при такой разнице температур стену сделать 10 см, то потери тепла будут уже 67 ватт. Подробней о методике расчета теплопотерь зданий можно посмотреть здесь.
Следует отметить, что значения коэффициента теплопроводности материалов указываются для толщины материала в 1 метр. Чтобы определить теплопроводность материала для любой другой толщины, надо коэффициент теплопроводности разделить на нужную толщину, выраженную в метрах.
В строительных нормах и расчетах часто используется понятие «тепловое сопротивление материала». Это величина обратная теплопроводности. Если, на пример, теплопроводность пенопласта толщиной 10 см — 0,37 Вт/(м2*К), то его тепловое сопротивление будет равно 1 / 0,37 Вт/(м2*К) = 2,7 (м2*К)/Вт.
Коэффициент теплопроводности — это… Что такое Коэффициент теплопроводности?
Теплопрово́дность — это перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.
Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.
В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры:
где — вектор потока тепла — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, — коэффициент теплопроводности (иногда называемый просто теплопроводностью), T — температура. Это выражение известно как закон теплопроводности Фурье.
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
где P — полная мощность тепловых потерь, S — площадь сечения параллелепипеда, ΔT — перепад температур граней, h — длина параллелепипеда, то есть расстояние между гранями.
Коэффициент теплопроводности измеряется в Вт/(м·K).
Коэффициенты теплопроводности различных веществ
| Материал | Теплопроводность, Вт/(м·K) |
|---|---|
| Алмаз | 1001—2600 |
| Серебро | 430 |
| Медь | 382—390 |
| Золото | 320 |
| Алюминий | 202—236 |
| Латунь | 97—111 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Сталь | 47 |
| Кварц | 8 |
| Стекло | 1 |
| Вода | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Пенобетон | 0,14—0,3 |
| Газобетон | 0,1—0,3 |
| Дерево | 0,15 |
| Шерсть | 0,05 |
| Минеральная вата | 0,045 |
| Пенополистирол | 0,04 |
| Пеноизол | 0,035 |
| Воздух (300 K, 100 кПа) | 0,026 |
| Воздух (сухой неподвижный) | 0,024—0,031 |
| Аргон | 0,0177 |
| Ксенон | 0,0057 |
| Аэрогель | 0,003 |
| Вакуум (абсолютный) | 0 (строго) |
На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы).
Коэффициент теплопроводности вакуума
Коэффициент теплопроводности вакуума стремится к нулю. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тепло в вакууме передаётся только излучением. Поэтому для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность хуже излучает и лучше отражает), а воздух между ними откачивают.
Связь с электропроводностью
Связь коэффициента теплопроводности K с удельной электрической проводимостью σ в металлах устанавливает закон Видемана — Франца:
где k — постоянная Больцмана, e — заряд электрона.
Обобщения закона Фурье
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. д. Инерционность в уравнения переноса первым ввел Максвелл[1], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[2]
Если время релаксации τ пренебрежимо мало, то это уравнение переходит в закон Фурье.
Примечания
- ↑ J. C. Maxwell, Philos. Trans. Roy. Soc. London 157 (1867) 49.
- ↑ C. Cattaneo, Atti Seminario Univ. Modena 3 (1948) 33.
См. также
Другие способы теплопередачи
Wikimedia Foundation. 2010.
Характеристики теплопередачи функционализированных нанопластинок графена Водные наножидкости
Материалы (Базель). 2016 июн; 9 (6): 455.
Давид Кабалейро
2 Departamento de Física Aplicada, Facultade de Ciencias, Universidade de Vigo, Виго E-36310, Испания; se.ogivu@orielabacad
Луис Луго
2 Departamento de Física Aplicada, Facultade de Ciencias, Universidade de Vigo, Виго E-36310, Испания; se.ogivu@orielabacad
Дипак Пант, академический редактор
2 Departamento de Física Aplicada, Facultade de Ciencias, Universidade de Vigo, Виго E-36310, Испания; se.ogivu @ orielabacadПоступило в редакцию 29 апреля 2016 г .; Принято 31 мая 2016 г.
Лицензиат MDPI, Базель, Швейцария. Эта статья представляет собой статью в открытом доступе, распространяемую в соответствии с условиями лицензии Creative Commons Attribution (CC-BY) (http://creativecommons.org/licenses/by/4.0/). Эта статья цитируется в других статьях в ЧВК.Abstract
Низкая теплопроводность жидкостей, используемых во многих промышленных приложениях, является одним из основных ограничений при разработке более эффективных систем теплопередачи.Перспективным решением этой проблемы является суспензия наночастиц с высокой теплопроводностью в базовой жидкости. Эти суспензии, известные как наножидкости, обладают большим потенциалом для улучшения теплопередачи. В данной работе рассматривается улучшение теплопередачи графеновых нанопластин, функционализированных сульфоновой кислотой, наножидкостей на водной основе. Для этого была разработана новая экспериментальная установка. Коэффициенты конвекции, перепады давления и теплофизические свойства различных наножидкостей при различных концентрациях были измерены для нескольких рабочих условий, и результаты сравниваются с результатами для чистой воды.Повышение теплопроводности и коэффициента конвективной теплопередачи достигает 12% (1 мас.%) И 32% (0,5 мас.%) Соответственно. Разработаны новые корреляции, позволяющие предсказывать число Нуссельта и коэффициент трения этого типа наножидкости в зависимости от других безразмерных величин. Кроме того, из экспериментальных данных коэффициента конвекции и перепада давления получают коэффициенты тепловых характеристик, чтобы оценить удобство замены базовой жидкости разработанными наножидкостями.
Ключевые слова: коэффициент теплопередачи , наножидкость, графеновые нанопластинки, перепад давления
1. Введение
Энергия — один из самых ценных ресурсов в нашем обществе, и поэтому в последние годы было приложено много усилий для того, чтобы повысить энергоэффективность и поощрять использование возобновляемых источников энергии. Широкий спектр применений, например, в области солнечной и геотермальной энергии, влечет за собой передачу тепловой энергии от одной жидкости к другой.Таким образом, управление теплом стало одной из областей с наибольшим потенциалом улучшения тепловых характеристик. Чтобы разработать более эффективное и компактное оборудование для теплопередачи, с середины двадцатого века возникло множество методов улучшения теплопередачи. Однако низкая теплопроводность жидкостей, обычно используемых в промышленности, таких как вода или гликоли, препятствует любому усилению теплопередачи. Чтобы преодолеть эту проблему, несколько авторов предложили использовать жидкости с улучшенными тепловыми свойствами.
Основываясь на том факте, что твердые тела обладают теплопроводностью на несколько порядков выше, чем обычные промышленные теплоносители, в последние десятилетия 20-го века некоторые исследователи предложили улучшить тепловые свойства жидкостей путем диспергирования твердых частиц миллиметрового и микрометрического размера с высокой проводимостью. . Несмотря на то, что теплопроводность этих смесей значительно улучшается с добавлением твердых частиц, эти дисперсии обладают множеством недостатков, ограничивающих их использование в промышленности.Некоторые из этих проблем — эрозия теплопередающего оборудования, осаждение твердых частиц или огромное увеличение перепада давления, связанное с более высокой вязкостью по сравнению с базовой жидкостью. Таким образом, добавление твердых частиц было отвергнуто как альтернатива повышения температуры до последних лет 20-го века, когда достижения в области материаловедения позволили крупномасштабное производство гораздо более мелких твердых частиц. В 1995 году Чой и Истман [1] возобновили предыдущие исследования увеличения теплопроводности за счет добавления нанометровых твердых частиц в базовые жидкости.Эти образцы, которые они назвали наножидкостями, имеют более высокую теплопроводность, чем исходные базовые жидкости, а также лишены проблем, связанных с дисперсиями с миллиметровыми и микрометрическими частицами. Благодаря небольшому размеру наночастиц системы теплопередачи не изнашиваются, и осаждение происходит намного медленнее. Более того, для малых концентраций наночастиц увеличение перепада давления незначительно по сравнению с перепадом давления базовой жидкости [2,3]. Количество экспериментальных исследований и публикаций, связанных с характеристиками теплопередачи наножидкостей, в последние годы экспоненциально увеличилось [4,5,6,7].Среди обычно используемых основных жидкостей вода — одна из самых распространенных в процессах теплообмена. По этой причине в последнее время было проведено множество исследований наножидкостей на водной основе [8,9,10].
Несмотря на то, что наножидкости представляют собой двухфазные системы (твердая и жидкая фазы), многие авторы, такие как Пак и Чо [11], Ксуан и Ли [7], а также Фард и другие. [12] соглашаются, что их поведение аналогично поведению чистого вещества с повышенными тепловыми свойствами. В данной работе исследуемые наножидкости рассматриваются как однофазные системы.Этот подход предполагает, что жидкая фаза и наночастицы находятся в тепловом равновесии и нет скольжения скорости между базовой жидкостью и твердыми частицами.
Наночастицы из различных материалов, таких как металлы, оксиды металлов и углеродные наноструктуры, были использованы для приготовления наножидкостей с улучшенными тепловыми свойствами для множества различных применений в таких областях, как теплотехника, возобновляемые источники энергии или медицина [13,14,15]. Двумерная структура графена в виде нанолиста толщиной в один атом из sp2-связанных атомов углерода, упакованных в сотовую решетку, демонстрирует более высокий потенциал, чем другие наноструктурированные углеродные аллотропы, такие как одномерные нанотрубки или нульмерные фуллерены [ 16].Таким образом, графен сочетает в себе преимущества высокоупорядоченного графитового углерода: высокую стабильность, обилие источника и низкую стоимость — с преимуществами однослойной теплопроводности в плоскости от 3000 до 5000 Вт · м −1 · K — 1 [16,17,18]. Хотя графен гидрофобен и, следовательно, не может диспергироваться в воде в течение длительного времени без агломерации [19], стабильные дисперсии в водных / органических растворителях могут быть получены после того, как материал будет функционализирован (с использованием кислотной обработки или аминофункции) с помощью следующих средств: правильной обработки ультразвуком [20,21,22].Ярманд и др. [22] заявил, что водные наножидкости на основе функционализированных нанопластинок графена и серебра (до 0,1 мас.%) Стабильны без помощи поверхностно-активных веществ или обработки ультразвуком.
Большинство исследований наножидкостей сосредоточено на анализе их физических свойств, как с экспериментальной, так и с теоретической точки зрения. Свойства, которые играют важную роль в конвективной теплопередаче, — это плотность, удельная теплоемкость, теплопроводность и вязкость.Хотя плотность и удельную теплоемкость можно легко предсказать с помощью теоретического подхода, теплопроводность и вязкость необходимо тщательно определять, потому что еще нет моделей, которые могут точно предсказать транспортные свойства наножидкостей [23,24]. За последние годы в литературе было опубликовано несколько исследований теплофизических характеристик и теплопередачи водных наножидкостей графеновых нанопластинок [22,25,26,27,28,29,30]. Однако большинство из них анализируют эффект добавления нанопластинок только при низких массовых концентрациях.Таким образом, что касается теплофизических характеристик, только Gupta et al. [25] и Hajjar et al. [26] достигала 0,25 мас.%, А Yu et al. [27] исследовали от 1 до 5 об.%.
Принудительная конвекция теплопередачи — это сложное явление, в котором сочетаются профили скорости и температуры, а также тепловые свойства жидкости. Ожидается значительное улучшение теплопередачи за счет добавления нанометровых частиц с высокой проводимостью. Увеличение эффективной теплопроводности жидкости — не единственный фактор, ускоряющий процесс теплопередачи [31].Присутствие этих твердых частиц также увеличивает колебания и турбулентность наножидкостей, дополнительно улучшая процесс теплопередачи. Увеличение турбулентности приводит к уменьшению градиентов температуры в жидкости и уменьшению толщины пограничных слоев там, где явления переноса протекают медленнее. Точно так же, благодаря небольшому размеру твердых частиц, увеличение падения давления по отношению к базовой жидкости минимально. Эти характеристики потока жидкости и теплопередачи наножидкостей также обсуждались Сюаном и Ли [9].Следовательно, больший энергообмен между жидкостью и твердыми стенками теплообменного оборудования может быть достигнут при той же потребляемой мощности накачки. По этой причине использование наножидкостей является одной из альтернатив с высоким потенциалом повышения энергоэффективности процессов теплопередачи. Одна из текущих тенденций состоит в изучении эффектов и потенциальных преимуществ применения магнитных полей в процессах теплопередачи с помощью наножидкостей [10,32,33,34,35,36].
Трудность, с которой сталкиваются при изучении наножидкостей, заключается в том, что обычные корреляции коэффициентов теплопередачи чистых веществ не могут предсказать их тепловое поведение, даже если в расчетах используются измеренные транспортные свойства наножидкостей. Об этой проблеме ранее сообщали, среди прочих, Сюань и Ли [9]. Это вызвано наличием движущихся твердых частиц, которые изменяют профили скорости и температуры потока по сравнению с профилями чистых веществ. Таким образом, новые корреляции, которые объясняют присутствие твердых частиц, должны быть исследованы, чтобы количественно описать тепловое поведение наножидкостей.
Целью данной статьи является исследование однофазного потока и термического поведения различных водных наножидкостей нанопластин графена, функционализированных сульфоновой кислотой, с экспериментальной точки зрения. Нанопластинки и наножидкости охарактеризованы теплофизически, и теплопередача за счет принудительной конвекции изучается для различных концентраций наночастиц с помощью нового устройства. Основные результаты обсуждаются и сравниваются с результатами, полученными для воды при тех же рабочих условиях, чтобы исследовать улучшение теплопередачи.Наконец, предлагаются новые корреляции для расчета числа Нуссельта и коэффициента трения Дарси для этого типа наножидкостей.
2. Характеристики наножидкостей
2.1. Материал и подготовка образцов
Графеновые нанопластинки (ЗНЧ) были предоставлены NanoInnova Technologies S.L. (Мадрид, Испания), тогда как воду Milli Q-Grade получали с удельным сопротивлением 18,2 МОм · см с помощью системы Millipore Milli-Q 185 Plus (Millipore Ltd., Уотфорд, Великобритания). Наножидкости были разработаны с помощью двухэтапного метода в виде дисперсий функционализированных сульфоновой кислотой графеновых нанопластинок с массовой концентрацией нанодобавок 0.25, 0,50, 0,75 и 1,00 мас.% В воде, что соответствует объемным долям 0,19, 0,39, 0,59 и 0,79 об.% Соответственно. Желаемые концентрации были получены путем взвешивания порошка в Mettler AE-200 (Mettler Toledo, Greifensee, Швейцария) с погрешностью 10 –4 г, а затем его перемешивания с заранее определенным объемом базовой жидкости в течение 120 мин. Затем суспензии обрабатывали ультразвуком в течение 240 мин с использованием ультразвуковой ванны (Ultrasounds, JP Selecta S.A., Барселона, Испания), работающей при частоте обработки ультразвуком 20 кГц с максимальной выходной мощностью 200 Вт.
2.2. Характеристика нанопорошка
Морфология сухого функционализированного сульфоновой кислотой нанопорошка графена была проанализирована с помощью сканирующей электронной микроскопии с использованием автоэмиссионного электронного микроскопа JEOL JSM-6700F (JEOL, Токио, Япония), работающего при напряжении ускорителя 20 кВ при обратном рассеянии. электронное изображение (детектор типа иттриевого алюминиевого граната). Это устройство соединено с энергодисперсионным рентгеновским (EDS) спектрометром Oxford Inca Energy 300 SEM (Oxford Instruments, Оксфорд, Великобритания), который также позволяет проводить химический микроанализ образца.Образцы SEM были приготовлены путем нанесения капли нанопорошка, диспергированного в метаноле аналитической чистоты (Sigma-Aldrich, Мадрид, Испания), на верхнюю часть подложки из диоксида кремния и сушки в атмосферных условиях. и показывают СЭМ-изображение и EDS-микроанализ исследуемого образца ЗНЧ соответственно. Графен, функционализированный сульфоновой кислотой, имеет форму нанопластинок размером до нескольких микрометров со складчатыми поверхностями, складывающимися по краям (). Спектр EDS показывает присутствие углерода (C), кислорода (O), серы (S) и кремнезема (Si), причем последнее связано с примесями физического носителя ().
СЭМ-изображение нанопластинок графена, функционализированных сульфоновой кислотой, при 3000-кратном увеличении.
Микроанализ EDS функционализированных сульфоновой кислотой графеновых нанопластинок: ( a ) исследуемая область; ( b ) Спектр ЭДС.
2.3. Теплофизические характеристики
Что касается теплофизических свойств базовой жидкости, были приняты во внимание значения из REFPROP [37]. Что касается сухого образца ЗНЧ, то в данной работе удельная теплоемкость была экспериментально определена с помощью квазиизотермического метода дифференциальной сканирующей калориметрии с температурной модуляцией (TDMSC) с использованием дифференциального сканирующего калориметра теплового потока, DSC, Q2000 (TA Instruments, New Castel, г. DE, США) [38].В противном случае использовалось значение плотности 1,27 г · см -3 для нанопорошка ЗНЧ. В данной работе плотности наножидкостей ЗНЧ ρ и удельная теплоемкость c p были получены с использованием следующих уравнений средневзвешенного значения [38]:
ρ n f = ϕ v × ρ G n P + (1 — ϕ v ) × ρ b f
(1)
c p nf = ϕ m × c p GnP + (1 — ϕ м ) × c p bf
(2)
где φ v — объемная доля нанодобавки, φ m — массовая доля нанодобавки, а индексы nf , GnP и bf обозначают наножидкость, графеновые нанопластинки и базовую жидкость, соответственно.Полученные значения плотности и удельной теплоемкости исследуемых флюидов в интервале температур от 20 до 40 ° C нанесены вместе с базовым флюидом в и соответственно. Плотность увеличивается с увеличением концентрации графена, тогда как для удельной теплоемкости происходит обратное. Изменения упомянутых свойств в отношении общих проанализированных условий базовой жидкости ниже 0,2% для ρ и 0,8% для c p .
Плотность функционализированных сульфоновой кислотой графеновых нанопластинок на водной основе, наножидкостей и воды [37].
Удельная теплоемкость функционализированных сульфоновой кислотой графеновых нанопластинок на водной основе, наножидкостей и воды [37].
Эффективные теплопроводности k были экспериментально измерены в этой работе от 20 до 40 ° C с помощью термоанализатора KD2 Pro (Decagon Devices, Inc., Pullman, WA, USA) вместе с зондом KS-1, равным 1,3. диаметр мм и длина 60 мм. Для точного контроля температуры образцы полностью погружали в масляную баню Grant GP200 (Grant Instruments, Кембридж, Великобритания).Более подробно об экспериментальной установке и методике измерений можно найти в предыдущих работах [39,40,41]. Температурная зависимость теплопроводности базовой жидкости и различных наножидкостей ЗНЧ показана на рис. Это свойство возрастает по мере увеличения концентрации нанопластинок, на 12% больше для наножидкости 1,00 мас.%, Чем для базовой жидкости.
Теплопроводность функционализированных сульфоновой кислотой графеновых нанопластинок на водной основе, наножидкостей и воды [37].
Наконец, динамическая вязкость образцов жидкости была определена в диапазоне температур от 20 до 40 ° C с использованием ротационного реометра Physica MCR 101 (Anton Paar, Грац, Австрия), оснащенного геометрией конус-пластина с углом конуса. 1 ° и диаметром 25 мм [2,41].И наножидкости, и базовая жидкость демонстрируют ньютоновское поведение в исследованном диапазоне концентраций. Полученные значения представлены в зависимости от температуры, где можно увидеть заметное увеличение вязкости с массовой концентрацией.
Вязкость функционализированных сульфоновой кислотой графеновых нанопластинок на водной основе, наножидкостей и воды [37].
3. Определение коэффициента теплопередачи
3.1. Экспериментальное оборудование
Новая экспериментальная установка состоит из двух замкнутых контуров, использующих тестируемую жидкость и горячую воду в качестве рабочих жидкостей, и открытого холодильного контура.Схема экспериментального оборудования и расположение используемых устройств показаны на рис. Основная часть экспериментальной установки, где изучаются теплообмен и перепад давления, состоит из теплообменника типа труба в трубе из нержавеющей стали длиной 930 мм и 1180 мм для опытных участков эффективного нагрева и перепада давления соответственно. Испытуемая жидкость прокачивается через внутреннюю трубу и нагревается горячей водой из другого замкнутого контура, которая течет внутри кольцевой секции.Внутренняя трубка имеет внутренний диаметр 8 мм и внешний диаметр 10 мм, а внешняя трубка имеет внутренний диаметр 15 мм. Испытательная секция была изолирована, чтобы минимизировать потери тепла в окружающую среду, которые, по оценкам, составляют менее 0,5% от общей теплопередачи даже для самых неблагоприятных условий эксплуатации. Таким образом, теплообменник можно считать адиабатическим, что значительно упрощает анализ.
Схема экспериментальной установки для определения коэффициентов теплоотдачи и перепада давления.
Горячая вода хранится в резервуаре емкостью 25 л, который обеспечивает тепловую инерцию контура и прокачивается через электрический нагреватель мощностью 4,5 кВт перед тем, как попасть в кольцевую секцию. Аналогичным образом тестируемая жидкость перекачивается из резервуара объемом 3 л в пластинчатый теплообменник, где она передает энергию охлаждающей воде. Затем эта испытанная жидкость течет в теплообменник «труба в трубе», где получает энергию от горячей воды. Холодильный контур состоит из резервуара, в котором хранится водопроводная вода перед тем, как ее прокачать через пластинчатый теплообменник для охлаждения испытуемой жидкости.
Расходы горячей воды и испытуемой жидкости регулируются как с помощью клапанов, так и регулируют скорость вращения центробежных насосов с помощью пропорционально-интегрально-производных (PID) регуляторов. Температура горячей воды также регулируется автоматически с помощью ПИД-регулятора, который регулирует электрическую мощность, подаваемую регулятором мощности на электрический нагреватель. Расход охлаждающей воды и, следовательно, температура тестируемой жидкости регулируется вручную с помощью игольчатого клапана.
Температуры горячей воды и испытуемой жидкости на входе и выходе из испытательной секции измеряются четырьмя резистивными датчиками температуры класса Pt100 A. Расход обеих жидкостей измеряется двумя разными электромагнитными расходомерами. Падение давления исследуемой жидкости через теплообменник типа труба в трубе измеряется датчиком перепада давления. Наконец, экспериментальная установка оснащена системой сбора данных, основанной на 16-битной карте сбора данных и ПК, где измеренные переменные отображаются в реальном времени и сохраняются в электронной таблице.
3.2. Экспериментальная процедура
С целью оценки увеличения коэффициентов конвективной теплопередачи и падения давления нескольких водных наножидкостей нанопластинок графена, функционализированных сульфоновой кислотой, было экспериментально проведено сравнение этих результатов с результатами, полученными для чистой воды. Таким образом, было проведено несколько наборов тестов для наножидкостей с массовой концентрацией графеновых нанопластинок 0,25%, 0,50%, 0,75% и 1,00%, а также для чистой воды.Каждое испытание определяется через значения объемного расхода и средней температуры в теплообменнике каждой жидкости.
Испытания теплопередачи проводились путем перекачивания исследуемой жидкости при различных расходах, при этом средняя температура горячей воды и испытуемой жидкости, а также расход горячей воды поддерживались постоянными. Пары исследуемых средних температур по отношению к исследуемой жидкости / горячей воде составляли по Цельсию 20/40, 30/40, 30/45, 30/50 и 40/60, а изучаемый расход жидкости находился в диапазоне от 200 до 700 л / ч с шагом 100 л / ч.Расход горячей воды был установлен на 800 л / ч для всех тестов. Расход воды был выбран как можно меньшим для достижения высокого перепада температур по теплообменнику, но достаточно высоким для обеспечения турбулентного режима (Re> 10 4 ). Это было сделано для расчета коэффициента теплопередачи на водяной стороне с использованием общепринятых соотношений для принудительной конвекции через кольцевые секции. Для оценки достоверности экспериментальных измерений коэффициенты конвективной теплоотдачи для чистой воды сравнивались со значениями, предсказанными известными корреляциями Гниелинского [42].Отклонения были менее 10% для всех тестируемых условий.
Испытания на падение давления также проводились при поддержании постоянной температуры испытуемой жидкости и перекачивании при различных расходах. Два испытания были проведены для средних температур 25 ° C и 35 ° C, и скорость потока варьировалась от 250 до 700 л · ч -1 с шагом 50 л · ч -1 шагов. Отклонения измеренных перепадов давления и рассчитанных на основе корреляций Гниелинского [42] также были менее 10%, обнаружив несколько более высокие отклонения для самых низких расходов.
4. Анализ данных
Теплопередача графеновых наножидкостей на водной основе может быть количественно описана с помощью коэффициента конвективной теплопередачи. Коэффициенты конвекции различных наножидкостей сравниваются с коэффициентами чистой воды для анализа улучшения теплопередачи. Аналогичным образом сравниваются перепады давления наножидкостей и чистой воды.
Коэффициент конвекции не может быть измерен напрямую, но может быть рассчитан на основе измеренных данных следующим образом.Температуры испытуемой жидкости и греющей воды на входе и выходе из испытательной секции ( T tf в , T tf out , T hw в и T hw out ) были измерены экспериментально. Средняя логарифмическая разница температур ( LMTD ), обычно используемая в теплообменниках для описания движущей силы температуры, определяется как:
LMTD = (Thwin − Ttfout) — (Thwout − Ttfin) ln (Thwin − TtfoutThwout − Ttfin)
(3)
Общее тепловое сопротивление в испытательной секции, R ov , было получено как частное (LMTD) и расхода тепла на стороне горячей воды (Q˙) в соответствии со следующим уравнением:
где Q˙ определяется как:
Q˙ = ρhw × cphw × V˙hw × (Thwin − Thwout)
(5)
где V˙ hw — объемный расход горячей воды, а ρ hw и c p hw — ее плотность и удельная теплоемкость соответственно.Расчеты проводились с использованием теплового потока на стороне горячей воды, уравнение (5), поскольку неопределенности свойств воды ниже, чем у наножидкостей.
Общее тепловое сопротивление складывается из теплового сопротивления, соответствующего внешней принудительной конвекции ( R hw ), теплопроводного теплового сопротивления стальной трубы ( R s ) и внутренней принудительной конвекции. сопротивление ( R тс ).В этой работе предполагалось, что сопротивление загрязнению будет незначительным, поскольку перед экспериментами использованная трубка была очищена. Следовательно, тепловое сопротивление на стороне испытуемой жидкости можно рассчитать с помощью следующего уравнения:
R t f = R o v — R s — R h w
(6 )
Тепловое сопротивление конвекции на стороне горячей воды определяется уравнением:
R h w = ( π × d 2 × L h × h h w ) −1
(7)
где d 2 соответствует внешнему диаметру внутренней трубы, а L h — эффективная длина нагрева испытательной секции.Коэффициент теплопередачи h hw был рассчитан с использованием корреляций, предложенных Гниелински [42] для полностью развитых турбулентных течений в кольцевых каналах с адиабатическими внешними поверхностями. Эти отношения задаются:
h h w = k h w × N u h w / d h
(8)
N u h w = ψ × N u ∗ h w
(9)
ψ = 0.75 × a −0,17
(10)
Nu ∗ w = (fhw / 8) × Rehw × Prhw × (1+ (dh / Lh) 2/3) ω + 12,7 × (fhw / 8 ) 1/2 × (Prhw2 / 3−1)
(12)
ω = 1,07 + 900 × Rehw − 1−0,63 × (1 + 10 × Prhw) −1
(13)
f h w = (0,782 × ln (Re ∗ h w ) −1,50) −2
(14)
Re ∗ hw = (1 + a2) × ln (a) + (1 − a2) (1 − a) 2 × ln (a) × Rehw
(15)
где d h , гидравлический диаметр кольцевого сечения, представляет собой внутренний диаметр внешней трубы, d 3 , минус внешний диаметр внутренней трубы, d 2 ; и k hw — теплопроводность горячей воды.Число Нуссельта ( Nu hw ), число Рейнольдса (Re hw ) и число Прандтля (Pr hw ) горячей воды были рассчитаны в соответствии с их обычными определениями. Теплофизические и транспортные свойства горячей воды были получены из REFPROP [37] с учетом того, что вода является насыщенной жидкостью при средней температуре между входом и выходом.
С другой стороны, проводящее тепловое сопротивление, R s , было рассчитано с учетом одномерного теплообмена в радиальном направлении и в соответствии с уравнением:
Rs = ln (d2 / d1) 2π × ks × Lh
(16)
где d 1 — внутренний диаметр внутренней трубы теплообменника, изготовленной из нержавеющей стали AISI 316L.Его теплопроводность ( k s ) была рассчитана с использованием уравнения, предложенного Чунгом [43]:
к с = 9,248 + 0,01571 × ( T + 273,15)
(17)
где температура трубки T должна быть выражена в градусах Цельсия, а проводимость — в Вт · м −1 · K −1 . Температура трубки для каждого теста считалась постоянной, определяемой по формуле:
T = ¼ × ( T t f i n + T t f o u t + T h w i n + T h w o u t )
(18)
Следовательно, после того, как внутреннее тепловое сопротивление, R tf , вызванное конвекцией, было рассчитано с использованием уравнения (6), коэффициент конвекции был определен прямым способом с использованием следующего уравнения:
h t f = π × d 1 × L h × R t f −1
(19)
С другой стороны, падение давления исследуемой жидкости было измерено напрямую, и никакого дополнительного анализа для сравнения результатов для различных наножидкостей и воды не требуется.
Коэффициент теплопередачи и перепад давления являются размерными переменными, и, хотя они могут быть удобны для сравнения теплового и гидродинамического поведения наножидкостей, они не подходят для корреляции экспериментальных данных. Вместо этого можно использовать безразмерные группы для корреляции теплопередачи и падения давления с параметрами потока, а также свойствами и составом наножидкости.
Число Нуссельта для испытуемой жидкости ( Nu tf ) представляет собой безразмерную форму коэффициента конвекции испытуемой жидкости ( h tf ) и определяется следующим уравнением:
Аналогичным образом коэффициент трения Дарси исследуемой жидкости ( f tf ), который представляет безразмерный перепад давления в теплообменнике, определяется как:
футс = d1Lp × Δptfρtf × vtf2 / 2
(21)
где L p — эффективная длина падения давления в испытательной секции, а Δp tf , ρ tf и v tf — падение давления, плотность и средняя скорость. исследуемой жидкости соответственно.
В этой работе число Нуссельта тестируемой жидкости ( Nu tf ) было связано с ее числом Рейнольдса (Re tf ), числом Прандтля, оцененным при температуре в объеме (Pr tf ). ), Число Прандтля, оцененное при температуре стенки (Pr , стенка ) и объемной концентрации наночастиц ( φ v ). В данной работе предлагается следующее уравнение для корреляции экспериментальных данных теплопередачи для тестируемых жидкостей:
Nutf = c1 × (1 + c2 × ϕv) c3 × Retfc4 × Prtfc5 × (Prtf / Prwall) c6
(22)
Число Прандтля, Pr стена , у стены включено в корреляция для учета влияния теплопередачи на температурный профиль и так далее на тепловые свойства.Температура у стены считалась постоянной величиной:
Twall = 12 × (Ttfin + Ttfout) + Rtf × Q˙
(23)
Следует отметить, что объемная концентрация наночастиц использовалась для корреляции экспериментальных данных. Это связано с тем, что реологическое поведение суспензий, таких как наножидкости, сильно зависит от гидродинамических сил, которые действуют на поверхности частиц; поэтому предпочтительным является геометрический способ описания концентрации жидкости.Это обычная практика при изучении наножидкостей, о чем также говорили Пак и Чо [11].
Аналогичным образом коэффициент трения Дарси тестируемой жидкости ( f tf ) был связан с числом Рейнольдса и объемной концентрацией нанодобавок. Предлагаемое функциональное соотношение для коэффициента трения следует выражению:
ftf = c7 × (1 + c8 × ϕv) c9 × Retfc10
(24)
Для дальнейшей оценки тепловых характеристик сравнение чисел Нуссельта двух жидкостей должно быть уравновешено факторами трения, которые находятся под влиянием дисперсии наночастиц.Возможным средством оценки тепловой эффективности различных тестируемых наножидкостей является использование коэффициента тепловых характеристик, определяемого следующим соотношением [44,45]:
η t f = ( N u t f / N u b f ) × ( f т f / f b f ) 1/3
(25)
где f — коэффициент трения Дарси, Nu — число Нуссельта, а tf и bf обозначают тестируемую и базовую жидкости, соответственно.Результаты экспериментов были проанализированы с использованием этого параметра для сравнения тепловых характеристик различных наножидкостей.
Требуемые теплофизические свойства исследуемой жидкости, оцененные при средней температуре в теплообменнике, были получены из вышеупомянутых экспериментальных значений. Тщательный анализ неопределенности измеренных и рассчитанных величин был выполнен в соответствии с рекомендациями «Руководства по выражению неопределенности измерений (GUM)» [46].Результаты этого анализа подведены позже.
5. Результаты
Во-первых, коэффициенты теплопередачи и потери давления различных наножидкостей сравниваются и обсуждаются в связи с результатами по воде. После этого полученные численные значения корреляций числа Нуссельта и коэффициента трения Дарси представляются вместе с диапазонами их применимости. Кроме того, обсуждается анализ коэффициента тепловых характеристик как функции массовой концентрации.
5.1. Характеристики теплопередачи
Экспериментальные результаты для анализируемых наножидкостей на водной основе нанопластинок графена, функционализированных сульфоновой кислотой, показаны в качестве примера некоторых из многочисленных тестов. Отображаемое поведение является репрезентативным для остальных выполненных тестов, тенденция данных аналогична всем другим тестам.
5.1.1. Коэффициенты теплопередачи
Экспериментальные коэффициенты теплопередачи различных проанализированных наножидкостей и чистой воды в тестах 20 ° C / 40 ° C при разных скоростях потока представлены на графике как функция массовой концентрации графеновых нанопластинок при разных скоростях потока.Как и следовало ожидать, коэффициенты теплопередачи увеличиваются с увеличением расхода из-за увеличения перемешивания и турбулентности. Коэффициенты теплопередачи для испытаний 300 л · ч −1 при различных температурах представлены на графике. Каждая кривая представляет значения, измеренные при различных средних температурах тестируемой жидкости, при 20 ° C в качестве теплообменника LMTD. Как можно заметить, коэффициент теплопередачи выше при повышении температуры наножидкости, что согласуется с уменьшением вязкости исследуемой жидкости и увеличением ее теплопроводности.
Коэффициент теплопередачи в зависимости от концентрации графеновых нанопластинок при различных скоростях потока. Средняя температура тестируемой жидкости / горячей воды составляет 20 ° C / 40 ° C.
Коэффициент теплопередачи в зависимости от концентрации графеновых нанопластинок при различных температурах с расходом 300 л · ч −1 . LMTD в теплообменнике составляет 20 ° C.
При дальнейшем рассмотрении и видно, что коэффициенты теплоотдачи имеют плавную зависимость от концентрации графеновых нанопластинок.Теплопередача, достигаемая с наножидкостью 0,25%, выше, чем у чистой воды, и результаты были даже лучше, когда концентрация составляла 0,50%. Однако улучшение теплопередачи, полученное с 0,75% наножидкости, было меньше, а коэффициенты теплопередачи для массовой концентрации 1,00% были даже хуже, чем у чистой воды при многих условиях. Это может быть связано с тем, что при низких концентрациях наночастиц улучшение теплопередачи за счет теплопроводности и повышенная степень перемешивания более важны, чем штраф, вызванный увеличением эффективной вязкости наножидкости.Тем не менее, при более высоких концентрациях увеличение вязкости из-за присутствия твердых частиц преобладает над двумя другими эффектами, и в результате теплопередача снижается по сравнению с базовой жидкостью. Это говорит о существовании оптимальной концентрации наночастиц для данного набора рабочих условий. Полученные относительные улучшения теплопередачи по отношению к воде для каждой наножидкости (минимальные, средние и максимальные) суммированы в.
Таблица 1
Улучшение теплопередачи по отношению к воде для водных наножидкостей функционализированных графеновых нанопластинок.
| Nanofluid | Минимум | Среднее значение | Максимум | ||||
|---|---|---|---|---|---|---|---|
| φ м = 0,25% | -1,7% | 6,5% | 6,5% | 6,5% | м = 0,50%0,94% | 15,0% | 32,4% |
| φ м = 0,75% | −2,3% | 7,0% | 22,8% | м = 1.00% | −19,6% | –10,1% | 4,0% |
Что касается улучшения теплопередачи, отметим, что Садегинежад et al. [28] получил увеличение числа Нуссельта до 83% для наножидкостей нанопластинок графена при 0,1 мас.% В условиях турбулентной принудительной конвекции через простую трубку из нержавеющей стали. Ярманд и др. [29] количественно определил максимальное увеличение числа Нуссельта на 26,5%, используя квадратную трубку из нержавеющей стали для образцов при 0.1% масс.
5.1.2. Потери давления
Чтобы определить, подходит ли этот вид наножидкости для теплопередачи, необходимо также проанализировать падение давления, вызванное присутствием твердых частиц. В качестве примера показаны измерения падения давления наножидкостей 0,25%, 0,50% и 0,75%, а также чистой воды для различных скоростей потока и при температуре испытательной жидкости 35 ° C. Как и ожидалось, потери давления увеличиваются с увеличением расхода.Более того, как видно на этом рисунке, перепад давления немного увеличивается с увеличением массовой концентрации. Это увеличение может быть связано с более высокой вязкостью наножидкости, и по мере увеличения концентрации графена этот эффект становится более значительным, и потери давления растут.
Падение давления по сравнению с концентрацией графеновых нанопластинок при температуре испытательной жидкости 35 ° C и различных скоростях потока.
С учетом всех проведенных тестов также было обнаружено, что при более низкой температуре наножидкости, т.е.g., 25 ° C, потери давления были немного выше из-за более высокой вязкости. Относительное экспериментальное увеличение давления по отношению к чистой воде для каждой наножидкости (минимальное, среднее и максимальное) суммировано в.
Таблица 2
Относительное падение давления по отношению к чистой воде для наножидкостей на водной основе нанопластинок графена.
| Nanofluid | Минимум | Среднее значение | Максимум |
|---|---|---|---|
| φ м = 0.25% | 0,92% | 14,5% | 55,4% |
| φ м = 0,50% | 4,11% | 17,1% | 56,9% |
| 0,75% | 13,0% | 28,0% | 73,4% |
Эти результаты согласуются с результатами Садегинежада et al. [28], которые обнаружили максимальное увеличение перепада давления на 14,6% на 0,1 мас.%.
5.2. Безразмерный анализ
В литературе доступно множество корреляций для расчета числа Нуссельта и коэффициента трения Дарси для внутренней принудительной конвекции в воздуховодах круглого сечения. Однако эти корреляции были получены с использованием измерений чистых веществ и не могут предсказывать поведение наножидкостей. В этой работе были разработаны две новые корреляции, подходящие для расчета числа Нуссельта и коэффициента трения Дарси графеновых наножидкостей, функционализированных сульфоновой кислотой.
5.2.1. Корреляция чисел Нуссельта
Подгоночные коэффициенты c 1 — c 6 в уравнении (22) были определены с использованием регрессионного анализа наименьших квадратов. Предлагаемая корреляция для числа Нуссельта и диапазоны его применимости задаются следующими уравнениями:
Nunf = 0,011 × (1 + 100 × ϕv) −0,095 × Renf0,886 × Prnf0,545 × (Prnf / Prwall) −0,495
(26)
0,19 % ≤ ϕ v ≤ 0.79 %
(27)
5 × 10 3 ≤ Re n f ≤ 4 × 10 4
(28)
4.8 ≤ Pr n f ≤ 10,8
(29)
1,06 ≤ Pr n f / Pr w a l l ≤ 1,36
(30)
Должно быть отметили, что коэффициент Pr nf / Pr wall , который используется для учета влияния теплопередачи на температурный профиль, отличается, если жидкость нагревается или охлаждается.Во время всех испытаний тепло передавалось от горячей воды к наножидкости, и, следовательно, корреляция, заданная уравнением (26), должна использоваться только при нагревании наножидкости. Неопределенность экспериментального числа Нуссельта была оценена, и она составляла от 6% до 12% для всех измеренных значений. Отклонение между коррелированными числами Нуссельта и числами, измеренными экспериментально, составляет 13,2% для наихудшего случая (наножидкость с массовой концентрацией 0,25%, 40 ° C / 60 ° C и 700 л · ч -1 ) и составляет менее 10% и 8% для 90% и 75% измеренных значений соответственно.
5.2.2. Корреляция коэффициента трения Дарси
Процедура корреляции коэффициента трения была аналогична процедуре для числа Нуссельта. Полученные параметры подгонки от c 7 до c 10 в уравнении (24):
fnf = 0,109 × (1 + 100 × ϕv) 0,215 × Renf − 0,159
(31)
0,19 % ≤ ϕ v ≤ 0,59 %
(32)
8 × 10 3 ≤ Re n f ≤ 3.7 × 10 4
(33)
Анализ неопределенности экспериментального коэффициента трения приводит к значениям ниже 2% для всех измеренных значений. Отклонение между коррелированными коэффициентами трения Дарси и экспериментально измеренными составляет 4,7% для наихудшего случая (наножидкость с массовой концентрацией 0,75%, 35 ° C и 300 л · ч -1 ) и составляет менее 2,5% и 2% для 90% и 75% от измеренных значений соответственно.
5.2.3. Коэффициент тепловых характеристик
Анализ коэффициента тепловых характеристик, полученных для каждой массовой концентрации графеновых нанопластинок, был проведен путем объединения результатов различных тестов, собранных для разных скоростей потока.
Коэффициент тепловых характеристик в зависимости от концентрации графеновых нанопластинок при 30 ° C, с LMTD 10 ° C между жидкостями, для различных скоростей потока.
Для проведения этого сравнения была выбрана эталонная температура 30 ° C для обоих экспериментов. Таким образом, числа Нуссельта были получены в результате испытания теплопередачи 30 ° C / 40 ° C (средняя температура испытуемой жидкости при 30 ° C), в то время как коэффициенты трения были получены путем интерполяции испытаний на падение давления при 25 ° C и 35 ° C. .Как можно видеть на фиг. 5, коэффициент тепловых характеристик повышается, когда скорость потока увеличивается, и все наножидкости имеют благоприятные соотношения, за исключением 1 мас.%. Концентрационная зависимость этого фактора показывает максимальные значения при концентрации 0,5% по массе, достигая значения 1,27 для максимального расхода. В соответствии с предыдущими результатами, образец 1% показывает наихудшие результаты с коэффициентами тепловых характеристик ниже единицы для всех проанализированных скоростей потока.
6. Выводы
В данной работе было реализовано новое экспериментальное устройство для определения коэффициентов теплопередачи и перепада давления нескольких функционализированных сульфоновой кислотой графеновых наножидкостей в воде с концентрацией до 1 мас.% (0.79 об.%). Реометр, метод переходной горячей проволоки и дифференциальный сканирующий калориметр использовались для измерения вязкости, теплопроводности и теплоемкости анализируемых образцов, соответственно. Повышение теплопроводности достигает 12% для максимальной анализируемой концентрации.
Заметное улучшение коэффициентов конвекции, h tf , достигается для всех наножидкостей, кроме 1 мас.%. Эти коэффициенты увеличиваются с увеличением расхода и температуры жидкости.Зависимость от массовой концентрации показывает оптимальное значение 0,5%, для которого значения h tf на 32% выше, чем для воды. Потери давления монотонно увеличиваются с увеличением концентрации наночастиц из-за вязкости исследуемой жидкости.
Представлены две новые корреляции, способные описать число Нуссельта и коэффициент трения такой дисперсии как функцию безразмерных чисел. Отклонения менее 13,2% в случае Нуссельта и 4.Получены 7% потерь давления. Более того, коэффициент теплопередачи и результаты падения давления были объединены через коэффициент тепловых характеристик, чтобы оценить, будет ли выгодна замена базовой жидкости на наножидкости другой конструкции. Было обнаружено, что наножидкость 0,5% показывает наилучшие результаты, достигая увеличения этого фактора до 27%. Следовательно, использование наножидкостей является альтернативой с высоким потенциалом улучшения теплопередачи, учитывая, что при соответствующей концентрации графеновых нанопластинок можно добиться значительного улучшения коэффициентов теплопередачи при небольшом увеличении перепада давления.
Использование наножидкостей позволило бы разработать более эффективное и компактное оборудование для теплопередачи. Это может иметь особенно важное значение в технологиях возобновляемой и чистой энергии с потенциально интересным применением в области солнечной и геотермальной энергии. Этот тип нового материала может привести к уменьшению разницы температур между жидкостями, увеличению эффективности теплового оборудования или уменьшению требуемых расходов, что снизило бы потребление энергии насосом.Однако область наножидкостей все еще находится на начальной стадии, и необходимо провести новые работы, как теоретические, так и экспериментальные, чтобы понять и уметь предсказать их поведение.
Благодарности
Авторы выражают признательность за порошок функционализированных графеновых нанопластинок, предоставленный Nanoinnova Technologies S.L. (http://www.nanoinnova.com/Product). Эта работа была поддержана Министерством экономики и конкуренции (Испания) и программой FEDER в рамках проектов ENE2012-32908 и ENE2014-55489-C2-2-R.Давид Кабалейро выражает признательность Министерству образования, культуры и депортации (Испания) за финансовую поддержку программы FPU, а Хавьер П. Вальехо выражает признательность программе FPI «Министерио де Экономиа и конкуренция».
Сокращения
| Номенклатура | ||
| a | Отношение диаметров кольца, безразмерное | |
| c i | Константа корреляционного фитинга 4 c безразмерная 908 | Удельная теплоемкость, Дж · кг −1 · K −1 |
| d 1 | Внутренний диаметр внутренней трубы, м | |
| d 2 | Наружный диаметр внутренней трубы, м | |
| d 3 | Внутренний диаметр внешней трубы, м | |
| d h | Гидравлический диаметр, м | |
| f | Коэффициент трения Дарси, безразмерный | |
| h | Конвекция co эффективный, Вт · м −2 · K −1 | |
| k | Теплопроводность, Вт · м −1 · K −1 | |
| LMTD 74 | Logarith62 средняя разница температур, ° C | |
| L h | Эффективная длина нагрева, м | |
| L p | Эффективная длина падения давления, м | |
| Nu | Nus , безразмерный | |
| Pr | Число Прандтля, безразмерный | |
| Q˙ | Расход тепла, Вт | |
| R | Термическое сопротивление, К · Вт −1 | Число Рейнольдса, безразмерное |
| T | Температура, К, ° C | |
| v | Средняя скорость жидкость, м · с −1 | |
| V˙ | Объемный расход, м 3 · с −1 | |
| об.% | Объемная концентрация графеновых нанопластинок в процентах, безразмерная | |
| мас.% | Процентная массовая концентрация графеновых нанопластинок, безразмерная | |
| Δp | Падение давления, Па | |
| η | Коэффициент тепловых характеристик, безразмерный | 62кг · м −3 |
| φ м | Массовая концентрация графеновых нанопластинок, безразмерная | |
| φ v | Объемная концентрация графеновых нанопластинок, безразмерная | 900 | ωПоправочные коэффициенты для числа Нуссельта в кольцевом пространстве, безразмерные |
| Нижние индексы | ||
| bf | Базовая жидкость | |
| hw 3 | вВход в тестовую часть | |
| нф | Наножидкость | |
| вне | Выход из тестовой части | |
| ov | 911Сталь | |
| tf | Тестируемая жидкость | |
| w | Вода | |
| стенка | Трубная стенка | |
АвторПардиняс участвовал в реализации экспериментальной установки для разработки тестов теплопередачи, Роберто Агромайор определил экспериментальные коэффициенты теплопередачи и перепады давления наножидкостей, а Дэвид Кабалейро выполнил дизайн наножидкостей и их теплофизические характеристики. Роберто Агромайор, Анхель Б. Пардиньяс, Дэвид Кабалейро и Хавьер П. Вальехо проанализировали данные и написали статью. Хосе Фернандес-Сеара и Луис Луго придумали исследование, разработали его дизайн и координировали редактирование рукописи.Все авторы прочитали и одобрили окончательную рукопись.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов. Спонсоры-основатели не играли никакой роли в разработке исследования; при сборе, анализе или интерпретации данных; в написании рукописи и в решении опубликовать результаты.
Ссылки
1. Choi S.U.S., Eastman J.A. Повышение теплопроводности жидкостей с помощью наночастиц. КОРМИЛИ. 1995; 231: 99–105. [Google Scholar] 2.Кабалейро Д., Пасториса-Гальего М.Дж., Грасиа-Фернандес К., Пиньейро М.М., Луго Л. Реологические и объемные свойства наножидкостей TiO 2 -этиленгликоль. Nanoscale Res. Lett. 2013; 8: 1–13. DOI: 10.1186 / 1556-276X-8-286. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] 3. Шарма А.К., Тивари А.К., Диксит А.Р. Реологическое поведение наножидкостей: обзор. Обновить. Поддерживать. Energy Rev.2016; 53: 779–791. DOI: 10.1016 / j.rser.2015.09.033. [CrossRef] [Google Scholar] 4. Хуминик Г., Хуминик А.Применение наножидкостей в теплообменниках: обзор. Обновить. Поддерживать. Energy Rev.2012; 16: 5625–5638. DOI: 10.1016 / j.rser.2012.05.023. [CrossRef] [Google Scholar] 5. Трисаксри В., Вонгвизес С. Критический обзор характеристик теплопередачи наножидкостей. Обновить. Поддерживать. Energy Rev.2007; 11: 512–523. DOI: 10.1016 / j.rser.2005.01.010. [CrossRef] [Google Scholar] 6. Ломасколо М., Коланджело Г., Миланезе М., де Ризи А. Обзор теплопередачи в наножидкостях: экспериментальные результаты по проводимости, конвекции и излучению.Обновить. Поддерживать. Energy Rev.2015; 43: 1182–1198. DOI: 10.1016 / j.rser.2014.11.086. [CrossRef] [Google Scholar] 7. Сюань Ю., Ли К. Улучшение теплопередачи наножидкостей. Int. J. Тепловой поток жидкости. 2000. 21: 58–64. DOI: 10.1016 / S0142-727X (99) 00067-3. [CrossRef] [Google Scholar] 8. Гу Б., Хоу Б., Лу З., Ван З., Чен С. Теплопроводность наножидкостей, содержащих наполнители с высоким соотношением сторон. Int. J. Heat Mass Transf. 2013; 64: 108–114. DOI: 10.1016 / j.ijheatmasstransfer.2013.03.080. [CrossRef] [Google Scholar] 9.Минца Х.А., Рой Г., Нгуен К.Т., Дусет Д. Новые данные о температурно-зависимой теплопроводности для наножидкостей на водной основе. Int. J. Therm. Sci. 2009. 48: 363–371. DOI: 10.1016 / j.ijthermalsci.2008.03.009. [CrossRef] [Google Scholar] 10. Эллахи Р., Хассан М., Зишан А. Влияние формы наноразмерных частиц в наножидкости Cu – H 2 O на генерацию энтропии. Int. J. Heat Mass Transf. 2015; 81: 449–456. DOI: 10.1016 / j.ijheatmasstransfer.2014.10.041. [CrossRef] [Google Scholar] 11. Пак Б.С., Чо Ю.И. Исследование гидродинамики и теплообмена дисперсных жидкостей с субмикронными частицами оксидов металлов.Exp. Теплопередача. Int. J. 1998; 11: 151–170. DOI: 10.1080 / 089808946559. [CrossRef] [Google Scholar] 12. Фард М.Х., Исфахани М.Н., Талаи М. Численное исследование конвективного теплообмена наножидкостей в двухфазной модели с круглой трубкой по сравнению с однофазной моделью . Int. Commun. Тепло-массообмен. 2010; 37: 91–97. DOI: 10.1016 / j.icheatmasstransfer.2009.08.003. [CrossRef] [Google Scholar] 13. Рахман С.Ю., Эллахи Р., Надим С., Зия К.М.З. Одновременное воздействие наночастиц и проскальзывания жидкости Джеффри через сужающуюся артерию с легким стенозом.J. Mol. Liq. 2016; 218: 484–493. DOI: 10.1016 / j.molliq.2016.02.080. [CrossRef] [Google Scholar] 14. Коланджело Г., Фавале Э., Мильетта П., Миланез М., де Ризи А. Теплопроводность, вязкость и стабильность Al 2 O 3 -диатермические масляные наножидкости для систем солнечной энергетики. Энергия. 2016; 95: 124–136. DOI: 10.1016 / j.energy.2015.11.032. [CrossRef] [Google Scholar] 15. Коланджело Г., Фавале Э., де Ризи А., Лафорджа Д. Результаты экспериментальных исследований теплопроводности наножидкостей на основе диатермического масла для высокотемпературных применений.Прил. Энергия. 2012; 97: 828–833. DOI: 10.1016 / j.apenergy.2011.11.026. [CrossRef] [Google Scholar] 16. Ли Г.Дж., Ри К.К. Повышенная теплопроводность наножидкостей, содержащих нанопластинки графена, полученных с помощью ультразвукового облучения. J. Mater. Sci. 2014; 49: 1506–1511. DOI: 10.1007 / s10853-013-7831-6. [CrossRef] [Google Scholar] 17. Баландин А.А., Гош С., Бао В., Калисо И., Тевелдебрахан Д., Мяо Ф., Лау К.Н. Превосходная теплопроводность однослойного графена. Nano Lett. 2008; 8: 902–907. DOI: 10.1021 / nl0731872. [PubMed] [CrossRef] [Google Scholar] 18. Ахмад И., Маккарти Дж. Э., Баранов А., Гунько Ю. К. Разработка противоэлектродов на основе графеновых нанопластинок для солнечных элементов. Материалы. 2015; 8: 5953–5973. DOI: 10.3390 / ma8095284. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] 19. Ли Х., Чен Ю., Мо С., Цзя Л., Шао Х. Влияние модификации поверхности на стабильность и теплопроводность графеновой наножидкости на водной основе SiO 2 с покрытием. Термохим. Acta. 2014; 595: 6–10.DOI: 10.1016 / j.tca.2014.09.006. [CrossRef] [Google Scholar] 20. Амири А., Садри Р., Шанбеди М., Ахмади Г., Чу Б. Т., Кази С. Н., Дахари М. Зависимость характеристик термосифона от подходов функционализации: экспериментальное исследование теплофизических свойств водных наножидкостей на основе графеновых нанопластинок. Energy Convers. Manag. 2015; 92: 322–330. DOI: 10.1016 / j.enconman.2014.12.051. [CrossRef] [Google Scholar] 21. Иджам А., Моради Гольшейх А., Сайдур Р., Ганесан П. Наножидкость на основе глицерина и воды, содержащая нанолисты оксида графена.J. Mater. Sci. 2014; 49: 5934–5944. DOI: 10.1007 / s10853-014-8312-2. [CrossRef] [Google Scholar] 22. Ярманд Х., Гарехкхани С., Ахмади Г., Ширази С.Ф.С., Барадаран С., Монтазер Э., Зубир М.Н.М., Алехашем М.С., Кази С., Дахари М. Гибридные наножидкости графеновые нанопластинки и серебра для улучшения теплопередачи. Energy Convers. Manag. 2015; 100: 419–428. DOI: 10.1016 / j.enconman.2015.05.023. [CrossRef] [Google Scholar] 23. Вэнь Д., Линь Г., Вафаэй С., Чжан К. Обзор наножидкостей для приложений теплопередачи.Партикуология. 2009; 7: 141–150. DOI: 10.1016 / j.partic.2009.01.007. [CrossRef] [Google Scholar] 24. Рудяк В.Ю. Вязкость наножидкостей — почему она не описывается классическими теориями. Adv. Нанопарт. 2013; 2: 266–279. DOI: 10.4236 / anp.2013.23037. [CrossRef] [Google Scholar] 25. Гупта С.С., Шива М.В., Кришнан С., Срипрасад Т.С., Сингх П.К., Прадип Т., Дас С.К. Повышение теплопроводности наножидкостей, содержащих нанолисты графена. J. Appl. Phys. 2011; 110 дой: 10,1063 / 1,3650456. [CrossRef] [Google Scholar] 26.Хаджар З., Рашиди А.М., Гозатлоо А. Повышенная теплопроводность наножидкостей оксида графена. Int. Commun. Тепло-массообмен. 2014; 57: 128–131. DOI: 10.1016 / j.icheatmasstransfer.2014.07.018. [CrossRef] [Google Scholar] 27. Ю. В., Се Х., Чен В. Экспериментальное исследование теплопроводности наножидкостей, содержащих нанолисты оксида графена. J. Appl. Phys. 2010; 107 DOI: 10.1063 / 1.3372733. [CrossRef] [Google Scholar] 28. Садегинежад Э., Тогун Х., Мехрали М., Неджад П.С., Латибари С.Т., Абдулраззак Т., Kazi S., Metselaar H.S.C. Экспериментальное и численное исследование увеличения теплопередачи для наножидкостей из графеновых нанопластинок в условиях турбулентного потока. Int. J. Heat Mass Transf. 2015; 81: 41–51. DOI: 10.1016 / j.ijheatmasstransfer.2014.10.006. [CrossRef] [Google Scholar] 29. Ярманд Х., Гареххани С., Ширази С.Ф.С., Амири А., Алехашем М.С., Дахари М., Кази С. Экспериментальное исследование теплофизических свойств, конвективной теплопередачи и падения давления водной наножидкости функционализированных графеновых нанопластинок в квадратной нагретой трубе .Energy Convers. Manag. 2016; 114: 38–49. DOI: 10.1016 / j.enconman.2016.02.008. [CrossRef] [Google Scholar] 30. Соланги К., Амири А., Лухур М., Гавими С.А.А., Зубир М.Н.М., Кази С., Бадарудин А. Экспериментальное исследование графеновых нанопластинок, обработанных пропиленгликолем, для улучшения турбулентной конвективной теплопередачи с закрытым каналом. Int. Commun. Тепло-массообмен. 2016; 73: 43–53. DOI: 10.1016 / j.icheatmasstransfer.2016.02.003. [CrossRef] [Google Scholar] 31. Ting H.H., Hou S.S. Исследование ламинарной конвективной теплопередачи для наножидкостей Al 2 O 3 — воды, протекающих через канал квадратного поперечного сечения с постоянным тепловым потоком.Материалы. 2015; 8: 5321–5335. DOI: 10.3390 / ma8085246. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] 32. Шейхолеслами М., Эллахи Р. Электрогидродинамическая гидротермальная обработка наножидкостями в камере с синусоидальной верхней стенкой. Прил. Sci. 2015; 5: 294–306. DOI: 10.3390 / app5030294. [CrossRef] [Google Scholar] 33. Рашиди С., Дехган М., Эллахи Р., Риаз М., Джамал-Абад М.Т. Исследование потокового поперечного течения магнитной жидкости с теплопередачей вокруг препятствия, внедренного в пористую среду. Дж.Magn. Magn. Матер. 2015; 378: 128–137. DOI: 10.1016 / j.jmmm.2014.11.020. [CrossRef] [Google Scholar] 34. Шейхолеслами М., Эллахи Р. Трехмерное мезоскопическое моделирование влияния магнитного поля на естественную конвекцию наножидкости. Int. J. Heat Mass Transf. 2015; 89: 799–808. DOI: 10.1016 / j.ijheatmasstransfer.2015.05.110. [CrossRef] [Google Scholar] 35. Шер Акбар Н., Раза М., Эллахи Р. Влияние наведенного магнитного поля и теплового потока с суспензией углеродных нанотрубок на перистальтический поток в проницаемом канале.J. Magn. Magn. Матер. 2015; 381: 405–415. DOI: 10.1016 / j.jmmm.2014.12.087. [CrossRef] [Google Scholar] 36. Кальво-Браво Дж., Кабалейро Д., Пиньейро М.М., Луго Л. Магнитореологическое поведение наножидкостей гематита на основе пропиленгликоля. Реол. Acta. 2015; 54: 757–769. DOI: 10.1007 / s00397-015-0868-5. [CrossRef] [Google Scholar] 37. Lemmon E.W., Huber M.L., McLinden M.O. Эталонные термодинамические и транспортные свойства жидкости (REFPROP) Национальный институт стандартов и технологий; Гейтерсбург, Мэриленд, США: 2010.Стандартная справочная база данных NIST. [Google Scholar] 38. Кабалейро Д., Грасиа-Фернандес К., Легидо Дж. Л., Луго Л. Удельная теплоемкость наножидкостей оксидов металлов при высоких концентрациях для теплопередачи. Int. J. Heat Mass Transf. 2015; 88: 872–879. DOI: 10.1016 / j.ijheatmasstransfer.2015.04.107. [CrossRef] [Google Scholar] 39. Кабалейро Д., Нимо Дж., Пасториса-Гальего М.Дж., Пиньейро М.М., Легидо Дж. Л., Луго Л. Теплопроводность сухих нанопорошков анатаза и рутила и наножидкостей TiO 2 на основе этилена и пропиленгликоля.J. Chem. Термодин. 2015; 83: 67–76. DOI: 10.1016 / j.jct.2014.12.001. [CrossRef] [Google Scholar] 40. Кабалейро Д., Пасториса-Галлего М.Дж., Пинейро М.М., Легидо Дж. Л., Луго Л. Теплофизические свойства смесей (дифениловый эфир + бифенил) для их использования в качестве теплоносителей. J. Chem. Термодин. 2012; 50: 80–88. DOI: 10.1016 / j.jct.2012.02.001. [CrossRef] [Google Scholar] 41. Кабалейро Д., Пасториса-Галлего М.Дж., Пинейро М.М., Луго Л. Характеристика и измерения теплопроводности, плотности и реологических свойств наночастиц оксида цинка, диспергированных в смеси (этан-1,2-диол + вода).J. Chem. Термодин. 2013; 58: 405–415. DOI: 10.1016 / j.jct.2012.10.014. [CrossRef] [Google Scholar] 42. Гниелинский В. Теплообмен в концентрических кольцевых и параллельных пластинчатых каналах. VDI Heat Atlas. Springer; Гейдельберг, Германия: 2010. С. 701–708. [Google Scholar] 43. Ким К.С. Теплофизические свойства нержавеющих сталей. Аргоннская национальная лаборатория; Аргонн, Иллинойс, США: 1975. Технический отчет. [Google Scholar] 44. Бьянко В., Манка О., Нардини С., Вафай К. Улучшение теплопередачи с помощью наножидкостей. CRC Press; Бока-Ратон, Флорида, США: 2015.[Google Scholar] 45. Mehrali M., Sadeghinezhad E., Rosen M.A., Akhiani A.R., Tahan Latibari S., Mehrali M., Metselaar H.S.C. Теплопередача и генерация энтропии для ламинарного потока вынужденной конвекции графеновых нанопластинок наножидкости в горизонтальной трубе. Int. Commun. Тепло-массообмен. 2015; 66: 23–31. DOI: 10.1016 / j.icheatmasstransfer.2015.05.007. [CrossRef] [Google Scholar] 46. Объединенный комитет руководств по метрологии. Оценка данных измерений — Руководство по выражению неопределенности в измерениях.JCGM 100; Севр, Франция: 2008 г. [Google Scholar]Frontiers | Численное моделирование корреляции коэффициента теплопередачи для распылительного охлаждения при непрерывной разливке
Введение
Сегодня в мире более 90% стальных полуфабрикатов производится методом непрерывной разливки (Dantzig and Rappaz, 2016). В процессе разливки очищенная жидкая сталь, прошедшая обработку в ковше, перемещается из печи-ковша в промежуточный ковш, который служит резервуаром и поддерживает уровень жидкой стали во время замены ковша.Сталь разливают вертикально после стекания из нижней части разливочного ковша в верхнюю часть разливочной машины. Когда жидкая сталь попадает в прямоугольную форму, она затвердевает в виде тонкой твердой оболочки на стенках охлаждаемой водой формы. Этот процесс начального затвердевания называется процессом первичного охлаждения. Ряд валков, расположенных под кристаллизатором, непрерывно отводит вновь образованную тонкую оболочку вместе с заключенной в нее расплавленной сталью во вторичную зону охлаждения, где полутвердую сталь дополнительно охлаждают с помощью нескольких рядов струй воды.Как только сталь станет твердой, ее можно разрезать на сегменты различной длины с помощью кислородной горелки для последующей обработки.
В зоне вторичного охлаждения скорость распылительного охлаждения должна быть тщательно спроектирована и контролироваться для получения высококачественной и высокопрочной стали. В противном случае неравномерно распределенное температурное поле внутри затвердевшей оболочки вызовет остаточные термические напряжения и деформации, которые в конечном итоге приведут к растрескиванию и другим дефектам (Laitinen and Neittaanmäki, 1988; Sengupta et al., 2005). Однако невозможно измерить распределение температуры внутри затвердевшей стали во время непрерывной разливки. В качестве альтернативы было предложено использовать HTC на стальной поверхности для количественной оценки степени и равномерности распылительного охлаждения. С точки зрения теплопередачи, HTC можно вывести из закона охлаждения Ньютона:
qtotal ″ = qcond ″ + qconv ″ + qR ″ = HTC (Tface-Tspray) + qR ″ (1)Как показано в уравнении. 1 HTC представляет собой комбинированный эффект теплопроводности между каплей воды и горячей сталью и конвекции за счет вовлечения воздуха.Уравнение 1 также подчеркивает сущность систем управления разливкой, используемых на современных сталелитейных заводах. На рисунке 1 показана типовая схема управления непрерывной разливкой. Основная цель системы управления состоит в том, чтобы постоянно прогнозировать степень затвердевания или толщину твердой оболочки в любой точке зоны вторичного охлаждения, чтобы машины для литья под давлением могли гибко работать, сохраняя при этом важные параметры в требуемых диапазонах (Thomas and Ho , 1996). Прогноз достигается путем решения уравнения сохранения энергии в полузатвердевшей стальной плите с условиями охлаждения поверхности, определенными в формуле.1 в качестве граничного условия. Прогнозируемая толщина твердого тела, а также металлургическая длина (полное затвердевание) должны поддерживаться в расчетном диапазоне. Как только прогноз отклоняется от желаемого значения, система немедленно реагирует и динамически регулирует либо скорость разливки, либо расход распыляемой воды.
РИСУНОК 1 . Типовая схема управления непрерывной разливкой.
В то же время остается проблемой получить точные значения HTC в различных условиях эксплуатации.Хорошо известно, что HTC является локализованным параметром, и его значение варьируется во всей области вторичного охлаждения (Sengupta et al., 2005). Компания HTC чувствительна как к конфигурации форсунок, так и к условиям эксплуатации литья. Некоторые из наиболее известных параметров, влияющих на HTC, включают тип сопла, расход распыляемой воды, угол распыления, расстояние зазора, температуру стальной поверхности, направление распыления и расстояние от сопла до сопла. На практике исследователи коррелировали HTC с наиболее важными рабочими параметрами, такими как скорость литья и расход распыляемой воды, с помощью небольшого эксперимента с горячей пластиной (Nozaki et al., 1978; Моралес и др., 1990; Horsky et al., 2005; Blazek et al., 2013; Long et al., 2018). Наиболее известная корреляция была разработана Нозаки (Nozaki et al., 1978) и показана в уравнении. 2. Это уравнение учитывает как поток распыляемой воды, так и температуру распыляемой воды, так как оба параметра важны для процесса распылительного охлаждения и их относительно удобно получить с помощью измерений на месте. Нодзаки также признает различия между машинами для литья под давлением, добавляя зависящий от машины параметр калибровки αcal.Зная конкретное расположение форсунок, этот коэффициент можно легко настроить. Благодаря своей простоте и гибкости, эта корреляция широко используется с 1970-х годов. Некоторые из последних корреляций HTC являются либо вариациями корреляции Нозаки (Brimacombe et al., 1980; Hardin et al., 2000; Hardin et al., 2003; Meng and Thomas, 2003; Mosayebidorcheh and Gorji-Bandpy, 2017; Hardin and Beckermann, 2018) или расширение этой формулы (Blazek et al., 2013).
HTC = 22500Qwater0.55 (1−0,0075Tspray) / αcal (2)С другой стороны, другие важные параметры литья, такие как температура поверхности стали, скорость разливки и расстояние от сопла до сопла, не включены в формулу. 2. Например, было доказано, что температура поверхности стали влияет на теплопередачу при ударе капель и локальную температуру Лейденфроста (Bernardin and Mudawar, 1999). Скорость литья может изменять время пребывания капель на стальной поверхности, тем самым увеличивая или уменьшая количество передаваемой энергии. При этом теплоотдача заметно увеличивается под зоной перекрытия распылителей на небольшом расстоянии от сопла до сопла.Таким образом, необходимо разработать более полные и общие корреляции HTC для включения этих явлений. Кроме того, стоит упомянуть, что существующие соотношения были специально разработаны для ограниченного числа форсунок и условий эксплуатации. Каждое условие литья требует по крайней мере одного эксперимента для однозначного определения коэффициентов корреляции, и корреляция может быть неприменимой, когда происходят изменения в процессе литья.
С развитием техники высокопроизводительных параллельных вычислений (HPC) численные модели на основе вычислительной гидродинамики (CFD) стали мощным инструментом для понимания сложных проблем потока жидкости и теплопередачи.Основным преимуществом подхода CFD на основе высокопроизводительных вычислений является создание крупномасштабных симуляций в разумно короткие сроки. Гораздо эффективнее построить корреляции HTC на основе численного моделирования. Тем не менее, корреляции HTC на основе CFD для непрерывной разливки все еще недоступны, в основном из-за сложных аэродинамических характеристик при распылении и последующем переносе тепла при ударе между каплями воды и горячей сталью. Точная CFD-модель процесса распылительного охлаждения играет ключевую роль в разработке надежных корреляций HTC.
Таким образом, в настоящем исследовании предлагается новая эффективная методология численного расчета корреляций HTC для непрерывной разливки стали. Методология включает высокоточные трехмерные модели CFD распылительного охлаждения с учетом распыления и теплопередачи со столкновением, а также регрессионного анализа. Моделирование CFD предсказывает подробный эффект охлаждения распылением на стальную поверхность в различных рабочих условиях, тогда как регрессионный анализ преобразует результаты моделирования в математически простую корреляцию, которую можно использовать в качестве граничного условия для отверждения на месте в автономном / оперативном режиме. расчет.Кроме того, был разработан графический интерфейс пользователя (GUI) для облегчения использования корреляции. Методология, представленная в текущем исследовании, должна принести пользу сталелитейной промышленности за счет ускорения процесса разработки корреляций HTC, достижения управления динамическим охлаждением распылением в реальном времени, поддержки выбора сопел, устранения неисправностей в работе сопел и может еще больше повысить точность существующих систем управления литьем. .
Методология
Численный подход
На рисунке 2 показан процесс разработки корреляций HTC с использованием численного подхода.Подход состоит из этапа численного моделирования, этапа анализа данных и этапа разработки графического интерфейса пользователя. Разработка CFD-модели — это первый шаг на этапе численного моделирования. Модель содержит наиболее важные физические аспекты процесса распылительного охлаждения, такие как распыление, дробление капель, столкновение капель, увлечение воздуха, теплопередача при ударе капли о сталь и охлаждение стальных слябов. Второй шаг — создание базы данных HTC с помощью параметрического исследования. На этом этапе моделируются различные конфигурации форсунок и рабочие условия литья.На этапе анализа данных распределения различных профилей HTC на стальной поверхности разлагаются на две нормализованные универсальные функции распределения, тогда как величина HTC сводится к характеристическому значению, которое коррелируется с восемью репрезентативными рабочими параметрами посредством регрессионного анализа или подбора кривой. . Наконец, удобный графический интерфейс, основанный на платформе Unity® 3D, вычисляет локальные значения HTC на основе предварительно определенной корреляции и вводимых пользователем данных.
РИСУНОК 2 .Процесс разработки корреляции HTC на основе CFD.
Численные модели
При численном моделировании основное внимание уделяется распылению и переносу тепла при ударе каплями стали. Распад струи воды не включен в текущую модель, но капли, образующиеся в результате распада струи, отслеживаются в лагранжевой системе отсчета от длины разрыва до конца их срока службы. Движение капель решается путем интегрирования второго закона Ньютона. Воздухововлечение из-за высокоскоростной закачки воды и горячего стального сляба моделируется как непрерывные фазы в системе Эйлера.
Непрерывная фаза
Стационарные усредненные по Рейнольдсу уравнения Навье-Стокса для массы, импульса, энергии и переноса частиц (капля воды в водяной пар) решаются для воздуха, тогда как для стальной плиты требуется только уравнение энергии. для теплопроводности, конвекции и излучения. Эти уравнения сохранения можно выразить в следующем общем виде (Mundo et al., 1997; Liu et al., 2018):
∇⋅ (ρairu → airφ − Γφ∇φ) = Sφ + Sdrop-air (3), где φ — универсальная переменная, которая представляет собой уравнение массы, скорость в уравнении количества движения, энтальпию в уравнении энергии и массовую долю в уравнении переноса частиц.Sφ — член внутреннего источника, соответствующий универсальной переменной. Капля-воздух — это внешний источник, который учитывает взаимодействие капля-воздух. Сначала решаются основные уравнения для воздуха, а затем отслеживается нестационарное отслеживание капель. Скорость воздуха в каждой вычислительной ячейке используется для получения движения капли при интегрировании закона движения Ньютона. В конце каждого временного шага капли, изменения массы, импульса и энергии в каплях включаются в последующие вычисления для воздуха посредством внешнего источника.
Модель турбулентности k — ω Перенос сдвигового напряжения (SST) учитывает кинетическую энергию турбулентности и удельную скорость диссипации турбулентности. Эта модель выбрана из-за ее высокой точности в прогнозировании наличия вихрей вдоль границы струи и отрыва потока на стальной поверхности без использования слишком больших вычислительных мощностей. Модель использует преимущества модели k — ε в объемной области и модели k — ω вблизи стенок с функцией смешивания для перехода между двумя моделями (Menter, 1993; Zukerman и Лиор, 2006).
Дискретная фаза
Образование капель
Физически капли образуются в результате двух последовательных процессов разрушения, то есть разрушения жидкого слоя и разрыва связок. Два процесса дробления вместе называются первичным дроблением, в отличие от вторичного дробления, когда капли, образовавшиеся в процессе первичного дробления, далее распадаются на более мелкие капли из-за аэродинамической нестабильности или столкновений капель с каплями. Первичный распад — хорошо изученный процесс, и соответствующие теории были строго подтверждены за последние несколько десятилетий (Rayleigh, 1878; Weber, 1931; Ohnesorge, 1936; Reitz, 1978a; Reitz, 1987b; Nijdam et al., 2006; Fung et al., 2012). В текущем исследовании используется модель LISA для прогнозирования образования капель на длине разрушения без моделирования внутреннего потока внутри сопла и процесса первичного разрушения.
На рисунке 3 показан процесс образования и закачки капель, применяемый в данном исследовании. Модель LISA (O’Rourke, 1981; Senecal et al., 1999) предполагает, что струя жидкости, выходящая из сопла, представляет собой двумерный слой вязкой несжимаемой жидкости, который распадается на связки, а затем на капли из-за роста бесконечно малых волновых возмущений после перемещения. на определенном расстоянии (длине разрыва) от среза сопла.Длина развала определяется наиболее нестабильным возмущением и скоростью его роста:
РИСУНОК 3 . Метод генерации капель по модели LISA.
В начале каждого временного шага капли, ti, группа капель вводится в расчетную область из виртуальной криволинейной плоскости впрыска, расположенной на расстоянии длины разрыва ниже среза сопла. Общая масса введенных капель равна массе воды, протекающей через сопло, которую можно определить из условий эксплуатации отливки.Капли случайным образом распределяются в плоскости впрыска, но их распределение по размерам удовлетворяет распределению Розина-Раммлера с числом разброса 3,5. Характерный диаметр распределения Розина-Раммлера можно вычислить из следующего выражения:
d0 = 3,76πCLKs (1 + 3Oh) 1/6 (5)Движение капли
Движение капли в пределах каждого временного шага отслеживается в лагранжиане. кадра путем решения закона движения Ньютона:
du → dropdt = 3μdropCDRedrop4ρdropddrop2 (u → air − u → drop) + g → (ρdrop − ρair) ρdrop (6)Движение капли определяется силой сопротивления и гравитационной силой одновременно с предположением эта капля остается сферической на протяжении всей своей жизни.Член силы сопротивления представляет собой взаимодействие воздушной капли, а коэффициент сопротивления CD может быть найден из следующей кусочной функции (Liu et al., 1993):
CD = {0,42424Redrop (1 + 16Redrop2 / 3) Redrop> 1000Redrop ≤1000 (7)Модель времени жизни вихря также включена для моделирования рассеивания капель во время распыления из-за турбулентности в газовой фазе (Gosman and Ioannides, 1983).
Изменение температуры и массы капли
Капля также обменивается теплом с окружающим воздухом во время движения через газовую фазу.Изменение температуры капли определяется сохранением энергии:
mdropcpdTdropdt = πddrop2h (T∞ − Tdrop) + dmdropdthfg + πddrop2εdropσSB (TR4 − Tdrop4) (8)Коэффициент конвективной теплопередачи h можно получить из Модель Ранца-Маршалла (Ranz and Marshall, 1952):
Nudrop = hddropkair = 2,0 + 0,6 Redrop0,5Pr0,33 (9)Тем временем капля жидкости испаряется в водяной пар, который затем диффундирует в окружающую газовую фазу до тех пор, пока существует разница концентраций между поверхностью капли и жидкостью в объеме.Этот процесс моделируется путем постоянного обновления массы капли на каждом временном шаге капли:
dmdropdt = πddrop2kc (Cs − C∞) (10)Коэффициент массопереноса, kc, можно получить из следующей корреляции чисел Шервуда:
Shdrop = kcddropDvapor = 2.0 + 0.6Redrop0.5Sc0.33 (11)Распад и столкновение капель
Прогнозирование распада капель и столкновений имеет решающее значение для последующего переноса тепла при ударе капли о сталь. Количество и размер капель претерпевают значительные изменения во время этих двух событий.Модель развала WAVE применяется в текущем исследовании для учета разрушения капель, вызванного относительной скоростью между каплей и окружающим воздухом. Модель является аналогом теории неустойчивости струи. Модель предполагает, что время разрушения капли и результирующий размер дочерней капли зависят от наиболее быстрорастущей нестабильности Кельвина-Гельмгольца:
drparentdt = −ΛΩ (rparent − rchild) 3,726B1rparent (13)Столкновение капли с каплей рассчитывается по Алгоритм О’Рурка (О’Рурк, 1981).Алгоритм дает стохастическую оценку столкновений вместо того, чтобы вычислять, пересекаются ли траектории двух капель. На каждом временном шаге капли считается, что они могут столкнуться, только если они присутствуют в одной и той же вычислительной ячейке, а меньшая капля находится в объеме столкновения с центром в большей. Объем столкновения определяется как цилиндр длиной (u1 − u2) Δt и площадью круга π (r1 + r2) 2. Если условие выполнено, две капли могут столкнуться.Согласно концепции коллизионного объема, вероятность коллизии может быть определена следующим образом:
n¯ = n2π (r1 + r2) 2 (u1 − u2) ΔtVcell (15)Результат столкновения зависит от смещения траектория от меньшей капли к большей. Смещение является функцией межцентрового расстояния между двумя каплями и случайным числом, которое напоминает случайность столкновений:
Вычисленное смещение сравнивается с критическим значением, определенным следующим образом:
bcrit = (r1 + r2) min ( 1.0,2.4fWe) (17) f = (r1r2) 3−2.4 (r1r2) 2 + 2.7 (r1r2) (18) Если boffset На рис. 4 показан расчет ударов стальных капель и теплопередачи. На рисунке изображены жидкая ячейка, твердая ячейка, а также капля воды.Когда капля входит в ячейку с жидкостью, прилегающую к твердой ячейке, и ударяется о границу раздела жидкость-твердое тело, результат столкновения зависит от свойств поступающей капли и рассчитывается с помощью модели пристенной струи (Naber and Reitz, 1988). В модель столкновения включены три исхода: отложение, отражение и пристенная струя. В режиме осаждения капля остается на поверхности стали после удара и продолжает отводить тепло от стали до полного испарения. В режиме отражения вертикальная составляющая скорости капли до столкновения изменяется на противоположный знак после столкновения, сохраняя при этом величину.И направление, и величина касательной составляющей скорости остаются неизменными. РИСУНОК 4 . Расчет теплопередачи при ударе капли стали (A) до удара и (B) после удара. Режим пристенной струи, однако, активируется, когда группа близко расположенных капель падает на стальную поверхность. Этот непрерывный поток капель теряет вертикальную составляющую скорости и после столкновения поворачивается в горизонтальное направление, что можно рассматривать как невязкую струю, исходящую из точки застоя на поверхности.Как показано на рисунке 5, высота пристенной струи H является функцией угла, под которым капля выходит из горизонтального падения: Где Hπ — высота при Ψ = π. Константа β определяется из сохранения массы и количества движения и дается Набером и Рейцем (Naber and Reitz, 1988): РИСУНОК 5 . Иллюстрация режима соударения со стенкой. Теплообмен между каплями стали проиллюстрирован на Рисунке 4B.Хотя предполагается, что капля имеет сферическую форму на протяжении всего срока службы, эффект деформации капли учитывается при расчете теплопередачи. Настоящее исследование предполагает, что капля при ударе деформируется в цилиндр равного объема и остается в контакте с горячей поверхностью в течение короткого периода времени. Деформированная капля и сталь обмениваются теплом за счет чистой теплопроводности: Эффективная площадь контакта, Acond, и время контакта определяются следующим образом (Akao et al., 1980; Birkhold, 2007): Еще одним важным явлением во время распылительного охлаждения является эффект Лейденфроста. Это происходит, когда температура поверхности стали выше температуры Лейденфроста. В этой ситуации капля жидкости испаряется в пар сразу после удара. Из-за низкой теплопроводности пар, парящий над поверхностью, действует как изоляционный слой, предотвращая дальнейший контакт между каплей жидкости и горячей поверхностью.Следует отметить, что температура поверхности стали обычно выше, чем температура Лейденфроста в процессе непрерывной разливки (Бернардин и Мудавар, 1999). Таким образом, коэффициент, то есть эффективность теплопередачи, включен в модель ударной теплопередачи для учета снижения теплового потока через стальную поверхность из-за наличия парового слоя. Коэффициент — это отношение фактического теплового потока к максимальному тепловому потоку, который может быть достигнут. Для расчета коэффициента применяется экспериментальная эмпирическая корреляция (Issa, 2004): HTC оценивается в постобработке после завершения моделирования. На практике удобно объединить теплопроводность и конвекцию в один термин и представить эту величину теплопередачи по закону охлаждения Ньютона. На основании уравнения. 1 и 4, с учетом сохранения энергии, полный тепловой поток, который передается от центроида твердой ячейки к центроиду границы раздела жидкость-твердое тело, можно записать следующим образом: Где Tcell — температура твердого центроида, Tface — температура центроида поверхности раздела, Δy — расстояние от центроида твердого тела до центроида грани и равно на половине высоты ячейки Tdrop — это температура капли при ударе.Однако в реальности невозможно измерить температуру каждой индивидуальной капли до и после столкновения. Более практичный метод, принятый сталелитейной промышленностью, заключается в замене термина на температуру распыляемой воды, которую можно измерить и контролировать. В текущем исследовании также используется это определение для получения согласованных значений HTC. Переставляя уравнение. 25 и решив для HTC, получим следующее выражение: В процессе непрерывной разливки область вторичного охлаждения расширяется от выхода формы до точки отсечки, а общая длина этой области составляет от 10 до 40 м.Кроме того, на обеих широких сторонах стальной полосы размещены сотни чередующихся водяных струй и вальцов. С другой стороны, средний размер капли жидкости составляет всего около 300 мкм, и вычислительные ячейки в моделировании CFD должны иметь сопоставимый размер, чтобы детально разрешить взаимодействие капля-воздух, взаимодействие капля-капля и взаимодействие капля-сталь. Следовательно, более эффективный способ моделирования процесса охлаждения распылением — это моделирование небольшой части всей разливочной машины.На рисунке 6 показана вычислительная область, применяемая в данном исследовании. Домен состоит только из одного распылителя и цельного стального сегмента толщиной 30 мм. На практике тип форсунки, угол распыления, расход воды, расстояние от распыления и расстояние от распылителя до распылителя различаются от распылителя к распылителю, но текущая расчетная область может использоваться для моделирования различных распылений с небольшими изменениями граничных условий. . РИСУНОК 6 . Расчетная область и граничные условия для моделирования распылительного охлаждения. Впрыск капель, разрушение, столкновение, столкновение и испарение решаются в области жидкости, тогда как теплопроводность внутри стальной плиты рассчитывается в твердой области. Средняя толщина затвердевшей оболочки составляет от 25 до 30 мм на выходе из формы, а скорость роста оболочки оценивается от 0,1 мм / с до 0,4 мм / с (Tang et al., 2012). Таким образом, сляб толщиной 30 мм, применяемый в текущем исследовании, достаточно толстый, чтобы учесть температурный градиент внутри сплошного стального сляба, но достаточно тонкий, чтобы исключить затвердевание внутри стального сляба.При нормальной скорости разливки 1 м / мин стальному слябу требуется 6 с, чтобы пройти струю, охватывающую 100 мм в направлении разливки, но для того, чтобы капли, движущиеся со скоростью 13 м / с, достигли стали, требуется всего 0,01 с. поверхность, которая находится на 130 мм ниже кончика сопла. Из-за резкой разницы во времени численно удобно и эффективно исключить процесс затвердевания из текущего моделирования. Все поверхности области текучей среды настроены как выходы давления, за исключением интерфейса, как показано на рисунке 6.Тепловые условия на границе раздела определяются сопряженной теплопередачей. Две боковые поверхности твердой области, параллельные направлению разливки, рассматриваются как симметричные плоскости с предположением, что теплопроводность через эти поверхности незначительна. Предполагается, что распределение температуры на поверхности выше по потоку удовлетворяет линейному распределению из-за того, что смоделированная твердая область составляет лишь небольшую часть всего стального сляба (Корич и Томас, 2006). Нижний и верхний пределы распределения температуры получены из исторических данных на плоскости.Фиксированная температура назначается нижней поверхности, а ее величина устанавливается равной максимальной температуре на поверхности выше по потоку, чтобы гарантировать соответствие граничных условий. Начальная температура центроида грани на нижней по потоку поверхности твердой области устанавливается равной температуре ближайшего центроида ячейки. Температура центроида лица постоянно обновляется во время моделирования в соответствии с условиями на входе. Кроме того, к сплошной области применяется движущаяся система отсчета, чтобы представить движение стальной плиты в реальном процессе. Гексаэдральная сетка с неравномерными интервалами применяется как в жидких, так и в твердых областях. Ячейки сетки смещены к центру струи и границе раздела жидкость-твердое тело, чтобы безразмерное расстояние до стенки y + было меньше единицы в непосредственной близости от границы раздела. Все симуляции проводились на платформе ANSYS Fluent 17.1. Переходное отслеживание капли выполняется после двухсот итераций для непрерывных фаз. Сходимость считается выполненной, когда все масштабированные остатки достигают 10 –6 . Восемь рабочих параметров определены как факторы, способствующие определению значений HTC, и они включают расход распыляемой воды, расстояние от сопла до сопла, расстояние зазора, температуру распыляемой воды, скорость разливки, расстояние между соседними рядами распылителей, распыление. угол и направление распыления. В таблице 1 приведены все факторы и их соответствующие диапазоны, использованные в текущем исследовании. Примечательно, что единица измерения каждого фактора конвертируется в соответствии с режимом работы завода.Кроме того, температура поверхности сляба исключена из параметрического исследования по двум причинам: 1) температура поверхности сляба выше температуры Лейденфроста (700–1000 ° C) при непрерывной разливке стали. В таких условиях в отводе тепла во время распылительного охлаждения преобладает механизм паропленочного кипения. Изменение HTC в зависимости от температуры поверхности плиты незначительно (Sengupta et al., 2005). 2) температура поверхности сляба является одним из параметров, которые необходимо определить при расчете затвердевания, который зависит от HTC как теплового граничного условия. ТАБЛИЦА 1 . Краткое изложение факторов, влияющих на текущее исследование. Прогнозирование размера капли до столкновения имеет решающее значение для определения результатов столкновения и соответствующей скорости теплопередачи. Распределение размеров капель плоской веерной форсунки Lechler 660.766 (эквивалентный диаметр отверстия 1,9 мм и угол распыления 90 °) было экспериментально измерено одним из промышленных сотрудников. Сопло располагалось на расстоянии 130 мм от плоскости измерения.Жидкую воду вводили со скоростью три галлона в минуту (11,36 л в минуту) в изотермических условиях. Система лазерной визуализации VisiSize была адаптирована для измерения размера капель. Измеренный средний диаметр от 0 мм (центр распыления) до 120 мм (край распыления) с шагом 20 мм был сравнен с моделированием, и результат показан на рисунке 7. Прогнозируемый размер капель показывает хорошее совпадение с измеренным. данные. Размер капель намного меньше в ядре спрея, где концентрация капель самая высокая, в основном из-за интенсивного разрушения и столкновений.Хорошее соответствие размера капель в этой области предполагает, что текущая модель способна точно уловить наиболее важные явления внутри спрея. Прогнозы на краю аэрозоля, где преобладает взаимодействие капель с воздухом, немного ошибочны. Одна из возможных причин заключается в том, что сильное взаимодействие между двумя фазами приводит к другим типам распада, которые не включены в текущую модель. Тем не менее, большинство распылителей при непрерывной разливке предназначены для перекрытия с соседними распылителями, и эффект взаимодействия капель с воздухом значительно снижается в области перекрытия. РИСУНОК 7 . Сравнение размера капель в разных частях спрея. Модель ударной теплопередачи была проверена на эксперименте с горячей пластиной, проведенном в Технологическом университете Брно (Horsky et al., 2005). Перед экспериментом сегмент аустенитной пластины был нагрет до 1250 ° C. Все поверхности горячей плиты были покрыты изоляционными материалами, за исключением поверхности, обращенной к распылительному соплу.Пластина закреплялась над соплом, чтобы исключить образование водяной пленки на поверхности. Сопло было помещено на движущуюся тележку, которая может перемещаться вперед и назад во время эксперимента, чтобы имитировать относительное движение между стальной пластиной и распылителями при непрерывной разливке. Эксперимент прекращался, когда температура пластины была ниже 500 ° C. Набор термопар, встроенных в пластину, регистрировал внутренние температуры, а поверхностные HTC рассчитывались методом обратной теплоотдачи. На рисунке 8 показано сравнение интегрированных поверхностных HTC в различных местах на поверхности вместе с общим HTC.Прогнозируемые значения HTC согласуются с большинством измерений. Большие значения HTC в точках A и B указывают на интенсивное охлаждение распылением. Это связано с тем, что большое количество мелких капель с большим отношением поверхности к объему значительно способствует теплопередаче в центре распыляемой струи. Некоторые выбросы означают, что текущая модель недооценивает теплопередачу в некоторых местах на поверхности. Одна из возможных причин связана с процедурой эксперимента. Метод переходной горячей пластины предназначен для работы в широком диапазоне температур в одном эксперименте.В результате температура пластины может упасть ниже температуры Лейденфроста в конце эксперимента. При низких температурах поверхности капли жидкости могут напрямую контактировать с пластиной, что приводит к гораздо более высокому HTC. Без учета струйного охлаждения при температуре Лейденфроста текущая модель способна предсказать точные значения HTC. РИСУНОК 8 . Сравнение HTC на стальной поверхности. На рисунке 9 показано распределение температуры и HTC на стальной поверхности, охлаждаемой одним соплом с плоским вентилятором, при типичных условиях литья: Qwater = 7 л / мин, D-сопло = Drow = 650 мм, Hspray = 130 мм, Tspray = 300 K, Vcasting = 1 м / мин, θspray = 90 °, η = 1.Область низкотемпературного охлаждения распылением в середине узкая в направлении литья, но тянется почти на 200 мм в поперечном направлении, образуя видимый эллиптический узор на поверхности. Тот факт, что картина ударного теплообмена совпадает с формой струи с плоским веером, показывает доминирующее влияние характеристик струи на охлаждение струи. За пределами области охлаждения распылением стальная плита теряет тепло в окружающую среду за счет конвекции и излучения. Почти симметричный эллиптический узор также указывает на распределение капель на поверхности.После столкновения большинство капель разделяются на два потока и продолжают движение в поперечном направлении. Два потока отходят друг от друга в точке торможения, относительно которой эллиптическая структура симметрична. РИСУНОК 9 . (A) вид сверху температуры поверхности плиты и (B) вид сверху шаблона HTC. На рисунке 9B показан профиль HTC на поверхности. Локальные значения HTC вычисляются на основе уравнения. 26. Внутри профиля в форме бабочки HTC достигает пика около точки застоя, где импульс капли максимален.Согласно формуле. 24, эффективность теплопередачи увеличивается с увеличением числа Вебера для капель. В результате капли с большим импульсом дают более высокие значения HTC при ударе. Такое поведение подразумевает, что капли с высоким импульсом с большей вероятностью проникают в тонкий паровой слой, парящий над стальной поверхностью, и вступают в прямой контакт с поверхностью. В других условиях эксплуатации образуются аналогичные HTC-профили на стальной поверхности, но с некоторыми различиями в величине. Поскольку все профили HTC, предсказанные с помощью CFD, имеют одинаковое распределение в пространстве, гораздо удобнее создавать нормализованные универсальные функции распределения для всех рабочих условий.Распределение HTC на стальной поверхности можно разложить на две универсальные функции распределения. Один находится в направлении разливки (направление x ), а другой — в поперечном направлении (направление x ). Координаты вместе с соответствующим значением HTC в любой заданной точке профиля HTC, прогнозируемого CFD, нормализуются до значений от 0 до единицы на основе следующих определений: На рисунке 10 показаны форма и расположение двух нормализованных распределений HTC.Эти два распределения можно рассматривать как проекции двумерного паттерна HTC. Схема двух нормализованных универсальных функций распределения может быть получена путем аппроксимации кривой и выражается следующим образом: РИСУНОК 10 . Иллюстрация двух проектируемых универсальных дистрибутивов HTC. HTC-корреляция может рассматриваться как форма модели пониженного порядка. В области теплопередачи корреляции HTC обычно выражаются в безразмерной форме, чтобы явно выявить определяющие физические параметры. Хотя безразмерные корреляции широко используются в академических кругах, они не совсем понятны для операций литья.На практике HTC выражается в размерных формах и является функцией измеряемых рабочих параметров. Настоящее исследование следует этому соглашению, и все корреляции выражены в размерных формах. HTC — это локализованный параметр, и его значение изменяется как в направлении заброса, так и в поперечном направлении, как показано на рисунке 9B. Однако, если предположить, что распределения HTC из разных рабочих условий удовлетворяют одной и той же нормализованной универсальной функции распределения в одном и том же направлении, распределение HTC при любых заданных рабочих условиях может быть восстановлено на основе двух универсальных функций распределения, определенных в уравнениях 31 и 32 и характеристика HTC, зависящая от рабочего состояния.Такая характеристика HTC не зависит от специальных координат и представляет собой единственное сосредоточенное значение для определенного состояния. В текущем исследовании в качестве характеристического значения используется максимальное значение HTC в профиле HTC. Корреляцию между характеристикой HTC и восемью рабочими параметрами можно получить либо с помощью линейного регрессионного анализа, либо с помощью аппроксимации кривой. Однако окончательная форма корреляции должна быть математически простой, в противном случае потребуется значительное количество вычислительного времени, что приведет к задержке управления литьем.Самая прямая корреляция — это предположить, что характеристика HTC, или сосредоточенная HTC, является явной линейной функцией рабочих параметров: Коэффициенты в уравнении. 33 можно найти с помощью многомерного линейного регрессионного анализа. В текущем исследовании использовался OriginLab® для получения коэффициентов, и окончательная форма многомерной корреляции на основе линейной регрессии показана следующим образом: В качестве альтернативы, математически удобно объединить все восемь рабочих параметров в одну переменную и преобразовать многомерный линейный регрессионный анализ в линейный регрессионный анализ с одной переменной. Объединенную одиночную переменную можно записать следующим образом: Коэффициенты в уравнении.35 не определены однозначно. Их можно рассматривать как вес каждого рабочего параметра и их можно калибровать для разных разливочных машин. Коэффициенты, применяемые в данном исследовании, основаны на разливочной машине промышленного партнера, а калиброванная единственная переменная имеет следующий вид: Комбинированная переменная χ коррелирует с сосредоточенным значением HTC посредством анализа линейной регрессии и аппроксимации экспоненциальной кривой в текущем исследовании.Две корреляции показаны следующим образом: Рисунок 11 показывает сравнение между HTC, предсказанными CFD, и HTC, предсказанными корреляцией. Многопараметрическая линейная корреляция имеет тенденцию переоценивать теплопередачу при более низких значениях HTC, но недооценивать распылительное охлаждение при более высоких значениях. Экспоненциальная корреляция также показывает похожие тенденции. Прогнозы на основе линейной корреляции одной переменной более точны, чем два других при более низких значениях HTC, тогда прогнозы становятся колеблющимися между завышенными и заниженными при больших значениях HTC.В целом, многомерная линейная корреляция лучше всего подходит для всех трех корреляций с точки зрения точности. Кроме того, он включает только две основные математические операции, то есть умножение и сложение. Такие функции должны обеспечивать быстрое предсказание, тем самым позволяя управлять кастингом в реальном времени. Однако две другие корреляции все же можно рассматривать как потенциальные кандидаты. При тщательной калибровке объединенной единственной переменной более сложные математические операции в этих двух корреляциях могут лучше выявить взаимосвязанный характер между рабочими параметрами литья. РИСУНОК 11 . Сравнение HTC, предсказанных с помощью CFD, и HTC, предсказанных корреляцией. Локализованное распределение HTC реконструируется во время приложения. Процесс реконструкции состоит из трех этапов: определение покрытия HTC, вычисление сосредоточенного HTC и создание распределения HTC. Покрытие HTC исключено из функций универсального распределения, но его следует учитывать на этапе реконструкции.Для любых условий эксплуатации покрытие HTC на стальной поверхности может быть рассчитано на основе расстояния зазора, угла распыления (в плоскости, перпендикулярной направлению разливки) и угла распространения (в плоскости, перпендикулярной поперечному направлению). ), как показано на рисунках 12A, B. Границы покрытия HTC, как показано на рисунке 12C, могут быть найдены из тригонометрических соотношений и определены следующим образом: РИСУНОК 12 .Расчет HTC покрытия на стальной поверхности (A) направление литья , (B) поперечное направление и (C) вид сверху шаблона HTC. Сосредоточенное HTC рассчитывается на основе уравнения. 34 с восемью предопределенными рабочими параметрами. Наконец, локальное значение HTC в любой заданной точке (Xi, Yj) в пределах покрытия HTC может быть вычислено на основе уравнений 27, 29, 31 и 32: Повторяя вышеупомянутый процесс с заданными пользователем приращениями в обоих направлениях, создается двумерное распределение HTC.На рисунке 13 показано сравнение распределения HTC, предсказанного с помощью CFD, и распределения HTC, предсказанного корреляцией. Распределение HTC, полученное при моделировании CFD, имеет случайные всплески по охвату по сравнению с плавным распределением, предсказанным с помощью корреляции. Это связано с тем, что высокоточное моделирование CFD способно уловить подробные явления во время теплопередачи при ударе капли от стали, такие как отражение капли и скользящая капля по поверхности стали. Реконструированное распределение HTC низкого порядка исключает некоторые из этих подробных локальных эффектов для повышения вычислительной эффективности. РИСУНОК 13 . Сравнение распределений HTC (A), предсказано CFD, и (B), предсказано корреляцией. Корреляция вместе с процедурой реконструкции, разработанной в текущем исследовании, может быть запрограммирована в новых системах управления литьем как подпрограмма. В качестве альтернативы, графический интерфейс был создан как дополнительный компонент для существующих систем управления. На рисунке 14 показан интерфейс бета-версии. Интерфейс иллюстрирует определение покрытия HTC, чтобы устранить путаницу и двусмысленность.Кнопки ввода позволяют пользователям вводить значения восьми рабочих параметров и приращения в двух направлениях. Скрытое окно по запросу содержит подробное определение каждого входного параметра. Программа запускается, когда пользователи нажимают кнопку «Создать», и создает электронную таблицу в универсальном формате значений, разделенных запятыми (csv), который включает в себя специальные координаты и соответствующие локальные значения HTC в пределах зоны действия HTC. Таблицу можно удобно импортировать в существующую систему управления в качестве граничного условия для расчета затвердевания.В будущих версиях графического интерфейса пользователя HTC основное внимание будет уделяться созданию массивных прогнозов HTC, позволяя пользователям импортировать матрицу рабочих условий вместо того, чтобы вводить числа вручную. РИСУНОК 14 . Графический интерфейс пользователя HTC-корреляции. 5 Вышеупомянутые корреляции HTC вместе с графическим интерфейсом должны принести пользу сталелитейной промышленности по крайней мере в следующих аспектах: 1) ускорение процесса разработки корреляций HTC для новых конфигураций форсунок и условий эксплуатации.Например, технология охлаждения распылением постоянно развивается по мере того, как форсунки производят передовые конструкции распылительных форсунок. В корреляциях HTC необходимо учитывать новые характеристики распыления, то есть более мелкие капли воды, меньшую длину разрыва жидкого слоя, многофазное распыление и т. Д. Текущий численный подход должен значительно сократить время на разработку новых корреляций при изменении характеристик распыления. Кроме того, постоянно растет спрос на новые виды металлопродукции.Для каждого типа стали требуется особая стратегия охлаждения распылением, включая тип форсунки (гидравлическое или воздушно-распылительное), расположение форсунок и интенсивность распыления (скорость потока распыления и расстояние зазора). Текущий высокопроизводительный численный компьютерный метод будет полезен для своевременной разработки новой стратегии охлаждения. 2) реализация динамического управления охлаждением распылением на месте в реальном времени. Одной из основных целей разработки корреляций HTC является обеспечение контроля в реальном времени во время непрерывного литья. Корреляции HTC, предложенные в этом исследовании, и удобный интерфейс позволят мгновенно генерировать значения HTC как в направлении заброса, так и в поперечном направлении.Когда этот процесс прогнозирования автоматизирован и интегрирован с модулем прогнозирования затвердевания и модулем управления, процесс прогнозирования и динамического управления может выполняться практически в реальном времени. 3) поддержка выбора распылительной форсунки на этапе проектирования литейщика. Текущий графический интерфейс HTC был разработан как для автономных, так и для интерактивных приложений. При автономном применении графический пользовательский интерфейс HTC может использоваться для сценариев «что, если» и предоставлять значения HTC для различных расположений сопел и условий эксплуатации. Инженеры могут выбрать оптимальный тип форсунки и стратегию охлаждения для конкретного литейщика на основе прогнозируемых значений HTC.4) Устранение неисправностей форсунок. Предыдущие корреляции HTC были разработаны на основе идеальных условий эксплуатации. Таким образом, их можно использовать для идентификации форсунок, отклоняющихся от проектных условий. Например, засорение форсунок из-за отложений включений будет давать различную форму распыления на поверхности плиты, следовательно, создавать другой профиль охлаждения. Оператор может сравнить прогнозируемый температурный профиль с измеренным и определить неисправное сопло, где разница температур велика (за пределами допуска). Эффективный отвод тепла без ущерба для прочности и качества стали во время вторичного охлаждения требует точного контроля литья и динамической регулировки расхода распыляемой воды. На практике HTC на стальной поверхности был принят в качестве индикатора для количественной оценки скорости охлаждения распылением, а также служил одним из критических граничных условий для расчета затвердевания. Корреляции HTC, основанные на экспериментах, широко используются в отрасли для прогнозирования значений HTC в различных условиях эксплуатации, но процесс разработки является трудоемким и может охватывать только ограниченный диапазон рабочих условий. В качестве альтернативы текущее исследование предлагает численный подход для эффективного создания корреляций HTC за относительно короткий период времени. Численный подход состоит из этапа численного моделирования, этапа анализа данных и этапа разработки графического интерфейса пользователя. Трехмерная CFD-модель с высокой точностью, разработанная на этапе численного моделирования, включает моделирование наиболее важных физических процессов в процессе вторичного охлаждения, таких как распыление, дробление капель, столкновение капель, захват воздуха, теплопередача при ударе капли о сталь и сталь. охлаждение.База данных HTC была создана на этапе моделирования с помощью высокопроизводительных параллельных вычислений. На этапе анализа данных распределения различных профилей HTC на стальной поверхности были разложены на две нормированные универсальные функции распределения. С другой стороны, величина HTC в зоне действия HTC была объединена в характеристическое значение, которое коррелировалось с восемью репрезентативными рабочими параметрами посредством регрессионного анализа и подбора кривой. Многопараметрическая линейная корреляция лучше всего подходит для всех трех корреляций, и она была интегрирована в удобный графический интерфейс.Посредством реконструкции HTC графический интерфейс пользователя генерирует электронную таблицу, содержащую подробные локальные значения HTC на основе данных, вводимых пользователем. Таблицу можно включить в существующую систему управления в качестве граничного условия для расчета затвердевания. Численная методология должна принести пользу сталелитейной промышленности, ускорив процесс разработки корреляций HTC, обеспечив управление динамическим охлаждением распылением в реальном времени, поддерживая выбор сопел, устраняя неисправности сопел, а также способствуя дальнейшему повышению точности существующих систем управления литьем. Исходные материалы, представленные в исследовании, включены в статьи / дополнительные материалы, дальнейшие запросы можно направлять соответствующим авторам. HM провел моделирование CFD, проанализировал данные и написал рукопись. А.С. контролировал процесс исследования, давал рекомендации по моделированию CFD, а также рецензировал и редактировал рукопись. CZ получил финансирование для текущего исследования, концептуализировал методологию, руководил процессом исследования, а также рассмотрел и отредактировал рукопись. Эта работа финансировалась Консорциумом моделирования и визуализации производства стали (SMSVC). Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. Авторы хотели бы поблагодарить Центр инноваций через визуализацию и моделирование (CIVS) в Университете Пердью Северо-Запад за предоставление всех ресурсов, необходимых для этой работы.Авторы также хотели бы выразить особую благодарность доктору Руи Лю за его руководство и поддержку. Вторая эффективная площадь контакта капли с плитой, м 2 Акао, Ф., Араки, К., Мори, С., и Морияма, А. (1980). Деформационное поведение капли жидкости, падающей на поверхность горячего металла. Пер. ISIJ 20 (11), 737–743. doi: 10.2355 / isijinternational1966.20.737 CrossRef Полный текст | Google Scholar Бернардин Дж. Д. и Мудавар И. (1999). Точка Лейденфроста: экспериментальное изучение и оценка существующих моделей. J. Heat Tran. 121 (4), 894–903. doi: 10.1115 / 1.2826080 CrossRef Полный текст | Google Scholar Биркхольд, Ф. (2007). Селективное каталитическое восстановление оксидов азота в автомобилях: исследование закачки водного раствора мочевины.Кандидатская диссертация. Карлсруэ (Германия): Университет Карлсруэ. Google Scholar Blazek, K., Moravec, R., Zheng, K., Lowry, M., and Yin, H. (2013). «Динамическое моделирование поведения центральной линии слябов в процессе непрерывной разливки при больших изменениях скорости и их влияние на внутреннее качество слябов», в материалах 5-й международной конференции по моделированию и моделированию металлургических процессов в сталеплавильном производстве, Острава, Чешская Республика, 10–12 сентября. , 2013 (Warrendale, PA: Association for Iron & Steel Technology). Google Scholar Болле, Л., и Муро, Дж. (2016). Теория и применение для распылительного охлаждения горячих поверхностей. Мульт. Scien. Техн. 28 (4), 321–417. doi: 10.1615 / MultScienTechn.v28.i4.10 CrossRef Полный текст | Google Scholar Бримакомб, Дж. К., Агарвал, П. К., Баптиста, Л. А., Хиббинс, С., и Прабхакар, Б. (1980). Распылительное охлаждение при непрерывной разливке стали. Непрерывное литье 2, 109–123. Google Scholar Данциг, Дж.А., Раппаз М. (2016). Затвердевание . 2-е изд. Лозанна, Швейцария: EPFL press. Google Scholar Домбровски Н. и Хупер П. К. (1962). Влияние плотности окружающей среды на образование капель в аэрозольных баллончиках. Chem. Англ. Sci. 17 (4), 291–305. doi: 10.1016 / 0009-2509 (62) 85008-8 CrossRef Полный текст | Google Scholar Fung, M.C., Inthavong, K., Yang, W., and Tu, J. (2012). CFD-моделирование распыления распылителя для носового распылителя. Аэрозоль. Sci. Technol. 46 (11), 1219–1226. doi: 10.1080 / 02786826.2012.704098 CrossRef Полный текст | Google Scholar Госман, А. Д., и Йоенидес, Э. (1983). Аспекты компьютерного моделирования жидкостных топок. J. Energy 7 (6), 482–490. doi: 10.2514 / 3.62687 CrossRef Полный текст | Google Scholar Hardin, R.A., and Beckermann, C. (2018). Моделирование теплопередачи и затвердевания непрерывной разливки стальных слябов. Материалы конференции и выставки технологий чугуна и стали AISTech 2018, Миссури, США, 4–7 мая 2009 г. (Warrendale, PA: Association for Iron and Steel Technology). Google Scholar Хардин Р. А., Лю К., Бекерманн К. и Капур А. (2003). Моделирование переходных процессов и модель управления динамическим охлаждением распылением для непрерывной разливки стали. Металл. Матер. Пер. В 34 (3), 297–306. doi: 10.1007 / s11663-003-0075-0 CrossRef Полный текст | Google Scholar Hardin, R.A., Shen, H., and Beckermann, C. (2000). Моделирование теплопередачи машины непрерывной разливки стальных слябов с использованием реалистичных схем распыления. Труды моделирования процессов литья, сварки и глубокой кристаллизации IX .Варрендейл, Пенсильвания: Минералы, металлы и материалы Общества. 729–736. Google Scholar Хорски Дж., Рауденский М. и Ценг А. А. (2005). «Исследование теплопередачи вторичного охлаждения при непрерывной разливке», в материалах конференции и выставки по технологиям чугуна и стали AISTech, Шарлотт, Северная Каролина, США, 912 мая 2005 г. (Варрендейл, Пенсильвания: Ассоциация технологий чугуна и стали). Google Scholar Исса, Р. Дж. (2004). Численное моделирование динамики и теплопередачи ударных распылителей в широком диапазоне давлений.Докторская диссертация. Питтсбург (Пенсильвания): Университет Питтсбурга, URI. Google Scholar Корич С. и Томас Б. Г. (2006). Эффективная термомеханическая модель процессов затвердевания. Внутр. J. Numer. Методы англ. 66, 1955–1989. doi: 10.1002 / nme.1614 CrossRef Полный текст | Google Scholar Laitinen, E., and Neittaanmäki, P. (1988). О численном моделировании процесса непрерывной разливки. J. Eng. Математика. 22 (4), 335–354.doi: 10.1007 / BF00058513 CrossRef Полный текст | Google Scholar Лю А. Б., Мазер Д. и Райтц Р. Д. (1993). Моделирование эффектов перетаскивания и разрушения капли на брызгах топлива. J. Двигатели 102 (3), 83–95. doi: 10.4271 / Теплопередача стальных капель
Расчет коэффициента теплопередачи
Расчетная область и граничные условия
Рабочие условия
Проверка
Размер капли
Ударная теплопередача
Результаты и обсуждения
Распределение коэффициента теплопередачи на стальной поверхности
Корреляция коэффициентов теплопередачи
Реконструкция коэффициента теплопередачи и графический интерфейс
Возможные приложения
Заключение
Заявление о доступности данных
Вклад авторов
Финансирование
Конфликт интересов
Благодарности
Глоссарий
Ai коэффициент корреляции многомерной линейной регрессии, i изменяется от 0 до 8
ai показатель степени независимой переменной, i изменяется от единицы до 8
B0 капля константа размера, которая в данном исследовании установлена равной 0,61
Постоянная времени разрушения B1
bcrit критическое смещение, m
bi коэффициент независимой переменной, i варьируется от единицы до 8
boffset смещение центра большей капли и траектории движения капля меньшего размера, m
CD Коэффициент лобового сопротивления
Постоянная связки CL, равная 0.5 в данном исследовании
Cs концентрация пара на поверхности капли, кмоль / м 3
C∞ концентрация пара в объемном потоке, кмоль / м 3
cp удельная теплоемкость капли, Дж / кг · K
D Расстояние между соплом и соплом, мм
Расстояние Drow между соседними рядами распылителей, мм
D Коэффициент диффузии пара в воздухе, м 2 / с
d Диаметр капли, м
do диаметр разрыва капли от связок, м
eff эффективность теплоотдачи
g ускорение свободного падения, м / с 2
Hπ высота листа при Ψ = π, м
HTC коэффициент теплопередачи за счет распылительного охлаждения, Вт / м 2 · K
HTC местное тепло коэффициент теплоотдачи за счет распылительного охлаждения, Вт / м 2 · K
HTCl Суммированный коэффициент теплопередачи за счет распылительного охлаждения, Вт / м 2 · K
HTCnorm-x, i нормированный коэффициент теплоотдачи i-й точки в направлении x , Вт / м 2 · K
HTCnorm-y, j нормализованная теплопередача Коэффициент nsfer j-й точки в направлении y, Вт / м 2 · K
H Расстояние отрыва распылителя, мм
h Коэффициент конвективной теплоотдачи, Вт / м 2 · K
hfg Скрытая теплота капли, Дж / кг
iith точка в распределении HTC
jj-я точка в распределении HTC
Ks волновое число, соответствующее максимальной скорости роста Ω
k кинетическая энергия турбулентности, м 2 / с 2
kair Теплопроводность воздуха, Вт / м · K
kc коэффициент массопереноса, м / с
kdrop теплопроводность капли, Вт / мK
Lb длина пленки, в которой она разрывается на связки, м
ln (ηb / ηo) эмпирическая константа слоя, которая устанавливается равной 12 в этом исследовании (Weber, 1931; Dombrowski and Hooper, 1962)
м общее количество точек в направлении y в пределах распределения HTC
mdrop масса отдельной капли, кг
Nudrop Nusselt число капли
n общее количество точек в направлении x в пределах распределения HTC
n2 число столкновений между более крупной каплей и другими более мелкими каплями
Oh Число Онезорге
P случайное число от 0 до 1
Pr Число Прандтля
P (n) вероятность столкновения
Q Поток воды при распылении воды, л / м 2 · с
qsec ″ тепловой поток за счет теплопроводности, Вт / м 2
qconv ″ тепловой поток за счет конвекции, Вт / м 2
qR ″ тепловой поток через излучение, Вт / м 2
qtotal ″ общий тепловой поток через стенки формы, Вт / м 2
Число Редропа Рейнольдса капли
r Радиус капли.Нижний индекс 1 соответствует большей капле до слияния, а меньшая капля обозначается цифрой 2. Нижний индекс «Дочерний» обозначает вновь образованные капли после распада, а «Родительский» обозначает каплю до распада, m
Sdrop-air external источник из-за взаимодействия капли с воздухом
Sc Номер Шмидта
Шдроп Номер Шервуда
sslab расстояние от центра капли до поверхности пластины, м
Sφ внутренний источник для непрерывной фазы
Tcell температура центроида ячейки, K температура центроида ячейки, K
T температура центроида ячейки, K температура центроида ячейки, K
T температура капельной капли, K
T температура грани центроида грани, K
TR температура излучения, (∫Ω = 4πIdΩ / 4σSB) 1/4, K.I — интенсивность излучения, Ω — телесный угол
T Температура распыляемой воды, K
T∞ Локальная температура непрерывной фазы, K
t время, с
t Время контакта капли между каплей и поверхностью плиты во время удара, с
U полная скорость жидкой пленки на выходе из инжектора, м / с
u скорость капли до слияния, более крупная капля передается с номером один, а меньшая капля идентифицируется с номером 2, м / с
u воздух воздух скорость, м / с
Скорость капли, м / с
Скорость разливки Vcast, м / мин
Объем расчетной ячейки Vcell, м 3
Координата Xix i-й точки в распределении HTC, м
Xnorm, i нормированная координата x точки i относительно ее минимального и максимального значений
Yjy координата j-й точки в распределении HTC, м
Ynorm, j нормализованная координата y j-й точки относительно ее минимального и максимального значений
y + безразмерное расстояние до стены 918 45 αcal зависящий от машины калибровочный коэффициент, рекомендуется типичное значение, равное четырем
β константа, определяемая из сохранения массы и импульса
Δy расстояние от центроида твердого тела до центроида грани, м
ε скорость рассеяния турбулентности, м 2 / s 3
ε коэффициент излучения капли
η направление распыления, число 1, 0.925 и 0,85 обозначены для верхнего распыления, бокового распыления и нижнего распыления, соответственно
θ угол распыления, градус
θ угол распространения, градус
Λ соответствующая длина волны для максимальной скорости роста, м
λ теплопроводность стали стали, Вт / м · К
Вязкость микрокапли, Н · с / м 2
ρплотность воздуха, кг / м 3
ρкапельная плотность капли, кг / м 3
σ поверхностное натяжение между водой и воздухом , Н / м
σSB постоянная Стефана-Больцмана, 5.67×10 –8 Вт / м 2 · K 4
ϕ угол падения в вертикальной плоскости
φ универсальная переменная
χ комбинированная одиночная переменная для корреляции HTC
Ψ угол падения в горизонтальной плоскости
Ом максимальная скорость роста спектра бесконечно малых волновых возмущений
ω удельная скорость диссипации турбулентности, 1 / с Литература
CrossRef Полный текст | Google Scholar
Лю, Х., Цай, К., Янь, Ю., Цзя, М., и Инь, Б. (2018). Численное моделирование и экспериментальное исследование распылительного охлаждения в некипящей области. Heat Mass Tran. 54, 3747–3760.doi: 10.1007 / s00231-018-2402-7
CrossRef Полный текст | Google Scholar
Long, M., Chen, H., Chen, D., Yu, S., Liang, B., and Duan, H. (2018). Комбинированная гибридная 3-D / 2-D модель для прогнозирования течения и затвердевания во время непрерывной разливки слябов. Металлы 8 (3), 182. doi: 10.3390 / met8030182
CrossRef Полный текст | Google Scholar
Менг, Ю.А., и Томас, Б.Г. (2003). Модель теплопередачи и затвердевания непрерывной разливки слябов: CON1D. Металл.Матер. Пер. В 34 (5), 685–705. doi: 10.1007 / s11663-003-0040-y
CrossRef Полный текст | Google Scholar
Ментер, Ф. Р. (1993). «Модели турбулентности с двумя зональными уравнениями k-ω для аэродинамических потоков», в материалах 24-й конференции по гидродинамике AIAA, Орландо, Флорида, 69 июля 1993 г. (Рестон, Вирджиния: Американский институт аэронавтики и астронавтики).
Google Scholar
Моралес Р. Д., Лопес А. Г. и Оливарес И. М. (1990). Анализ теплопередачи при водяном охлаждении стальных стержней. ISIJ Int. 30 (1), 48–57. doi: 10.2355 / isijinternational.30.48
CrossRef Полный текст | Google Scholar
Mosayebidorcheh, S., and Gorji-Bandpy, M. (2017). Анализ затвердевания и тепловых характеристик низкоуглеродистой стали в процессе непрерывной разливки. J. Adv. Матер. Процесс. 5 (3), 3–11.
Google Scholar
Mundo, C., Tropea, C., and Sommerfeld, M. (1997). Численное и экспериментальное исследование характеристик струи в окрестности жесткой стенки. Exp. Therm. Fluid Sci. 15 (3), 228–237. doi: 10.1016 / S0894-1777 (97) 00015-0
CrossRef Полный текст | Google Scholar
Naber, J. D., and Reitz, R. D. (1988). Моделирование брызг двигателя / столкновения со стеной. J. Двигатели 97 (6), 118–140.
Google Scholar
Нидждам, Дж. Дж., Гуо, Б., Флетчер, Д. Ф., и Лэнгриш, Т. А. (2006). Лагранжевые и эйлеровы модели для моделирования турбулентного рассеивания и слияния капель внутри спрея. Заявл.Математика. Модель. 30 (11), 1196–1211. doi: 10.1016 / j.apm.2006.02.001
CrossRef Полный текст | Google Scholar
Nozaki, T., Matsuno, J.-i., Murata, K., Ooi, H., and Kodama, M. (1978). Схема вторичного охлаждения для предотвращения поверхностных трещин в слябах для непрерывной разливки. ISIJ Int. 18 (6), 330–338. doi: 10.2355 / isijinternational1966.18.330
CrossRef Полный текст | Google Scholar
О’Рурк, П. Дж. (1981). Коллективное воздействие капель на струи испаряющейся жидкости .Кандидатская диссертация. Принстон (Нью-Джерси): Принстонский университет.
Google Scholar
Онезорге, В. (1936). Die bildung von tropfen an düsen und die auflösung flüssiger strahlen. Z. Angew. Математика. Мех. 16 (6), 355–358. doi: 10.1002 / zamm.19360160611
CrossRef Полный текст | Google Scholar
Ранц В. Э. и Маршалл В. Р. (1952). Испарение из капель. Chem. Англ. Прог. 48 (3), 141–146.
Google Scholar
Reitz, R.D.(1978). Распыление и другие режимы разрушения струи жидкости. Кандидатская диссертация. Принстон (Нью-Джерси): Принстонский университет.
Google Scholar
Рейц, Р. Д. (1987). Моделирование процессов распыления в распыляющих распылителях высокого давления. At. Spray Tech. 3 (4), 309–337.
Google Scholar
Сенекал, П. К., Шмидт, Д. П., Нуар, И., Ратленд, К. Дж., Райтц, Р. Д., и Коррадини, М. Л. (1999). Моделирование высокоскоростного распыления листа вязкой жидкостью. Внутр. J. Multiphas.Flow 25 (6-7), 10731097. doi: 10.1016 / S0301-9322 (99) 00057-9
CrossRef Полный текст | Google Scholar
Сенгупта, Дж., Томас, Б. Г., и Уэллс, М. А. (2005). Использование водяного охлаждения при непрерывной разливке стали и алюминиевых сплавов. Металл. Матер. Пер. 36 (1), 187–204. doi: 10.1007 / s11661-005-0151-y
CrossRef Полный текст | Google Scholar
Tang, L., Yao, M., Wang, X., and Zhang, X. (2012). Неравномерные термические свойства и рост оболочки внутри кристаллизатора для непрерывной разливки широких и толстых слябов. Steel Research Int. 83 (12), 1203–1213. doi: 10.1002 / srin.201200075
CrossRef Полный текст | Google Scholar
Thomas, B.G., и Ho, B. (1996). Листовая модель непрерывного литья. J. Manuf. Sci. Англ. 118 (1), 37–44. doi: 10.1115 / 1.2803646
CrossRef Полный текст | Google Scholar
Weber, C. (1931). Zum Zerfall eines Flüssigkeitsstrahles. Z. Angew. Математика. Мех. 11 (2), 136–154. doi: 10.1002 / zamm.1
10207
CrossRef Полный текст | Google Scholar
Zuckerman, N., и Лиор, Н. (2006). Теплообмен при ударе струи: физика, корреляции, численное моделирование. Adv. Heat Tran. 39, 565–631. doi: 10.1016 / S0065-2717 (06) 39006-5
CrossRef Полный текст | Google Scholar
Коэффициент теплопередачи повторно используемого бетонного кирпича в сочетании со стеной из изоляционной плиты EPS
Четыре образца тектонических форм были взяты для проверки их коэффициентов теплопередачи. Путем анализа и сравнения тестовых значений и теоретических значений коэффициента теплопередачи был предложен метод расчета скорректированного значения для определения коэффициента теплопередачи; Предложенный метод оказался достаточно корректным.Результаты показали, что коэффициент теплопередачи кирпичной стены из вторичного бетона выше, чем у стены из глиняного кирпича, коэффициент теплопередачи кирпичной стены из вторичного бетона может быть эффективно снижен в сочетании с изоляционной панелью из пенополистирола, а тип теплоизоляции сэндвич был лучше. чем у типа внешней теплоизоляции.
1. Введение
По мере того, как урбанизация постепенно расширяется, также увеличиваются быстрые темпы строительства зданий и выдающиеся достижения в области энергосбережения [1].Энергосбережение играет важную роль в национальных энергетических стратегиях, снижая значительную нагрузку на ресурсы и окружающую среду [2, 3]. В элементах частокола здания площадь внешней стены занимает большую долю по сравнению с крышей здания, дверями, окнами и т. Д. [4, 5]. Тепловая консервация наружных стен является ключом к достижению энергоэффективности в зданиях [5, 6]. Наружные стены различаются в зависимости от строительных материалов, типов конструкций и условий окружающей среды.Глиняный кирпич, который широко используется во многих существующих зданиях, нанес большой ущерб земельным ресурсам. Производственный процесс с использованием высокотемпературной печи также привел к увеличению выбросов парниковых газов. Таким образом, возникла растущая потребность в исследованиях строительных материалов для зеленых стен и их термоконсервации и теплоизоляционных характеристик. Переработанный бетонный кирпич, изготовленный из измельченных отходов бетона, широко используется в кирпичных конструкциях в качестве экологически чистых строительных материалов.Было проведено множество исследований его механических свойств, но лишь несколько измерений его теплоизоляционных свойств [7]. Кроме того, наиболее распространенным типом теплоизоляции было добавление теплосохраняющих материалов на внешней стороне внешней стены, с самым большим ограничением, заключающимся в более коротком сроке службы [8, 9]. Вспениваемый полистирол (EPS), используемый для теплоизоляции, продемонстрировал очевидные характеристики сохранения тепла и теплоизоляции. Тем не менее, различные материалы для наружных стен с различными формами структурных типов для сохранения тепла из пенополистирола, независимо от того, сильно ли отличаются вариации их теплоизоляционных свойств, традиционно не были в центре внимания в контексте сохранения тепла стен и энергосбережения.
Коэффициент теплопередачи () обычно использовался в качестве показателя для измерения термоконсервации и изоляционных характеристик стены корпуса и в основном определялся коэффициентом теплопроводности () материалов. Считается, что тепловая и влажная среда влияет на характеристики теплопередачи стенок корпуса [10–12]. Коэффициент теплопроводности изменялся в зависимости от температуры и влажности воздуха, что приводило к отклонению между фактическим и теоретическим значением.Однако во многих исследованиях предполагалось, что характеристики материала не будут изменены или коэффициент теплопроводности () материалов выражен как постоянный. Следовательно, существует растущая потребность в изучении скорректированного коэффициента теплопроводности материала в различных средах и его расширенном применении в энергосберегающих конструкциях.
Переработанный бетонный кирпич имеет все больший потенциал развития и использования. Его различная комбинация с изоляционной плитой EPS имеет как эффект экологической защиты окружающей среды, так и энергосбережение.Понимание характеристик теплопередачи вторичного бетонного кирпича в сочетании с изоляционной плитой из пенополистирола становится все более необходимым для количественной оценки их вклада в энергосбережение.
Целями данного исследования было испытание коэффициента теплопередачи () кирпичной стены из вторичного бетона, прямое сравнение теплового поведения различных строительных решений стен и предложение скорректированного метода расчета коэффициента теплопередачи при оптимизации энергопотребления здания. .
2. Тест коэффициента теплопередачи
В настоящее время не существует официального стандарта для методов испытаний, которые непосредственно касаются динамических характеристик стен: основные справочные нормы [13] включают измерение стационарных характеристик одинарных материалов и многослойных конструкций. при стандартных граничных условиях. В этом исследовании был проведен экспериментальный анализ климатической камеры для сравнения влияния коэффициента теплопередачи элементов оболочки, которые характеризуются эквивалентными характеристиками в установившемся режиме.
2.1. Типы стен и свойства материалов
В этом исследовании были изготовлены четыре различных образца для количественной оценки их тепловых характеристик. Четыре образца, выбранные из типологии стен, подробно описаны на Рисунке 1 и в Таблице 1.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2. Прибор для испытаний
В соответствии со стандартами и исследованиями, касающимися этого типа испытаний [14, 15], в экспериментальном исследовании использовался прибор для измерения стационарной теплопередачи (CD-WTFl515, Шэньян, Китай).Условия теплопередачи тестируемой оболочки здания моделируются на основе стандарта GB / T 13475-2008 и однонаправленного устойчивого принципа теплопередачи для измерения и анализа коэффициента теплопередачи. Климатическая установка с контролем окружающей среды состоит из двух камер с кондиционированием воздуха, в которых температура регулируется с помощью термостойких проводов и систем охлаждения (рисунки 2 и 3). Одна камера используется для создания микроклимата на открытом воздухе. Температура дозирующего резервуара установлена на -10 ° C (при допустимом перепаде температур ± 0.2 ° С). Другая камера имитирует внутреннюю среду, в которой температура установлена на 35 ° C (с допустимой разностью температур ± 0,1 ° C). Образцы были изготовлены в соответствии с предусмотренными размерами испытательного оборудования. Размеры установки и образцов составляют 2600 × 2160 × 2140 мм в высоту и 1500 × (≤400) × 1500 мм соответственно (рисунок 4). После 28 дней естественной сушки в испытательном устройстве поверхность раздела между образцами и испытательным устройством была герметизирована пенополиуретаном.
Все образцы были протестированы в Пекинском центре испытаний строительных материалов. Перед обработкой образцов стен в аппарате сначала была проведена калибровка установки. Образцы стен внутри и снаружи должны соответствовать горячей и холодной камерам соответственно. Для каждого образца были измерены шесть групп данных связанных параметров окружающей среды, таких как температура горячего поля () и холодного поля (), влажность горячего поля () и холодного поля (), а также общая входная мощность (). уменьшить погрешность измерения.С каждой стороны образцов симметрично подключалось по девять датчиков температуры. Допустимый перепад температуры поверхности образца составлял ± 0,5 ° C, с интервалом сбора данных 10 мин. Измерения проводились на основе настроек параметров в соответствии с положениями стандарта GB / T 13475-2008. Когда допустимый перепад температур был в пределах диапазона значений после трех часов непрерывного климат-контроля, испытания были прекращены.
3. Расчет коэффициента теплопередачи Модель
Теплопередача через стену проходила в трех фазах: теплообмен внутренней поверхности; теплопроводность внутренней стены; теплообмен внешней поверхности.Методы расчета теплопередачи на каждом этапе различны [17], с точки зрения решения процесса уравнения Фурье с помощью метода испытаний и метода теории, граничных условий.
3.1. Принципы расчета тестовых значений
Принцип тестирования устройства для испытания теплопередачи в установившемся режиме (CD-WTFl515, Шэньян, Китай) основан на одномерном установившемся теплопереносе. Образцы были помещены между двумя различными температурными полями, чтобы моделировать теплопередачу стен в реальных условиях.По обе стороны от образца температура поверхности и температура воздуха измерялись датчиками температуры. Также были измерены поверхностные температуры с обеих сторон направляющей пластины. Были проверены внутренняя и внешняя температура поверхности измерительной коробки и входная мощность. По измеренным данным можно рассчитать коэффициент теплоотдачи стенок образцов [13], учтите, где — тепловой поток через стенку измерительной коробки (Вт · м −2 ), — коэффициент теплопередачи измерительной стенки (Вт м −2 K −1 ), является температурой внутренней поверхности измерительной камеры (K), и является температурой внешней поверхности измерительной камеры (K).
Тогда коэффициент теплопередачи конструкции ограждения можно рассчитать по следующей формуле: где — общая потребляемая мощность (Вт · м −2 ), — расчетная площадь измерения, — температура горячего поля (K), и — температура холодного поля (К).
3.2. Теоретическая расчетная модель
В условиях установившейся теплопередачи, когда весь процесс теплопередачи не изменяет общее количество тепла, закон Фурье может быть выражен как где — теплопередача плотности теплового потока конструкции, — тепло Коэффициент передачи оболочки здания (Вт · м −2 K −1 ) — это сопротивление теплопередаче внутренней поверхности, равное 0.11 м 2 K Вт −1 , сопротивление теплопередаче внешней поверхности, которое составляет 0,04 м 2 K Вт −1 , сопротивление теплопередаче каждого материала (м 2 K W −1 ), представляет собой сопротивление теплопередаче оболочки здания, является толщиной материалов (м) и является коэффициентом теплопроводности каждого материала (Вт · м −1 K −1 ).
3.3. Модель расчета скорректированного значения
Коэффициент теплопроводности материала является постоянным в существующих теоретических расчетах и численных расчетах, приведенных в литературе, без учета коэффициента теплопроводности материала при изменении температуры и влажности.Мы должны изучить истинное значение расчета коэффициента теплопередачи и применить его к теоретическому расчету.
3.3.1. Расчет коэффициента теплопроводности в реальных условиях эксплуатации
Механизм теплопередачи строительных материалов стен аналогичен жидкостному, который основан на упругих волнах. Теплопроводность увеличивалась с повышением температуры, а также на нее влияла влажность. Общее уравнение в случае реальных рабочих условий обычно выражается следующим образом: где — испытательное значение теплопроводности материала, — изменение теплопроводности, вызванное температурой, — изменение теплопроводности, вызванное влажностью веса, и — изменение теплопроводности. пробужденный от холода.
Были рассчитаны материалы, вызванные перепадом температуры, весом, влажностью и замерзанием, соответственно. Затем материалы были рассчитаны в рабочей среде на влияние теплопроводности на температуру и влажность.
Модель, используемая для описания влияния температуры и влажности на коэффициент теплопроводности неорганических вяжущих материалов, была [18]
Испытания на теплопроводность проводились на основе стандартов испытаний теплопроводности цементного раствора и кирпичей из вторичного бетона [16].Затем можно было рассчитать изменения теплопроводности материалов, вызванные температурой, весом, влажностью и замерзанием, соответственно. Коэффициенты теплопроводности () (относительное изменение при изменении на 0 ° C) цементного раствора и повторно используемых бетонных кирпичей были рассчитаны как 0,7526 Вт · м −1 K −1 и 0,6160 Вт · м −1 K −1. соответственно.
Влияние влажности на коэффициент теплопроводности шаблона EPS можно игнорировать [19]. Модель, используемая для описания влияния температуры на коэффициент теплопроводности шаблонов EPS, была [20] где — коэффициент теплопроводности неорганических связующих материалов при средней температуре, — коэффициент теплопроводности при 20 ° C, — коэффициент теплопроводности при 0 ° C. , — средняя температура материала, — коэффициент теплопроводности пенополистирола при 10 ° C, — коэффициент теплопроводности влаги, — влажность материала (%), — коэффициент с поправкой на влажность, — плотность материала (кг · м −3 ).
Когда стены демонстрируют явление конденсации, суточное количество конденсации может быть выражено как [17] где — суточное количество конденсации (г), — это парциальное давление водяного пара на стороне с более высоким парциальным давлением (), — водяной пар парциальное давление стороны с более низким парциальным давлением (), — сопротивление проницаемости водяного пара втекающего водяного пара (м 2 ч г −1 ), а также сопротивление проницаемости водяного пара вытекающего водяного пара (м 2 ч г −1 ).
3.3.2. Принципы расчета скорректированного значения
Теплопередача ограждающей конструкции здания обычно рассчитывалась на основе устойчивой теплопередачи с фиксированными значениями теплопроводности материалов. Тем не менее, теплопроводность при различных материалах оболочки здания и типах конструкций, независимо от того, отличаются ли эти изменения от постоянной теплопередачи в реальных рабочих условиях, традиционно не корректировалась в контексте исследований по энергосбережению.Следовательно, существует необходимость корректировать теплопроводность в зависимости от температуры и влажности. Расчет должен удовлетворять закону сохранения энергии, а плотность теплового потока через стену и каждый слой должна быть одинаковой. Рассмотрим где — тепловой поток, — тепловой поток на внутренней поверхности стенки (Вт · м −2 ), — тепловой поток на поверхности стенки (Вт · м −2 ), — тепловой поток через стенку (Вт · м −2 ), — это внутренний тепловой поток. температура поверхности любого слоя многослойной стены (K), температура воздуха в помещении (K), температура наружного воздуха (K) и сопротивление теплопередаче (м 2 K Вт −1 ).
Кроме того, расчет должен удовлетворять тому, что осмотическое количество не только пропорционально разнице давления пара между внутренним и внешним пространством, но также обратно пропорционально сопротивлению в процессе проникновения. Уравнение представлено как где — интенсивность инфильтрации водяного пара (г · м −2 · ч −1 ), — парциальное давление водяного пара воздуха в помещении (), — парциальное давление водяного пара наружного воздуха (), — полное сопротивление проникновению водяного пара из ограждающей конструкции (м 2 h g −1 ), сопротивление материалов проникновению водяного пара (m 2 h g −1 ), парциальное давление пара на внутренней поверхности любого слой многослойной стены ().
3.3.3. Правильный расчет коэффициента теплопередачи
В сочетании с этими известными значениями, такими как толщина материала каждой стены, теплопроводность и коэффициент проникновения водяного пара, распределение температуры внутри стены, распределение парциального давления водяного пара, содержание воды, и тогда можно было рассчитать количество льда. Это изменит теплопроводность каждого материала для расчета коэффициента теплопередачи. Затем модифицированные значения теплопроводности были повторно использованы для повторения расчета.Затем итеративно решается коэффициент теплопередачи до тех пор, пока изменение значений не будет соответствовать критерию сходимости (рисунок 5).
4. Результаты
4.1. Экспериментальные результаты и анализ неопределенностей
Средние значения соответствующих параметров окружающей среды для четырех образцов были показаны в таблице 2 соответственно. Неопределенность результатов измерения может быть связана с несколькими составляющими неопределенности. Суммарные стандартные неопределенности, вызванные повторяемостью измерений (), составили; ; ; , соответственно.Комбинированные стандартные неопределенности, вызванные ошибкой испытательного значения мощности () и ошибкой испытательного значения температуры (), составили 0,1% и 1%, в которых коэффициент охвата () равен 2. Таким образом, комбинированная стандартная неопределенность эксперимента с коэффициентом теплопередачи была синтезируются этими компонентами неопределенности [21]. Рассмотрим, какой коэффициент охвата () равен 2. Объединенные расширенные неопределенности для коэффициента теплопередачи составили 2,06%, 2,04%, 2,33% и 2,20% соответственно.


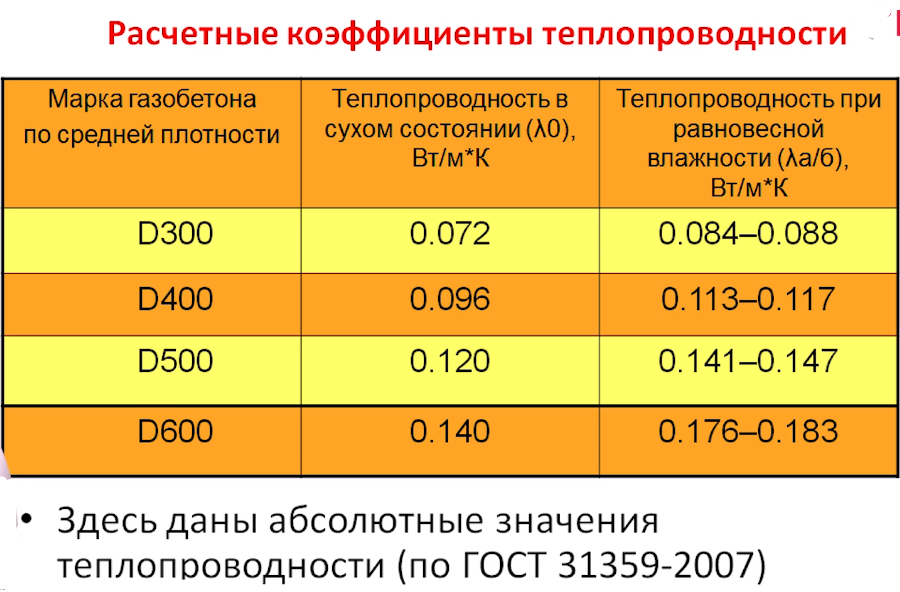 д.)
д.)